This article is about 4500 words long and is recommended for a reading time of over 10 minutes.
This article introduces Graphormer, a graph representation learning method based on the standard Transformer architecture.
1 Introduction
The Transformer architecture has shown excellent performance in fields such as natural language processing and computer vision, but it performs poorly in graph-level predictions. To address this issue, this article introduces Graphormer, a graph representation learning method based on the standard Transformer architecture, which has achieved outstanding results across a wide range of graph representation learning tasks, especially in the OGB large-scale challenge.
The key insight of Graphormer is to effectively encode the structural information of graphs into the model, for which several simple yet effective structural encoding methods are proposed. In addition, this article mathematically describes the expressive power of Graphormer and shows that many popular GNN variants can be considered as special cases of Graphormer.
2 Prerequisites
This section mainly reviews the prerequisites for Graph Neural Networks and Transformers:
Graph Neural Networks (GNN). GNNs learn representations of nodes and graphs by iteratively updating the representations of nodes, where the representation of a node is updated by aggregating the representations of its first or higher-order neighbors. The features aggregated in the l-th iteration can be represented by the AGGREGATE-COMBINE steps:
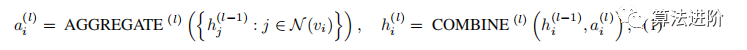
where N(vi) represents the set of first or higher-order neighbors of vi, the AGGREGATE function collects neighbor information, and common aggregation functions include MEAN, MAX, SUM, used for different architectures of GNNs, while the COMBINE function merges the neighbor information into the node representation.
Additionally, a READOUT function is designed to aggregate the final iterative node features into a representation for the entire graph, used for graph representation tasks.
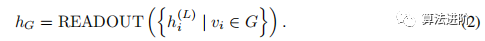
READOUT can be realized through simple permutation-invariant functions or more complex graph-level pooling functions.
Transformer. The Transformer architecture consists of Transformer layers, each including a self-attention module and a position feedforward network. The self-attention module projects the input H into Q, K, V, and then computes self-attention:
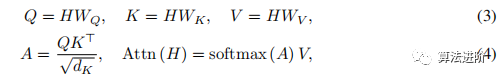
where the matrix A captures the similarity between queries and keys, simplified to single-head self-attention, assuming dK=dV=d, and omitting the bias term.
3 Graph Generator
This section introduces Graphormer for graph tasks, detailing the key designs in Graphormer, providing a detailed implementation of Graphormer, and demonstrating its superiority over popular GNN models.
3.1 Structural Encoding in Graphormer
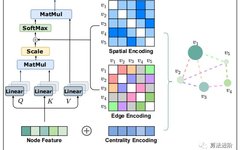
Graphormer introduces the structural information of graphs into the Transformer model through three simple yet effective encoding designs, as shown in Figure 1.
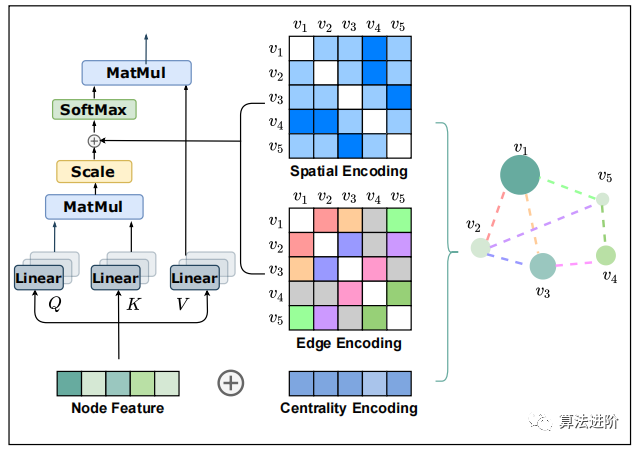
Figure 1 describes the key degree encoding, spatial encoding, and edge encoding proposed in our graph form (Graphormer).
3.1.1 Centrality Encoding
In Equation 4, the attention distribution is calculated based on the semantic relevance between nodes. However, node centrality (which measures the importance of a node in the graph) is often an important signal for graph understanding. For example, celebrities with a large number of followers are key factors in predicting trends in social networks [40,39]. This information is ignored in the current attention calculation, and we believe it should be a valuable signal for the transformer model.
In Graphormer, we use degree centrality as an additional signal for the neural network, which is one of the standard centrality measures in the literature. Specifically, we develop a centrality encoding that assigns two real-valued embedding vectors based on the in-degree and out-degree of each node. Since centrality encoding is applied to each node, we only need to add it as input to the node features.
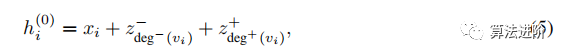
where z-, z+ ∈ Rd are learnable embedding vectors specified by in-degree deg-(vi) and out-degree deg+(vi). For undirected graphs, deg-(vi) and deg+(vi) can be unified as deg(vi). By using centrality encoding in the input, softmax attention can capture the importance signal of nodes in the query and key. Thus, the model can capture both semantic relevance and node importance in the attention mechanism.
3.1.2 Spatial Encoding
The global receptive field of the Transformer allows each token in each layer to attend to information from any position. However, positional dependencies need to be explicitly specified, such as through positional encoding or relative positional encoding.
This article proposes a new spatial encoding method to encode the structural information of the graph in the model. Specifically, for graph G, consider a function φ(vi, vj): V × V → R that measures the spatial relationship between vi and vj in graph G. In this paper, φ(vi, vj) is chosen as the shortest path distance (SPD) between vi and vj if these two nodes are connected. If not, the output of φ is set to -1. A learnable scalar is assigned for each feasible output value, which will serve as a bias term in the self-attention module. Let Aij represent the (i, j) element of the query-key product matrix A, we have
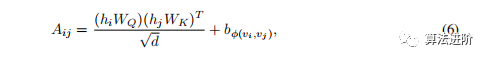
where bφ(vi,vj) is a learnable scalar indexed by φ(vi,vj) shared across all layers.
Our proposed method has the following advantages: Compared to traditional GNNs described in Section 2, the Transformer layer provides global information, allowing each node to attend to all other nodes in the graph, as shown in Equation (6). Additionally, each node can adaptively attend to all other nodes based on the graph structure information. For example, the model may pay more attention to its nearby nodes while paying less attention to those farther away.
3.1.3 Edge Encoding in Attention
In many graph tasks, edges have structural features, such as atom pair features in molecular graphs. Previous work has mainly adopted two edge encoding methods: adding edge features to the relevant node features or using them in aggregation together with node features. However, these methods only propagate edge information to the relevant nodes and may not effectively utilize edge information to represent the entire graph.
This paper proposes a new edge encoding method to better encode edge features into the attention layer. This method considers the edges connecting nodes and computes the average of the dot product of edge features and learnable embeddings along the path. The edge features are integrated into the attention module through a bias term, enhancing the performance of the attention mechanism. Specifically, as shown in Equation (6), we modify the (i, j) element of A in Equation (3) by changing the edge encoding cij to:
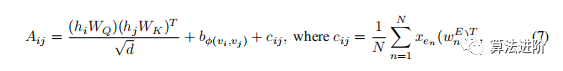
where xen is the feature of the n-th edge en in SPij, wn E ∈ RdE is the n-th weight embedding, and dE is the dimension of the edge features.
3.2 Implementation Details of Graphormer
Graphormer Layer. The Graphormer layer is built on the original implementation of the Transformer encoder, applying layer normalization before the MHA and FFN. For the FFN sublayer, the dimensions of the input, output, and inner layers are set to the same d dimension. The Graphormer layer is formally represented as follows:
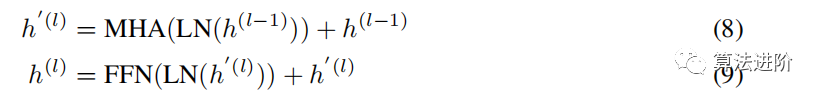
Graph Pooling. In Graphormer, a special node named [VNode] is introduced, connected to each node to represent ordinary nodes in the graph. In the AGGREGATE-COMBINE step, the representation of [VNode] is updated to that of ordinary nodes in the graph, and the representation hG of the entire graph will be the node features of [VNode] in the final layer. This is similar to the [CLS] token in the BERT model, which is used to represent sequence-level features for downstream tasks. Although [VNode] is connected to all other nodes in the graph, the connection is not physical, and the spatial encoding is reset to learnable different scalars to distinguish between physical and virtual connections.
3.3 How Powerful is Graphormer?
This chapter introduces the three structural encodings and architecture of Graphormer and explores whether Graphormer is more powerful than other GNN variants. By demonstrating that Graphormer can represent the AGGREGATE and COMBINE steps in popular GNN models, a positive answer is provided.
The Graphormer layer can represent the AGGREGATE and COMBINE steps in popular GNN models (such as GIN, GCN, GraphSAGE) by selecting appropriate weights and distance functions φ. This result allows the self-attention module to distinguish the neighbor set N(vi) of node vi, calculate the mean statistics of N(vi), and apply multiple heads and FFN to the representations of vi and N(vi). Graphormer can surpass classic message-passing GNNs, with its expressive power not exceeding the 1-Weisfeiler-Lehman (WL) test.
There is a connection between self-attention and virtual nodes. The virtual node trick enhances graphs by adding super nodes, improving GNNs’ performance. Self-attention enables graph-level aggregation and propagation without additional encoding.
The Graphormer layer can represent the average readout function for each node by selecting appropriate weights without additional encoding. By leveraging self-attention, it simulates graph-level readout operations, aggregating information across the entire graph. Experiments show that Graphormer does not suffer from over-smoothing issues, maintaining scalability. The introduction of special nodes for graph readouts is inspired.
4 Experiments
We conducted experiments on the OGB-LSC quantum chemistry regression challenge, which contains over 3.8 million graphs. We also report results on three other popular tasks: ogbg-molhiv, ogbg-molpcba, and ZINC. Detailed descriptions of the datasets and training strategies are provided in Appendix B.
4.1 OGB Large-Scale Challenge
Baseline.Graphormer was benchmarked against GCN, GIN, and their variants, achieving state-of-the-art effective and test mean absolute error. Additionally, Graphormer was compared with the multi-hop variant of GIN and the 12-layer deep graph network DeeperGCN, and performed excellently on other leaderboards. Finally, Graphormer was compared with the Transformer-based graph model GT.
Settings.We report results for two model sizes: Graphormer (L = 12, d = 768) and GraphormerSMALL (L = 6, d = 512). The number of attention heads and the dimension of edge features dE are both 32. Using the AdamW optimizer, hyperparameters are set to 1e-8, with (β1, β2) as (0.99, 0.999). The peak learning rate is 2e-4 (3e-4 for GraphormerSMALL), with a warm-up phase of 60k steps, employing a linear decay learning rate scheduler. A total of 1M training steps were conducted with a batch size of 1024. All models were trained for about 2 days on 8 NVIDIA V100 GPUs.
Results.Table 1 compares the performance on the PCQM4M-LSC dataset. GIN-VN achieved the state-of-the-art validation MAE of 0.1395. The original implementation of GT used 64 hidden dimensions to reduce parameters. For a fair comparison, we also report results with hidden dimensions increased to 768, namely GT-Wide, with a total parameter count of 83.2M. However, both GT and GT-Wide did not outperform GIN-VN and DeeperGCN-VN. In particular, we did not observe performance improvements from the parameter increase in GT.
Table 1 Results of PCQM4M-LSC. * indicates results quoted from the official leaderboard [21].
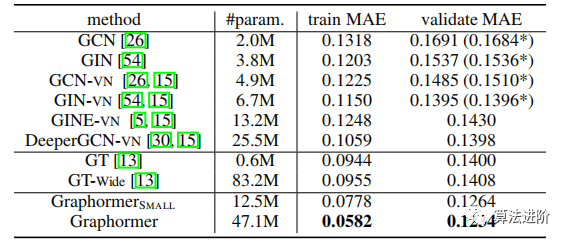
Graphormer outperformed GIN-VN in relative validation MAE, decreasing by 11.5%. By integrating with ExpC, it achieved 0.1200 MAE on the full test set, ranking first in the OGB large-scale challenge graph-level track. Graphormer did not experience over-smoothing issues, with training and validation errors continuously decreasing as the model depth and width increased.
4.2 Graph Representation
This section investigates the performance of Graphormer on graph-level prediction tasks on popular leaderboards (OGB and ZINC). The Graphormer model was pre-trained on OGB-LSC to explore its transferability. For ZINC, which discourages large pre-trained models, Graphormer slim (L=12, d=80, total parameters=489K) was trained from scratch.
Baseline.We report the best performance of GNNs on the official leaderboard without additional domain-specific features. We also report the performance of GIN-VN on the PCQM4M-LSC dataset, which achieved previously state-of-the-art effective and test MAE.
Settings.We report detailed training strategies in Appendix B. Due to the large model size and small dataset size, Graphormer is prone to overfitting. Therefore, we employed FLAG data augmentation techniques to alleviate overfitting issues on the OGB dataset.
Results.Tables 2, 3, and 4 summarize the performance comparison of Graphormer with other GNNs. Graphormer outperformed other GNNs on the MolHIV, MolPCBA, and ZINC datasets, including the Transformer-based GT and SAN. Other pre-trained GNNs did not achieve competitive performance, consistent with previous literature. More comparisons are available in Appendix C.
Table 2 Results of MolPCBA
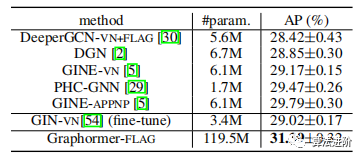
Table 3 Results of MolHIV
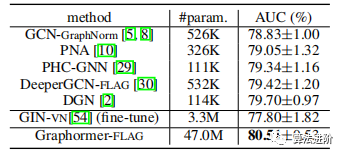
Table 4 Results of ZINC
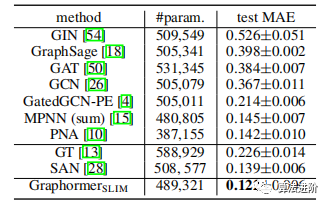
4.3 Ablation Studies
On the PCQM4M-LSC dataset, we conducted ablation studies on Graphormer using a 12-layer Transformer model trained for 100K iterations, with results shown in Table 5.
Table 5 Ablation study results on different designs of the PCQM4M-LSC dataset
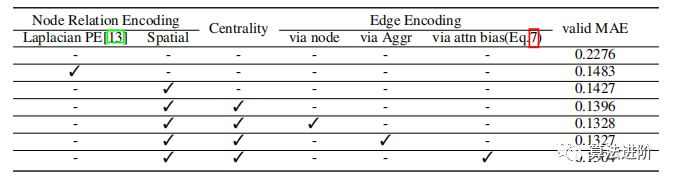
Node Relationship Encoding. We compared positional encoding (PE) and spatial encoding, finding that spatial encoding effectively encodes the information of different node relationships in Transformers. Previous GNNs used WL-PE and Laplacian PE, and we report the performance of Laplacian PE as it performed well in the literature [13]. The Transformer architecture using spatial encoding outperformed the corresponding architecture based on positional encoding, indicating that spatial encoding is effective in capturing spatial information of nodes.
Centrality Encoding. Degree-based centrality encoding in the Transformer architecture significantly enhances performance, indicating its importance for modeling graph data.
Edge Encoding. Our proposed edge encoding (attention bias) was compared with two commonly used edge encoding methods (node and aggregation) to integrate edge features into GNNs. The results show that our proposed method performs significantly better than traditional methods, indicating that edge encoding as an attention bias captures spatial information of the Transformer more effectively.
5 Related Work
This section focuses on GNNs or graph structure encoding based on the Transformer architecture, with less emphasis on work applied to GNNs through attention mechanisms.
5.1 Graph Transformers
Several papers have studied the performance of pure Transformer architectures on graph representation tasks, such as [46], which modified the Transformer layers to use additional GNNs to generate Q, K, and V vectors, long-range residual connections, and two-branch FFNs to produce node and edge representations, fine-tuning on downstream tasks to achieve excellent results. [41] modified the attention module by adding adjacency matrices and inter-atomic distance matrices to the attention probabilities. [13] suggested that the attention mechanism in Transformers on graph data should only aggregate information from neighbors and recommended using Laplacian eigenvectors as positional encodings. [28] proposed a novel full Laplacian spectrum to learn the position of each node in the graph, empirically showing better results than GT.
5.2 Structural Encoding in GNNs
Paths and Distances in GNNs.Path and distance information is widely used in GNNs. For example, attention-based aggregation methods combine node, edge, distance, and cycle flag features to compute attention probabilities. Another method utilizes path-based attention to simulate the influence of central nodes on their higher-order neighbors. There are also aggregation schemes based on distance weighting on graphs. Distance encoding has been shown to have stricter expressive power than the 1-WL test.
Positional Encoding (PE) in Graph Transformers.Several works have introduced positional encoding to help Transformer-based GNNs capture node position information. Graph-BERT uses three types of PE, including absolute WL-PE and two subgraph-based variants of proximity and jump degree. Absolute Laplacian positional encoding was adopted in [13], outperforming the absolute WL-PE used in [61].
Edge Features.This paper also proposed several methods to utilize edge features, including attention-based GNN layers, encoding edge features into GIN, projecting edge features into embedding vectors multiplied by attention coefficients, and sending the results to additional FFN sublayers to produce edge representations.
6 Conclusion
We have explored the direct application of Transformers to graph representation, proposing Graphormer, which performs well on various popular benchmark datasets. However, challenges remain, such as the quadratic complexity of the self-attention module limiting applications on large graphs. Future work needs to develop efficient Graphormers and utilize domain knowledge-based encoding to enhance performance. Additionally, suitable graph sampling strategies for node representation extraction in Graphormer remain for future work.