1. Neuron Models
2. Encoding Methods
3. Learning Algorithms
4. Network Structures
5. Summary and Outlook
In 1997, Wolfgang Maass proposed in his paper “Networks of Spiking Neurons: The Third Generation of Neural Network Models” that networks composed of spiking neurons—spiking neural networks (SNN)—could exhibit more powerful computational characteristics and would become the “third generation of neural network models” [6]. In the early stages of SNN development, its training process leaned more towards the use of synaptic plasticity rules to pursue biological rationality. However, due to the local weight optimization characteristics of rules like Hebbian learning and spike-timing-dependent plasticity, the advantages of SNN in computational characteristics have not been well explored [12,13]. With the resurgence of deep learning, SNN research has increasingly shifted towards performance pursuit, and methods for converting ANN to SNN and proxy gradient-based backpropagation methods have matured. Currently, in AI applications, SNNs with sufficient simulation time can achieve performance comparable to ANNs, providing confidence for the further development of SNNs and the development of neuromorphic hardware.
In this article, I would like to introduce some examples and ideas of biologically inspired SNN designs from four directions: neuron models, encoding methods, learning algorithms, and network structures, and finally summarize and outlook the significance of brain-inspired approaches for SNN research aimed at AI applications.
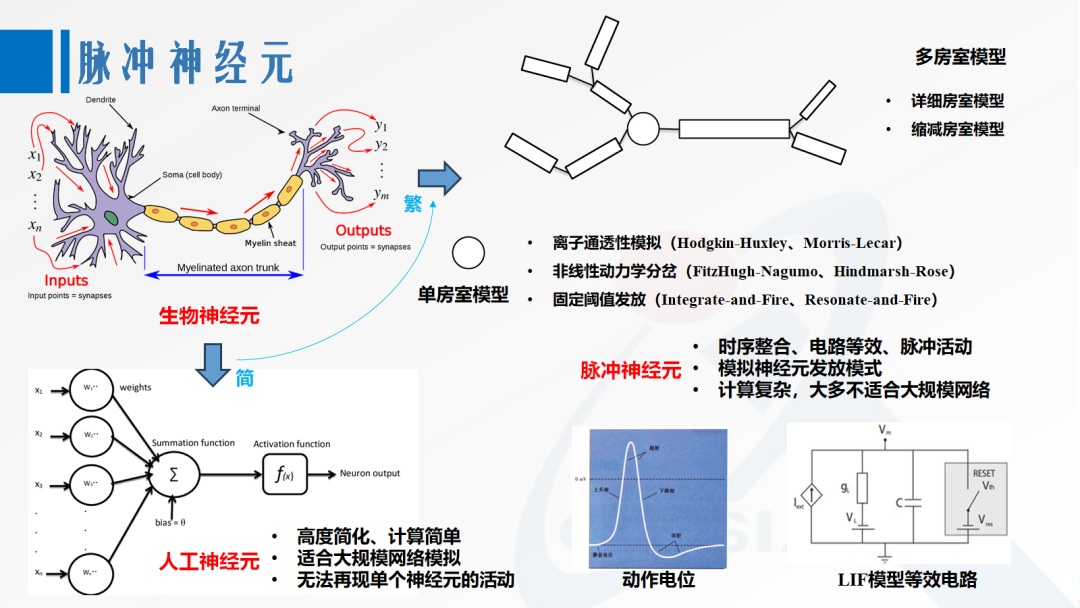
To simulate the activity patterns of biological neurons, computational neuroscience has proposed a series of spiking neuron models. Compared to artificial neurons that use activation functions, spiking neurons generally have characteristics of temporal information integration and suprathreshold spiking activity. Based on the spatial complexity of dendritic and axonal modeling, spiking neurons can be divided into single-compartment models, reduced-compartment models, and detailed-compartment models. In the single-compartment model, there are also different modeling approaches for excitable membranes, such as the Hodgkin-Huxley model and Morris-Lecar model based on different ion permeabilities, the FitzHugh-Nagumo model and Hindmarsh-Rose model based on nonlinear dynamical bifurcations, and the integrate-and-fire model and resonate-and-fire model based on fixed thresholds and reset mechanisms.
Figure 1. Models of Spiking Neurons
Due to computational complexity, most spiking neuron models are not suitable for large-scale simulations similar to artificial neural networks. Wolfgang Maass used a relatively simple integrate-and-fire model when proposing SNN, while the leaky integrate-and-fire (LIF) model [1] is currently the most commonly used spiking neuron in AI-oriented SNN research. Some works on SNN learning algorithms draw an analogy between LIF neurons and recurrent neurons, allowing SNNs to better integrate into the deep learning framework.
[1] Dayan P, Abbott L F. Theoretical neuroscience: computational and mathematical modeling of neural systems [M]. MIT press, 2005.
Although the LIF model possesses the basic properties of spiking neurons, its one-dimensional linear dynamical membrane potential integration process is also considered “too simple to produce the rich firing patterns typical of cortical neurons.” A common method to enhance neuronal dynamical characteristics is to introduce adaptive variables to form a two-dimensional system with membrane potential, which can be interpreted as adaptive threshold changes or internal recovery variables. The Izhikevich neuron [2] further replaces linear dynamics with nonlinear dynamics and generates firing pattern heterogeneity through a set of parameters. Related work inspired by this model indicates that heterogeneous firing patterns can influence the network’s ability to process different types of information, and mixed networks can simultaneously achieve performance advantages on multiple tasks. Other experiments have shown that time constant heterogeneity obtained from training and initialization endows SNNs with robustness, enabling them to learn in a wide range of environments [3].
[2] Izhikevich E M. Simple model of spiking neurons [J]. IEEE transactions on neural networks, 2003, 14(6): 1569-1572.
[3] Perez-Nieves N, Leung V C H, Dragotti P L, et al. Neural heterogeneity promotes robust learning[J]. Nature communications, 2021, 12(1): 5791.
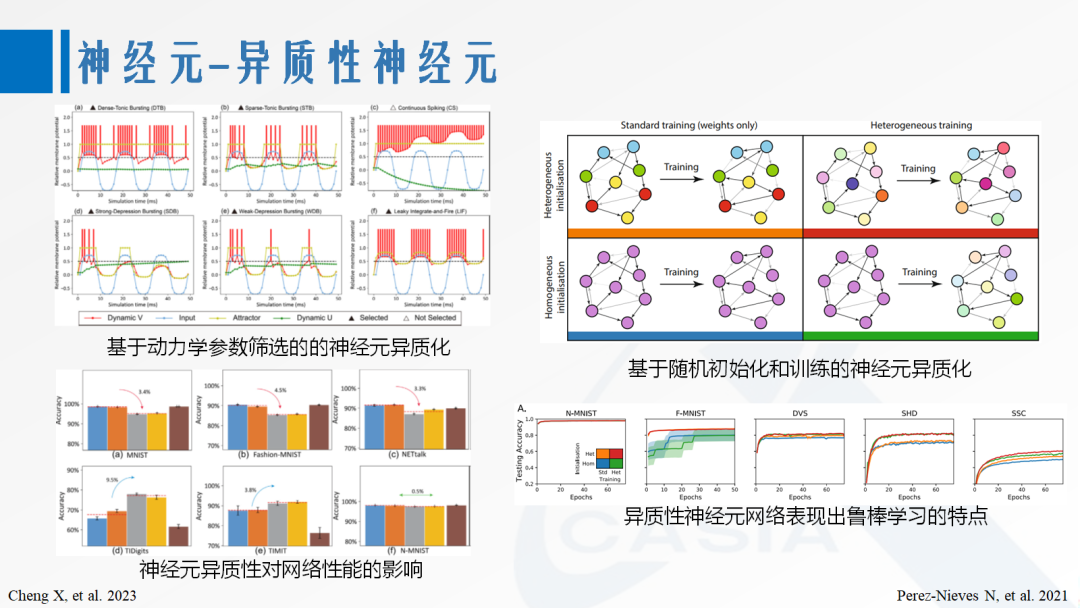Figure 2. Neuronal Heterogeneity
The inherent temporal structure of spiking neurons gives rise to the need for spiking neural networks to serialize non-sequential input information. Based on the encoding methods of biological nervous systems to external stimuli, many encoding methods that effectively store information in spike sequences have been proposed, including rate coding, temporal coding, population coding, sparse coding, and mixed encoding of various coding methods. Among them, frequency coding, which utilizes the firing frequency of spikes within discrete time intervals, is the most commonly used, but it neglects the relationship between the timing of neuronal firing and the information being encoded [4]. Temporal coding can utilize the timing of spikes, thus being more precise than frequency coding, but it is also more complex and prone to higher inference delays [5].
[4] Adrian E D, Zotterman Y. The impulses produced by sensory nerve-endings: Part ii. the response of a single end-organ [J]. The Journal of physiology, 1926, 61(2): 151.
[5] VanRullen R, Guyonneau R, Thorpe S J. Spike times make sense [J]. Trends in neurosciences, 2005, 28(1): 1-4.
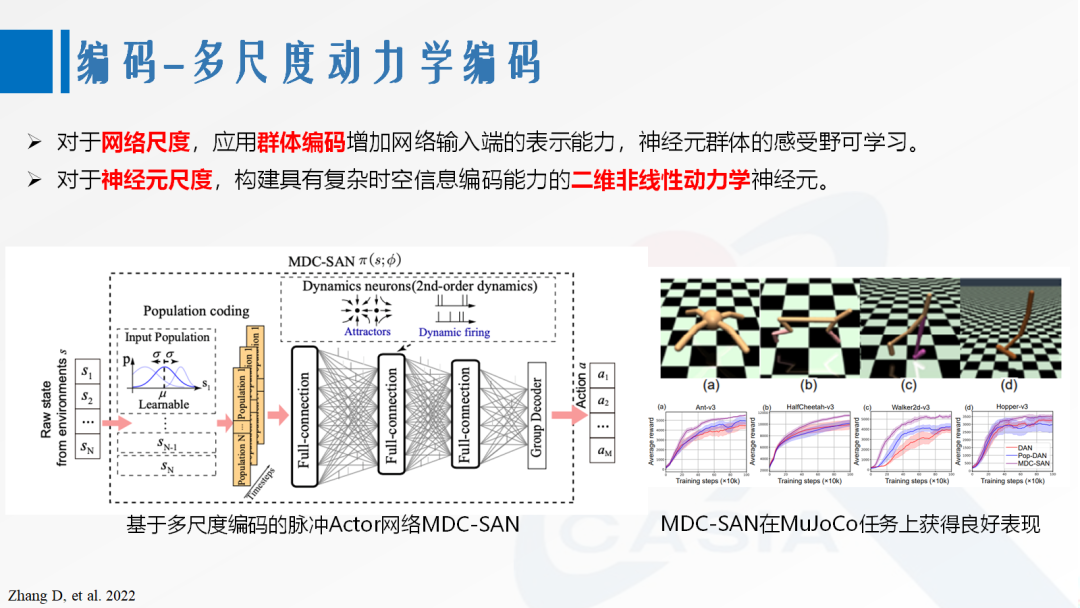
Population coding and sparse coding consider the scenario of representing information through the joint activity of multiple neurons. In population coding, each neuron corresponds to a portion of the features of a class of information and can respond to multiple classes of information simultaneously [6]. This encoding method can reduce instability caused by abnormal activities, expand the information representation space, and quickly respond to changes in information. Meanwhile, the complexity of population coding is relatively low, thus having great application potential. In sparse coding, each neuron in the population responds only to a specific type of information, and each type of information activates only a small number of neurons [7]. This encoding method, often found in memory-related neuronal populations, can reduce interference between pieces of information, thus ensuring the accuracy of memory.
Figure 3. Multi-scale Dynamic Coding
[6] Pouget A, Dayan P, Zemel R. Information processing with population codes [J]. Nature reviews neuroscience, 2000, 1(2): 125-132.
[7] Olshausen B A, Field D J. Sparse coding of sensory inputs [J]. Current opinion in neurobiology, 2004, 14(4): 481-487.
[8] Zhang D, Zhang T, Jia S, et al. Multi-sacle dynamic coding improved spiking actor network for reinforcement learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2022, 36(1): 59-67.
Based on various encoding methods, it has been verified in neuroscience experiments that neurons transmit different types of information using different coding methods or adopt different coding methods at different stages of encoding [9]. This phenomenon reflects the flexibility of biological systems in processing information, and its application in spiking neural networks is likely key to balancing network performance, latency, and energy consumption.
[9] Panzeri S, Brunel N, Logothetis N K, et al. Sensory neural codes using multiplexed temporal scales [J]. Trends in neurosciences, 2010, 33(3): 111-120.
In the early development of spiking neural networks, research on learning algorithms focused more on pursuing biological rationality. Many synaptic plasticity rules proposed by neuroscience have been used to guide the design of learning algorithms, including Hebbian theory [10], long-term potentiation, long-term depression, and spike-timing-dependent plasticity [11]. These rules integrate local activity information, such as the relative timing of pre- and post-synaptic spikes or firing frequencies. Although plasticity rule algorithms have advantages in biological rationality and computational complexity, their performance has always lagged behind advanced learning algorithms of artificial neural networks, such as backpropagation, due to the difficulty in utilizing global guiding information.
[10] Do H. The organization of behavior [J]. New York, 1949.
[11] Markram H, Lübke J, Frotscher M, et al. Regulation of synaptic efficacy by coincidence of postsynaptic aps and epsps [J]. Science, 1997, 275(5297): 213-215.
With the rise of deep learning in recent years, the demand for performance in spiking neural networks has become increasingly strong. In this process, the technology for converting high-performance artificial neural networks to spiking neural networks has matured [12], and the key bottleneck of training spiking neural networks using backpropagation due to the non-differentiability of the firing process has been addressed through proxy gradients [13]. These two methods have become mainstream learning algorithms for spiking neural networks.
[12] Cao Y, Chen Y, Khosla D. Spiking deep convolutional neural networks for energy-efficient object recognition [J]. International journal of computer vision, 2015, 113: 54-66.
[13] Wu Y, Deng L, Li G, et al. Spatio-temporal backpropagation for training high-performance spiking neural networks [J]. Frontiers in neuroscience, 2018, 12: 323875.
Some works also attempt to borrow biological rules to realize supervised learning in SNNs. Among them, neuromodulation is a commonly focused global information propagation method. Three-factor learning introduces the influence of neuromodulation in addition to the activities of pre- and post-synaptic neurons [14]. Here, local plasticity is usually accumulated in the form of eligibility traces and acts on synaptic weights after “reward” delays. Another modeling approach for neuromodulation is meta-plasticity, which models changes in the amplitude and polarity of plasticity as a function of neuromodulator levels to achieve efficient global confidence distribution [15].
[14] Frémaux N, Gerstner W. Neuromodulated spike-timing-dependent plasticity, and theory of three-factor learning rules [J]. Frontiers in neural circuits, 2016, 9: 85.
[15] Zhang T, Cheng X, Jia S, et al. A brain-inspired algorithm that mitigates catastrophic forgetting of artificial and spiking neural networks with low computational cost[J]. Science Advances, 2023, 9(34): eadi2947.
Some learning algorithms derived from the biological perspective of explaining backpropagation (BP) have also been applied to optimize SNNs and ANNs. BP finds the optimal gradient descent direction by calculating the relationship between weight changes and errors, involving independent feedback pathways, precise error calculations, and coherent bidirectional matrices, which may not necessarily have a material basis in biology. By reducing the precision of the computational process, correspondences can be established between BP and some biological mechanisms: feedback alignment and similar learning algorithms decouple the coherence between bidirectional matrices [16]; the NGRAD framework decomposes learning into a combination of neuronal activity errors and local gradients [17]; self-organizing backpropagation algorithms model the mesoscopic processes of plasticity reverse propagation [18]; and BP-STDP demonstrates the equivalence of STDP and BP under certain conditions [19]. These algorithms may not achieve significant superiority over BP in terms of accuracy, but they can effectively reduce training costs while ensuring accuracy remains close, and this trade-off is of considerable significance for biological survival in the real world.
Figure 4. Development of Approximate Backpropagation (BP) Algorithms
[16] Lillicrap T P, Cownden D, Tweed D B, et al. Random synaptic feedback weights support error backpropagation for deep learning [J]. Nature communications, 2016, 7(1): 13276.
[17] Lillicrap T P, Santoro A, Marris L, et al. Backpropagation and the brain [J]. Nature reviews neuroscience, 2020, 21(6): 335-346.
[18] Zhang T, Cheng X, Jia S, et al. Self-backpropagation of synaptic modifications elevates the efficiency of spiking and artificial neural networks[J]. Science advances, 2021, 7(43): eabh0146.
[19] Tavanaei A, Maida A. BP-STDP: Approximating backpropagation using spike timing dependent plasticity[J]. Neurocomputing, 2019, 330: 39-47.
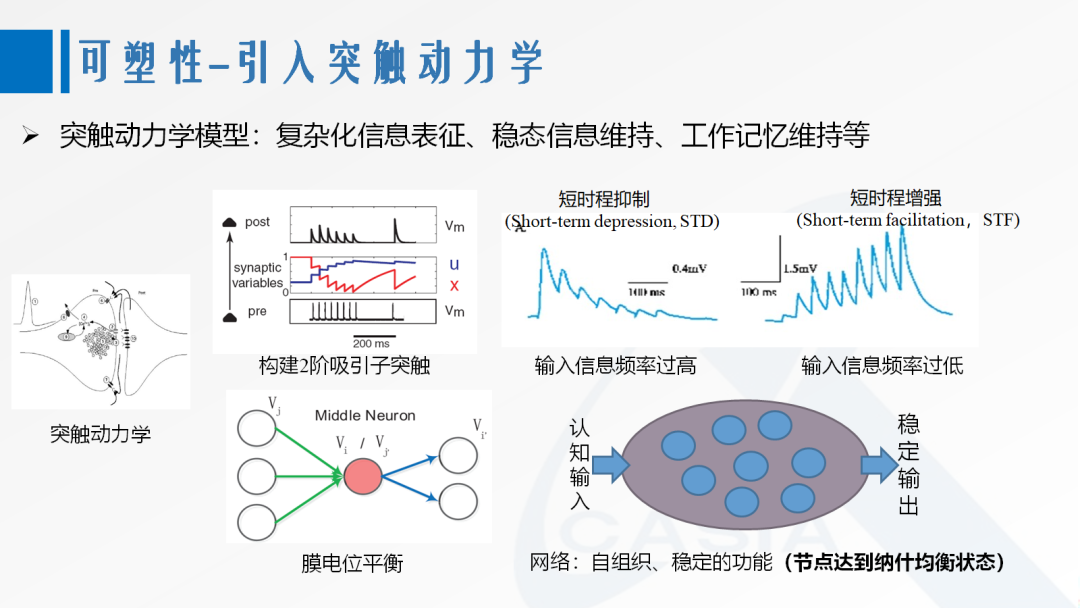
Additionally, some short-term synaptic plasticity mechanisms have been applied in SNNs. Unlike learning algorithms that can form “knowledge” that can be solidified into weights, short-term plasticity [20] corresponds to dynamic scales and often undertakes micro-functions such as complex information representation, steady-state information maintenance, and working memory maintenance.
Figure 5. Synaptic Dynamics Model
[20] Stevens C F, Wang Y. Facilitation and depression at single central synapses [J]. Neuron, 1995, 14(4): 795-802.
Although the connections formed by neurons after long-term evolution have important reference value for artificial networks, currently, spiking neural networks still rely more on the reuse of classical structures in artificial neural networks, including convolutional structures, recurrent structures, residual structures, etc. Biological structural inspirations focus more on non-global scales. The lateral interactions among neurons in the same layer, validated across various perceptual systems, are often discussed as a fundamental structural mechanism triggered by explanations of the Mach band phenomenon. In SNN research, this mechanism is often used to form winner-take-all networks or enhance features while suppressing noise [21]. The tap-withdrawal reflex in the nematode nervous system is controlled by specific loops. Sparse networks constrained by loops can achieve efficient robotic control [22].
[21] Cheng X, Hao Y, Xu J, et al. LISNN: Improving spiking neural networks with lateral interactions for robust object recognition[C]//IJCAI. 2020: 1519-1525.
[22] Hasani R, Lechner M, Amini A, et al. A natural lottery ticket winner: Reinforcement learning with ordinary neural circuits[C]//International Conference on Machine Learning. PMLR, 2020: 4082-4093.
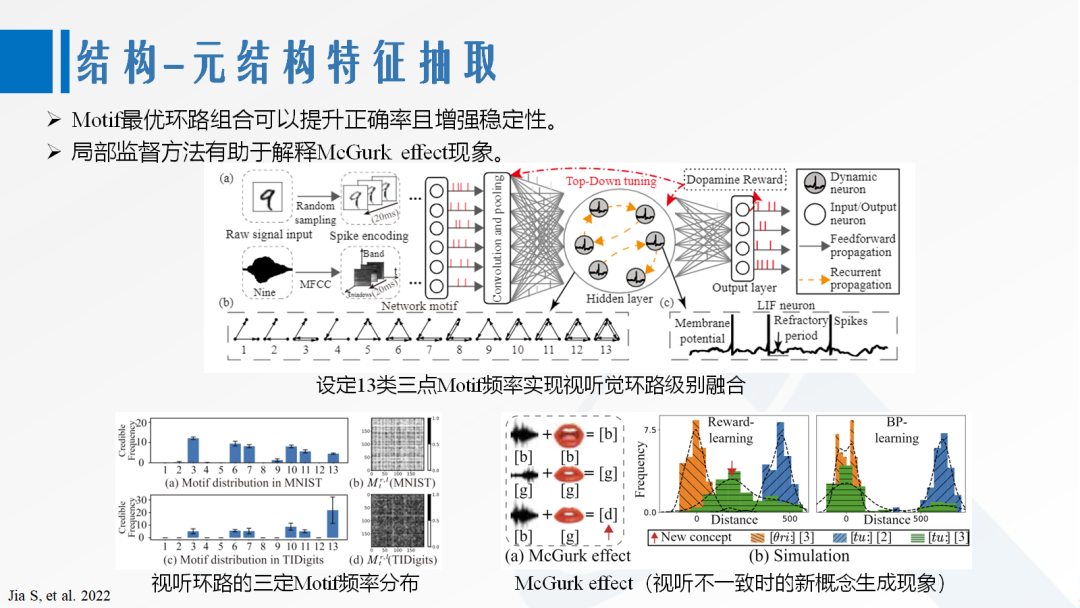
The lottery hypothesis suggests that a large-scale network can find a small-scale sparse network that is functionally equivalent to it, indicating that functional structure extraction in large-scale networks is theoretically possible. Based on this, key structural features and important topological loops can be adjusted to form basic structural operators. Taking the motif distribution as an example, a motif refers to a loop unit containing several neurons, and the proportion of different types of motifs is the motif distribution. Different distributions can form feedforward, feedback, and recurrent connections. Many biological systems have been found to conform to specific motif distributions. Related work based on three-point motif features can achieve loop-level information fusion, enhancing accuracy while reproducing cognitive effects [23].
[23] Zhang D, Zhang T, Jia S, et al. Multi-sacle dynamic coding improved spiking actor network for reinforcement learning[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2022, 36(1): 59-67.
Figure 6. Motif Structural Feature Extraction
With the launch and development of brain projects in various countries, related work on whole-brain mapping is expected to inspire the design of newer network structures with greater integrity. Supported by more biological data, functional structure extraction methods are more likely to find key connection patterns. On the other hand, since the brain is a “general intelligent agent” composed of various functionally distinct brain regions, a possible approach in utilizing prior knowledge from mapping to inspire network structures is to first subtract, forming specific functional reproductions at the level of brain regions, and then add to achieve a general intelligence that approximates the brain.
Figure 7. Whole-Brain Map
As one of the forefront intersections of neuroscience and artificial intelligence, the research on SNN starts from the biological rationality of neuron nodes and has the potential to further integrate brain-inspired approaches, breaking through the current bottlenecks of artificial networks in energy consumption, robustness, stability, and continual learning. However, in the current context where neuroscience development is not yet complete, and there exists a black box between higher brain functions and underlying mechanisms, constructing SNNs purely from biological mechanisms is unlikely to achieve the same level of complex explicit functions as the brain or make significant performance breakthroughs based on deep networks. Instead, a model aimed at functional reproduction and mathematical methods may be more suitable for current brain-like research. However, it is worth noting that brain-like neural network research can also serve as a means to inspire the design of neuroscience experiments, explain relevant experimental results, and predict relationships between functions and mechanisms. The collaborative development of artificial intelligence and neuroscience may be an important way for both to demystify and further develop.
Dr. Cheng Xiang is currently studying at the Institute of Automation, Chinese Academy of Sciences, majoring in pattern recognition and intelligent systems. His research focuses on spiking neural networks, biologically plausible learning algorithms, and brain-computer interface algorithms, with research results published as the first author in top artificial intelligence journals and conferences such as Science Advances, IJCAI, Neurocomputing, and IEEE TNNLS.
Computational Neuroscience Reading Club
The human brain is a complex system composed of billions of interconnected neurons, considered to be “the most complex object in the known universe.” Aiming to promote communication and collaboration among academic workers interested in brain science, brain-like intelligence and computation, and artificial intelligence from various fields such as neuroscience, systems science, information science, physics, mathematics, and computer science, the Intelligence Club has initiated the third season of the series reading club on neuroscience and cognition—”Computational Neuroscience” reading club, covering four major modules: complex neural dynamics, neuron modeling and computation, cross-scale neural dynamics, and the integration of computational neuroscience and AI, and hopes to explore the inspiration of computational neuroscience for brain-like intelligence and artificial intelligence. The reading club will start on February 22, 2024, and will be held every Thursday from 19:00 to 21:00 for an estimated duration of 10-15 weeks. Interested friends are welcome to register and participate, deeply sorting related literature and stimulating interdisciplinary academic sparks!
For more details, see:Launch of the Computational Neuroscience Reading Club: From Complex Neural Dynamics to Brain-like Artificial Intelligence
