Author: Deng Yang
This article is approximately 6300 words long and is recommended for a 10-minute read.
This article briefly introduces the working principles of GAT based on the order discussed in the paper by Velickovic et al. (2017).
When numbers are intangible, intuition is sparse; when forms are few, it is hard to delve deeply – Hua Luogeng
1 Introduction to Graph Attention Networks
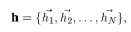(1)
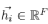represents the input features. Such an input layer will generate new features for the nodes, so the output can be expressed as:
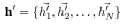(2)
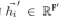To convert the input features into high-dimensional features, at least one linear transformation from a scientific perspective is required. In (Velickovic et al., 2017), the authors used a shared linear transformation for each node and introduced a weight matrix
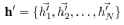to parameterize the linear transformation.
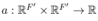Thus, for node i, the importance of node j’s features can be measured by the following equation:
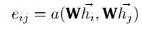(3)
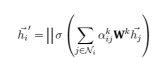(4)
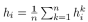or concatenated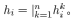
2.3 Step-by-Step Illustration
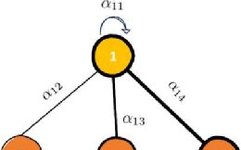
This article refers to the example from (LaBonne, 2022) to better explain how to use the previously mentioned calculation methods in nodes. For node 1’s embedding self-attention calculation method:
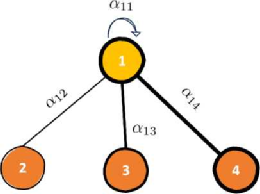
Figure 1: Example Illustration
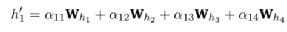(5)
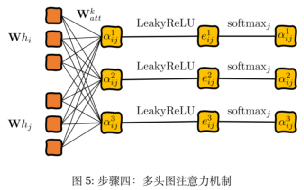
Where αij still represents the importance of the feature relationship between nodes, hi is the attribute vector of each point. Based on the above calculation method, the graph attention mechanism will calculate the embedding value of node 1. As for the graph attention coefficients in the processing equations, they need to be computed through a ‘four-step process’ (LaBonne, 2022): linear transformation, activation function, softmax normalization, and multi-head attention mechanism to learn the attention scores related to node 1.
In the first step, the importance of connections between each point can be calculated by creating hidden vector pairs through concatenating the vectors between two points. To achieve this, a linear transformation and a weight matrix Watt are applied: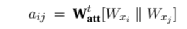 
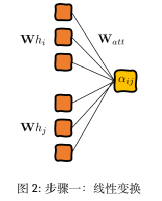(6)
Second step, add an activation function LeakyReLU:
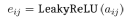
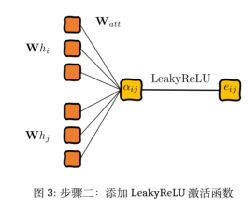(7)
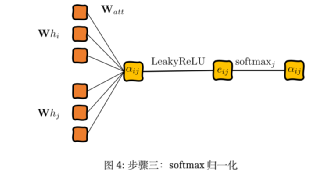
Third step, normalize the output results of the neural network for easier comparison:
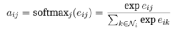
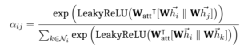Normalized attention scores can be calculated and compared, but at the same time, a new problem arises: self-attention is very unstable. Velickovic et al. (2017) proposed using a multi-head attention mechanism based on the transformer structure.
(8)(9)
Fourth step, according to the previously mentioned multi-head attention mechanism, this is used to process and calculate attention scores:
3 Applications of GAT in Combinatorial Optimization Problems
3.1 Combinatorial Optimization Problems
Combinatorial optimization problems are core issues in operations research and are a necessary path for scholars to begin learning operations research. Combinatorial optimization problems are a core domain in computer science and operations research, involving many practical applications such as logistics, scheduling, and network design. Combinatorial optimization problems play a crucial role in many practical applications. For example, in the logistics field, combinatorial optimization problems can help people find the optimal cargo delivery routes amidst complex transportation conditions, thereby saving transportation costs and improving freight efficiency. In scheduling problems, combinatorial optimization can help effectively allocate resources to meet various constraints while maximizing or minimizing a desired objective value (commonly referred to as the objective function).
However, traditional combinatorial optimization algorithms often require designing from scratch for each new problem and necessitate careful consideration of the problem structure by experts. Solving combinatorial optimization problems typically requires substantial computational resources, especially for real-world problems, where the problem size is often enormous, and traditional optimization algorithms may not find solutions within a reasonable time frame, or even within a reachable time frame. Therefore, how to effectively solve combinatorial optimization problems has been a focal point for researchers. In recent years, using Markov chains to construct dynamic programming has enabled the solution of combinatorial optimization problems expressed as single-player games defined by states, actions, and rewards, including minimum spanning trees, shortest paths, the traveling salesman problem (TSP), and vehicle routing problems (VRP), without expert knowledge. This method uses reinforcement learning to train graph attention neural networks (GNNs), training on unlabelled graph training sets. The trained network can output approximate solutions for new graph instances in linear runtime. In TSP problems, GAT can effectively manage the distance relationships between cities to find the shortest travel path. In VRP problems, GAT can effectively handle the relationships between vehicles, customers, and warehouses to find the optimal delivery routes. These research results indicate that GAT has tremendous potential in solving combinatorial optimization problems.
3.2 Case Study of GAT in Path Planning Papers
(Kool et al., 2018) proposed an attention mechanism-based model similar to GAT to solve various path planning problems, including TSP, VRP, OP, and others. This article primarily constructs path planning problems (such as TSP) as graph-based problems, with each customer point’s location and other information serving as node features. Through an attention mechanism-based encoder-decoder, the path results indicate a random policy π(π|s), using this policy to find the most effective path method π within given test data points, which is parameterized by θ and decomposed into:
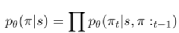(10)
The decoding process is sequential. At each time step, the decoder outputs node πt based on the encoder’s embedding and the output generated at that time. During the decoding process, a special context node is added to represent the decoding context. The decoder computes an attention (sub) layer on top of the encoder, but only sends messages to the context node to improve efficiency. The final probability is calculated using a single-head attention mechanism. At time t, the decoder’s context comes from the encoder and the output prior to time t. For TSP, this includes the graph’s embedding, the previous (last) node πt-1, and the first node π1. Meanwhile, to compute the output probability, a final decoder layer with a single attention head is added. The article optimizes the loss L using gradient descent, employing the REINFORCE gradient estimator and a baseline. The article uses a rollout baseline, with periodic updates to the baseline policy, serving as a better model-defined policy for determining the deterministic greedy rollout solutions.
The article also discusses in detail the handling strategies for different problems. For example, for the reward-collecting traveling salesman problem (PCTSP), the authors use separate parameters in the encoder to handle warehouse nodes and provide node rewards and penalties as input features. In the context of the decoder, the authors use the current/last position and remaining rewards for collection. In PCTSP, if the remaining rewards are greater than 0 and all nodes have not been visited, the warehouse node cannot be accessed. Only when the node has been visited can it be masked (i.e., not accessible).
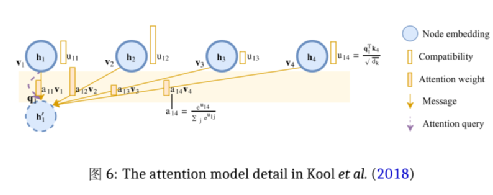
Due to space limitations, this article focuses on how Kool et al. (2018) constructed an algorithm to pass weighted information between nodes in TSP based on the graph attention mechanism. In the constructed graph, the information received by the nodes is weighted and comes from themselves and their neighboring points. The information values of these nodes depend on the compatibility of their queries with their neighbors’ keys, as shown in Figure 6. The authors defined dk, dv and calculated the corresponding ki∈ ℝdk, vi∈ ℝdv, qi∈ ℝdk for all points. Through the following method, all corresponding qi, ki, vi are projected into hi for calculation:
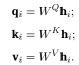
Where WQ, WK are two parameter matrices with dimensions dk × dh, and WV is of size (dv × dh). (Readers interested in a deeper understanding of the settings and calculation methods of q, k, v in Transformer, please refer to WMathor (2020))
The compatibility between two points is realized by calculating the value uij between node i’s qi and node j’s kj (Velickovic et al., 2017):
(12)
Finally, node i will receive a vector h’i that contains a convex combination of vector vj:
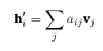(13)
4 Conclusion
4.1 Future Development and Application Prospects of GAT
Graph Attention Networks (GAT) have been widely proven in their ability to solve combinatorial optimization problems, particularly the traveling salesman problem (TSP) and vehicle routing problem (VRP). However, it should also be noted that while GAT has shown superiority in these problems, it is not a panacea. For some specific problems, it may be necessary to design specific models or algorithms to solve them. Therefore, when researching a problem, it is crucial to select appropriate tools to address different combinatorial optimization issues based on the specific circumstances of the problem and the characteristics of GAT in solving problems.
GAT also plays various roles in other fields. For example, Zhang et al. (2022) proposed a new GAT architecture that can capture potential associations between graph knowledge at different scales. This new GAT architecture outperforms traditional GAT models in terms of prediction accuracy and training speed.
Additionally, Shao et al. (2022) proposed a new dynamic multi-graph attention model that can handle long-term spatiotemporal prediction problems. This model constructs new graph models to represent the contextual information of each node and utilizes long-term spatiotemporal data dependency structures. Experiments on two large-scale datasets indicate that it can significantly enhance the performance of existing graph neural network models in long-term spatiotemporal prediction tasks.
In stock market prediction, GAT also has extensive applications. Zhao et al. (2022) proposed a stock movement prediction method based on a dual attention network. First, a market knowledge graph containing two types of entities (including listed companies and related executives) and mixed relationships (including explicit and implicit relationships) is constructed. Then, a dual attention network is proposed, which can learn momentum overflow signals in the market knowledge graph for stock prediction. Experimental results show that this method outperforms nine state-of-the-art baseline methods in stock prediction.
Overall, the graphical perspective provides a new way to understand and solve problems. Thinking about and transforming existing problems into graphical forms not only reveals new aspects and characteristics of the problems but may also spark new innovations. Similarly, thinking about new problems using graphical methods may lead to unexpected gains. The advantage of this approach is that it helps scholars better understand the structure and complexity of problems, thereby finding more effective solutions. It is hoped that readers can gain a better understanding of the principles of graph neural networks from this introduction to GAT and apply it more in their studies and research, providing strong support for problem-solving through the use of GAT.
Author Biography
Author Deng Yang is a joint PhD student from the School of Management at Xi’an Jiaotong University and the School of Systems Engineering at City University of Hong Kong, focusing on the application of reinforcement learning in urban logistics. He graduated with a Master’s degree in Transportation Engineering from the University of Southern California, with honors. He has previously worked at the engineering consulting firm HATCH in Los Angeles, California, and is a registered EIT in California. He has received titles such as ‘Thirty Under Thirty Outstanding Young Entrepreneurs’ from AACYF in 2017 and ‘Top Ten Outstanding Young Chinese Americans’ in 2019. Currently, he serves as the Vice President of the Baotou Overseas Chinese Association and is a member of the Overseas Chinese Federation and the European and American Alumni Association.
Introduction to Datapi Research Department
The Datapi Research Department was established in early 2017, dividing into multiple groups based on interests, each group follows the overall knowledge sharing and practical project planning of the research department while having its own characteristics:
Algorithm Model Group: Actively participates in competitions like Kaggle and produces original step-by-step instructional articles;
Research and Analysis Group: Investigates the applications of big data through interviews and explores the beauty of data products;
System Platform Group: Tracks the cutting edge of big data & artificial intelligence system platform technologies and engages with experts;
Natural Language Processing Group: Focuses on practice, actively participates in competitions and organizes various text analysis projects;
Manufacturing Big Data Group: Adheres to the dream of becoming an industrial powerhouse, integrating production, learning, research, and government to tap into data value;
Data Visualization Group: Merges information with art, explores the beauty of data, and learns to tell stories through visualization;
Web Crawling Group: Crawls web information and collaborates with other groups to develop creative projects.
Click on the end of the article “Read the original text” to sign up as a volunteer for the Datapi Research Department, there is always a group suitable for you~
Click “Read the original text” to join the organization~