The Fastest Way to Train Neural Networks: AdamW Optimization Algorithm + Super Convergence

Excerpt from fast.ai

Authors: Sylvain Gugger, Jeremy Howard

Translated by: Machine Heart

Contributors: Siyuan, Wang Shuting, Zhang Qian

Optimization methods have always been a crucial part of machine learning and are the core algorithms of the learning process. Since its introduction in 2014, Adam has garnered widespread attention, with over 10,047 citations for the original paper. However, many researchers have found that the convergence of the Adam optimization algorithm is not guaranteed. The best paper at ICLR 2017 also focused on its convergence. In this article, the authors discovered that most implementations of Adam in deep learning libraries have issues, and they implemented a new AdamW algorithm in the fastai library. Based on some experiments, the authors state that this algorithm is currently the fastest way to train neural networks.

The Roller Coaster of Adam

The journey of the Adam optimizer can be described as a roller coaster. This optimizer was introduced in 2014 and is essentially a simple idea based on intuition: since we clearly know that certain parameters need to move faster and further, why should every parameter follow the same learning rate? Because the square of the recent gradients tells us how much signal each weight can get, we can divide by this, ensuring that even the slowest weights have a chance to shine. Adam embraced this idea and incorporated standard methods, thus creating the Adam optimizer (with slight adjustments to avoid biases in early batches)!

When it was first published, the deep learning community was excited by some graphs from the original paper (shown below):

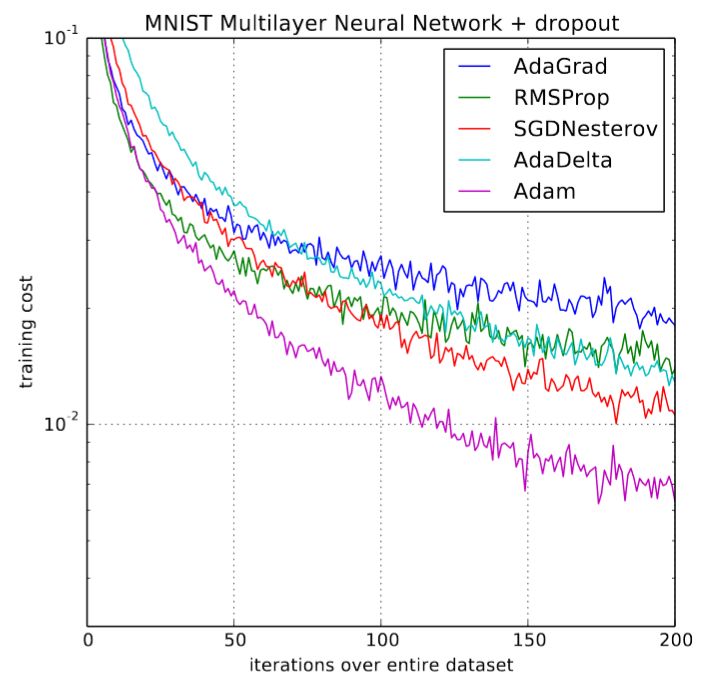
Comparison of Adam and Other Optimizers

Training speed increased by 200%! “Overall, we found Adam to be very robust and widely applicable to various non-convex optimization problems in machine learning,” the paper concluded. That was three years ago, during the golden age of deep learning. However, things did not develop in the direction we expected. Research articles using Adam to train models have become rare, and new studies have begun to noticeably suppress its application, showing in several experiments that SGD + momentum may outperform the complex Adam. By the time the fast.ai course started in 2018, poor Adam had been removed from the early curriculum.

However, by the end of 2017, Adam seemed to regain its vitality. Ilya Loshchilov and Frank Hutter pointed out in their paper “Fixing Weight Decay Regularization in Adam” that every library’s implementation of weight decay on Adam seemed to be incorrect and proposed a simple method (which they called AdamW) to fix it. Although the results varied slightly, they did present some encouraging graphs similar to the ones below:

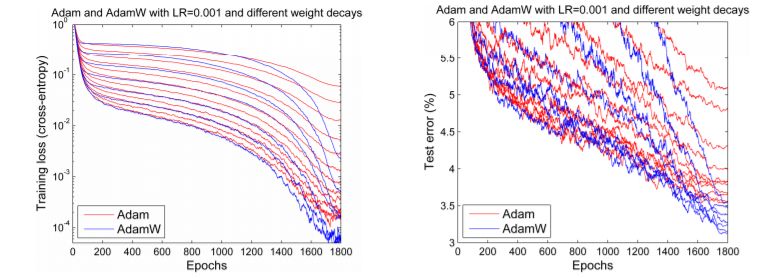
Comparison of Adam and AdamW

We hoped that people would revive their enthusiasm for Adam, as some early results of this optimizer seemed reproducible. But the opposite happened. In fact, the only deep learning framework that applied it was fastai, coded by Sylvain. Due to the lack of widely available frameworks, everyday practitioners had to stick to the old and less effective Adam.

But that wasn’t the only problem. There were many obstacles ahead. Two papers pointed out the apparent issues with Adam’s convergence proof, although one proposed a fix called AMSGrad (which won the “Best Paper” award at the prestigious ICLR conference). However, if we learned anything from this dramatic history (at least by optimizer standards), it’s that nothing is as it seems. Indeed, PhD student Jeremy Bernstein pointed out that the so-called convergence issue is merely a sign of poorly chosen hyperparameters, and perhaps AMSGrad does not solve the problem. Another PhD student, Filip Korzeniowski, presented some early results that seemed to support this frustrating view of AMSGrad.

Starting the Roller Coaster

So what should we, who just want to quickly train accurate models, do? We chose to address this controversy using the method that has resolved scientific debates for centuries—scientific experimentation. All details will be presented later, but first, let’s look at the general results:

• After proper tuning, Adam really works! We achieved the latest training time results on the following tasks:

• Training CIFAR10 until its accuracy exceeds 94% with just 18 epochs or 30 epochs, as in the DAWNBench competition;

• Tuning Resnet50 until its accuracy on the Stanford Cars dataset reaches 90% with just 60 epochs (previously it took 600 epochs to reach the same accuracy);

• Training an AWD LSTM or QRNN from scratch for 90 epochs (or 1.5 hours on one GPU), achieving current optimal perplexity on Wikitext-2 (previous LSTMs required 750 epochs, QRNNs required 500 epochs).

• This means we have observed super convergence using Adam! Super convergence is a phenomenon that occurs when training neural networks with high learning rates, indicating that half the training process is saved. Before AdamW, training CIFAR10 to 94% accuracy required about 100 epochs.

• Compared to previous work, we found that as long as properly tuned, Adam can achieve accuracy comparable to SGD + Momentum on every CNN image problem we tried, and is almost always a bit faster.

• The suggestion that AMSGrad is a poor “solution” is correct. We consistently found that AMSGrad did not yield higher gains in accuracy (or other relevant metrics) than plain Adam / AdamW.

When you hear people say that Adam’s generalization performance is worse than SGD + Momentum, you will almost always find that the hyperparameters they chose for their models are subpar. Typically, Adam requires more regularization than SGD, so when switching from SGD to Adam, ensure to adjust the regularization hyperparameters accordingly.

Structure of the Article:

1. AdamW

1. Understanding AdamW

2. Implementing AdamW

3. AdamW Experiments and AdamW-ish

2. AMSGrad

1. Understanding AMSGrad

2. Implementing AMSGrad

3. Results of AMSGrad Experiments

3. Complete Results Charts

AdamW

Understanding AdamW: Weight Decay vs. L2 Regularization

L2 regularization is a classic method for reducing overfitting, which adds a penalty term to the loss function composed of the square sum of all model weights, multiplied by a specific hyperparameter to control the penalty strength. All equations in this article are expressed in Python, NumPy, and PyTorch style:

final_loss = loss + wd * all_weights.pow(2).sum() / 2

where wd is the hyperparameter we set to control the penalty strength. This can also be called weight decay because every time we apply the original SGD, it’s equivalent to updating the weights using the following equation:

w = w - lr * w.grad - lr * wd * w

where lr represents the learning rate, w.grad represents the derivative of the loss function with respect to w, and the term wd * w represents the derivative of the penalty term with respect to w. In this equation, we see that every update will subtract a small portion of the weight, which is the source of the “decay”.

All libraries reviewed by fast.ai used the first form. In practice, almost all achieve the algorithm by adding gradient wd*w rather than actually altering the loss function. Because we do not want to add extra computation to correct the loss, especially when simpler methods are available.

Since they are the same expression, why do we need to distinguish between these two concepts? The reason is that they are only equivalent for the original SGD, and when we add momentum or use more complex optimization methods like Adam, L2 regularization (the first equation) and weight decay (the second equation) can differ significantly. In the rest of this article, when we discuss weight decay, we refer to the second equation, while L2 regularization refers to the first classic method.

As shown in SGD with momentum, L2 regularization and weight decay are not equivalent. L2 regularization adds wd*w to the gradient, but now the weights are not directly subtracted from the gradient. First, we need to compute the moving average:

moving_avg = alpha * moving_avg + (1-alpha) * (w.grad + wd*w)

Then the weights can be updated by subtracting the moving average multiplied by the learning rate. Thus, the weight decay update can be represented as:

moving_avg = alpha * moving_avg + (1-alpha) * w.grad 
w = w - lr * moving_avg - lr * wd * w

We can observe that the subtraction of the regularization part from w is different in the two methods. When using the Adam optimizer, the weight decay part may differ even more. Because L2 regularization in Adam requires adding wd*w to the gradient and separately computing the moving averages of the gradient and its square before updating the weights. However, the weight decay method simply updates the weights and subtracts a little from the weights each time.

Clearly, these are two different methods, and after experiments, Ilya Loshchilov and Frank Hutter suggested that we should use the weight decay method in the Adam algorithm instead of L2 regularization as implemented in classic deep learning libraries.

Implementing AdamW

So how can we implement the AdamW algorithm? If you are using the fastai library, you can simply implement it by adding the parameter use_wd_sched=True when using the fit function:

learn.fit(lr, 1, wds=1e-4, use_wd_sched=True)

If you prefer the new training API, you can use the parameter wd_loss=False in each training phase:

phases = [TrainingPhase(1, optim.Adam, lr, wds=1e-4, wd_loss=False)]
learn.fit_opt_sched(phases)

The following briefly outlines how fastai implements AdamW. In the optimizer’s step function, we only need to use the gradient correction parameter, not the value of the parameter itself (except for weight decay, which we will handle externally). We can implement weight decay before the optimizer, but it still needs to be done after calculating the gradient; otherwise, it will affect the value of the gradient. So in the training loop, we must determine when to compute the weight decay.

loss.backward()
# Do the weight decay here!
optimizer.step()

Of course, the optimizer should set wd=0; otherwise, it will also perform some L2 regularization, which we do not want to see. Now in the weight decay position, we can write a loop statement over all parameters and apply the weight decay updates sequentially. Our parameters should be stored in the optimizer’s param_groups dictionary, so this loop should be represented as follows:

loss.backward()
for group in optimizer.param_groups():
    for param in group['params']:
        param.data = param.data.add(-wd * group['lr'], param.data)
optimizer.step()

AdamW Experimental Results: Does It Really Work?

We first tested it on computer vision problems, and the results were excellent. Specifically, Adam and L2 regularization achieved an average accuracy of 93.96% over 30 epochs, with one of the two trials exceeding 94%. We chose 30 epochs because 94% accuracy can be achieved with the 1cycle strategy and SGD. When we used Adam with the weight decay method, we consistently achieved accuracy between 94% and 94.25%. For this, we found that the optimal beta2 value during the 1cycle strategy was 0.99. We considered the beta1 parameter as the momentum in SGD, which means that it decreases the learning rate from 0.95 to 0.85 and then increases back to 0.95 as the learning rate decreases.

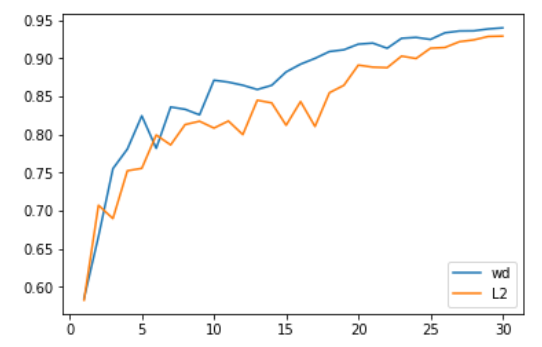
Accuracy of L2 Regularization vs. Weight Decay

More impressively, using test-time augmentation (i.e., averaging predictions on one image from the test set and its four augmented versions), we achieved 94% accuracy in just 18 epochs (average 93.98%)! With simple Adam and L2 regularization, we would exceed 94% once every 20 attempts.

One point to consider in these comparisons is that changing the regularization method alters the optimal values for weight decay or learning rate. In our tests, the optimal learning rate for L2 regularization was 1e-6 (maximum learning rate was 1e-3), while the optimal value for weight decay was 0.3 (learning rate was 3e-3). In all our tests, the order of magnitude differences were very consistent, mainly because L2 regularization was effectively divided by the average norm of the gradients (which was quite low), and Adam’s learning rate was relatively small (so the weight decay updates needed a stronger coefficient).

So, is weight decay always better than L2 regularization in Adam? We haven’t found any noticeably worse cases yet, but whether in transfer learning problems (like fine-tuning Resnet50 on the Stanford Cars dataset) or RNNs, it has not yielded better results.

AMSGrad

Understanding AMSGrad

AMSGrad was introduced by Sashank J. Reddi, Satyen Kale, and Sanjiv Kumar in a recent paper. By analyzing the convergence proof of the Adam optimizer, they discovered an error in the update rule that could lead the algorithm to converge to suboptimal points. They designed theoretical experiments to demonstrate the circumstances under which Adam fails and proposed a simple solution. Machine Heart has also analyzed this award-winning paper from the perspective of adaptive learning rate algorithms: Beyond Adam.

To better understand the error and solution, let’s look at Adam’s update rule:

avg_grads = beta1 * avg_grads + (1-beta1) * w.grad
avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)
w = w - lr * avg_grads / sqrt(avg_squared)

We just skipped the bias correction (which is useful for the start of training) and focused on the main point. The authors found the error in Adam’s convergence proof to be:

lr / sqrt(avg_squared)

This is a step we take in the direction of the average gradient, gradually decreasing during training. Since the learning rate is often constant or decreasing, the authors proposed a solution by tracking their maximum values with an additional variable, thus forcing avg_square to increase.

Implementing AMSGrad

The related paper won an award at ICLR 2018 and has been widely adopted, already implemented in two major deep learning libraries—PyTorch and Keras. So, we just need to pass the parameter amsgrad=True.

avg_grads = beta1 * avg_grads + (1-beta1) * w.grad
avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)
max_squared = max(avg_squared, max_squared)
w = w - lr * avg_grads / sqrt(max_squared)

AMSGrad Experimental Results: A Lot of Noise Is Useless

The results for AMSGrad were very disappointing. In all experiments, we found it to be of no help. Even though the minimum found by AMSGrad was sometimes slightly lower than that reached by Adam (in terms of loss), its metrics (accuracy, f_1 score…) were always worse (see the table in the introduction).

The convergence proof of the Adam optimizer in deep learning (because it targets convex problems) and the errors they found in it are important for synthetic experiments that are unrelated to real-world problems. Practical tests show that when these avg_square gradients want to decrease, doing so yields the best results.

This indicates that even though focusing on theory helps generate some new ideas, nothing can replace experimentation (and a lot of experimentation!) to ensure these ideas genuinely help practitioners train better models.

Appendix: All Results

Training CIFAR10 from scratch (model is Wide-ResNet-22, the following are the average results of five models):

Fine-tuning Resnet 50 on the Stanford Cars dataset with standard heads introduced by fastai (training the head for 20 epochs before unfreezing and training for 40 epochs with different learning rates):

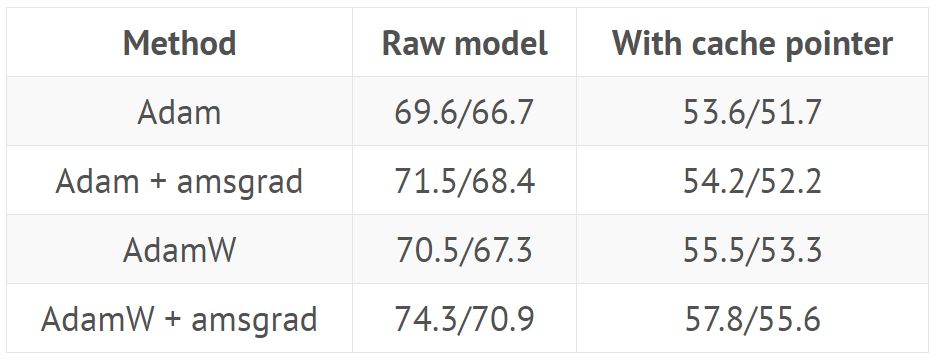
Training AWD LSTM with hyperparameters from GitHub (https://github.com/salesforce/awd-lstm-lm), showing perplexity on validation/test sets with or without cache pointers:

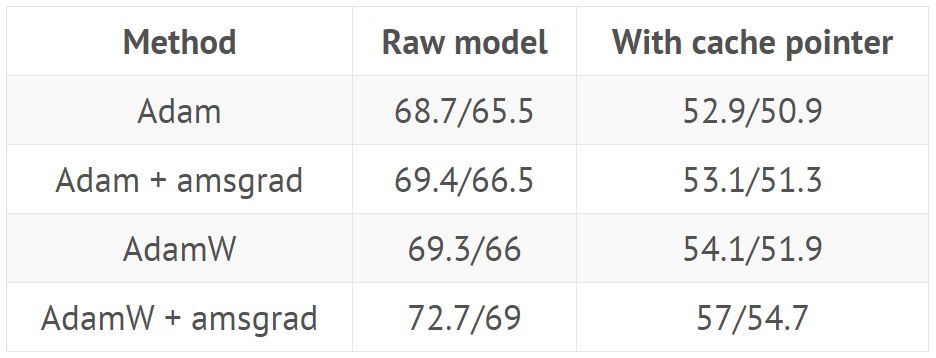
Training QRNN with hyperparameters from GitHub repo, showing perplexity on validation/test sets with or without cache pointers:

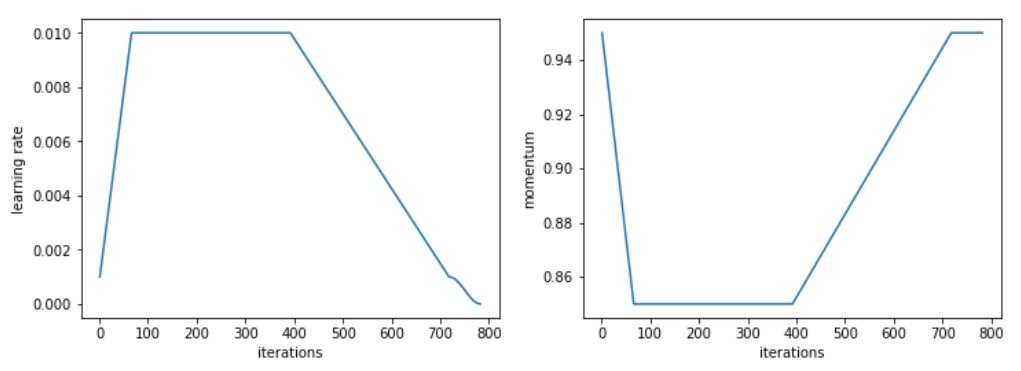
For this specific task, we adopted a modified version of the 1cycle strategy, speeding up the learning rate and then maintaining a high constant learning rate for a long time before decreasing it.

Comparison between Adam and Other Optimizers

All relevant hyperparameter values and the code used to produce these results can be found at: https://github.com/sgugger/Adam-experiments

Original link: http://www.fast.ai/2018/07/02/adam-weight-decay/