Selected from severelytheoretical
Translated by Machine Heart
Contributors: Jiang Siyuan, Liu Xiaokun
The author demonstrates through the example of deep linear networks that the reason for the poor performance of the final network is not vanishing gradients, but rather the degeneracy of the weight matrices, which reduces the effective degrees of freedom of the model, and points out that this conclusion can be generalized to nonlinear networks.
In this article, I will highlight a common misunderstanding regarding the difficulties in training deep neural networks. People often believe that these difficulties are primarily (if not entirely) due to the vanishing gradient problem (and/or the exploding gradient problem). “Vanishing gradient” refers to the phenomenon where the gradient norm of parameters decreases exponentially with the increase in network depth. A small gradient means slow changes in parameters, which stalls the learning process until the gradient becomes sufficiently large, which often requires an exponential amount of time. This idea can be traced back at least to the paper by Bengio et al. in 1994: “Learning long-term dependencies with gradient descent is difficult,” and it seems to remain the preferred explanation for the training difficulties of deep neural networks.
Let us first consider a simple scenario: training a deep linear network to learn a linear mapping. Of course, from a computational perspective, deep linear networks are not interesting, but the paper by Saxe et al. in 2013 “Exact solutions to the nonlinear dynamics of learning in deep linear neural networks” shows that the learning dynamics in deep linear networks can still provide insights into the learning dynamics of nonlinear networks. Therefore, we start our discussion from these simple scenarios. The following figure shows the learning curve of a 30-layer network (the error line is the standard deviation obtained from 10 independent runs) and the initial gradient norm (before training).
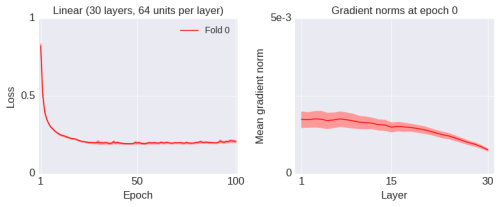
I will briefly explain the meaning of the label “Fold 0” in the figure later. Here, the gradient is regarding the layer activation values (similar to the behavior of gradients with respect to parameters). The weights of the network are initialized using standard initialization methods. Initially, the training loss function decreases rapidly but soon converges to a suboptimal value. At this point, the gradients do not vanish (or explode), at least in the initial phase. The gradients do indeed become smaller during the training process, but this is expected, and in no way indicates that the gradients have become “too small”:
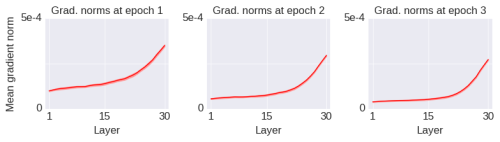
To illustrate that the phenomenon of convergence to a local optimum is unrelated to the size of the gradient norm itself, I will introduce an operation that increases the value of the gradient norm but makes the network’s performance worse. As shown in the figure below (blue line):
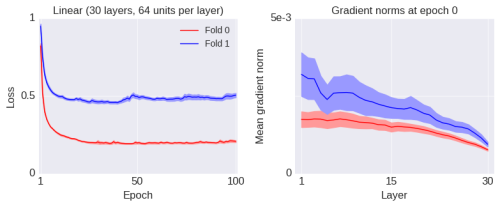
I simply changed the initialization method. All initial weights of the initial network are matrices (initialized using standard methods). In the blue line of the figure above, I merely copied the upper half of each initial weight matrix to the lower half (i.e., the initial weight matrix was folded once, thus called the “Fold 1” network). This operation reduces the rank of the initial weight matrices, making them more degenerate. Note that this operation is only applied to the initial weight matrices and does not impose any other constraints on the learning process, which remains unchanged. After several epochs of training, the changes in gradient norms are shown in the figure below:

Thus, I introduced an operation that increases the global gradient norm, but the performance degrades significantly. Conversely, I will now introduce another operation that reduces the gradient norm yet greatly enhances the network’s performance. As shown in the figure below (green line):
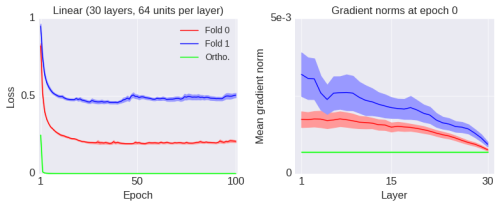
As indicated by the label “Ortho” in the figure, this operation initializes the weight matrices to be orthogonal. Orthogonal matrices are the least degenerate among matrices with fixed (Frobenius) norms, where degeneracy can be measured in various ways. Below are the gradient norms after several epochs of training:
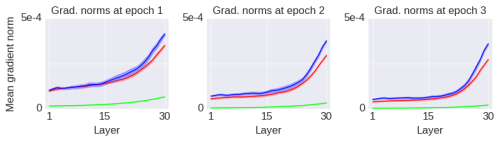
If the size of the gradient norm itself is unrelated to the training difficulties of deep networks, what is the reason? The answer is that the degeneracy of the model fundamentally determines the training performance. Why does degeneracy impair training performance? Intuitively, the learning curve essentially slows down in the degenerate directions of the parameter space, thus reducing the effective dimensionality of the model. Previously, you might have thought of fitting the model with parameters, but in reality, due to degeneracy, the degrees of freedom that can effectively fit the model have decreased. The issues with the “Fold 0” and “Fold 1” networks are that while the gradient norm values are decent, the usable degrees of freedom of the network contribute very unevenly to these norms: although some degrees of freedom (non-degenerate) contribute to the majority of the gradient, most (degenerate) degrees of freedom contribute nothing to this (for conceptual understanding, it is not a very accurate explanation. It can be understood that in each layer, only a small number of hidden units change their activation values for different inputs, while most hidden units respond the same way to different inputs).
As demonstrated by Saxe et al., as the number of multiplied matrices (i.e., network depth) increases, the product of the matrices becomes more degenerate (linearly correlated). Below are examples from their paper of 1-layer, 10-layer, and 100-layer networks:
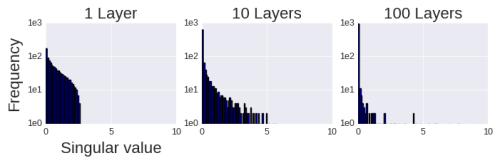
As the network depth increases, the singular values of the product matrices become increasingly concentrated, while a small number of infrequently occurring singular values become arbitrarily large. This result is not only related to linear networks. A similar phenomenon occurs in nonlinear networks: as depth increases, the dimensionality of the hidden units in a given layer becomes lower and lower, that is, more degenerate. In fact, in nonlinear networks with hard saturation boundaries (e.g., ReLU networks), the degeneration process accelerates as depth increases.
The paper by Duvenaud et al. in 2014, “Avoiding pathologies in very deep networks,” visualizes this degeneration process:

As depth increases, the input space (top left) distorts into increasingly thin filaments at every point, and only one direction orthogonal to the filament influences the network’s response. It may be difficult to represent the changes in the input space in two dimensions, but experiments show that points in the input space become locally “hyper-pancakey”, meaning that each point has a single direction orthogonal to the distorted surface. If we change the input along this sensitive direction, the network is actually very sensitive to the changes.
Finally, I can’t help but mention the paper I wrote with Xaq Pitkow. In the paper “SKIP CONNECTIONS ELIMINATE SINGULARITIES,” we demonstrated through a series of experiments that the degeneration problem discussed in this article severely affects the training of deep nonlinear networks, and skip connections (an important method used in ResNet) help deep neural networks achieve high-accuracy training, which is also a way to break degeneration. We also suspect that other methods, such as batch normalization or layer normalization, assist in the training of deep neural networks, not only due to potential independence mechanisms as proposed in the original papers, such as reducing internal variance, but also at least in part because they disrupt degeneration. We all know that divisive normalization is highly effective in decorrelating the responses of hidden units, and it can also be seen as a mechanism to break degeneration.
In addition to our paper, I should also mention the recent paper by Pennington, Schoenholz, and Ganguli, “Resurrecting the sigmoid in deep learning through dynamical isometry: theory and practice.” In this paper, orthogonal initialization completely removes the degeneration problem in linear networks. They propose a method to compute the entire singular value distribution of the Jacobian matrix of nonlinear networks and show that independent of depth, a non-degenerate singular value distribution can be achieved in hard-tanh nonlinear networks (as opposed to ReLU networks). Experimental results show that networks with independent non-degenerate singular value distributions are several orders of magnitude faster than those with increasingly wider (higher variance) singular value distributions. This is compelling evidence for the importance of eliminating degeneration and controlling the entire singular value distribution of the network, rather than just the interesting comparisons made in the paper.
Paper: SKIP CONNECTIONS ELIMINATE SINGULARITIES

Paper link: https://openreview.net/pdf?id=HkwBEMWCZ
Skip connections have made training deep networks possible and have become an indispensable part of various deep neural architectures, yet there is currently no very successful and satisfactory explanation for them. In this paper, we propose a new explanation for the benefits of skip connections in training deep networks. The difficulty of training deep networks is largely caused by the singularities that arise from the model’s unidentifiability. Some of these singularities have been proven in previous work: (i) permutation symmetry in given layer nodes causes overlapping singularities, (ii) elimination causes corresponding elimination singularities, i.e., the consistency deactivation problem of nodes, and (iii) linear dependencies among nodes produce singular problems. These singularities create degenerate manifolds on the loss function surface, thus reducing learning efficiency. We believe that skip connections break the permutation symmetry of nodes, reduce the likelihood of node elimination, and decrease linear dependencies between nodes to eliminate these singularities. Furthermore, for typical initialization, skip connections remove these singularities and accelerate learning efficiency. These hypotheses have been supported by experiments on simplified models and on training deep networks on large datasets.
Original link:https://severelytheoretical.wordpress.com/2018/01/01/why-is-it-hard-to-train-deep-neural-networks-degeneracy-not-vanishing-gradients-is-the-key/
Machine Heart publishes the first AI Technology Trend Report, surveying 23 branches of artificial intelligence technology. Clarifying the historical development path, interpreting existing bottlenecks and future development trends. Clickto read the original text, and immediately obtain the full report.

