In last week’s artificial neural network course, we introduced the connection between Support Vector Machines (SVM) and feedforward networks RBF in machine learning, and the representation of adaptive linear elements (ADLINE) composed of linear functions in a single-layer network is quite similar to adaptive filters in traditional signal processing.
All of this shows that neural network algorithms seem to be able to connect with many other algorithms from different disciplines. The blog post by Matthew P. Burruss, titled Every Machine Learning Algorithm Can Be Represented as a Neural Network, further elaborates on this point.
-
Every Machine Learning Algorithm Can Be Represented as a Neural Network:https://mc.ai/every-machine-learning-algorithm-can-be-represented-as-a-neural-network-2/#:~:text=Every%20Machine%20Learning%20Algorithm%20Can%20Be%20Represented%20as,cumulated%20with%20the%20creation%20of%20the%20neural%20network.

Since the early research in the 1950s, all work in machine learning seems to have converged with the creation of neural networks. From Logistic Regression to Support Vector Machines, algorithms have emerged one after another. It is no exaggeration to say that neural networks have become the algorithm of algorithms, reaching the pinnacle of machine learning. It has also evolved from initial experimentation into a universal representation of machine learning.
In this sense, it is not just a simple algorithm, but a framework and concept that provides a broader space for building neural networks: for instance, it includes different numbers of hidden layers and nodes, various forms of activation (transfer) functions, optimization tools, loss functions, types of networks (convolutional, recurrent, etc.), and some specialized processing layers (various batch processing modes, random dropout of network parameters, etc.).
Thus, neural networks can be expanded from a fixed algorithm to a general concept, leading to the interesting assertion that any machine learning algorithm, whether a decision tree or k-nearest neighbors, can be represented using neural networks.
This concept can be validated through the following examples, and can also be rigorously proven with data.

1. Regression
First, let us define what a neural network is: it is a structure composed of an input layer, hidden layers, and an output layer, with connections between the nodes of each layer. Information is input into the network from the input layer and then passed through the hidden layers to the output layer. During the transfer process between layers, data is transformed through linear transformations (weights and biases) and nonlinear functions (activation functions). There are many algorithms to train the variable parameters in the network.
-
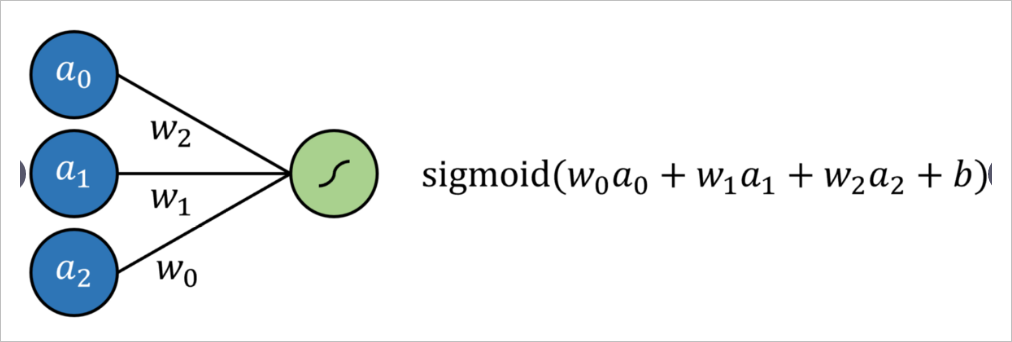
Logistic regression is simply defined as standard regression, where each input has a multiplicative coefficient and an additional offset (intercept) is added, which is then passed through the sigmoid function. This can be represented by a neural network without hidden layers, resulting in a multivariate regression with outputs in the form of sigmoid from the output neurons.
-
By replacing the output neuron activation function with a linear activation function (which can simply map the output, in other words, does nothing), linear regression is formed.
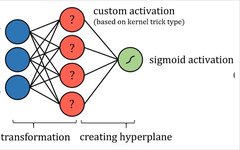
2. Support Vector Machines
The Support Vector Machine (SVM) algorithm attempts to improve the linear separability of data by projecting it into a new high-dimensional space using a so-called