Professor Zhu Jun from Tsinghua University’s Computer Science Department, leading the TSAIL team, proposed DPM-Solver (NeurIPS 2022 Oral, approximately the top 1.7%) and DPM-Solver++, which has pushed the rapid sampling algorithm of diffusion models to the extreme: achieving high-quality sampling with only 10 to 25 steps without additional training.
This year, one of the most influential advancements in the AI field is undoubtedly the explosive rise of AI image generation. Designers only need to input a textual description of an image, and AI can generate a high-resolution image of exceptional quality. Currently, the most widely used model is StabilityAI’s open-source model, Stable Diffusion, which sparked extensive discussion in the community upon its release.
However, the biggest issue with diffusion models is their extremely slow sampling speed. The model sampling starts from a pure noise image, progressively denoising it step by step until a clear image is obtained. During this process, the model must compute at least 50 to 100 steps serially to achieve a high-quality image, resulting in a generation time that is 50 to 100 times longer than other deep generative models, severely limiting the model’s deployment and practical application.
To accelerate the sampling of diffusion models, many researchers have approached from a hardware optimization perspective. For example, Google uses the JAX language to compile and run the model on TPU, while the OneFlow team [1] has achieved “one-second image generation” with their self-developed compiler for Stable Diffusion. These methods are based on the 50-step sampling algorithm PNDM[2], which experiences a significant drop in sampling quality when the number of steps is reduced.
Just a few days ago, this record was broken again! The official demo of Stable Diffusion[3] showed that the time to sample 8 images has been reduced from 8 seconds to just 4 seconds! That’s a full doubling of speed!
Moreover, the OneFlow team, based on their self-developed deep learning compiler technology, has successfully reduced the previous “one-second image generation” to “half-second image generation” without compromising sampling quality! It now takes less than 0.5 seconds on a GPU to obtain a high-definition image! Related work has been published in [1].
In fact, the core driving force behind these works comes from the DPM-Solver proposed by Professor Zhu Jun’s TSAIL team at Tsinghua University, an efficient solver specially designed for diffusion models: this algorithm requires no additional training and is applicable to both discrete and continuous-time diffusion models, achieving near convergence in 20 to 25 steps, and can obtain very high-quality sampling in just 10 to 15 steps. For Stable Diffusion, the 25-step DPM-Solver achieves better sampling quality than the 50-step PNDM, effectively doubling the sampling speed!
Project links:
-
DPM-Solver: A Fast ODE Solver for Diffusion Probabilistic Model Sampling in Around 10 Steps: https://arxiv.org/abs/2206.00927 (NeurIPS 2022 Oral)
-
DPM-Solver++: Fast Solver for Guided Sampling of Diffusion Probabilistic Models: https://arxiv.org/abs/2211.01095
-
Project open-source code: https://github.com/LuChengTHU/dpm-solver
-
Project online demo: https://huggingface.co/spaces/LuChengTHU/dpmsolver_sdm
Diffusion models define a forward process that continuously adds noise to transform an image into Gaussian noise, and then define a reverse process to progressively denoise the Gaussian noise back to a clear image for sampling:

During the sampling process, based on whether additional noise is added, diffusion models can be divided into two categories: one is the diffusion stochastic differential equation model (Diffusion SDE), and the other is the diffusion ordinary differential equation (Diffusion ODE). Both models have the same training objective function, training a “noise prediction network” by minimizing the mean square error with respect to the noise:
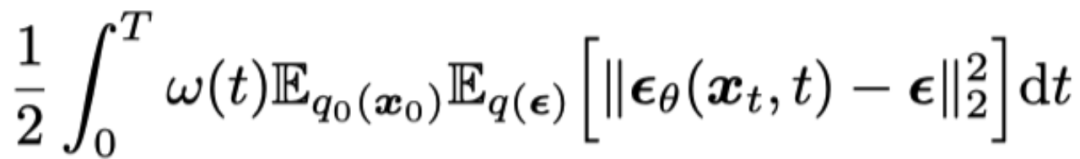
The sampling process based on Diffusion SDE can be viewed as discretizing the following stochastic differential equation:
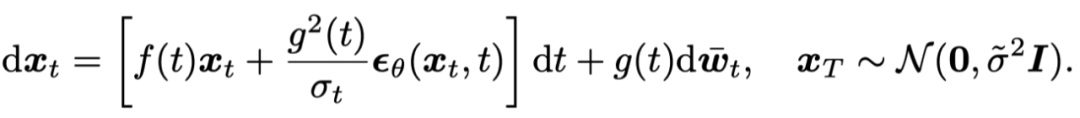
It has also been proven in [4] that DDPM[5] is a first-order discretization of the above SDE.
The sampling process based on Diffusion ODE can be viewed as discretizing the following ordinary differential equation:
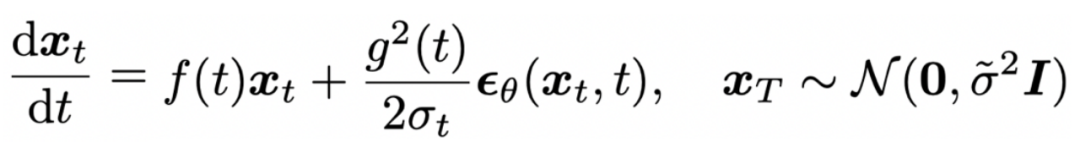
It has also been proven in [6] that DDIM[7] is a first-order discretization of the above ODE.
However, these first-order discretization methods converge very slowly, and sampling from diffusion models typically requires 100 to 1000 serial computations to obtain a high-quality image. Generally, to accelerate the sampling of diffusion models, researchers often use higher-order solvers for Diffusion ODE, such as the classic Runge-Kutta method (RK45), since ODE does not introduce additional randomness, allowing for a larger discretization step size. Given the solution at time s, the Runge-Kutta method is based on the following discretization:

This discretization treats the entire Diffusion ODE as a black box, losing the known information of the ODE, making it difficult to converge in less than 50 steps.
DPM-Solver: A Solver Designed for Diffusion Models
DPM-Solver is based on the semi-linear structure of Diffusion ODE, allowing for precise and analytical computation of the linear terms in the ODE:

The remaining integral term is a complex integral over time. However, the developers of DPM-Solver discovered that this integral can be simplified to a very simple form by making a change of variables based on log-SNR (log signal-to-noise ratio):
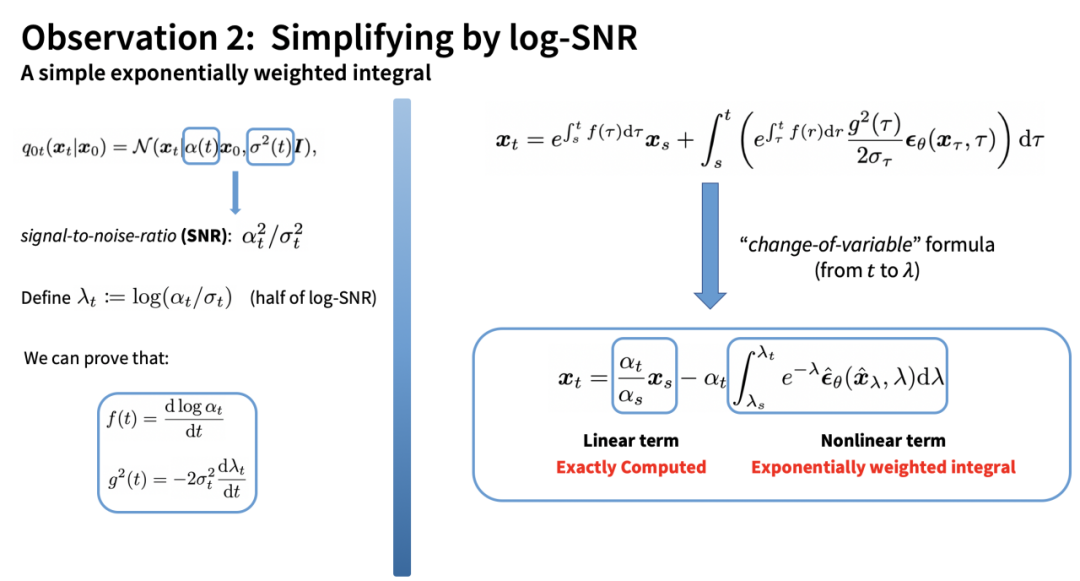
The remaining integral is an exponentially weighted integral concerning the noise prediction model. By performing a Taylor expansion on the noise prediction model, we can obtain an estimate of this integral:

This estimate contains two parts: one is the full derivative part (vector), and the other is the coefficient part (scalar). Another core contribution of DPM-Solver is that this coefficient can be computed analytically through integration by parts:
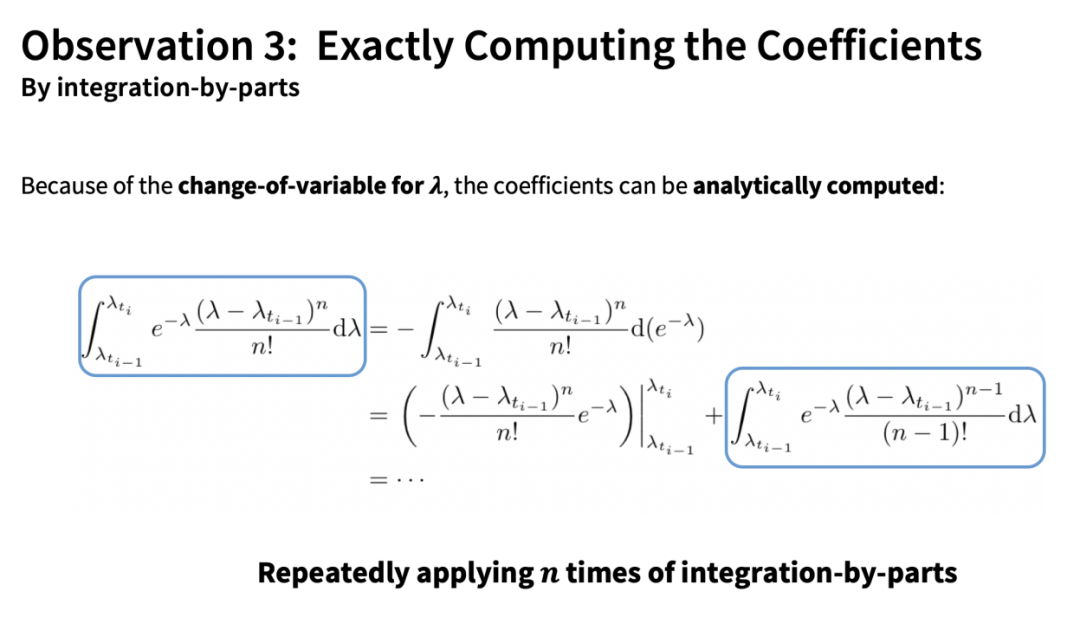
The remaining full derivative part can be approximated using numerical methods from traditional ODE solvers (without any differentiation operations):

Based on the above four points, DPM-Solver achieves the most accurate computation of all known terms while only approximating the neural network part, thus minimizing discretization errors to the greatest extent:
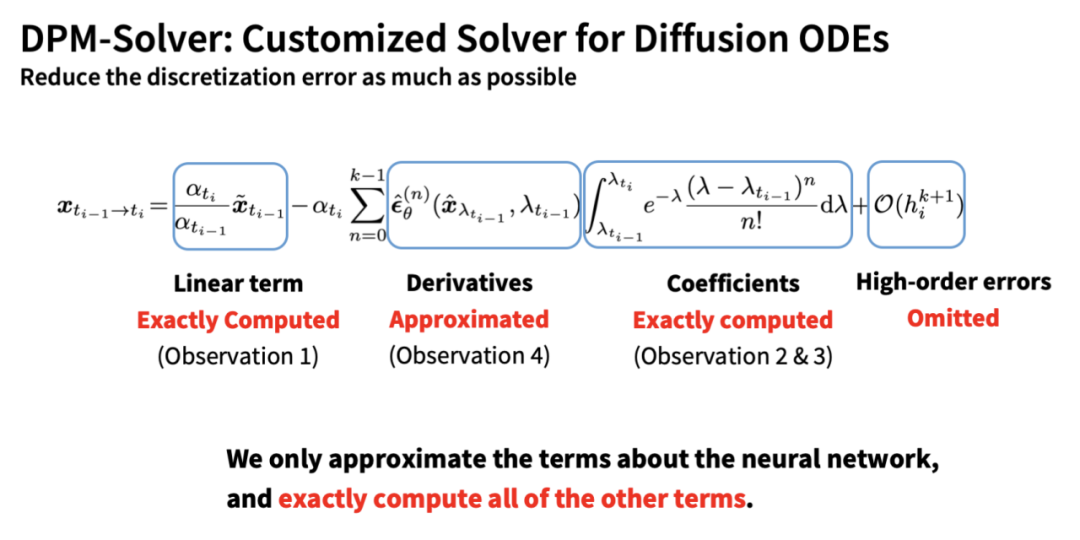
Additionally, based on this derivation, we can see that DDIM is essentially a first-order form of DPM-Solver, which also explains why DDIM can still achieve good acceleration effects with fewer steps:
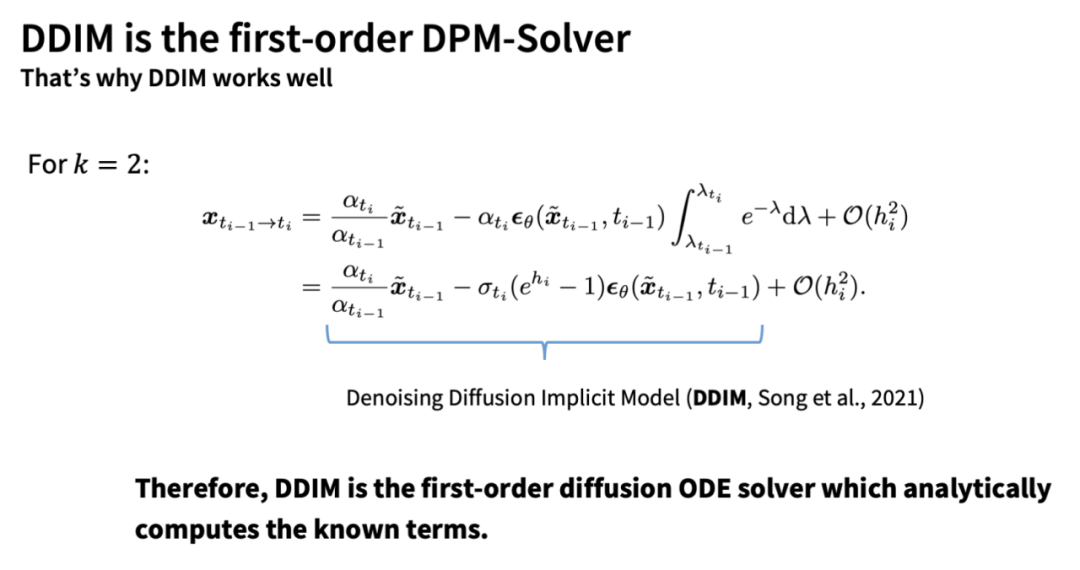
In experiments, DPM-Solver achieved acceleration effects far exceeding other sampling algorithms, converging almost completely in just 15-20 steps:
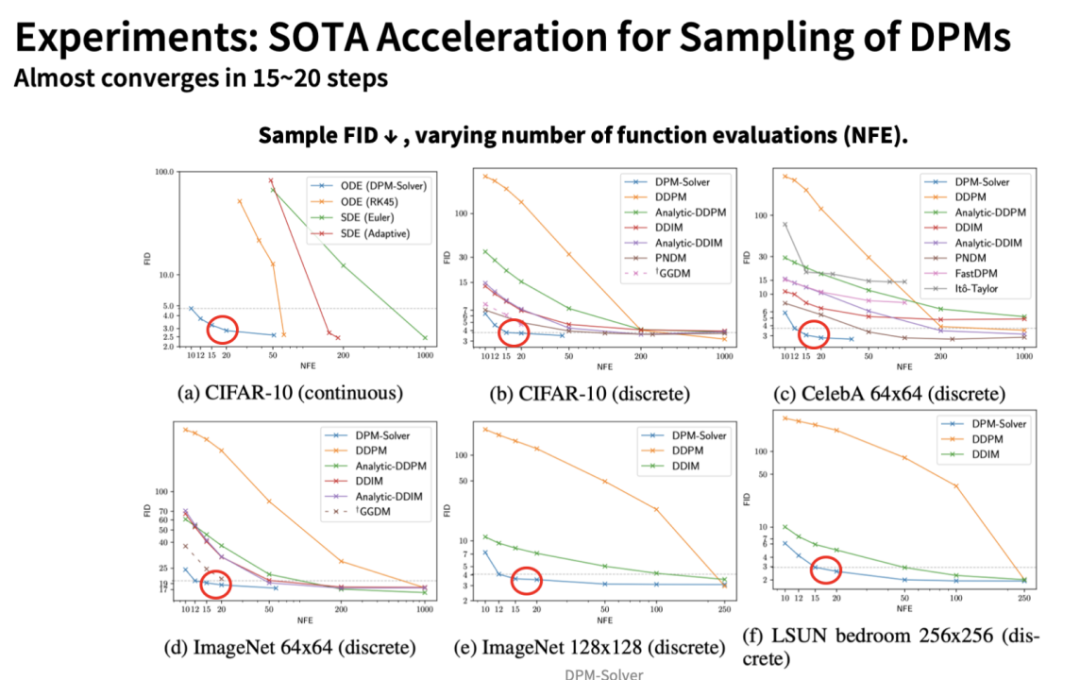
Moreover, quantitative results in the paper show that the additional computational load introduced by DPM-Solver is negligible, meaning that the acceleration effect on the number of steps is directly proportional to the acceleration effect in time—thus, with the 25-step DPM-Solver, the sampling speed of the Stable-Diffusion model effectively doubles! For example, the following figure demonstrates the effects of different sampling algorithms on Stable-Diffusion as the number of steps changes, showing that DPM-Solver can achieve very high-quality sampling with just 10 to 15 steps:

Using DPM-Solver
Using DPM-Solver is very simple, and it can be based on the official code provided by the authors or use the mainstream Diffusers library. For instance, based on the official code provided by the authors (https://github.com/LuChengTHU/dpm-solver), it only requires 3 lines:

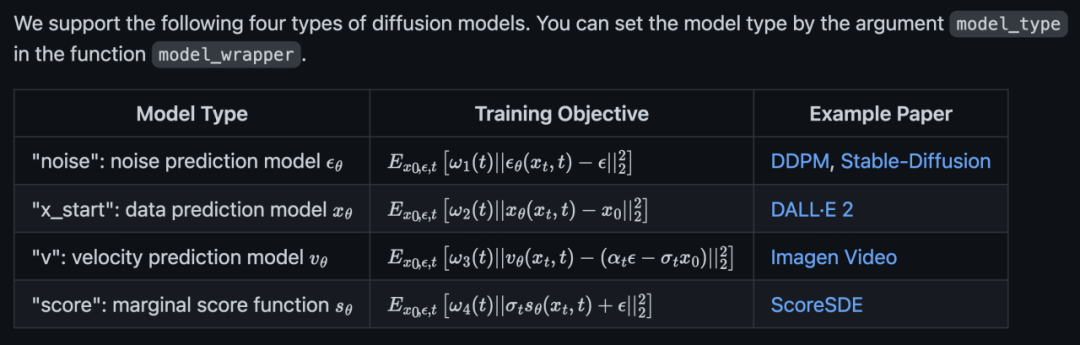
The official code supports four types of diffusion models:
It also supports unconditional sampling, classifier guidance, and classifier-free guidance:

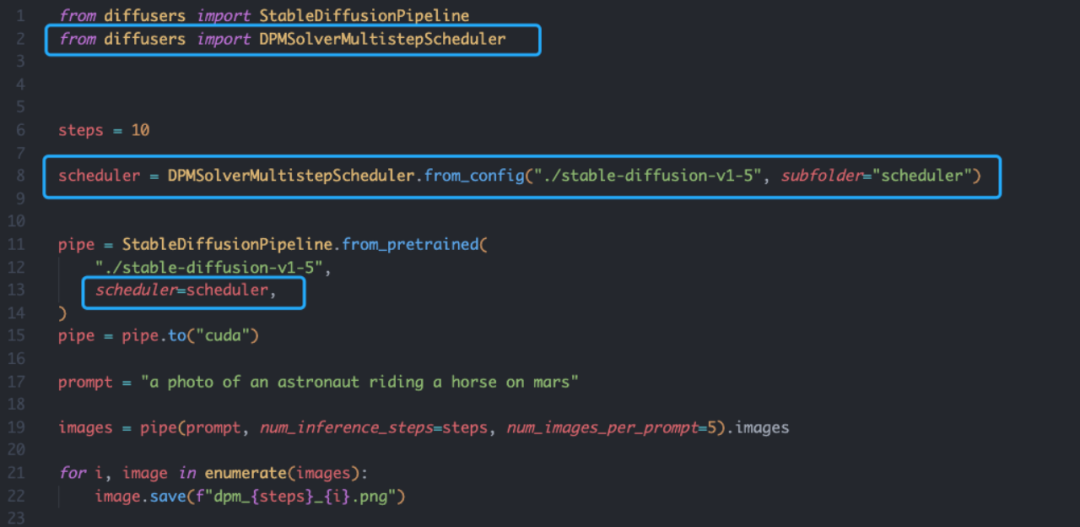
Using DPM-Solver based on the Diffusers library is also straightforward, requiring only the definition of the scheduler:
In addition, the authors’ team has also provided an online demo: https://huggingface.co/spaces/LuChengTHU/dpmsolver_sdm
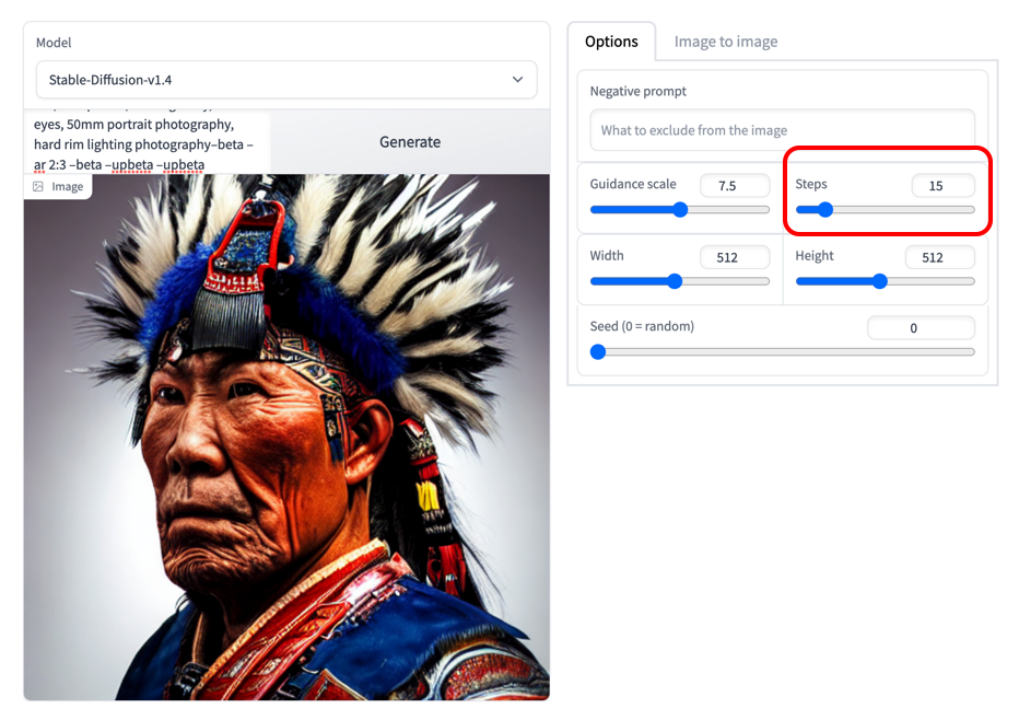
The following image is an example using 15 steps, showing that the image quality is already very high:
It is believed that with DPM-Solver, the sampling speed of diffusion models will no longer be a bottleneck.
About the Authors
The first author of the DPM-Solver paper is Dr. Lu Cheng from Tsinghua University’s TSAIL team, who also wrote an introductory article on the principles of diffusion models in a discussion on Zhihu, currently receiving over 2000 likes: https://www.zhihu.com/question/536012286/answer/2533146567
The TSAIL team at Tsinghua University has long been dedicated to theoretical and algorithmic research in Bayesian machine learning and is one of the earliest teams to study deep probabilistic generative models internationally, achieving systematic and in-depth research results in Bayesian models, efficient algorithms, and probabilistic programming libraries. Another doctoral student from the team, Bao Fan, proposed Analytic-DPM [8][9], providing a simple and surprising analytical form for the optimal mean and variance of diffusion models, winning the ICLR 2022 Outstanding Paper Award. In the field of probabilistic programming, the team released the “ZhuSuan” deep probabilistic programming library (https://zhusuan.readthedocs.io/en/latest/) [10] in 2017, being one of the earliest programming libraries aimed at deep probabilistic models. Additionally, it is worth mentioning that the two core authors of the diffusion probabilistic model, Song Yang and Song Jiaming, both conducted research training under Professor Zhu Jun’s guidance during their undergraduate studies and later went on to pursue their PhDs at Stanford University. The paper’s co-authors, Zhou Yuhao, Chen Jianfei, and Li Chongxuan, are also outstanding doctoral students trained by the TSAIL group, with Zhou Yuhao currently enrolled and Chen Jianfei and Li Chongxuan teaching at Tsinghua University’s Computer Science Department and Renmin University’s Gaoling School of Artificial Intelligence, respectively.
References:
[1] OneFlow version of Stable-Diffusion: https://github.com/Oneflow-Inc/diffusers/wiki/How-to-Run-OneFlow-Stable-Diffusion
[2] Luping Liu et al., 2022, Pseudo Numerical Methods for Diffusion Models on Manifolds, https://arxiv.org/abs/2202.09778
[3] Official demo of Stable-Diffusion: https://huggingface.co/spaces/runwayml/stable-diffusion-v1-5
[4] Yang Song et al., 2021, Score-Based Generative Modeling through Stochastic Differential Equations, https://arxiv.org/abs/2011.13456
[5] Jonathan Ho et al., 2020, Denoising Diffusion Probabilistic Models, https://arxiv.org/abs/2006.11239
[6] Tim Salimans & Jonathan Ho, 2022, Progressive Distillation for Fast Sampling of Diffusion Models, https://arxiv.org/abs/2202.00512
[7] Jiaming Song et al., 2020, Denoising Diffusion Implicit Models, https://arxiv.org/abs/2010.02502
