Source: Time Series Research
This article is approximately 3400 words long and is recommended for a 5-minute read.
This article introduces the Transformer in multivariate time series classification.
Multivariate time series classification (MTSC) has attracted extensive research attention due to its diverse real-world applications. Recently, utilizing Transformers for MTSC has achieved state-of-the-art performance. However, existing methods primarily focus on general features, providing a comprehensive understanding of the data, but they overlook category-specific features that are crucial for learning representative characteristics of each class. This leads to poor performance on datasets that are imbalanced or have overall patterns that are similar but differ in category-specific details.
To address these issues, this article presents the latest relevant research work from the University of Melbourne and Monash University, which has been accepted by KDD 2024. The researchers propose a novel Shapelet Transformer (ShapeFormer) for multivariate time series classification. It consists of two Transformer modules designed to identify category-specific features and general features in time series data. Specifically, the first module discovers category-specific features by utilizing discriminative subsequences (shapelets) extracted from the entire dataset. Meanwhile, the second Transformer module employs convolutional filters to extract general features across all categories. Experimental results show that by combining these two modules, ShapeFormer achieves top rankings in classification accuracy compared to state-of-the-art methods.
[Paper Title]
ShapeFormer: Shapelet Transformer for Multivariate Time Series Classification
[Paper URL]
https://arxiv.org/abs/2405.14608
[Paper Source Code]
https://github.com/xuanmay2701/shapeformer
Time series classification is a fundamental and crucial aspect of time series analysis. However, there are still many challenges in the research of multivariate time series classification (MTSC), especially in capturing the correlations between variables.
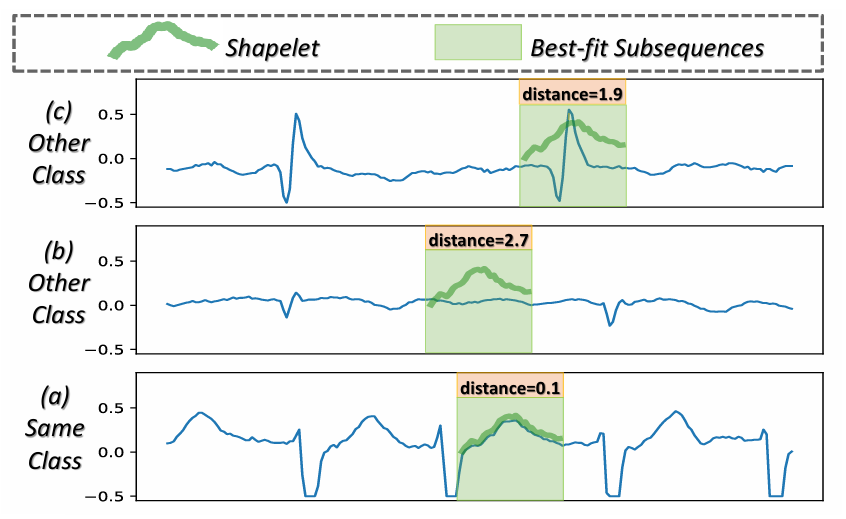
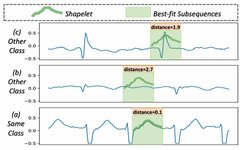
Over the past few decades, numerous researchers have introduced various methods to improve the performance of MTSC. Among them, shapelets (category-specific time series subsequences) have demonstrated their effectiveness. This success arises from the fact that each shapelet contains specific class information representing its category, and the distance between the shapelet and its category time series is much smaller than that to time series of other categories (see Figure 1). Therefore, there is increasing attention on leveraging shapelets in the MTSC field.
Figure 1: Shapelet in the Atrial Fibrillation Dataset
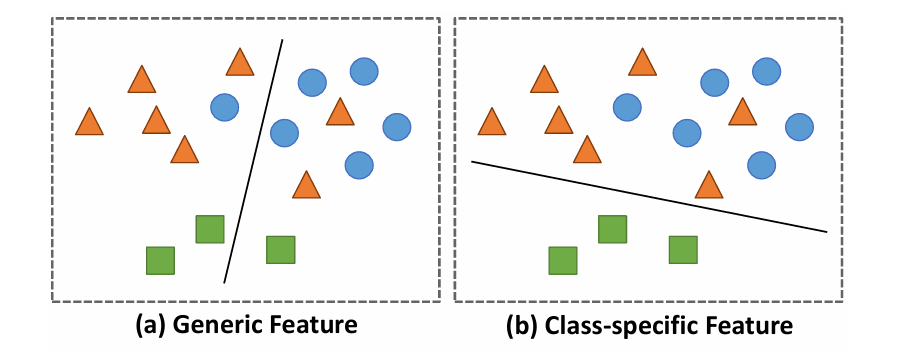
Clearly, Transformers used in multivariate time series classification (MTSC) have demonstrated state-of-the-art (SOTA) performance. Existing methods only extract general features from timestamps or common subsequences in the time series as input to the Transformer model to capture correlations between them. These features only contain general characteristics of the time series, providing a broad understanding of the data. However, they overlook the essential category-specific features necessary for the model to capture representative characteristics of each class.
As a result, the model performs poorly in the following two scenarios:
-
Instances in the dataset are very similar in overall patterns, differing only in minor category-specific patterns, and effective classification cannot be achieved using only general features;
-
Imbalanced datasets where general features focus only on classifying the majority of categories while neglecting the minority categories.
Figure 2: Separation hyperplanes using (a) general features have higher overall accuracy, while using (b) category-specific features performs better in classifying individual categories.
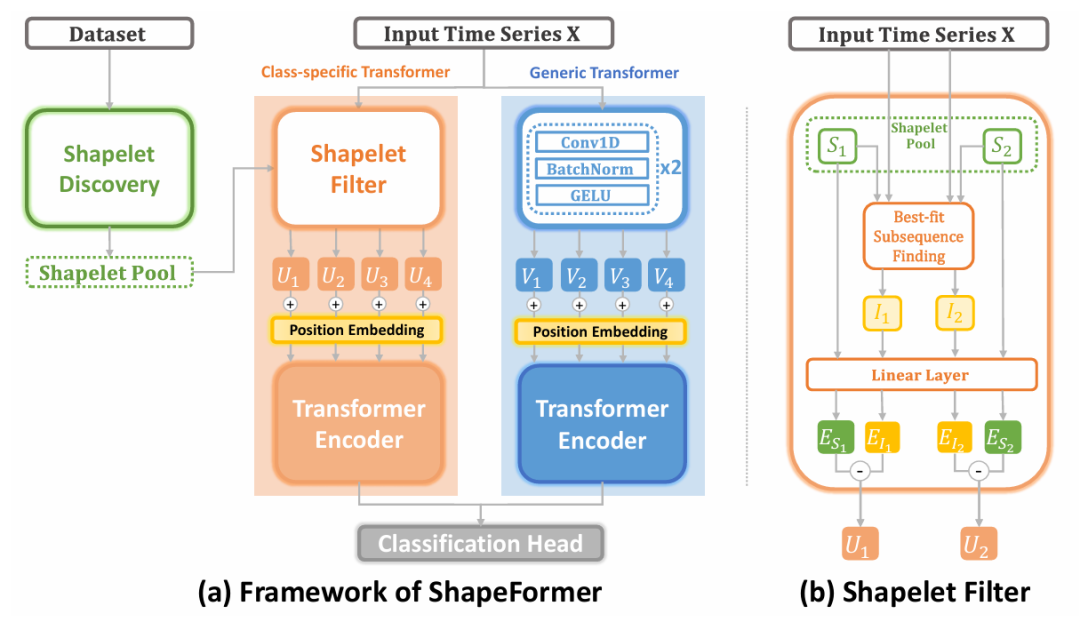
ShapeFormer is a Transformer-based method that combines the advantages of category-specific features and general features in time series. Compared to existing Transformer-based MTSC methods, ShapeFormer first extracts shapelets from the training dataset, and then for a given input time series, it processes it through two Transformer modules, including a category-specific shapelet Transformer and a general convolutional Transformer. The outputs of these two modules are then concatenated and fed into the final classification head.
Figure 3: Overall Architecture of ShapeFormer
The researchers introduced an Offline Shapelet Discovery (OSD) method to extract shapelets from the training dataset of multivariate time series. Compared to other methods, OSD uses Perceptually Important Points (PIPs) to compress the time series data by selecting points that closely mimic the original data, thereby efficiently selecting high-quality shapelets. The selection process is based on reconstruction distance, and the highest index is continuously selected. The reconstruction distance is defined as the perpendicular distance between the target point and the line reconstructed by the two most recently chosen important points.
This method consists of two main stages: shapelet extraction and shapelet selection.
In the first stage, OSD first extracts shapelet candidates by identifying PIPs; in the second stage, the same number of shapelets is selected for each category.
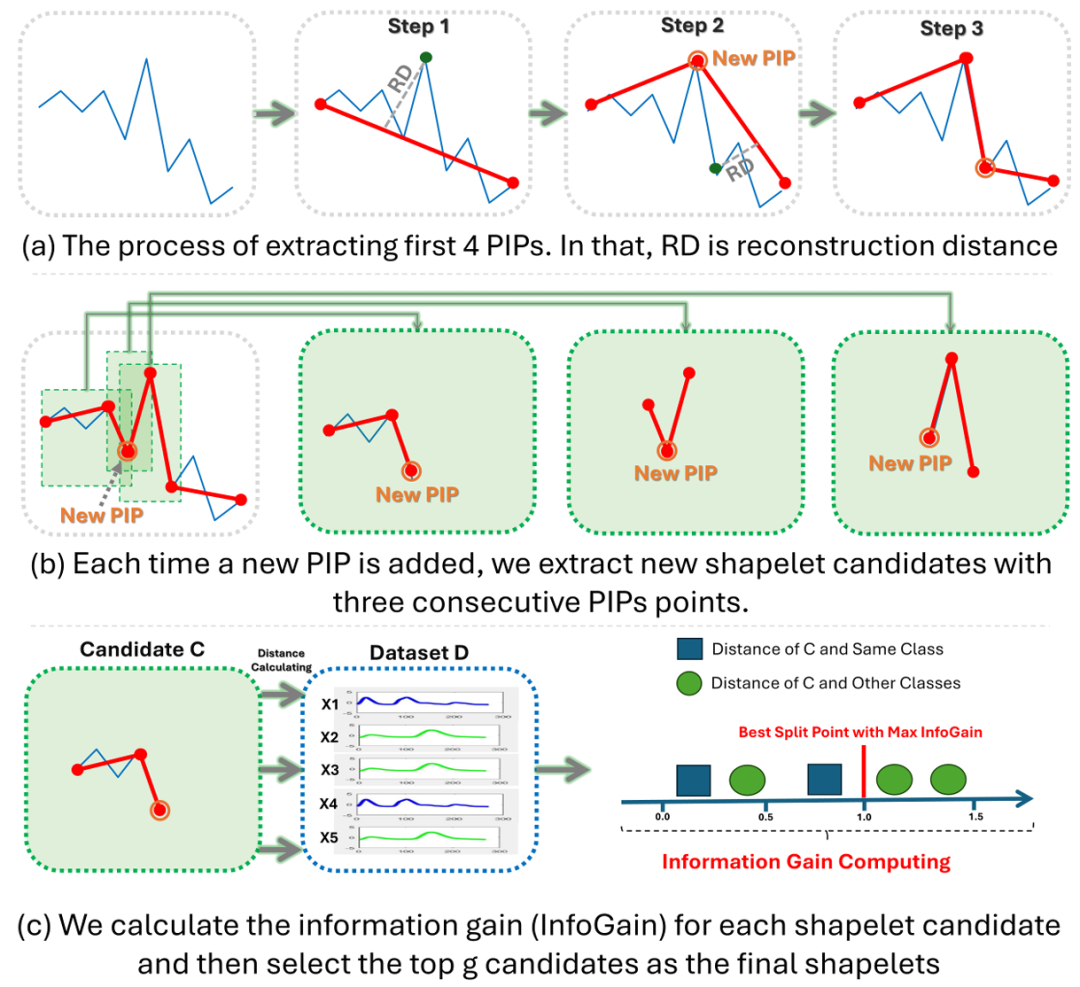 Figure 4: Process of Offline Shapelet Discovery
02 Category-Specific Transformer
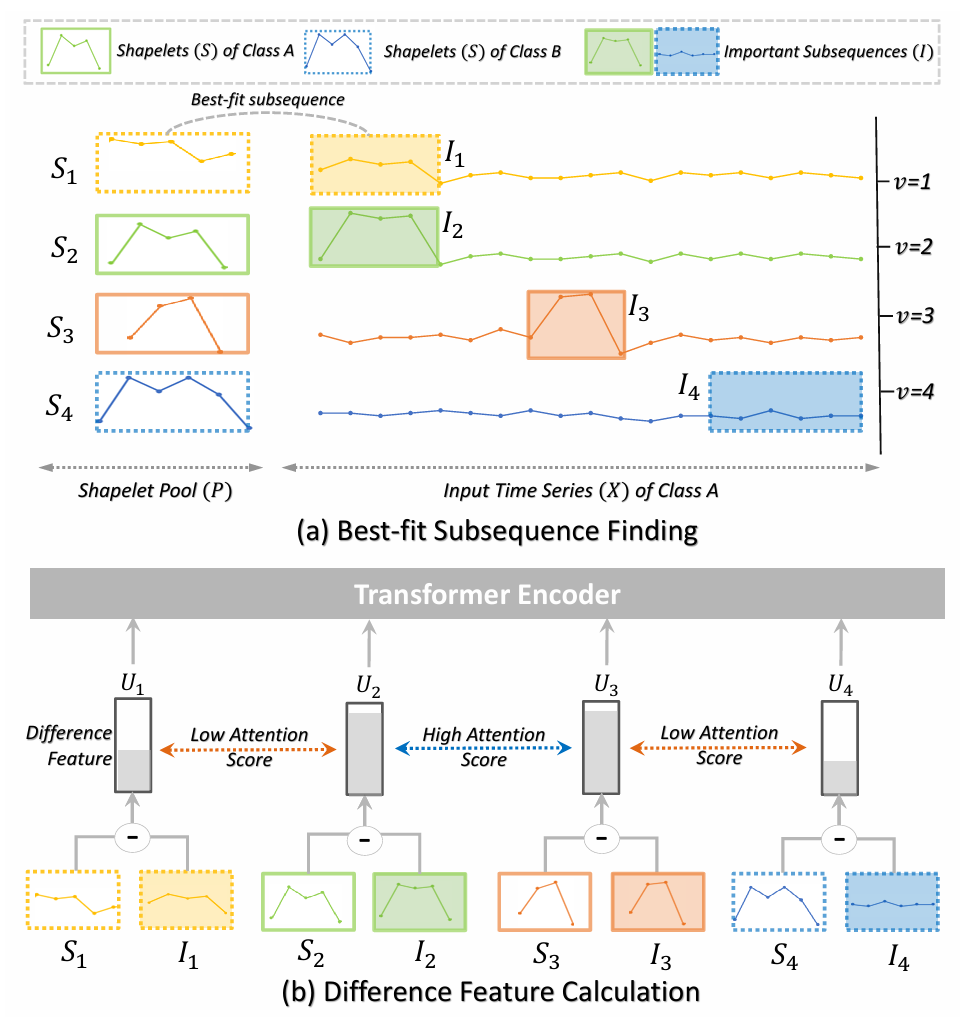
Shapelet Filter. To leverage the category-specific characteristics of shapelets, the researchers proposed a Shapelet Filter that effectively discovers input labels for the Transformer model and finds subsequences in the input time series that match the shapelets most closely (as shown in Figure 5a). To reduce computation time and effectively utilize the positional information of shapelets, the researchers proposed limiting the search for the best-matching subsequence to the neighboring region within a hyperparameter window size 𝑤 around the actual position of the shapelet.
Figure 5: (a) Method for finding the best-matching subsequence; (b) Method for calculating differential features
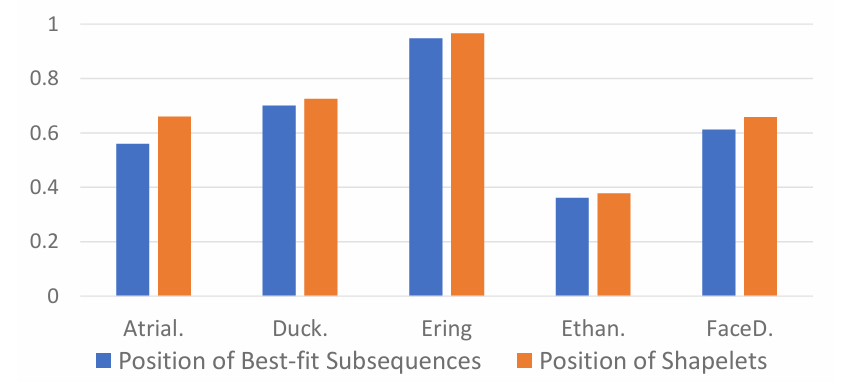
Positional Embedding. To better indicate the positional information of shapelets, three types of positional embeddings are considered: starting index, ending index, and variable. Specifically, the researchers recommend using one-hot vector representations of these indices and then using a linear projector to learn their embeddings. Performance improves when using the position of shapelets rather than the positions of the best-matching subsequences. This improvement can be attributed to the fixed position being easier to learn than the unstable positions of the best-matching subsequences.
Transformer Encoder. The category-specific differential features and their corresponding positional embeddings are input into the Transformer encoder to learn the correlations between them. Since these features have category-representative characteristics, the attention scores for features within the same category are enhanced compared to features from different categories. This enhancement helps the model better distinguish between different categories. Additionally, due to the nature of shapelets, the differential features have the capability to identify significant subsequences across different time positions and variables in the time series. This capability enables the module to effectively capture temporal and variable dependencies in time series data.
Category Label. The first differential feature with the highest information gain from the shapelet is used as the category label for final classification. The reason for this is that averaging over all labels loses information about different features 𝑈𝑖. Furthermore, the first label carrying the highest information gain contains the most important feature for effectively classifying time series.
The general Transformer utilizes convolutional filters to extract general features from the time series. Specifically, the researchers employed two CNN components, each containing Conv1D, BatchNorm, and GELU, to effectively discover general features. The first block aims to capture temporal patterns in the time series using Conv1D filters ∈R^(1×𝑑𝑐). On the other hand, the second block uses Conv1D filters ∈R^(𝑉×1) to capture correlations between variables in the time series.
Subsequently, these features are fed into multi-head attention heads to learn correlations. Each attention head has the ability to capture different patterns in the time series data.
In terms of datasets, the researchers used 30 different multivariate time series classification datasets from the UEA archive, covering multiple domains such as human activity recognition, motion classification, and ECG classification.
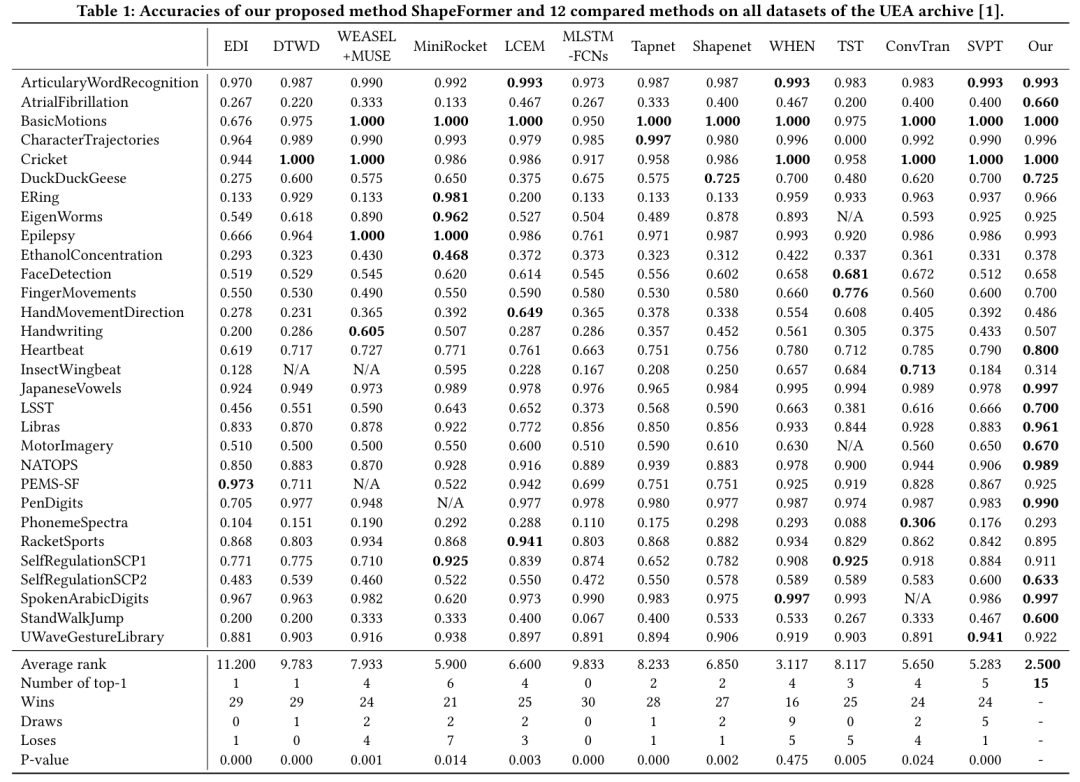
Table 1 shows the accuracy comparison results of ShapeFormer with other methods on the UEA datasets, demonstrating that ShapeFormer achieves the best performance across multiple datasets and excels in both average ranking and top-1 counts. ShapeFormer can be considered the latest technical level (SOTA) in the field of MTSC.
Table 1: Accuracy of ShapeFormer Method Compared to 12 Comparison Methods on All Datasets of the UEA Archive
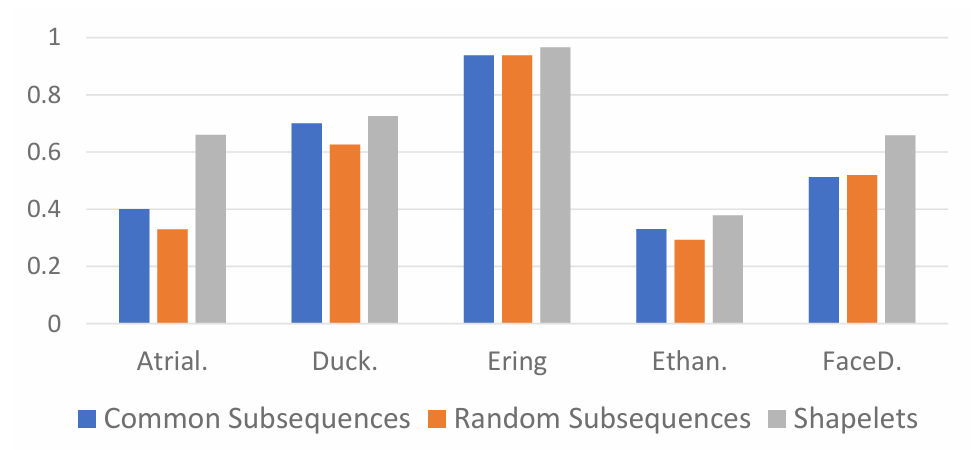
Regarding the effectiveness of using shapelets, the researchers compared the performance when using random subsequences, such as general subsequences and shapelets in this method. The results indicate that shapelets outperform the other two methods in terms of accuracy across all five datasets. This highlights the advantage of high-discriminative shapelet features in improving the performance of Transformer-based models.
Figure 6: Accuracy using shapelets and the other two types of subsequences
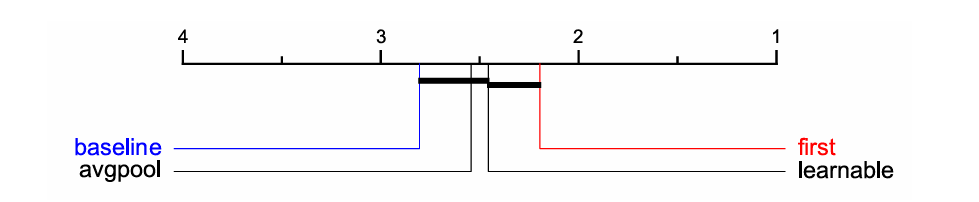
Figure 7: Average ranking of three variants of ShapeFormer compared to the baseline (SVP-T[50] — the current SOTA method based on Transformer)
Figure 8: Accuracy using positions of best-fitting subsequences and shapelets
Figure 9: Average accuracy ranking of different differential feature calculation methods
Figure 10: Average accuracy ranking of different category label designs
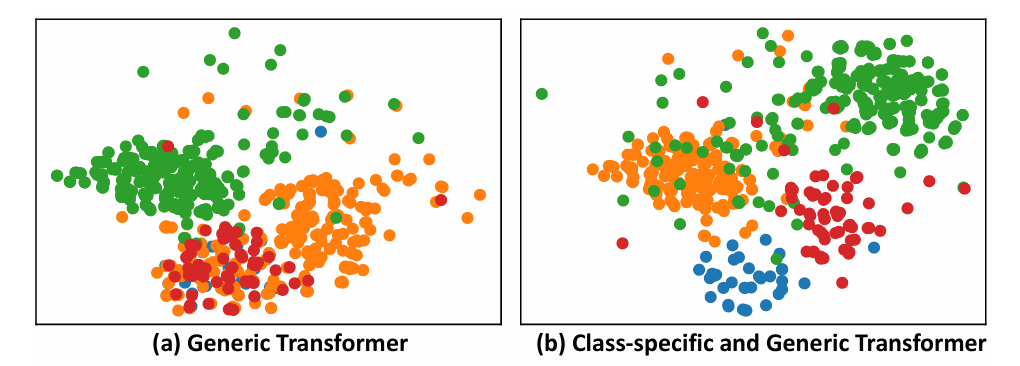
To illustrate the effectiveness of combining category-specific and general feature Transformer modules for classifying imbalanced data, the researchers conducted experiments on the LSST dataset. The LSST dataset contains 16 categories, and the experiment randomly selected 4 categories, represented in blue, orange, green, and red. Clearly, the sample sizes of the blue and red categories are significantly smaller compared to the green and orange categories. Figure 11(a) shows that the general Transformer prioritizes the majority classes (green and orange) but neglects the minority classes (blue and red). However, in Figure 11(b), the combination of the category-specific Transformer and the general Transformer effectively distinguishes all four categories.
Figure 11: t-SNE visualization of 4 categories in the LSST dataset using (a) general Transformer and (b) combination of category-specific and general Transformers
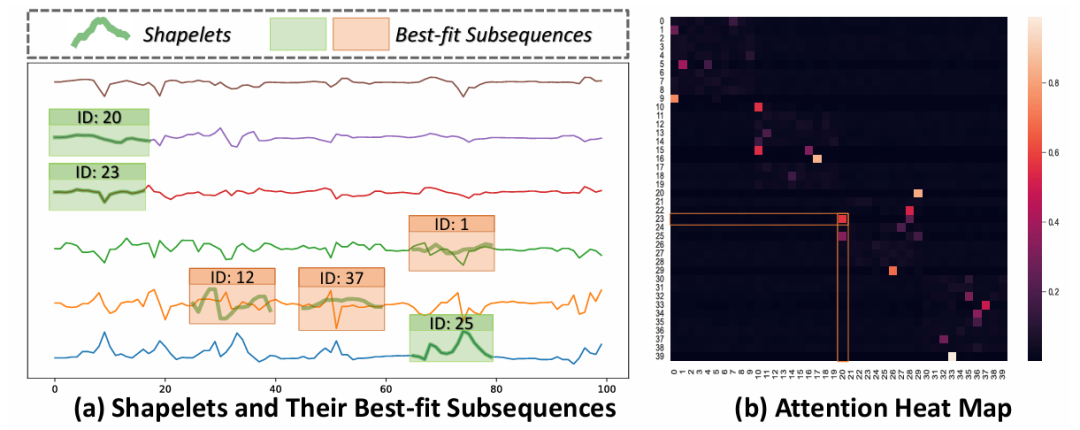
To interpret the results of ShapeFormer, the researchers used the BasicMotions dataset from the UEA archive, focusing on human activity recognition with 4 categories (badminton, standing, walking, and running). Figure 12(a) highlights the ability of ShapeFormer to identify key subsequences at different positions and variables in the time series. Additionally, shapelets belonging to the same “walking” category tend to have higher similarity to the best-fitting subsequences than to shapelets from other categories. Figure 12(b) reveals that shapelets within the same category generally receive higher attention scores. This enhanced attention allows the model to focus more on the correlations between shapelets within the same category, thereby improving overall performance.
Figure 12: (a) The green box outlines the top three shapelets; the orange box shows three random shapelets extracted from the “walking” category of a random input time series from the BasicMotions dataset from other categories. (b) Attention heatmap of all shapelets.
In future work, the researchers plan to leverage the powerful capabilities of shapelets in various time series analysis tasks, such as prediction or anomaly detection.
Figure 4: Process of Offline Shapelet Discovery
02 Category-Specific Transformer
Shapelet Filter. To leverage the category-specific characteristics of shapelets, the researchers proposed a Shapelet Filter that effectively discovers input labels for the Transformer model and finds subsequences in the input time series that match the shapelets most closely (as shown in Figure 5a). To reduce computation time and effectively utilize the positional information of shapelets, the researchers proposed limiting the search for the best-matching subsequence to the neighboring region within a hyperparameter window size 𝑤 around the actual position of the shapelet.
Figure 5: (a) Method for finding the best-matching subsequence; (b) Method for calculating differential features
Positional Embedding. To better indicate the positional information of shapelets, three types of positional embeddings are considered: starting index, ending index, and variable. Specifically, the researchers recommend using one-hot vector representations of these indices and then using a linear projector to learn their embeddings. Performance improves when using the position of shapelets rather than the positions of the best-matching subsequences. This improvement can be attributed to the fixed position being easier to learn than the unstable positions of the best-matching subsequences.
Transformer Encoder. The category-specific differential features and their corresponding positional embeddings are input into the Transformer encoder to learn the correlations between them. Since these features have category-representative characteristics, the attention scores for features within the same category are enhanced compared to features from different categories. This enhancement helps the model better distinguish between different categories. Additionally, due to the nature of shapelets, the differential features have the capability to identify significant subsequences across different time positions and variables in the time series. This capability enables the module to effectively capture temporal and variable dependencies in time series data.
Category Label. The first differential feature with the highest information gain from the shapelet is used as the category label for final classification. The reason for this is that averaging over all labels loses information about different features 𝑈𝑖. Furthermore, the first label carrying the highest information gain contains the most important feature for effectively classifying time series.
The general Transformer utilizes convolutional filters to extract general features from the time series. Specifically, the researchers employed two CNN components, each containing Conv1D, BatchNorm, and GELU, to effectively discover general features. The first block aims to capture temporal patterns in the time series using Conv1D filters ∈R^(1×𝑑𝑐). On the other hand, the second block uses Conv1D filters ∈R^(𝑉×1) to capture correlations between variables in the time series.
Subsequently, these features are fed into multi-head attention heads to learn correlations. Each attention head has the ability to capture different patterns in the time series data.
In terms of datasets, the researchers used 30 different multivariate time series classification datasets from the UEA archive, covering multiple domains such as human activity recognition, motion classification, and ECG classification.
Table 1 shows the accuracy comparison results of ShapeFormer with other methods on the UEA datasets, demonstrating that ShapeFormer achieves the best performance across multiple datasets and excels in both average ranking and top-1 counts. ShapeFormer can be considered the latest technical level (SOTA) in the field of MTSC.
Table 1: Accuracy of ShapeFormer Method Compared to 12 Comparison Methods on All Datasets of the UEA Archive
Regarding the effectiveness of using shapelets, the researchers compared the performance when using random subsequences, such as general subsequences and shapelets in this method. The results indicate that shapelets outperform the other two methods in terms of accuracy across all five datasets. This highlights the advantage of high-discriminative shapelet features in improving the performance of Transformer-based models.
Figure 6: Accuracy using shapelets and the other two types of subsequences
Figure 7: Average ranking of three variants of ShapeFormer compared to the baseline (SVP-T[50] — the current SOTA method based on Transformer)
Figure 8: Accuracy using positions of best-fitting subsequences and shapelets
Figure 9: Average accuracy ranking of different differential feature calculation methods
Figure 10: Average accuracy ranking of different category label designs
To illustrate the effectiveness of combining category-specific and general feature Transformer modules for classifying imbalanced data, the researchers conducted experiments on the LSST dataset. The LSST dataset contains 16 categories, and the experiment randomly selected 4 categories, represented in blue, orange, green, and red. Clearly, the sample sizes of the blue and red categories are significantly smaller compared to the green and orange categories. Figure 11(a) shows that the general Transformer prioritizes the majority classes (green and orange) but neglects the minority classes (blue and red). However, in Figure 11(b), the combination of the category-specific Transformer and the general Transformer effectively distinguishes all four categories.
Figure 11: t-SNE visualization of 4 categories in the LSST dataset using (a) general Transformer and (b) combination of category-specific and general Transformers
To interpret the results of ShapeFormer, the researchers used the BasicMotions dataset from the UEA archive, focusing on human activity recognition with 4 categories (badminton, standing, walking, and running). Figure 12(a) highlights the ability of ShapeFormer to identify key subsequences at different positions and variables in the time series. Additionally, shapelets belonging to the same “walking” category tend to have higher similarity to the best-fitting subsequences than to shapelets from other categories. Figure 12(b) reveals that shapelets within the same category generally receive higher attention scores. This enhanced attention allows the model to focus more on the correlations between shapelets within the same category, thereby improving overall performance.
Figure 12: (a) The green box outlines the top three shapelets; the orange box shows three random shapelets extracted from the “walking” category of a random input time series from the BasicMotions dataset from other categories. (b) Attention heatmap of all shapelets.
In future work, the researchers plan to leverage the powerful capabilities of shapelets in various time series analysis tasks, such as prediction or anomaly detection.
Data Science THU, as a public account focused on data science, is backed by the Tsinghua University Big Data Research Center, sharing cutting-edge research dynamics in data science and big data technology innovation, continuously disseminating knowledge in data science, striving to build a platform for data talent aggregation, and creating the strongest group of big data in China.

Sina Weibo: @Data Science THU
WeChat Video Account: Data Science THU
Today’s Headlines: Data Science THU