Selected from arXiv
Authors: Matthew MacKay et al.
Translated by: Machine Heart
Contributors: Gao Xuan, Zhang Qian
Recurrent Neural Networks (RNNs) achieve the best current performance in processing sequential data, but they require a large amount of memory during training. Reversible Recurrent Neural Networks provide a way to reduce the memory requirements for training, as hidden states do not need to be stored but can be recalculated during backpropagation. This paper first shows that fully reversible RNNs, which do not need to store hidden activations, are fundamentally limited because they cannot forget information in the hidden states. Then, the researchers provide a scheme to store a small number of bits to achieve complete reversal of forgotten information. The method presented in this paper achieves performance comparable to traditional models while requiring only 1/10 to 1/15 of the memory needed by traditional models.
Recurrent Neural Networks (RNNs) have achieved excellent performance on various tasks such as speech recognition [1], language modeling [2,3], and machine translation [4,5]. However, training RNNs requires a large amount of memory. The standard training algorithm is Truncated Backpropagation Through Time (TBPTT) [6,7]. This algorithm divides input sequences into shorter subsequences T, processes each subsequence, and backpropagates the gradients. If the size of the model’s hidden state is H, then the memory required for TBPTT is O(T H).
Reducing the memory requirements of the TBPTT algorithm increases the length T of the truncated sequences, thereby capturing correlations over longer time scales. It can also increase the size H of the hidden states or utilize deeper transformations from input to hidden, hidden to hidden, or hidden to output, thereby giving the model stronger expressive power. Increasing the depth of these transformations can improve the performance of polyphonic music prediction, language modeling, and neural machine translation (NMT) [8,9,10].
The reversible network architecture provides a method to reduce the memory requirements of TBPTT. The reversible architecture allows for the reconstruction of the hidden state at the current time step given the next hidden state and the current input, enabling TBPTT to be performed without storing hidden states at each time step. The cost is an increase in computational cost to reconstruct the hidden states during backpropagation.
This paper first introduces reversible architectures similar to the widely used Gated Recurrent Unit (GRU) [11] and Long Short-Term Memory (LSTM) [12] architectures. It then demonstrates that any fully reversible RNN that does not need to store hidden activations will fail on a simple one-step prediction task. Even though this task is simple for ordinary RNNs, it fails in fully reversible models because they need to remember the input sequence to complete the task. Based on this finding, the researchers extend the efficient memory inversion method by Maclaurin et al. [13] to store a small number of bits in each unit to fully reverse the forgotten information in the architecture.
The researchers evaluated the performance of these models on language modeling and neural machine translation benchmarks. Depending on the task, dataset, and chosen architecture, the reversible models (without attention mechanisms) require only 1/10 to 1/15 of the memory needed by traditional models. The reversible models achieved performance comparable to traditional LSTM and GRU models on the word-level language modeling task on the Penn TreeBank dataset [14], falling behind traditional models by 2-5 points in perplexity on the WikiText-2 dataset [15].
Using attention-based recurrent sequence-to-sequence models to save memory is challenging because the hidden states of the encoder must be stored in memory simultaneously to execute the attention mechanism. Performing the attention mechanism on a subset of hidden states connected to the embedded words can solve this problem. After using this technique, the reversible models achieved success in neural machine translation tasks, outperforming baseline GRU and LSTM models on the Multi30K dataset [16] and achieving competitive performance on the IWSLT 2016 [17] benchmark. This technique can reduce memory in the decoder to 1/10-1/15 of the original and in the encoder to 1/5-1/10 of the original.
Paper: Reversible Recurrent Neural Networks

Paper link: https://arxiv.org/pdf/1810.10999v1.pdf
Abstract: Recurrent Neural Networks (RNNs) achieve the best current performance in processing sequential data, but they require a large amount of memory during training, limiting the flexibility of trainable RNN models. Reversible RNN-RNN can perform hidden state to hidden state transformations, providing a path to reduce training memory requirements, as hidden states do not need to be stored but can be recalculated during backpropagation. We first show that fully reversible RNNs that do not need to store hidden activations are fundamentally limited because they cannot forget information in the hidden states. We then provide a scheme to store a small number of bits to achieve complete reversal of forgotten information. Our method achieves performance comparable to traditional models while reducing activation memory overhead to 1/10-1/15 of the original. We then extend the technique to attention-based sequence-to-sequence models, where performance remains unchanged, but reduces memory overhead in the decoder to 1/10-1/15 of the original and in the encoder to 1/5-1/10 of the original.
3 Reversible Recurrent Architectures
The techniques for constructing RevNets can be combined with traditional RNN models to generate reversible RNNs. In this section, we propose reversible architectures similar to GRU and LSTM.
3.1 Reversible GRU
We first review the GRU equations for calculating the next hidden state h^(t+1) given the current hidden state h^(t) and current input x^(t) (biases omitted):
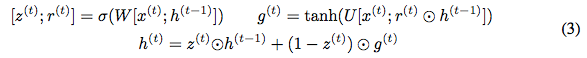
The ⊙ in the equation indicates element-wise multiplication. To make the updates reversible, we split the hidden state h into two groups, h = [h_1; h_2]. We update these groups using the following rules:
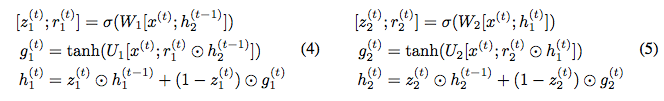
Note that h_1^(t) and non-h_1^(t-1) are used to compute the updates for h_2^(t). We call this model the Reversible Gated Recurrent Unit or RevGRU.
3.2 Reversible LSTM
Next, we construct a reversible LSTM. This LSTM separates the hidden state into output state h and cell state c, with the update equations:
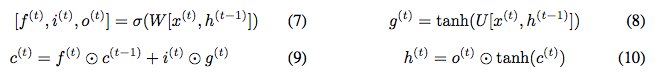
We cannot directly use our reversible method because the update of h^(t) is not a non-linear transformation of h^(t-1). Nevertheless, reversibility can be achieved by using the following equation:
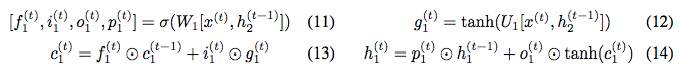
We use c_1^(t) and h_1^(t) to compute the updates for c_2 and h_2 in the same way as the above equation. We call this model the Reversible LSTM or RevLSTM.
3.3 Reversibility of Finite Precision Algorithms
We have defined reversible RNNs in precise algorithms. However, in practice, due to limited numerical precision, hidden states cannot be completely reconstructed. Considering the RevGRU equations 4 and 5, if the hidden state h is stored in fixed-point, multiplying h by z (whose entries are less than 1) will destroy information, preventing complete reconstruction. For example, multiplying hidden units by 1/2 is equivalent to discarding the least significant byte, which cannot be recovered in backpropagation. These errors in information loss accumulate exponentially over time steps, leading to the initial hidden state obtained through inversion being far from the true initial state. The same problem also affects the reconstruction of hidden states in RevLSTM. Therefore, we find that forgetting is the main obstacle to constructing fully reversible recurrent architectures.
There are two feasible approaches to solving this problem. The first is to remove the forgetting step. For RevGRU, this means we compute z_i^(t), r_i^(t), and g_i^(t) as before, and update h_i^(t) using:
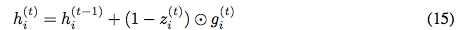
We call this model the No-Forgetting RevGRU or NF-RevGRU. Because NF-RevGRU’s updates do not discard information, we only need to store one hidden state in memory during training at any given time. A similar approach can be used to define NF-RevLSTM.
The second method is to accept some memory usage and store the information forgotten from the hidden state during forward computation. We can then restore this information to the hidden state during backpropagation to achieve complete reconstruction. The specifics will be discussed in section 5.
4 Impossibility of No Forgetting
We have shown that if no information is discarded, a reversible RNN with finite precision can be constructed. We cannot find an architecture that achieves ideal performance on tasks such as language modeling. This is consistent with previous findings that forgetting is crucial for LSTM performance [23,24]. In this section, we argue that this is due to a fundamental limitation of non-forgetting reversible models: if no hidden state can be forgotten, then the hidden state at any given time step must contain enough information to reconstruct all previous hidden states. Therefore, any information stored in the hidden state at one time step must be retained in all future time steps to ensure precise reconstruction, which exceeds the model’s storage capacity.
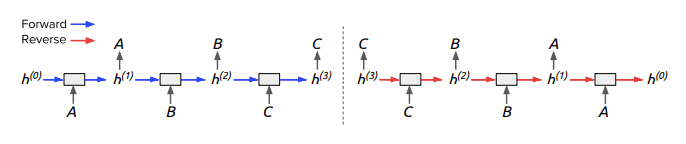
Figure 1: Expanding the backpropagation of a fully reversible model on a repetitive task to obtain sequence-to-sequence computation. Left: the repetitive task itself, the model repeats each input instruction. Right: the expanded inversion. The model effectively uses the final hidden state to reconstruct all input instructions, meaning the entire input sequence must be stored in the final hidden state.
5 Reversibility of Forgetting
Since zero forgetting is impossible, we must explore the second scheme for achieving reversibility: storing the information lost from the hidden state during forward computation and restoring it during backpropagation. Initially, we examined discrete forgetting that allows forgetting only an integer bit. This leads to: if n bits are forgotten during forward propagation, we can store these n bits in a stack and restore them to the hidden state during reconstruction. However, limiting our model to forget only integer bits results in a significant drop in performance compared to baseline models. The following content of this paper will focus on partial forgetting, where only a small portion of bits are forgotten.
5.2 Memory Savings Under Attention Mechanism
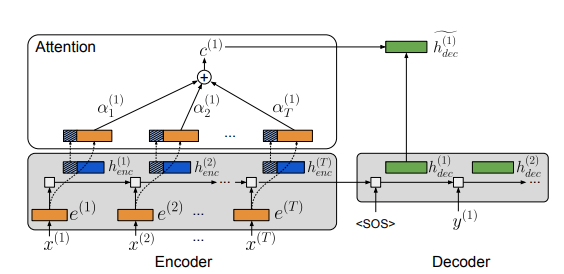
Figure 2: Attention mechanism in NMT. Word embeddings, encoder hidden states, and decoder hidden states are represented in orange, blue, and green respectively; the striped area of the encoder hidden states represents the portion stored in memory by the attention mechanism. The last few vectors used to compute the context vector connect the word embeddings and encoder hidden states.
6 Experiments

Table 1: Validation perplexity on Penn TreeBank word-level language modeling (memory savings). Under no constraints, the results show for each hidden unit per time step when forgetting is limited to 2 bits, 3 bits, and 5 bits.
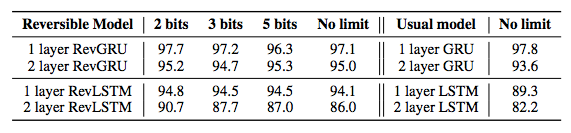
Table 2: Validation perplexity on WikiText-2 word-level language modeling. Under no constraints, the results show for each hidden unit per time step when forgetting is limited to 2 bits, 3 bits, and 5 bits.
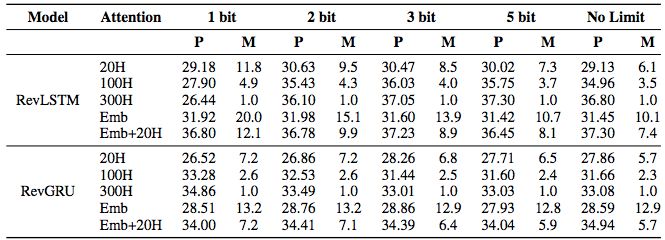
Table 3: Performance of the Multi30K dataset under different forgetting constraints. P is the test BLEU score; M indicates the average memory saved by the encoder during training.
This article is translated by Machine Heart, please contact this public account for authorization to reprint.
✄————————————————
Join Machine Heart (full-time reporter/intern): [email protected]
Submissions or inquiries for reports: content@jiqizhixin.com
Advertising & Business Cooperation: [email protected]
