Qwen Series Technical Interpretation 3 - Architecture

Shadows slant across the shallow water, a faint fragrance drifts in the moonlight at dusk. Hello everyone, I am the little girl selling hot dry noodles. I am very happy to share cutting-edge technology and thoughts in the field of artificial intelligence with my friends.

Following the previous shares in the same series: Qwen Series Technology Overview 1 – The Evolution of Qwen、 Qwen Series Technical Interpretation 2 – Data. Today, I will share the model structure used in Qwen, mainly involving the network architecture of dense models and MoE models.

Key Innovations

1. Dense Model Architecture

RoPE Rotary Positional Encoding: Enhances the expressiveness of positional information.
SwiGLU Activation Function: Improves the model’s non-linear expressive capabilities.
RMSNorm Normalization: Simplifies the computation process and improves numerical stability.
Grouped Query Attention (GQA): Optimizes the use of KV cache during inference, significantly increasing throughput.
Dual Chunk Attention with YARN: Enhances performance on long contexts and better achieves length extrapolation.
QKV Bias: Used for attention computation, enhancing model capacity and training stability.

2. MoE Model Architecture

Hybrid Design of Shared and Routing Experts: Enhances the model’s flexibility and task adaptability.
Expert Initialization Method: Enhances the model’s exploration capability and diversity through parameter shuffling and random initialization.
Routing Mechanism: Ensures that only a portion of experts are activated during inference, reducing computational costs.

Dense Model Architecture

Qwen adopts an improved version of the Transformer architecture, similar to GPT, utilizing a decoder-based structure. Most of the technology comes from Meta’s open-source large model LLaMA architecture design, such as RoPE Rotary Positional Encoding, SwiGLU Activation Function, Pre-Normalization, RMSNorm, Grouped Query Attention (GQA), etc.

Overall Architecture

Qwen Technical Architecture Diagram

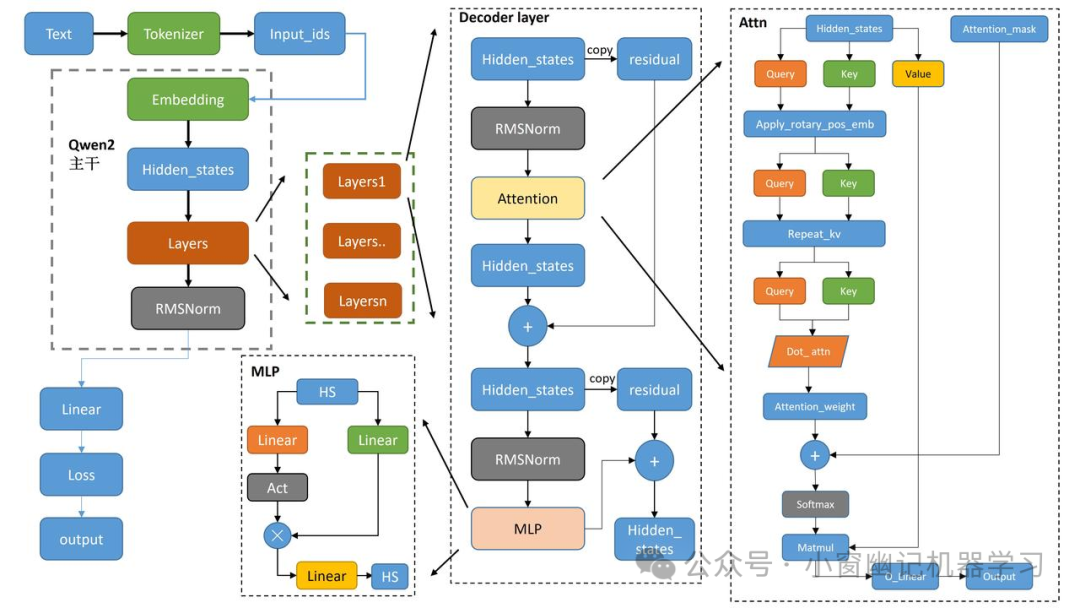
Qwen Series Technical Interpretation 3 - Architecture

Main Part of Qwen2:

Text input is encoded into Input_ids through Tokenizer, then fed into the Embedding layer.
The output of Embedding goes through Hidden_states and is then passed to multiple Layers. Each Layer undergoes normalization via RMSNorm.
The output of Layers enters the Decoder layer on the right.

Decoder Layer:

Hidden_states are normalized through RMSNorm and passed to the Attention module.
Within the Attention module, the input is divided into Query, Key, and Value for attention mechanism computation.
The output after Attention is further processed through another RMSNorm and then through an MLP (Multi-Layer Perceptron).
Each step has a residual connection ensuring the flow of information is not lost.

Attention Mechanism (Right Side):

Hidden_states generate Query, Key, and Value respectively, and apply Rotary positional embedding for positional encoding.
These encoded Query, Key, and Value undergo attention computation to generate Attention_weight.
Attention_weight is normalized via Softmax and multiplied by Value (Matmul), finally outputting O_Linear.

MLP Module:

MLP consists of two linear layers and an activation function, responsible for further feature extraction.

Output Layer:

Finally, the linear layer computes Loss and generates the final Output.

SwiGLU Activation Function

SwiGLU is a variant of the Gated Linear Units (GLU) activation function, proposed by Noam Shazeer in the paper “GLU Variants Improve Transformer.” Below is an introduction to the SwiGLU activation function and related GLU and Swish activation functions.

GLU

x: Input to the neural network
Weight matrices W and V: Two weight matrices for linear transformations
Bias terms b and c: Bias terms for adjusting linear transformations
Sigmoid activation function: Applied to (xW + b) linear transformation

Swish Activation Function:

Is a Sigmoid function
Is a tunable hyperparameter

SwiGLU Formula:

Summary:

Model is more stable
Computational complexity is not high
Both pre-training and fine-tuning effects are good

RMSNorm

Overview: RMSNorm (Root Mean Square Layer Normalization) is a normalization technique used for deep learning models, particularly suitable for architectures like Transformer. It serves as an alternative to LayerNorm, aiming to simplify the normalization process, reduce computational complexity, while maintaining or enhancing model performance.

RMSNorm Scheme

Given an input vector , where is the feature dimension, the computation process of RMSNorm is as follows:

4.1. Compute Root Mean Square (RMS):

4.2. Normalize the input vector:

4.3. Apply scaling and offset parameters:

Where:

: Learnable scaling parameter (same as input dimension).
: Learnable offset parameter (same as input dimension).
: Represents element-wise multiplication operation.

Traditional LayerNorm Scheme

LayerNorm is widely used in Transformer models. It normalizes the feature dimensions of each sample, reducing internal covariate shift. LayerNorm requires computing the mean and variance of input features, which incurs significant computational complexity and overhead.

1.Compute Mean and Variance

2.Normalization Operation

Advantages Summary

Comparisons show that RMSNorm simplifies the normalization process, reduces computational complexity, and provides a more effective normalization method.

Computational Complexity: RMSNorm reduces the computation of mean, decreasing overall computational load.
Numerical Stability: RMSNorm avoids situations where variance approaches zero, enhancing numerical stability.
Performance: In certain tasks, RMSNorm can achieve or exceed the performance of LayerNorm.
Ease of Implementation: Due to its simple computation process, RMSNorm is easy to implement across various deep learning frameworks.

For deep learning models requiring efficient normalization operations, RMSNorm is a choice worth considering.

Grouped Query Attention (GQA)

Qwen2 adopts GQA (Grouped Query Attention), replacing the previous MHA (Multi-Head Attention) in Qwen. GQA optimizes the use of KV cache during inference, significantly improving throughput.

MHA (Multi-Head Attention)

MHA is the most classic attention mechanism in Transformer models, proposed by Vaswani et al. in 2017.

Core Idea:

Each token in the input sequence is mapped to multiple independent query (Query), key (Key), and value (Value) heads.
Each head computes attention scores independently, then concatenates the outputs of all heads, obtaining the final result through linear transformation.

Computation Process:

The input sequence generates h groups of independent Query, Key, and Value through linear transformations.
Each group of Query, Key, and Value computes attention scores:

All heads’ outputs are concatenated and transformed linearly to obtain the final result.

Advantages:

The multi-head mechanism can capture information from different subspaces in the input sequence, enhancing the model’s expressive capability.

Disadvantages:

Computational and memory overhead is significant, especially when the number of heads h is large.

MQA (Multi-Query Attention)

MQA is a simplified version of MHA, designed to reduce computational and memory overhead.

Core Idea:

Uses multiple query heads but shares a single set of keys (Key) and values (Value) heads.
That is, all query heads share the same Key and Value.

Computation Process:

The input sequence generates h groups of independent Query, but only one set of Key and Value.
Each group of Query computes attention scores with the shared Key and Value.
All heads’ outputs are concatenated and transformed linearly to obtain the final result.

Advantages:

Significantly reduces the number of Key and Value, thus lowering computational and memory overhead.
During inference, KV cache has a smaller memory footprint.

Disadvantages:

Since Key and Value are shared, some expressive capability may be lost.

GQA

GQA is positioned between MHA and MQA. For H Qs:

MHA refers to having H K, V.
MQA has one K and V.
GQA means that for a group, there is only one K and V.

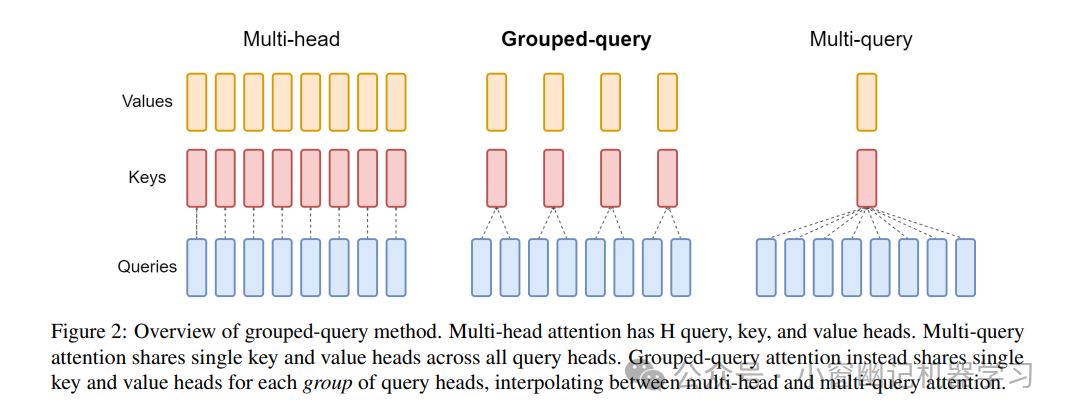
GQA divides the query heads into G groups, each group sharing a single K and V. GQA-G refers to G groups, GQA-1 indicates one group, which is equivalent to MQA, and GQA-H indicates having H K, V, equivalent to MHA.

Advantages of GQA:

GQA is a compromise strategy that is faster than MHA and provides better model quality than MQA.
GQA is not applied to the encoder’s self-attention layer because this part is executed in parallel, where memory is usually not a bottleneck.

Dual Chunk Attention with YARN

Qwen2 implements DCA (Dual Chunk Attention Mechanism), which splits long sequences into manageable length chunks. If the input can be processed within one chunk, DCA will produce the same result as the original attention. DCA helps efficiently capture relative positional information both within and across chunks, thereby improving performance on long contexts. Additionally, YARN is used to readjust attention weights for better length extrapolation.

QKV Bias for Attention Calculation

In Transformer models, QKV Bias refers to the bias terms associated with the linear transformations of query (Query), key (Key), and value (Value). Specifically, QKV bias is an additional parameter used to adjust the results of linear transformations in the self-attention mechanism of Transformers.

QKV Linear Transformation

In the self-attention mechanism of Transformers, the input sequence undergoes three different linear transformations to generate query (Query), key (Key), and value (Value):

Query (Q) :
Key (K) :
Value (V) :

Where:

is the input sequence.
is the weight matrix.
is the bias term (QKV Bias).

Role of QKV Bias

Role of Bias Terms: Bias terms are used to adjust the results of linear transformations, allowing the model to better fit the data distribution.
Flexibility: By introducing bias terms, the model can learn the features of input data more flexibly, rather than solely relying on the linear transformations of weight matrices.

Implementation of QKV Bias

In practical implementations, QKV bias is optional. Some Transformer implementations (like certain versions of BERT or GPT) may omit QKV bias, directly using the results of linear transformations:

No Bias:
With Bias:

Significance of QKV Bias

Model Capacity: Introducing bias terms can increase the model’s capacity, enabling it to learn more complex features.
Training Stability: In some cases, bias terms can help the model converge faster or improve training stability.

Summary:

QKV Bias is the bias term related to the linear transformations of query, key, and value in the self-attention mechanism of Transformers.
Its role is to adjust the results of linear transformations, increasing the model’s flexibility and capacity.
In practical implementations, QKV bias is optional, and whether to use it depends on model design and task requirements.

MoE Architecture

Qwen2 has open-sourced 4 Dense models and 1 MoE model. The Dense models include sizes 0.5B, 1.5B, 7B, and 72B, while the MoE model has a total of 57B parameters and 14B active parameters. The key structural difference between MoE models and Dense models is that the MoE layer contains multiple feedforward networks (FFNs), each serving as an independent expert.

Core Idea

Replace traditional FFN with MoE FFN containing multiple experts (independent FFNs).
Each token is directed to a specific expert for computation based on the probability assigned by the gating network, computed as: , .

Expert Granularity and Routing

The Qwen2 MoE model combines shared experts with specific routing experts:

Shared experts can be utilized across various tasks.
Specific routing experts are flexibly allocated for special scenarios.

There are a total of 72 experts, among which:

8 shared experts are always used.
Among the 64 routing experts, 8 are activated during each model inference.

This design brings greater flexibility and efficiency to the MoE routing mechanism, allowing the model to precisely match the most suitable expert resources when switching between different tasks and scenarios, optimizing operational efficiency and processing effectiveness.

Expert Initialization Method

The expert initialization method for the Qwen2 hybrid expert (MoE) model is simply setting the initial states for the “little helpers” (experts) in the model so they can better complete tasks, specifically divided into three steps:

Determine the number of copies: First, determine how many times to copy the original feedforward neural network (FFN). This depends on the size of the expert’s intermediate layer, the number of experts, and the size of the original FFN’s intermediate layer.
Shuffle parameters to increase diversity: Shuffle the parameters of the copied FFN along the intermediate dimension. This is like mixing a group of similarly capable little helpers, allowing each “helper team” (fine-grained experts) to have its unique capabilities.
Randomly initialize some parameters: Each fine-grained expert has 50% of its parameters randomly reset. This is akin to giving the “little helpers” some new ideas and capabilities, enabling them to explore new solutions more actively during training.

MoE Summary

Computational Efficiency: By activating only a portion of experts, the consumption of computational resources is reduced.
Task Adaptability: The combination of shared and routing experts allows the model to better adapt to different task requirements.
Parameter Utilization: Through expert initialization and routing mechanisms, the model can utilize parameters more efficiently, enhancing overall performance.

Conclusion

The model architecture of Qwen2 has undergone innovations and optimizations in both dense models and MoE models. The dense model adopts an improved Transformer architecture, combining technologies such as RoPE Rotary Positional Encoding, SwiGLU Activation Function, RMSNorm Normalization, Grouped Query Attention (GQA), significantly enhancing the model’s stability and computational efficiency. The MoE model, by introducing multiple experts and a flexible routing mechanism, further strengthens the model’s expressive capability and task adaptability.

Qwen Series Technical Interpretation 3 – Architecture