Principles of Neural Network Algorithms in Deep Learning

Principles of Neural Network Algorithms in Deep Learning

• Graphical Parameter Calculation

• Junior High Mapping

• Neural Network Mapping?

• What is a Neural Network Algorithm?

• Parameter Solving

• References

What is a Neural Network Algorithm?

Junior High Mapping

In junior high school, we learned about mapping with the equation y = f(x).

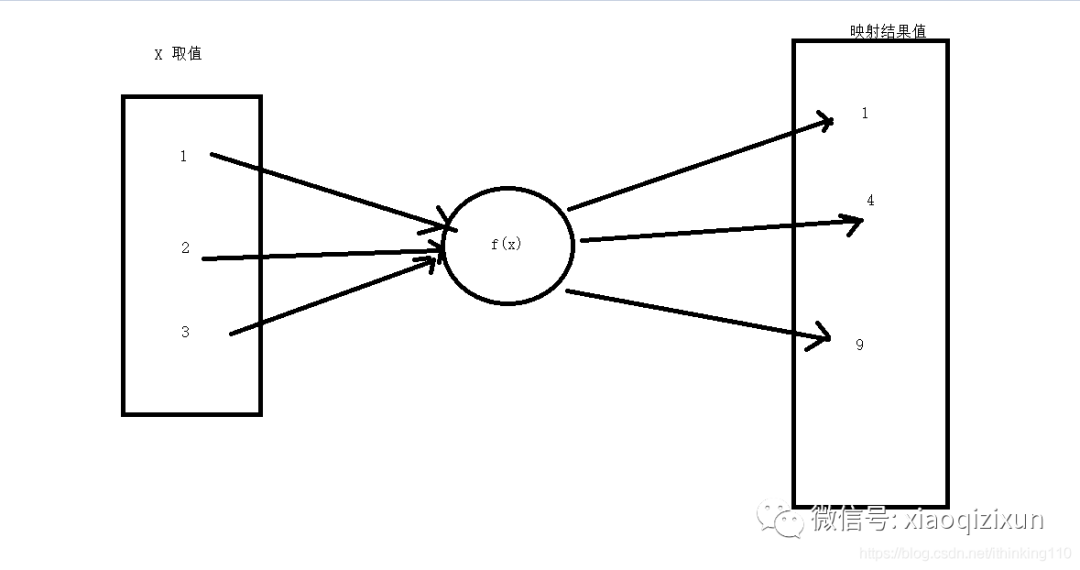
By using several pairs of values x and y, we can derive the formula y = x^2.

Neural Network Mapping?

The following typical neural network also finds the mapping relationship: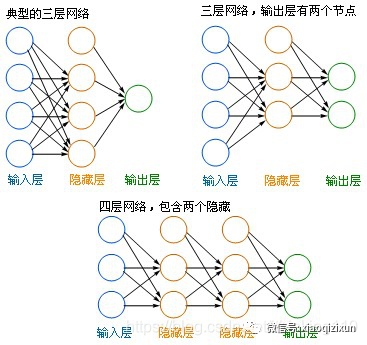1. The blue circle on the left is called the “input layer”; the orange circles in the middle, regardless of how many layers there are, are called “hidden layers”; the green circles on the right are the “output layer”. 2. Each circle represents a neuron, also known as a node. 3. The output layer can have multiple nodes, and multi-node outputs are often used for classification problems. 4. Theoretically, any multilayer network can be approximated using a three-layer network. 5. Generally, the number of nodes in the hidden layer is determined by experience, and the number can be continuously adjusted during testing to achieve optimal results.

It becomes slightly more complex:

From the input layer to the hidden layer: y = f(x)

From the hidden layer to the output layer:

z = f(y)

After going through two classic mappings, it is proven that any complex mapping relationship can be derived using certain mathematical formulas. Therefore, a neural network seeks to map x → y → z.

Parameter Solving

In most cases, we only have the input and output, but how do we solve for the parameters in the function f(x) in between?

Since the birth of artificial neural networks in the 1960s, people have been continuously trying various methods to solve this problem. It wasn’t until the 1980s, with the introduction of the backpropagation algorithm (BP algorithm), that a truly effective solution was provided, reviving research in neural networks.

Forward Propagation: From the input layer to the hidden layer and then to the output layer. The BP (Back Propagation Neural Network) algorithm is an effective method for computing partial derivatives. Its basic principle is: using the output result from forward propagation to calculate the error’s partial derivative, then using this partial derivative to perform a weighted sum with the previous hidden layer, propagating backward layer by layer until reaching the input layer (without calculating the input layer), and finally using the partial derivatives obtained from each node to update the weights.

In simple terms, we first assign a value to the parameters, try to calculate the final result, and if it is too large, we reduce the parameter; if it is too small, we increase it. This process involves continuously correcting these parameters.

For ease of understanding, I will use the term “residual (error term)” to represent the error’s partial derivative.

Output layer → Hidden layer: residual = -(output value – sample value) * derivative of the activation function
Hidden layer → Hidden layer: residual = (weighted sum of the residuals from the right layer’s nodes) * derivative of the activation function.

If you just want a rough idea, you can skip the rest.

Graphical Parameter Calculation

If using Sigmoid (logsig) as the activation function, then: Sigmoid derivative = Sigmoid * (1 – Sigmoid)

In the following diagram, x1 and x2 represent input values, and the sample value represents the output value.

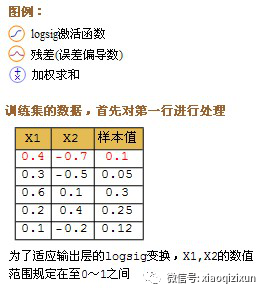
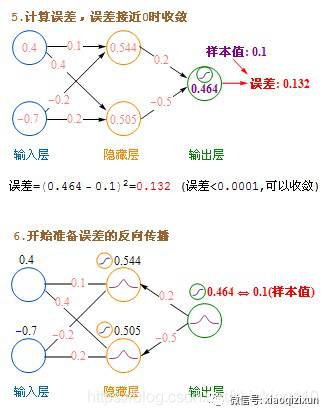
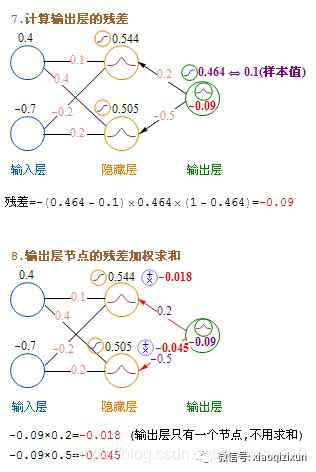
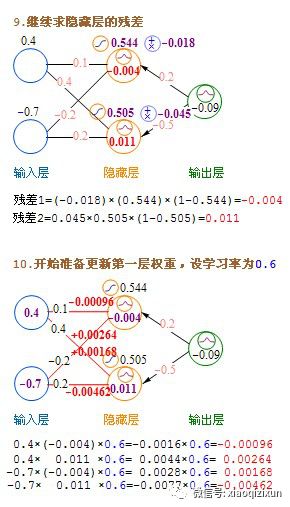
This section introduces the method of updating weights immediately after calculating a record, called stochastic gradient descent. In practice, batch updates yield better results. The method is to calculate each record in the dataset without updating the weights, accumulate the increments to be updated, compute the average, and then use this average to update the weights once, followed by using the updated weights for the next round of calculations. This method is called batch gradient descent.