The “Quick Overview” series of articles aims to disseminate important results from conferences and journals in the field of image graphics, allowing readers to quickly understand relevant academic dynamics in their native language through short articles. We welcome attention and submissions~
◆ ◆ ◆ ◆
Compact 1-Bit Convolutional Neural Networks (BONN) Based on Bayesian Learning
*Corresponding Author: Baocang Zhang ([email protected])
◆ ◆ ◆ ◆
Compared to full-precision counterparts, the performance of 1-bit Convolutional Neural Networks (CNNs) typically declines significantly. In this paper, we propose a 1-bit CNN (BONN) based on Bayesian learning, which can significantly improve the performance of 1-bit CNNs. BONN integrates the prior distributions of full-precision convolution kernels, features, and filters into a Bayesian framework to construct a 1-bit CNN in an end-to-end manner. Our approach can be applied in convolution kernel distribution, feature supervision, and filter pruning, thus optimizing the network simultaneously, greatly enhancing the compactness and performance of 1-bit CNNs. We further introduce a new Bayesian learning-based 1-bit CNN pruning method that significantly improves model efficiency, enabling our method to be used in various practical scenarios. Extensive experiments conducted on the ImageNet, CIFAR, and LFW datasets demonstrate that BONN achieves the best classification performance compared to various state-of-the-art 1-bit CNN models. Additionally, BONN exhibits strong generalization performance in object detection tasks.
Figure 1 Evolution of the Weight Distribution Based on Bayesian Learning
The introduction of Bayesian learning has two advantages:
1. By designing the distribution of weights for each layer, we achieve a more stable bimodal distribution, with fewer weights near the threshold 0 of the sign function, resulting in fewer sign reversals during training.
2. By analyzing the distribution of filters in each layer, we cluster groups with similar distributions during the learning process, minimizing the distance from each filter to the cluster center based on maximum a posteriori probability, thereby obtaining filters with the same distribution for pruning.

Figure 2 Overall Framework of BONN Training
The overall framework of BONN is shown in Figure 2, where we utilize Bayesian learning to train and prune the binary network end-to-end. We investigate the possibility of using Bayesian learning in the pruning of 1-bit CNNs, as Bayesian learning is a mature global optimization scheme. First, Bayesian learning binarizes full-precision convolution kernels into two quantized values (centers) to obtain the 1-bit CNN. Under the premise of minimizing quantization error, when the full-precision convolution kernels follow a mixed Gaussian model, each Gaussian kernel is centered at its corresponding quantized value. Given the two distributions of the 1-bit CNN, we model the full-precision kernels using two Gaussian functions that constitute a mixed model. Subsequently, we designed a pruning framework based on Bayesian learning to prune the 1-bit CNN. Specifically, we divide the filters into two groups, assuming that the filters in one group follow the same Gaussian distribution. We then replace the weights of the filters in that group with their mean values. Figure 2 illustrates the overall framework of BONN, which introduces three innovations during the learning process of the 1-bit CNN: 1) Minimizing the reconstruction error of parameters before and after quantization, 2) Modeling the parameter distribution as a bimodal Gaussian mixture distribution centered at the binarized values (-1, +1), and 3) Pruning the quantized network by maximizing the posterior probability. Based on further analysis, we derived three new losses and corresponding learning algorithms, referred to as Bayesian Kernel Loss, Bayesian Feature Loss, and Bayesian Pruning Loss. These three losses can be used simultaneously. Bayesian learning has inherent advantages in the model quantization and pruning processes. The proposed losses can comprehensively supervise the training process of the 1-bit CNN from both the weight distribution and feature distribution perspectives.
We specifically divide the training process of BONN into two steps: Bayesian Learning-based 1-bit Network Training and Bayesian Learning-based 1-bit Network Pruning.
Given network weight parameters, its quantization code should be as close as possible to its original (full precision) code to minimize quantization error, thus:
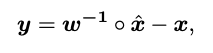
Based on Bayesian learning, under the most likely conditions (corresponding to and , i.e., minimum reconstruction error), we will maximize to optimize the quantization of (e.g., 1-bit CNN), as follows:
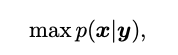
From the perspective of Bayesian learning, we solve this problem through maximum a posteriori (MAP):
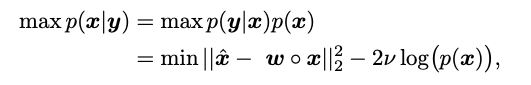
Here:
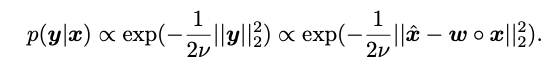
For the 1-bit CNN, is typically quantized into two numbers with the same absolute value. We neglect the overlap between the two numbers, thus, is modeled as a bimodal Gaussian mixture distribution:
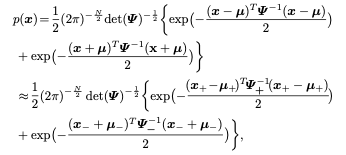
Therefore, the optimization objective can be rewritten as:
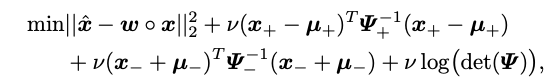
We further designed a Bayesian Feature Loss to alleviate the interference caused by the extreme quantization process in 1-bit CNNs. Considering intra-class compactness, the features of class are assumed to follow a Gaussian distribution, with feature center . We define the Bayesian Feature Loss as follows:
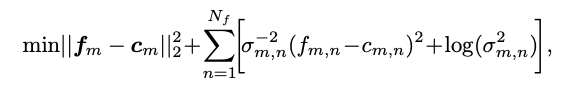
Based on the above analysis, we consider the potential distributions of convolution kernels and features within the same framework and introduce Bayesian loss to enhance the capability of 1-bit CNNs.
