Approximately 3000 words, suggested reading time is 6 minutes.
This article proposes a deep learning framework called DeepLogic, designed to solve problems that involve both logical reasoning and neural perception tasks.1 Introduction
Neuro-symbolic learning aims to combine the perceptual capabilities of deep neural networks (DNNs) with the reasoning capabilities of symbolic reasoning systems. The goal is to integrate neural perception with symbolic logic; however, current research has only linked them sequentially and optimized them separately, failing to fully leverage the mutually enhancing information between them.
This article proposes a deep learning framework called DeepLogic, aimed at solving problems that involve both logical reasoning and neural perception tasks. The contributions of this article are as follows:
-
Proposes the DeepLogic framework with theoretical convergence guarantees, enabling joint learning of neural perception and logical reasoning, allowing them to mutually enhance each other to improve the performance and interpretability of neuro-symbolic reasoning.
-
Introduces a deep logic module (DLM) derived from first-order logic, capable of constructing and learning logical formulas from basic logical operators.
-
Proposes the deep logic optimization (DLO) algorithm, which theoretically quantifies the mutual supervisory signals between neural perception and logical reasoning to ensure their joint learning.
2 DeepLogic Framework
Neuro-symbolic learning research addresses the simultaneous perception and reasoning tasks, where the input is semantic data and the output is unknown complex relationships. To avoid task decomposition, the symbolic attributes of the semantic input to be learned should not be given. The DeepLogic framework mathematically describes the problem formulation and modeling, and proposes a deep & logic optimization (DLO) algorithm for joint learning of neural perception and symbolic reasoning.
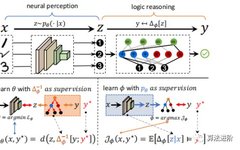
Through our proposed DeepLogic framework, we can jointly learn perception capabilities and logical formulas with a single supervisory signal indicating whether the semantic input satisfies a given formula, as shown in Figure 1. The forward pass (top) processes from semantic input x through intermediate symbolic attributes z to the final deduced label y sequentially. For example, reasoning about the relationships of 1, 2, and 3. First, the system recognizes these images as symbols: ➊, ➋, and ➌ through the neural perception model. Then, the logical reasoning model infers the relationship between ➊, ➋, and ➌, concluding that it satisfies the logical formula: “➊ plus ➋ equals ➌”. In the backward pass (lower left/lower right), the parameters of the perception model θ and the symbolic system φ are iteratively optimized with one another as supervision.
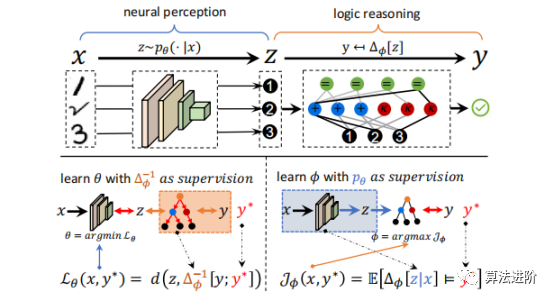Figure 1 DeepLogic Framework
3 Deep Logic Module (DLM)
The deep logic module (DLM) is capable of modeling neural perception and logical reasoning. Specifically, the proposed DLM has the following advantages:
-
DLM does not rely on external knowledge and is easy to implement;
-
DLM adapts to various scenarios by stacking shallow to deep logical layers;
-
DLM can utilize supervisory information to optimize pθ and pφ, ensuring joint learning of neural perception and logical reasoning.
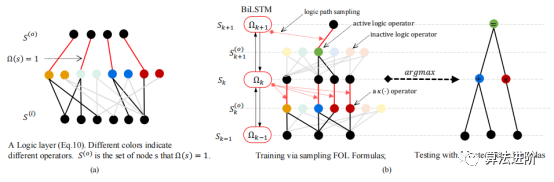Figure 2 (a) A single logical layer as defined in Equation 10; (b) Illustration of the deep logic module (DLM)
In Figure 2 (a), different colors represent different operators, black lines represent the selected symbolic construction S(o), and gray lines represent unselected symbols. During the training phase, active nodes are selected based on Ωk to form a logical tree; during testing, the optimal path is selected to form a new logical tree that best describes the underlying logic, as shown in Figure 2 (b).
4 Deep Logic Optimization (DLO)
The deep logic module (DLM) is a general formula learner based on FOL, capable of learning symbolic relationships between symbols. In this section, we will introduce how DLM and deep neural networks (DNN) handle neuro-symbolic tasks by absorbing semantic inputs and inferring their symbolic relationships. We will also detail the proposed deep logic optimization (DLO) algorithm for jointly optimizing DLM and DNN.
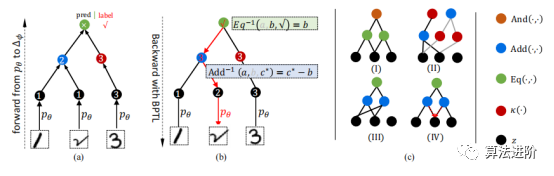Figure 3 (a) Forward propagation of DeepLogic from pθ to Δφ. (b) Backpropagation of DeepLogic using the BPTL algorithm (Algorithm 1). (c) Various cases illustrating Deeplogic formulas: (I) Formula “And(Eq(Z1,Z2),Eq(Z2,Z3))”; (II) Two layers defining the same term “Add(Z1,Z2)” (black line and gray line); (III) and (IV) pathological/self-conflicting cases of formulas; in (III), the equation is always “True”, while in (IV), the BPTL algorithm encounters self-conflict at intermediate nodes.
5 Experiments
In this section, we evaluate the performance, convergence, stability, and generalization ability of the proposed DeepLogic framework on three logical reasoning datasets. The first and second datasets are manually constructed based on MNIST with multiple attributes and different rules, while the third dataset is a widely used reasoning dataset designed to assess machine reasoning capabilities.
5.1 MNIST-ADD
MNIST-ADD is a simple single-digit addition dataset. The task is to learn the “single-digit addition” formula given three MNIST images and a single “True/False” label. This dataset includes 20,000 instances for training and 20,000 instances for testing. We further split the dataset using different partition strategies into α and β splits. In the β split, the test set has additional instances that are different from those in the training set. This setup is also known as “training/testing distribution shift,” which is challenging for neural networks.
The results are summarized in Table 1. On the MNSIT-ADD-α and MNIST-ADD-β datasets, the DNN model overfits the training set. Despite attempts to use methods like changing model size and dropout, the results were poor. The DNN model performed poorly in logical accuracy, especially in handling the imbalanced β split. Compared to the ABL model, our model is more flexible and achieves higher accuracy without the need for Prolog programs. Finally, logical backpropagation aids in providing supervision for the perception model.
Table 1: Accuracy on the MNIST-ADD dataset, where EXTRA SUP indicates whether the model uses additional perception supervision or only a single logical supervision for training, and EXTRA TOOL indicates whether the model uses any additional tools.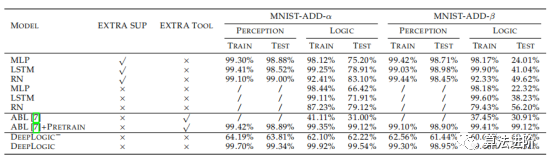
Data Efficiency. As shown in Figure 4 (top), DeepLogic outperforms its DNN counterparts across all settings, converging to over 95% accuracy with just about 100 training images, because neuro-symbolic learning effectively unravels the processes of neural perception and logical reasoning, making it sufficient to train the perception model with a considerable number of images.
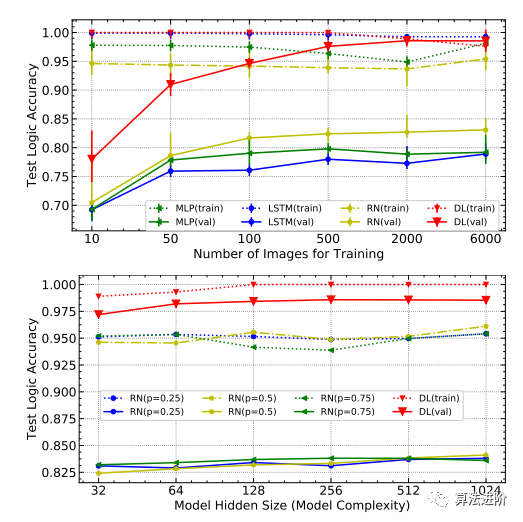Figure 4 Top: Accuracy testing using different scales of training images on MNIST-ADD-α, DL is the abbreviation for DeepLogic; Bottom: Accuracy testing for different model hidden sizes and different dropout probabilities of RN and DL.
Necessity of Pre-training.Pre-training is crucial for system convergence. Experiments show (Figure 5) that DeepLogic converges with just 6 batches of pre-training, and the pre-training cost can be reduced. Higher pre-training accuracy improves the convergence speed of logical learning, especially in multi-rule and multi-attribute scenarios.
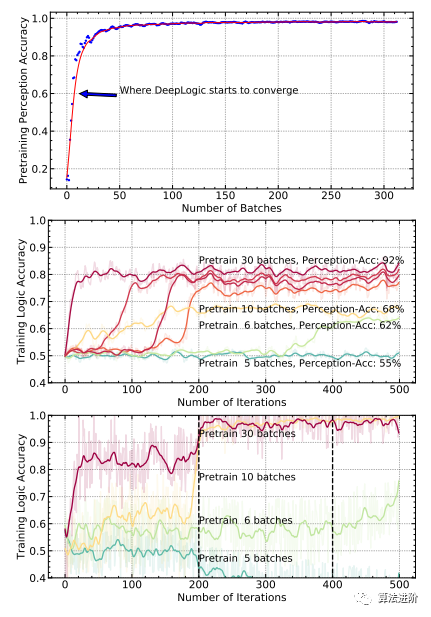Figure 5 Top: PERCEPTION accuracy when pre-training pθ on the MNIST-ADD-α dataset; Middle: LOGIC accuracy of DeepLogic using different batches of pre-training data on the MNIST-ADD-α dataset; Bottom: LOGIC accuracy of DeepLogic using different batches of pre-training data on the MNIST-ADD-α dataset. Key findings are: 1) More pre-training batches ensure better accuracy; 2) DeepLogic ultimately converges with very little pre-training.
Model Stability.This task employs two term layers and one formula layer to learn specific logic, but practical applications may be limited. Experiments indicate (Table 2) that the system learns differently under various settings, with the model converging easily and being robust to different initializations.
Table 2 Typical formulas learned under different settings in the MNIST-ADD dataset. M represents the number of term layers, N represents the number of formula layers. The last column is the percentage of successful convergence in 5 random trials.
5.2 C-MNIST-RULE
C-MNIST-RULE is an extension of MNIST-ADD that includes an additional attribute “color” and two additional formulas “level” and “mutual exclusion”. Note that we use the same DeepLogic model for both MNIST-ADD and C-MNIST-RULE, with the only difference being the number of output formulas Δφ, which is 1 in C-MNIST-RULE and 3 in C-MNIST-RULE. DeepLogic can learn multiple formulas and perceptions simultaneously.
C-MNIST-RULE contains multiple rules and attributes, where we color MNIST images to add color attributes and implement three rules based on Raven’s progressive matrices (RPM). Similar to MNIST-ADD, the C-MNISTRULE dataset contains 20,000 training instances and 20,000 testing instances.
Table 3 shows the accuracy of different models on C-MNIST-RULE. Here, f indicates that the model is trained using additional symbolic annotations, while w indicates no additional symbolic annotations are involved. DeepLogic− does not further train pθ. Both DeepLogic and DeepLogic− undergo 10 batches of pre-training. LOGIC is the accuracy of the final prediction y, while PERCEPTION is the accuracy of predicting hidden symbols z.
Table 3 Accuracy of different models on C-MNIST-RULE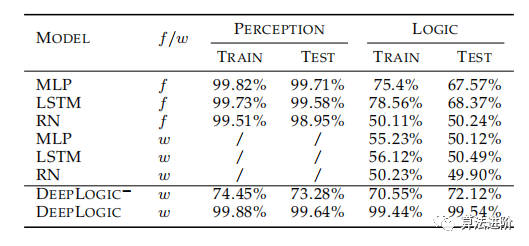
Observations include:
-
Compared to the results without symbolic annotations on CMNIST-RULE, purely DNN-based methods perform poorly.
-
The purely DNN-based method converges with the help of additional symbolic annotations, which is consistent with [15], where pure DNNs, even ResNet, fail to perform better than random guessing without additional annotations.
Figure 6 shows the learning curve of the model on the C-MNIST-RULE dataset.
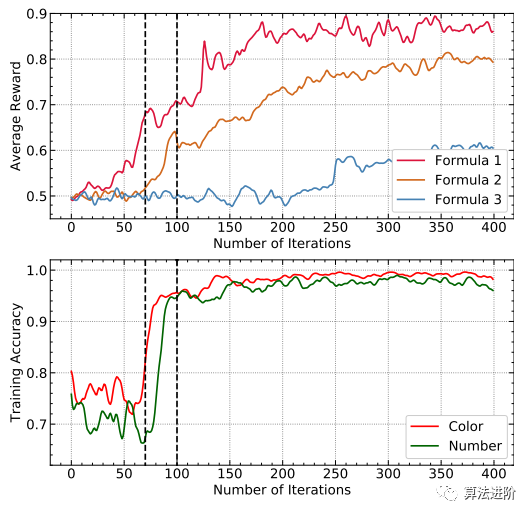Figure 6 Average rewards of three formulas and the accuracy of DeepLogic on two attributes in C-MNIST-RULE
Findings include:
-
Formula 1 converges quickly.
-
The supervision of the Color attribute converges Formula 1.
-
The integrated Color attribute further facilitates the learning of Formula 2 and other formulas.
Figure 7 illustrates several instances from the C-MNIST-RULE dataset, showing logical backpropagation and the final learned formulas.
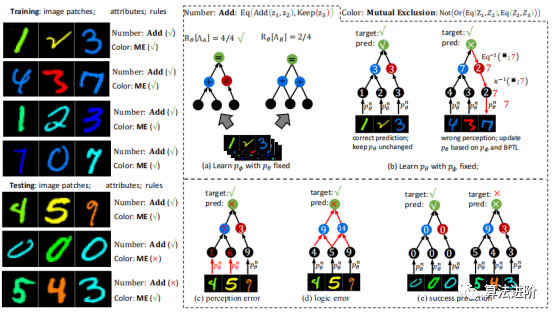Figure 7 Left: Data illustration from the C-MNIST-RULE dataset, where the digit attributes follow the ADD rule, and the color attributes follow the mutual exclusion rule; Right: Training/testing illustrations of digit attributes and Add (rules). (a) and (b) illustrate the process of learning pφ and pθ using Eq.22 and Eq.16, respectively; (c) and (d) are unsuccessful cases due to perception errors (non-optimal pθ) and logical structural errors (non-optimal pφ); (e) Successful cases.
5.3 RAVEN
The RAVEN dataset is developed using Raven’s progressive matrices to measure visual reasoning capabilities. Although fuzzy logic relaxes all logical operations into continuous forms, DLM can be combined with state-of-the-art models like CoPINet to achieve significant performance improvements.
Examples from RAVEN are shown in Figure 8.
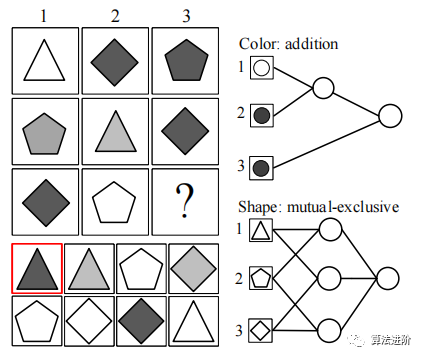Figure 8 DLM module illustration in the RPM task. Images are treated as inputs, then fed into the logic layer, where logical operations are selected from all possible candidate combinations.
The Soft-DLM module, after replacing the original fusion method in CoPINet, shows a significant performance improvement, as shown in Table 4, especially for the “2×2” and “3×3” cases. This validates the generalization capability of DeepLogic and its potential in continuous domains.
Table 4 Testing accuracy on the RAVEN dataset. ACC is the final accuracy, with other columns representing different task configurations.
References:“DeepLogic: Joint Learning of Neural Perception and Logical Reasoning”
Editor: Yu Tengkai
Proofreader: Yang Xuejun
