Click the "Learn Visuals" above, select to add "Star" or "Top"
Heavy content delivered in real-time
There is something that might surprise beginners: Neural network models are not complex! The term ‘neural network’ sounds sophisticated, but in reality, neural network algorithms are simpler than people think.
This article is entirely prepared for beginners. We will understand the principles of neural networks by implementing one from scratch using Python. The outline of this article is as follows:
- Introduction to the basic structure of neural networks – neurons;
- Using the sigmoid activation function in neurons;
- A neural network is just a collection of connected neurons;
- Constructing a dataset where the inputs (or features) are weight and height, and the output (or label) is gender;
- Learning about loss functions and mean squared error loss;
- Training the network to minimize its loss;
- Calculating partial derivatives using backpropagation;
- Training the network with stochastic gradient descent.

Brick: Neuron

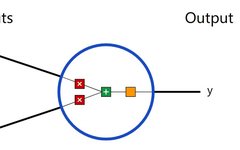
First, let’s take a look at the basic unit of a neural network, the neuron. A neuron receives inputs, performs some operations on the data, and then produces an output. For example, this is a 2-input neuron:
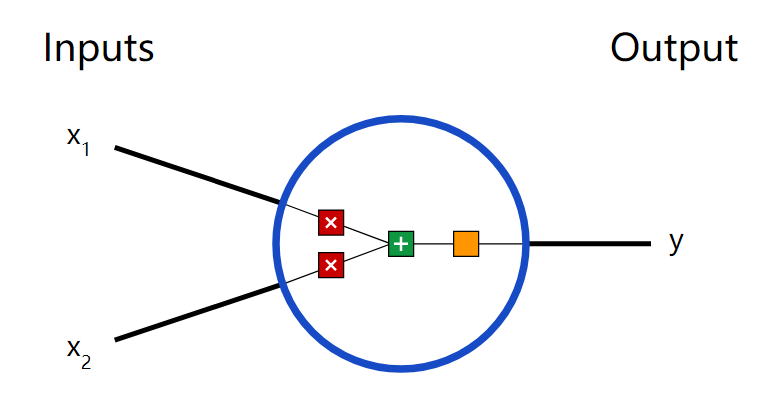
Three things happen here. First, each input is multiplied by a weight (in red):
Then, the weighted inputs are summed and a bias b (in green) is added:
Finally, this result is passed to an activation function f:
The purpose of the activation function is to transform an unbounded input into a predictable form. A commonly used activation function is the sigmoid function:
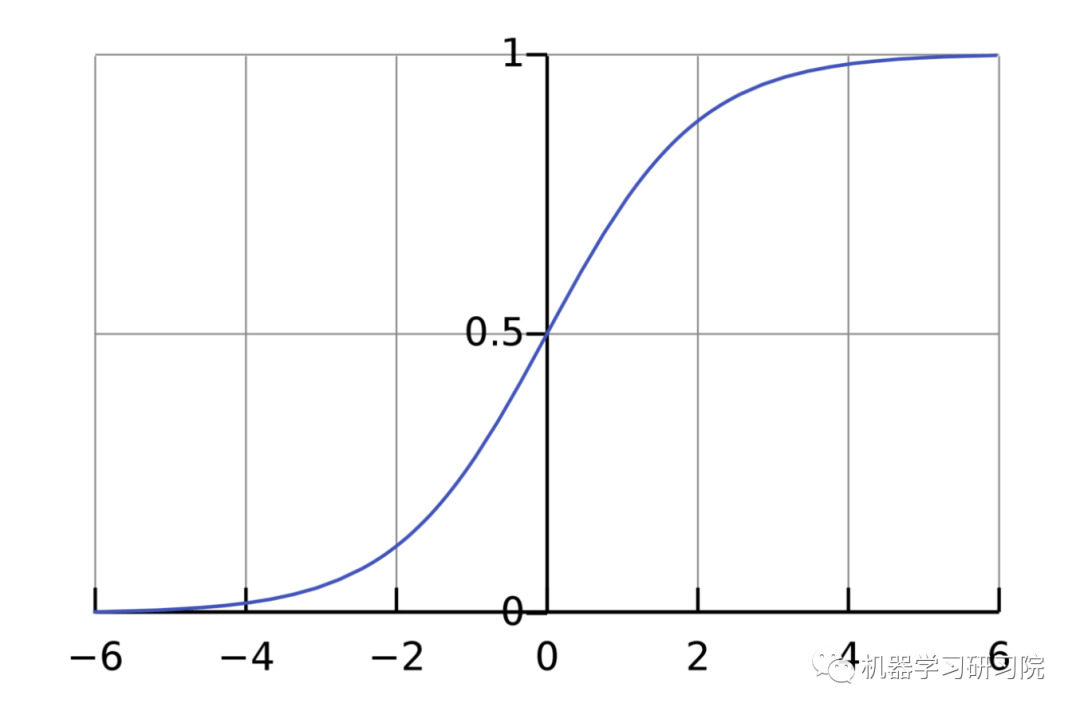
The range of the sigmoid function is (0, 1). Simply put, it compresses (−∞, +∞) to (0, 1), where large negative numbers approximate to 0 and large positive numbers approximate to 1.

A simple example

Suppose we have a neuron with the sigmoid activation function and the parameters as follows:
It is represented in vector form. Now, we give this neuron an input. We use the dot product to represent it:
When the input is [2, 3], the output of this neuron is 0.999. The process of getting an output given an input is called feedforward.

Encoding a neuron

Let’s implement a neuron! Use Python’s NumPy library to complete the mathematical calculations:
import numpy as np
def sigmoid(x):
# Our activation function: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
class Neuron:
def __init__(self, weights, bias):
self.weights = weights
self.bias = bias
def feedforward(self, inputs):
# Weighted input, add bias, then use activation function
total = np.dot(self.weights, inputs) + self.bias
return sigmoid(total)
weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4 # b = 4
n = Neuron(weights, bias)
x = np.array([2, 3]) # x1 = 2, x2 = 3
print(n.feedforward(x)) # 0.9990889488055994
Do you remember this number? It is the 0.999 we calculated earlier in the example.

Assembling neurons into a network

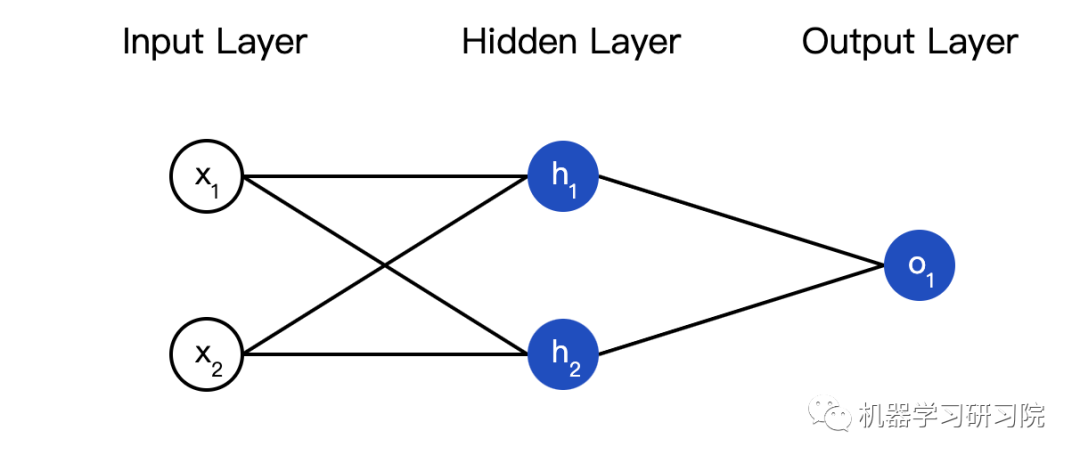
A neural network is a collection of neurons. Here is a simple neural network:
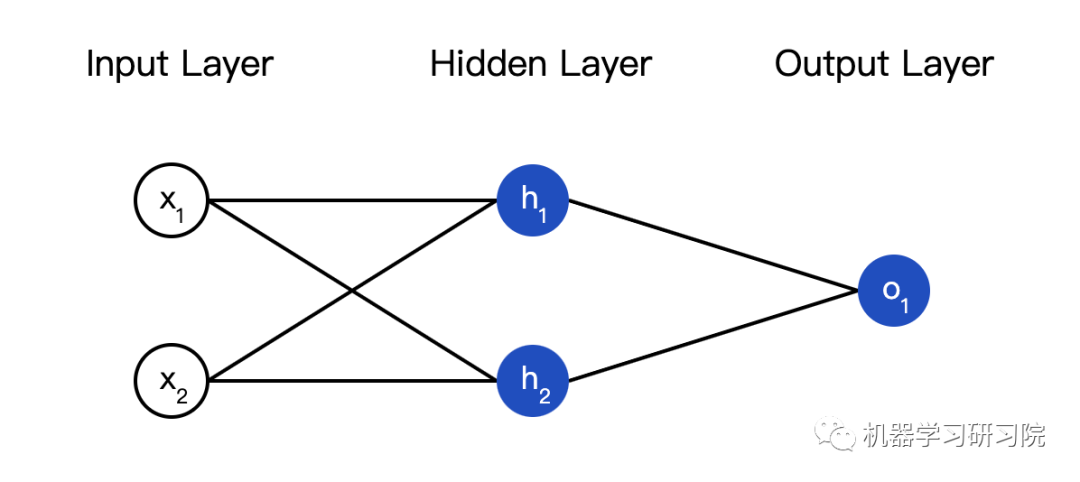
This network has two inputs, a hidden layer with two neurons (h1, h2), and an output layer with one neuron (o1). Note that the input to o1 is the output of h1 and h2, thus forming a network.
The hidden layer is the layer between the input layer and the output layer, and it can have multiple layers.

Example: Feedforward

Continuing with the network from the previous diagram, suppose each neuron’s weights are and the bias is the same with the activation function also being the sigmoid function. Let the corresponding neuron outputs be represented by .
What results do we get when the input is ?
The output of this neural network for the input is 0.7216, which is very simple.
The number of layers in a neural network and the number of neurons in each layer can be arbitrary. The basic logic is the same: inputs are propagated forward through the neural network, ultimately yielding an output. Next, we will continue using this network.

Encoding the neural network: Feedforward

Next, we will implement the feedforward mechanism of this neural network, still using this diagram:
import numpy as np
# ... code from previous section here
class OurNeuralNetwork:
'''
A neural network with:
- 2 inputs
- a hidden layer with 2 neurons (h1, h2)
- an output layer with 1 neuron (o1)
Each neuron has the same weights and bias:
- w = [0, 1]
- b = 0
'''
def __init__(self):
weights = np.array([0, 1])
bias = 0
# This is the neuron class from the previous section
self.h1 = Neuron(weights, bias)
self.h2 = Neuron(weights, bias)
self.o1 = Neuron(weights, bias)
def feedforward(self, x):
out_h1 = self.h1.feedforward(x)
out_h2 = self.h2.feedforward(x)
# The input to o1 is the output of h1 and h2
out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))
return out_o1
network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421
The result is correct, everything seems fine.

Training the neural network: Part 1

Now we have the following data:
| Name | Weight (lbs) | Height (inches) | Gender |
|---|---|---|---|
| Alice | 133 | 65 | F |
| Bob | 160 | 72 | M |
| Charlie | 152 | 70 | M |
| Diana | 120 | 60 | F |
Next, we will use this data to train the weights and biases of the neural network so that we can predict gender based on height and weight:
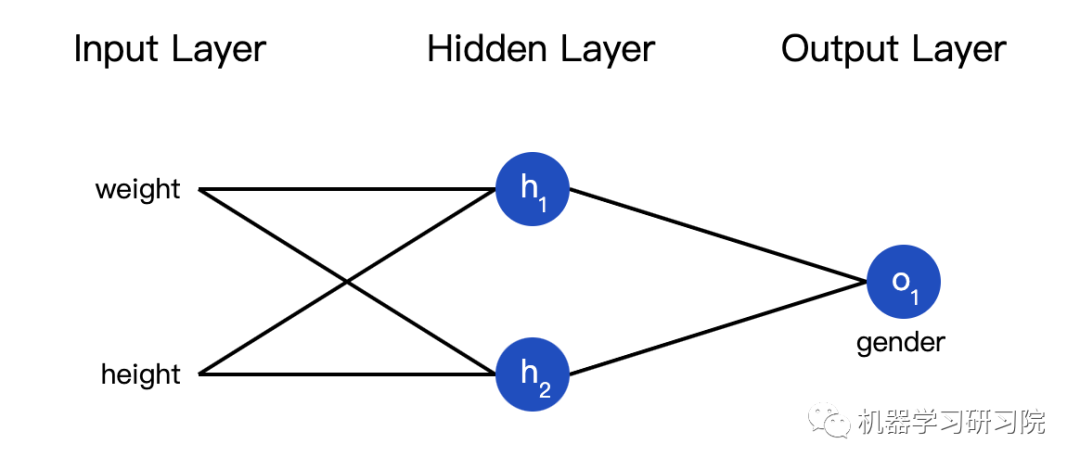
We will represent male (M) as 0 and female (F) as 1, and we have transformed the values:
| Name | Weight (minus 135) | Height (minus 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
I randomly chose 135 and 66 to standardize the data; usually, the mean value is used.

Loss

Before training the network, we need to quantify whether the current network is ‘good’ or ‘bad’, so we can look for a better network. This is the purpose of defining loss.
Here we use mean squared error (MSE) loss: , let’s take a closer look:
- n is the number of samples, which is 4 here (Alice, Bob, Charlie, and Diana).
- y is the variable to predict, which is gender here.
- y_true is the true value of the variable (‘correct answer’). For example, Alice’s y_true is 1 (female).
- y_pred is the predicted value of the variable. This is the output of our network.
e is called the squared error. Our loss function is the average of all squared errors. The better the prediction, the less the loss.
Better prediction = less loss!
Training the network = minimizing its loss.

Example of loss calculation

Suppose our network always outputs 0, in other words, thinks everyone is male. How does the loss look?
| Name | y_true | y_pred | (y_true – y_pred)^2 |
|---|---|---|---|
| Alice | 1 | 0 | 1 |
| Bob | 0 | 0 | 0 |
| Charlie | 0 | 0 | 0 |
| Diana | 1 | 0 | 1 |

Code: MSE loss

Here is the code to calculate the MSE loss:
import numpy as np
def mse_loss(y_true, y_pred):
# y_true and y_pred are numpy arrays of the same length.
return ((y_true - y_pred) ** 2).mean()
y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])
print(mse_loss(y_true, y_pred)) # 0.5
If you do not understand this code, you can take a look at the quick start guide on NumPy regarding array operations.
Alright, let’s continue.

Training the neural network: Part 2

Now we have a clear goal: to minimize the loss of the neural network. By adjusting the weights and biases of the network, we can change its predictions, but how can we gradually reduce the loss?
This section involves multivariable calculus; if you are not familiar with calculus, you may skip the mathematical content.
To simplify the problem, let’s assume our dataset only contains Alice:
Suppose our network always outputs 0, in other words, thinks everyone is male. How does the loss look?
| Name | Weight (minus 135) | Height (minus 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
Then the mean squared error loss is just Alice’s squared error:
We can also see the loss as a function of the weights and biases. Let’s label the weights and biases in the network:
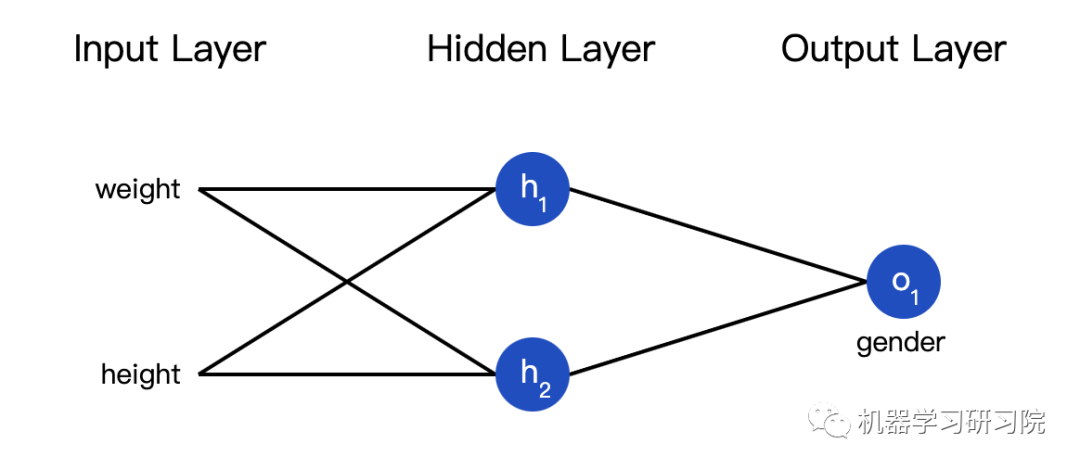
Thus, we can express the network’s loss as:
Suppose we want to optimize w, how will the loss L change when we change w? We can use the partial derivative to answer this question. How to calculate it?
The following data is somewhat complicated; do not worry, prepare paper and pen.
First, let’s rewrite this partial derivative:
Since we already know y, we can calculate
Now let’s tackle y_pred. These are the outputs of the respective neurons, we have:
Since w only affects y_pred (not y), we can do this:
For w, we can also do this:
Here, h is height, and w is weight. This is the second time we have seen the derivative of the sigmoid function. Solving:
We will use this derivative later.
We have already decomposed the loss into several computable parts:
This method of calculating partial derivatives is called the ‘backpropagation algorithm’.
A lot of mathematical symbols; if you haven’t figured it out yet, let’s look at a practical example.

Example: Calculating partial derivatives

We are still looking at the case where the dataset only contains Alice:
| Name | |||
|---|---|---|---|
| Alice | 1 | 0 | 1 |
| Name | Height (minus 135) | Weight (minus 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
Initialize all weights and biases to 1 and 0 respectively. Perform feedforward calculations in the network:
The output of the network is y_pred, which does not have a strong inclination towards Male (0) or Female (1). Let’s calculate
Hint: We have already obtained the derivative of the sigmoid activation function.
Done! This result means that increasing w will slightly increase y_pred.

Training: Stochastic Gradient Descent

Now everything is ready to train the neural network! We will use an optimization algorithm called stochastic gradient descent to optimize the weights and biases of the network to minimize the loss. The core is this update equation:
α is a constant known as the learning rate, used to adjust the speed of training. What we need to do is subtract
- If dL is a positive number, w decreases, L decreases.
- If dL is a negative number, w increases, L increases.
If we optimize each weight and bias in the network this way, the loss will continuously decrease, and the network’s performance will continuously improve.
Our training process is as follows:
- Select a sample from our dataset and optimize using stochastic gradient descent – we optimize for one sample at a time;
- Calculate the partial derivative of each weight or bias (e.g., w1, b1, etc.);
- Update each weight and bias using the update equation;
- Repeat the first step;

Code: A Complete Neural Network

We can finally implement a complete neural network:
| Name | Height (minus 135) | Weight (minus 66) | Gender |
|---|---|---|---|
| Alice | -2 | -1 | 1 |
| Bob | 25 | 6 | 0 |
| Charlie | 17 | 4 | 0 |
| Diana | -15 | -6 | 1 |
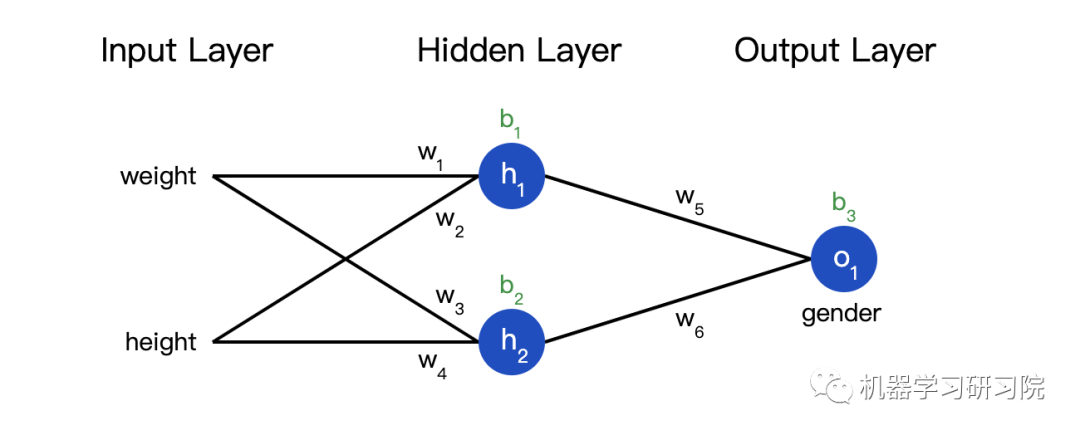
import numpy as np
def sigmoid(x):
# Sigmoid activation function: f(x) = 1 / (1 + e^(-x))
return 1 / (1 + np.exp(-x))
def deriv_sigmoid(x):
# Derivative of sigmoid: f'(x) = f(x) * (1 - f(x))
fx = sigmoid(x)
return fx * (1 - fx)
def mse_loss(y_true, y_pred):
# y_true and y_pred are numpy arrays of the same length.
return ((y_true - y_pred) ** 2).mean()
class OurNeuralNetwork:
'''
A neural network with:
- 2 inputs
- a hidden layer with 2 neurons (h1, h2)
- an output layer with 1 neuron (o1)
*** Disclaimer ***:
The code below is for simplicity and demonstration, not optimal.
Real neural network code is completely different from this. Do not use this code.
Instead, read/run it to understand how this specific network works.
'''
def __init__(self):
# Weights
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# Biases
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def feedforward(self, x):
# X is a numeric array with 2 elements.
h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
return o1
def train(self, data, all_y_trues):
'''
- data is a (n x 2) numpy array, n = # of samples in the dataset.
- all_y_trues is a numpy array with n elements.
Elements in all_y_trues correspond to those in data.
'''
learn_rate = 0.1
epochs = 1000 # Number of times to go through the entire dataset
for epoch in range(epochs):
for x, y_true in zip(data, all_y_trues):
# --- Do a feedforward (we will need these values later)
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = sigmoid(sum_o1)
y_pred = o1
# --- Calculate partial derivatives.
# --- Naming: d_L_d_w1 represents "partial L / partial w1"
d_L_d_ypred = -2 * (y_true - y_pred)
# Neuron o1
d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
d_ypred_d_b3 = deriv_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)
# Neuron h1
d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
d_h1_d_b1 = deriv_sigmoid(sum_h1)
# Neuron h2
d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
d_h2_d_b2 = deriv_sigmoid(sum_h2)
# --- Update weights and biases
# Neuron h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# Neuron h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2
# Neuron o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3
# --- Calculate total loss at the end of each epoch
if epoch % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = mse_loss(all_y_trues, y_preds)
print("Epoch %d loss: %.3f" % (epoch, loss))
# Define dataset
data = np.array([
[-2, -1], # Alice
[25, 6], # Bob
[17, 4], # Charlie
[-15, -6], # Diana
])
all_y_trues = np.array([
1, # Alice
0, # Bob
0, # Charlie
1, # Diana
])
# Train our neural network!
network = OurNeuralNetwork()
network.train(data, all_y_trues)
As the network learns, the loss steadily decreases.
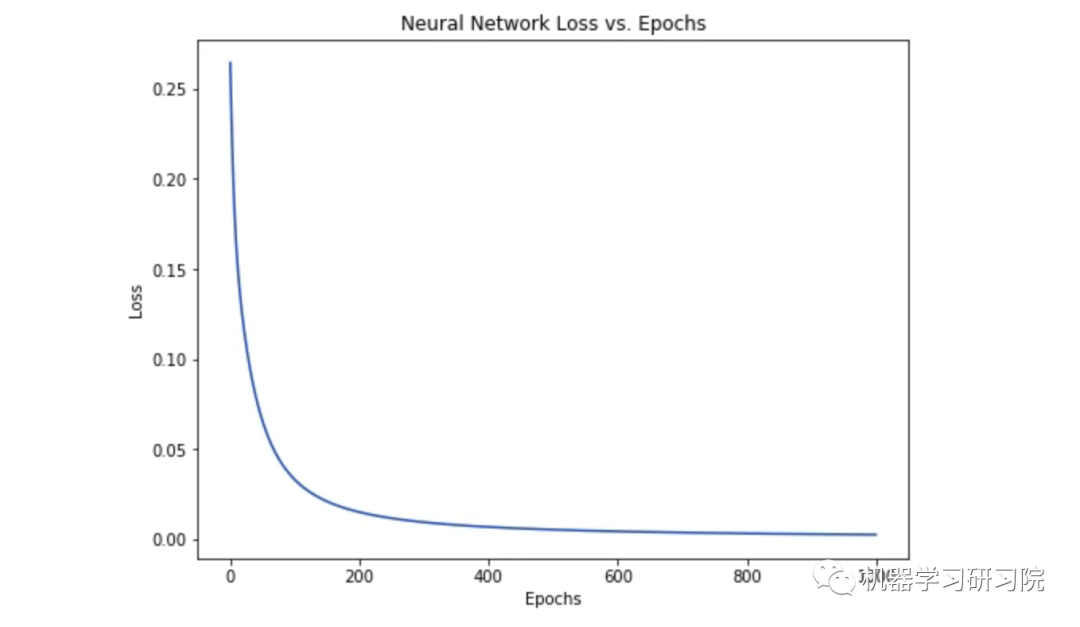
Now we can use this network to predict gender:
# Make some predictions
emily = np.array([-7, -3]) # 128 lbs, 63 inches
frank = np.array([20, 2]) # 155 lbs, 68 inches
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M

What’s next?

We have completed a simple neural network, let’s quickly review:
- Introduced the basic structure of neural networks – neurons;
- Used the sigmoid activation function in neurons;
- Explained that a neural network is a collection of connected neurons;
- Constructed a dataset with inputs (or features) as weight and height, and outputs (or labels) as gender;
- Learned about loss functions and mean squared error loss;
- Trained the network to minimize its loss;
- Calculated partial derivatives using backpropagation;
- Trained the network using stochastic gradient descent;
Next, you can:
- Implement larger and better neural networks using machine learning libraries like TensorFlow, Keras, and PyTorch;
- Explore other types of activation functions;
- Explore other types of optimizers;
- Learn about convolutional neural networks, which revolutionized the field of computer vision;
- Learn about recurrent neural networks, commonly used for natural language processing;
-
Download 1: OpenCV-Contrib Extension Module Chinese Tutorial Reply "OpenCV Extension Module Chinese Tutorial" in the background of "Learn Visuals" public account to download the first Chinese version of the OpenCV extension module tutorial, covering installation, SFM algorithms, stereo vision, object tracking, biological vision, super-resolution processing, and more than twenty chapters of content. Download 2: Python Visual Practical Projects 52 Lectures Reply "Python Visual Practical Projects" in the background of "Learn Visuals" public account to download 31 visual practical projects including image segmentation, mask detection, lane line detection, vehicle counting, eyeliner addition, license plate recognition, character recognition, emotion detection, text content extraction, face recognition, etc., to help quickly learn computer vision. Download 3: OpenCV Practical Projects 20 Lectures Reply "OpenCV Practical Projects 20 Lectures" in the background of "Learn Visuals" public account to download 20 practical projects based on OpenCV to achieve advanced learning in OpenCV. Exchange Group Welcome to join the public account reader group to exchange with peers. Currently, there are WeChat groups for SLAM, 3D vision, sensors, autonomous driving, computational photography, detection, segmentation, recognition, medical imaging, GAN, algorithm competitions, etc. (will gradually be subdivided). Please scan the WeChat number below to join the group, and note: "Nickname + School/Company + Research Direction", for example: "Zhang San + Shanghai Jiao Tong University + Visual SLAM". Please follow the format; otherwise, it will not be approved. Successful additions will be invited into relevant WeChat groups based on research direction. Please do not send advertisements in the group, otherwise, you will be removed from the group. Thank you for your understanding~
Author: Victor ZhouOriginal link: https://victorzhou.com/blog/intro-to-neural-networks/