Neural Network Models
It’s that time of the week again! Today, Xiao Jun is sharing neural network models for everyone to learn together!
Neural networks are complex network systems formed by a large number of simple processing units (called neurons) that are widely interconnected. They reflect many of the basic features of brain function and are highly complex nonlinear dynamic learning systems. Neural networks have large-scale parallelism, distributed storage and processing, self-organization, adaptability, and self-learning capabilities, making them particularly suitable for processing problems that require simultaneous consideration of many factors and conditions, as well as imprecise and fuzzy information processing issues.


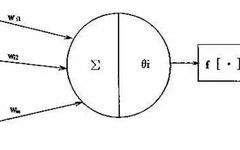
Neurons are information processing units with multiple inputs and a single output, and their processing of information is nonlinear. Based on the characteristics and functions of neurons, they can be abstracted into a simple mathematical model. The artificial neuron model used in engineering is shown in the figure.

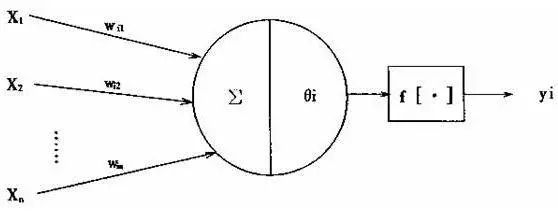
In the figure above, X1, X2, …, Xn are the inputs to the neuron, which are the information A from the axons of the previous n neurons. Σ is the threshold of neuron i; Wi1, Wi2, …, Win are the weight coefficients of neuron i for X1, X2, …, Xn, which represent the transmission efficiency of the synapses; Yi is the output of neuron i; f[·] is the activation function, which determines how neuron i outputs when receiving the combined stimulation of inputs X1, X2, …, Xn and reaching the threshold.

There are various forms of the activation function f[·], with the most common being step, linear, and S-shaped functions, as shown in the figures:


Neural networks have four basic characteristics:
① Nonlinearity
② Non-locality
③ High variability
④ Non-convexity

1、Nonlinearity
Nonlinear relationships are a universal characteristic of nature. The intelligence of the brain is a nonlinear phenomenon. Artificial neurons exist in two different states: activation or inhibition, and this behavior is mathematically represented as a nonlinear relationship. Networks composed of neurons with thresholds perform better, improving fault tolerance and storage capacity.
2、Non-locality
A neural network is typically formed by widely connecting multiple neurons. The overall behavior of a system depends not only on the characteristics of individual neurons but may primarily be determined by the interactions and connections between units. The extensive connections between units simulate the non-locality of the brain. Associative memory is a typical example of non-locality.
3、High variability
Artificial neural networks have adaptive, self-organizing, and self-learning capabilities. Not only can the information processed have various changes, but the nonlinear dynamic system itself also continuously changes while processing information. Iterative processes are often used to describe the evolution of dynamic systems.
4、Non-convexity
The direction of evolution of a system, under certain conditions, will depend on a specific state function. For example, the energy function, whose extrema correspond to the more stable states of the system. Non-convexity means that this function has multiple extrema, leading to multiple relatively stable equilibrium states, which will result in diversity in the evolution of the system.
That’s all for today’s introduction to neural network models. Interested friends can search for more information online to learn; learning is endless, and the fun is infinite! Xiao Jun is always here to make progress with you!