In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Source: PaperWeekly


This article is about 4600 words long, and it is recommended to read it in 10 minutes.
This article analyzes the reversible residual networks as the basis.

Why Use Reversible Networks?

Because both encoding and decoding use the same parameters, the model is lightweight. The reversible denoising network InvDN has only 4.2% of the parameters of the DANet network, yet InvDN performs better in denoising.
Since reversible networks are lossless, they can retain the detailed information of the input data.
No matter how deep the network is, reversible networks use constant memory to compute gradients.

The main purpose is to reduce memory consumption. Currently, all neural networks use backpropagation for training, which requires storing intermediate results of the network to compute gradients, and its memory consumption is proportional to the number of network units. This means that the deeper and wider the network, the greater the memory consumption, which can become a bottleneck for many applications.

Below are the results from the Pytorch summary, where Forward/backward pass size (MB): 218.59 indicates the size of the intermediate variables that need to be saved, which takes up a large portion of the GPU memory (As the network depth increases, the memory occupied by intermediate variables will continue to increase; for resnet152 (size=224), the intermediate variables occupy approximately 606.6÷836.79≈0.725). If we do not store intermediate layer results, we can significantly reduce GPU memory usage, which helps in training deeper and wider networks.

import torch
from torchvision import models
from torchsummary import summary
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
vgg = models.vgg16().to(device)
summary(vgg, (3, 224, 224))

Result:

----------------------------------------------------------------        Layer (type)               Output Shape         Param #================================================================            Conv2d-1         [-1, 64, 224, 224]           1,792              ReLU-2         [-1, 64, 224, 224]               0            Conv2d-3         [-1, 64, 224, 224]          36,928              ReLU-4         [-1, 64, 224, 224]               0         MaxPool2d-5         [-1, 64, 112, 112]               0            Conv2d-6        [-1, 128, 112, 112]          73,856              ReLU-7        [-1, 128, 112, 112]               0            Conv2d-8        [-1, 128, 112, 112]         147,584              ReLU-9        [-1, 128, 112, 112]               0        MaxPool2d-10          [-1, 128, 56, 56]               0           Conv2d-11          [-1, 256, 56, 56]         295,168             ReLU-12          [-1, 256, 56, 56]               0           Conv2d-13          [-1, 256, 56, 56]         590,080             ReLU-14          [-1, 256, 56, 56]               0           Conv2d-15          [-1, 256, 56, 56]         590,080             ReLU-16          [-1, 256, 56, 56]               0        MaxPool2d-17          [-1, 256, 28, 28]               0           Conv2d-18          [-1, 512, 28, 28]       1,180,160             ReLU-19          [-1, 512, 28, 28]               0           Conv2d-20          [-1, 512, 28, 28]       2,359,808             ReLU-21          [-1, 512, 28, 28]               0           Conv2d-22          [-1, 512, 28, 28]       2,359,808             ReLU-23          [-1, 512, 28, 28]               0        MaxPool2d-24          [-1, 512, 14, 14]               0           Conv2d-25          [-1, 512, 14, 14]       2,359,808             ReLU-26          [-1, 512, 14, 14]               0           Conv2d-27          [-1, 512, 14, 14]       2,359,808             ReLU-28          [-1, 512, 14, 14]               0           Conv2d-29          [-1, 512, 14, 14]       2,359,808             ReLU-30          [-1, 512, 14, 14]               0        MaxPool2d-31            [-1, 512, 7, 7]               0           Linear-32                 [-1, 4096]     102,764,544             ReLU-33                 [-1, 4096]               0          Dropout-34                 [-1, 4096]               0           Linear-35                 [-1, 4096]      16,781,312             ReLU-36                 [-1, 4096]               0          Dropout-37                 [-1, 4096]               0           Linear-38                 [-1, 1000]       4,097,000================================================================Total params: 138,357,544Trainable params: 138,357,544Non-trainable params: 0----------------------------------------------------------------Input size (MB): 0.57Forward/backward pass size (MB): 218.59Params size (MB): 527.79Estimated Total Size (MB): 746.96----------------------------------------------------------------

Next, I will first talk about invertible neural networks, then the backpropagation of neural networks, and finally the standard residual networks. For those familiar with the backpropagation algorithm and standard residual networks, you can just look at the first section: Invertible Neural Networks. If you are not familiar with the backpropagation algorithm and standard residual networks, it is recommended to first look at the second section: Backpropagation (BP) Algorithm and the third section: Residual Networks. Sections 1.2 and 1.3.4 are excerpted from @阿亮.

Invertible Neural Networks

Properties of reversible networks:

The size of the input and output of the network must be the same.
The Jacobian determinant of the network is not 0.

1.1 What is the Jacobian Determinant?

The Jacobian determinant, commonly referred to as the Jacobian, is the determinant formed by the partial derivatives of n n-variable functions. In fact, under the premise that the functions are continuously differentiable (i.e., the partial derivatives are continuous), it is the determinant of the coefficient matrix (the Jacobian matrix) in the differential form of the function set. If the dependent variable is continuously differentiable with respect to the independent variable, and the independent variable is continuously differentiable with respect to the new variable, then the dependent variable is also continuously differentiable with respect to the new variable. This can be directly verified using the multiplication rule of determinants and the chain rule of partial derivatives. It is similar to the chain rule of derivatives. The chain rule of partial derivatives also has a similar formula; this is often used in the computation of multiple integrals.

1.2 The Relationship Between Jacobian Determinant and Neural Networks

Why do neural networks relate to the Jacobian determinant? Here, I borrow from Professor Li Hongyi’s PPT (pages 12-14). For those who want to watch the video, you can find it on Bilibili.

Simply put, the relationship between their distributions changes, and because of this, the Jacobian determinant of this network cannot be 0.

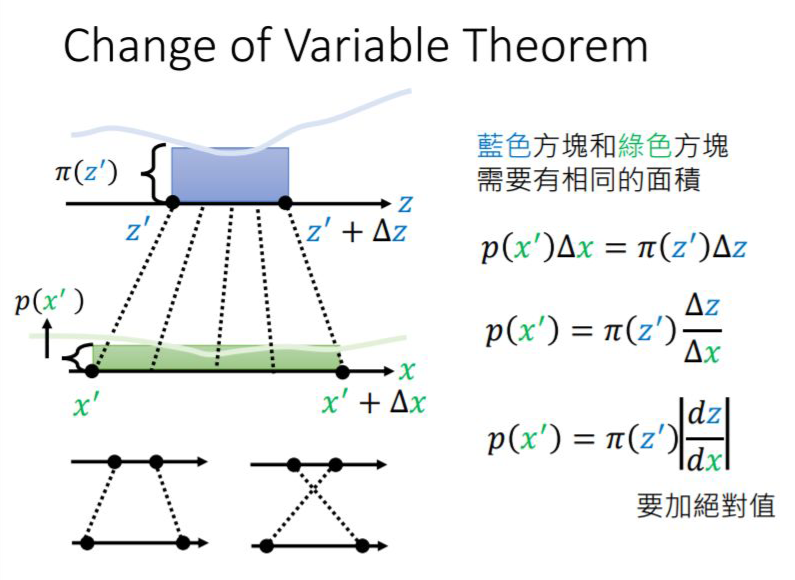
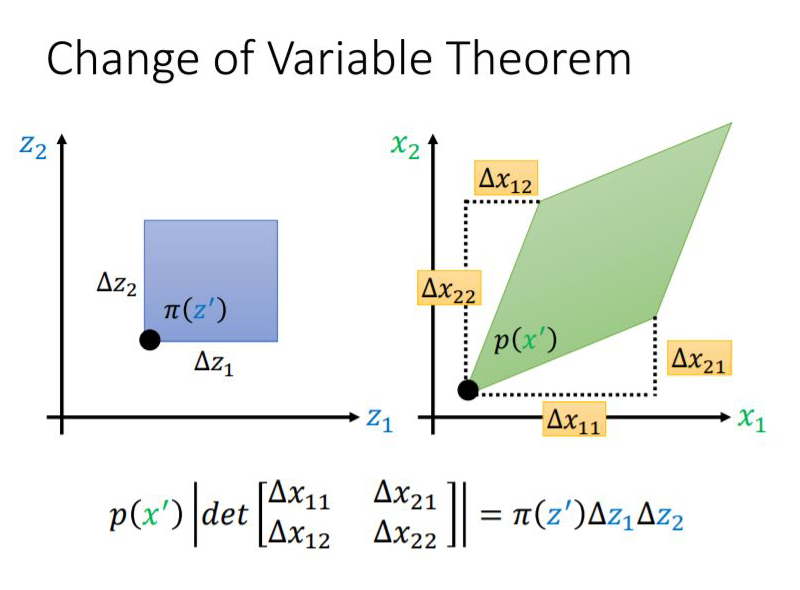
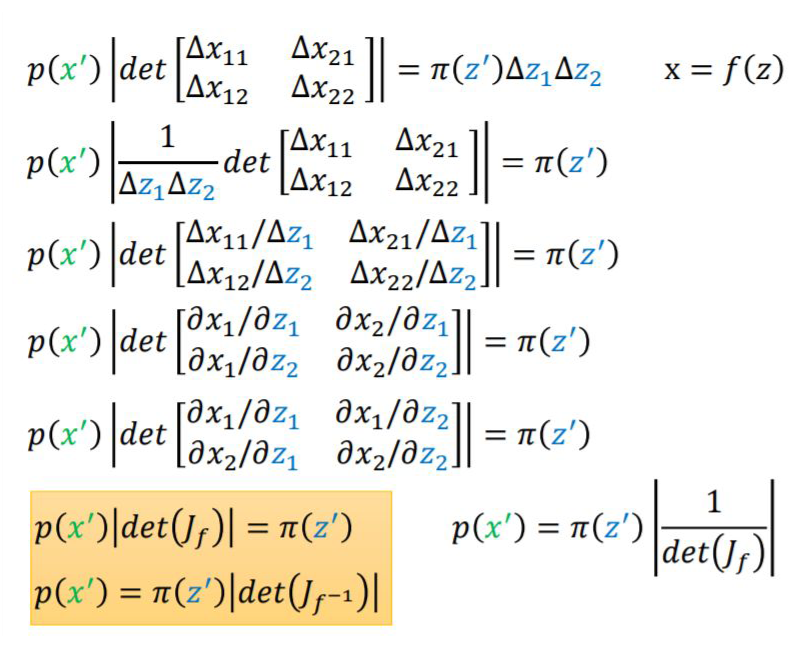
By the way, the loss function optimized for flow-based models is as follows:

Actually, this is very similar to matrix operations; the condition for matrix invertibility is also that the Jacobian determinant of the matrix is not 0, and the Jacobian matrix can be understood as the first derivative of the matrix.

Assuming the expression of the reversible network is:

Its Jacobian matrix is:

Its determinant is 1.

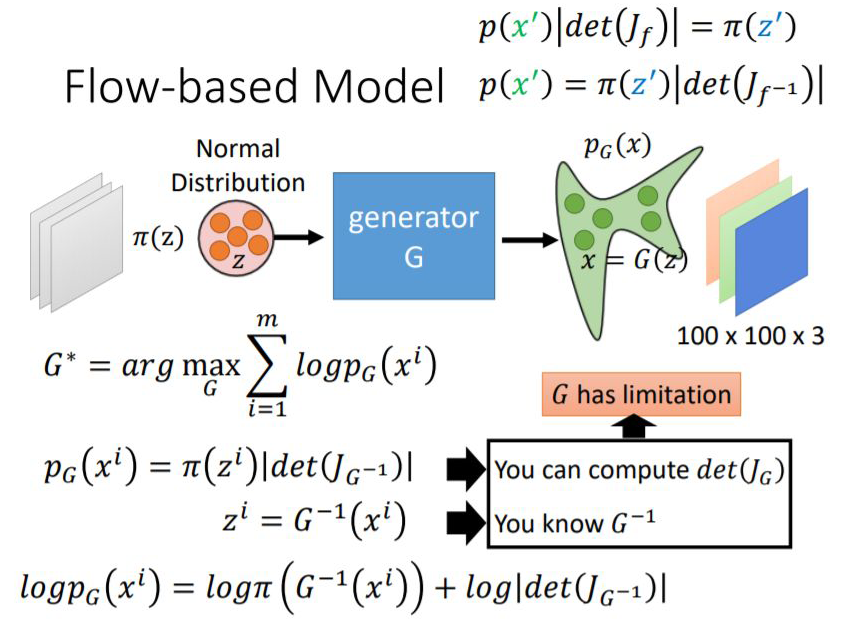
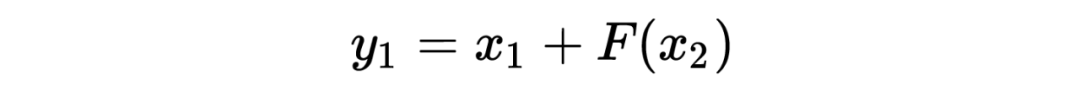
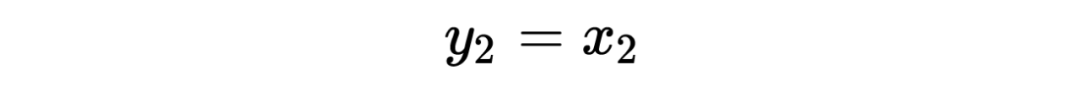
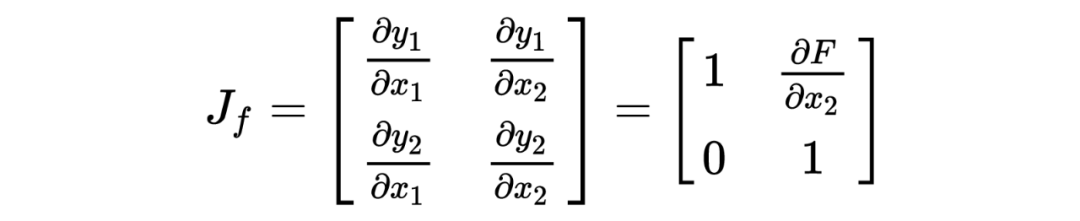
1.3 Reversible Residual Network

Paper Title:

The Reversible Residual Network: Backpropagation Without Storing Activations

Paper Link:

https://arxiv.org/abs/1707.04585

Aidan N. Gomez and Mengye Ren from the University of Toronto proposed the reversible residual neural network, where the activation results of the current layer can be calculated from the results of the next layer. This means that if we know the final result of the network layer, we can backtrack to find the intermediate results of each previous layer. Therefore, we only need to store the parameters of the network and the results of the last layer, making the storage of activation results independent of the depth of the network, which will significantly reduce memory usage. Surprisingly, experimental results show that the performance of the reversible residual network does not significantly decline, and is comparable to previous experimental results of standard residual networks.

1.3.1 Reversible Block Structure

The reversible neural network divides each layer into two parts, namely F and G, where the input of each reversible block is x and the output is y. Its structure is as follows:

Forward Computation Diagram:

Formula Representation:

Reverse Computation Diagram:

Formula Representation:

Where F and G are similar residual functions, referring to the residual network in the above figure. The stride of the reversible block can only be 1, meaning that reversible blocks must be connected one after another, without any other network forms in between; otherwise, information will be lost, and reversible computation will not be possible, which is different from residual blocks. If it is necessary to adopt a structure similar to residual blocks, meaning that a part in the middle uses a normal network form, then the activation results of this middle section must be explicitly stored.

1.3.2 Backpropagation Without Storing Activation Results

To better compute the steps of backpropagation, we modify the formulas for the above forward and reverse computations:

Although x and y have the same values, the two variables represent different nodes in the graph, so their overall derivatives in backpropagation are different. The derivative of x includes the indirect effects produced by y, while the derivative of y is not affected by x.

In the backpropagation computation process, we first provide the activation values of the last layer y and the overall derivative of the error propagation e, then we need to compute its input value x and the corresponding derivative dx, as well as the overall derivative of the weight parameters in the residual functions F and G. The solving steps are as follows:

1.3.3 Computational Overhead

A neural network with N connections has a theoretical multiplication overhead of N for forward computation, and a theoretical multiplication overhead of 2N for backpropagation (backpropagation includes the chain rule of derivatives), while the reversible network requires an additional step to compute the input values in reverse, so the theoretical computational overhead is 4N, which is about 33% more than that of a normal network. However, in practice, the computational overhead for forward and backward operations on the GPU is about the same, and can both be understood as N. In that case, the overall computational overhead for a normal network is 2N, while that for a reversible network is 3N, which is about 50% more.

1.3.4 Calculation of the Jacobian Determinant

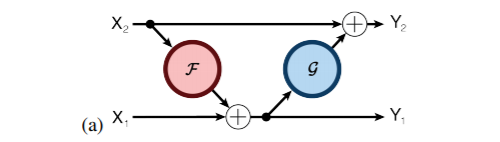
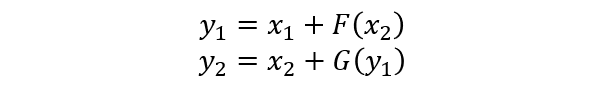
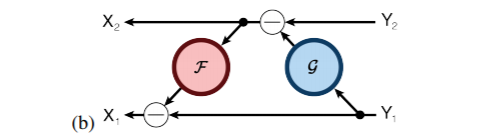
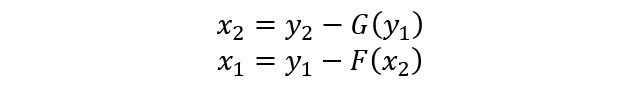
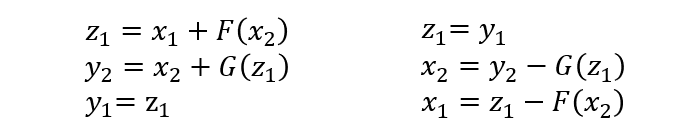
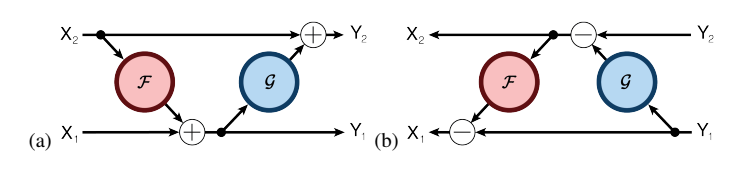
The encoding formula is as follows:

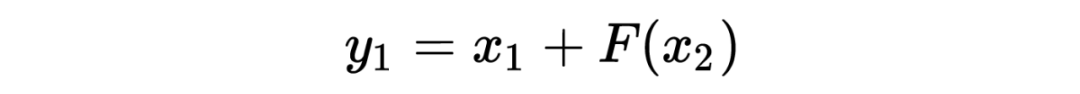
The decoding formula is as follows:

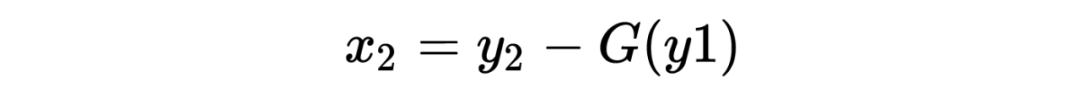
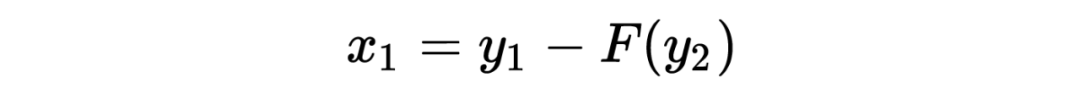
To compute the Jacobian matrix, we can write the encoding formula more intuitively as follows:

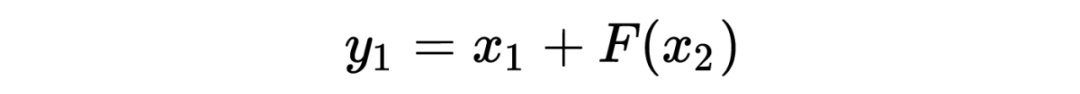
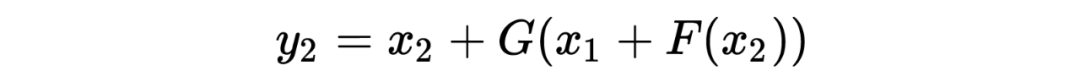
Its Jacobian matrix is:

This Jacobian determinant is also 1, because here dx and dy have the same coefficients.

Another explanation is to cut this dual form in half:

Its determinant is 1.

Because of the dual form, the determinant here is also 1.

Because dx is non-zero, its determinant is also 1.

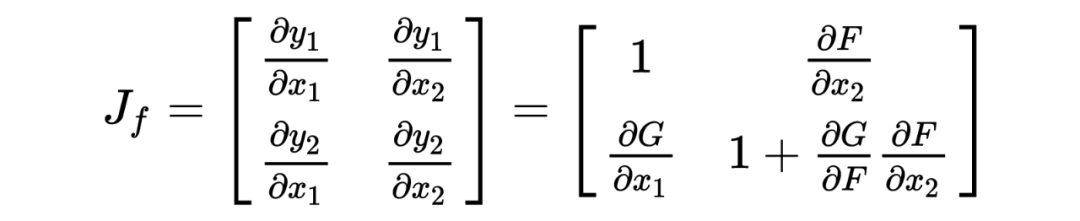
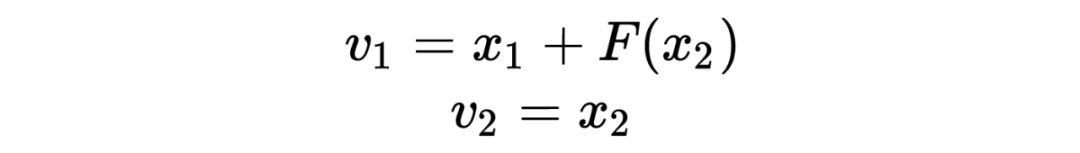
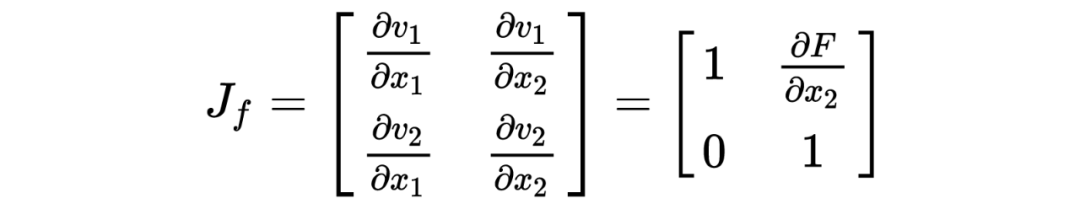
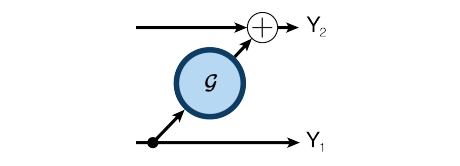
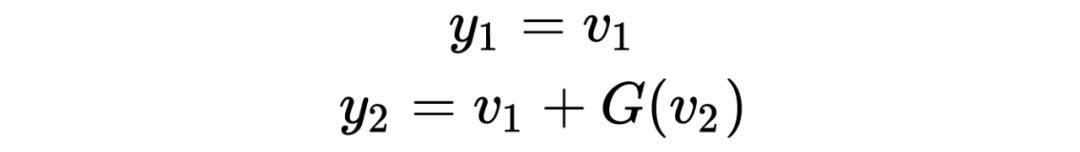
Backpropagation (BP) Algorithm

Meaning of Symbols in the Above Diagram:

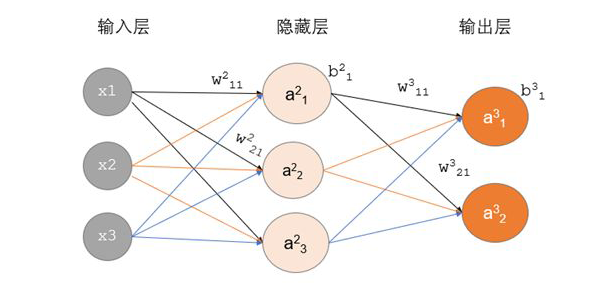
x1, x2, x3: Represents 3 input layer nodes.
w: Represents the weight parameters from layer t-1 to layer t, j represents the j-th node in layer t, and i represents the i-th node in layer t-1.
y: Represents the output result after activation of the i-th node in layer t.
g(x): Represents the activation function.

Forward Propagation Calculation Process:

Hidden Layer (the second layer of the network)

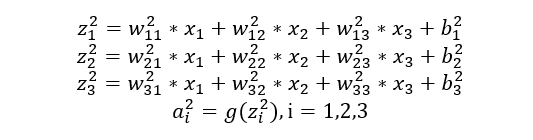
In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Output Layer (the last layer of the network)

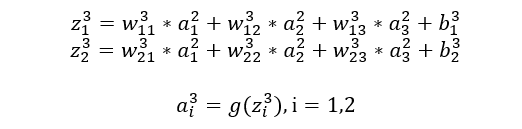
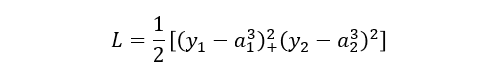
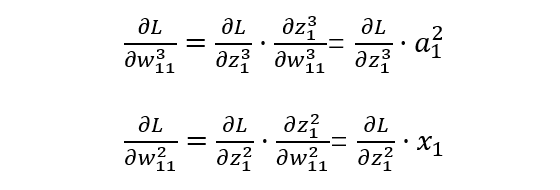
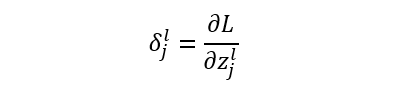
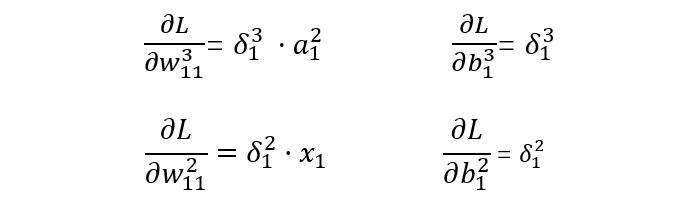
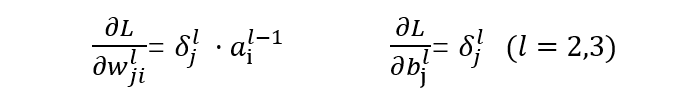
In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Backpropagation Calculation Process:

Taking a single sample as an example, suppose the input vector is [x1,x2,x3], the target output value is [y1,y2], and the cost function is denoted as L. The overall principle of backpropagation is to propagate the overall output error back through the network, calculating the gradients of each layer’s nodes, and updating the weights w and biases b of each layer using the principle of gradient descent, which is also the process of network learning. The advantage of backpropagation is that it can represent complex derivative calculations in a recursive form, simplifying the computation process.

Using squared error to calculate the backpropagation process, the cost function is represented as follows:

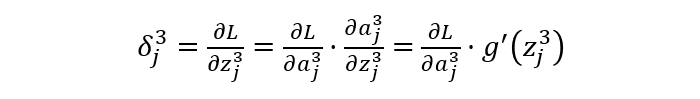
In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

According to the chain rule of derivatives, the weights from hidden to output layer and from input layer to hidden layer are represented as:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Introducing a new representation of the error derivative, called the neural unit error:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

l=2,3 indicates the layer number, and j indicates the j-th node of a certain layer. After replacing the representation, it is as follows:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Thus, we can summarize a general computation formula:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

From the above formula, it can be seen that if the neural unit error δ can be calculated, then the partial derivatives of the total error with respect to the weights w and biases b of each layer can be calculated, and then gradient descent can be used to optimize the parameters.

Solving for the δ of each layer:

Output Layer

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Hidden Layer

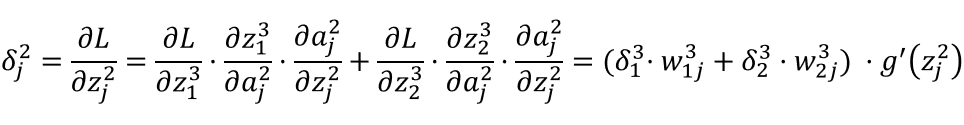
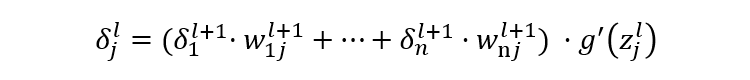
In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

In other words, we can directly calculate the neural error unit δ of the hidden layer based on the neural error unit of the output layer, thus simplifying the complex derivative process of the hidden layer, and we can derive a more general computation process:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

This establishes the relationship between the neural unit error of layer l and that of layer l+1. This is the error backpropagation algorithm; as long as the neural unit error of the output layer is determined, the neural unit errors of other layers do not need to compute derivatives, but can be derived directly through the above formula.

Residual Networks

Residual networks mainly solve two problems (the structure is shown in the figure below):

Gradient vanishing problem;
Network degradation problem.

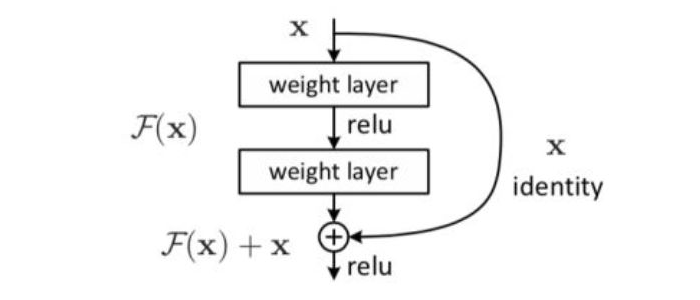
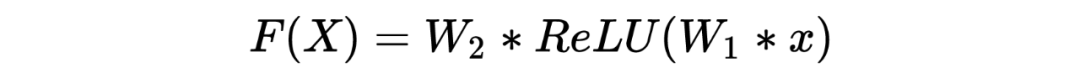
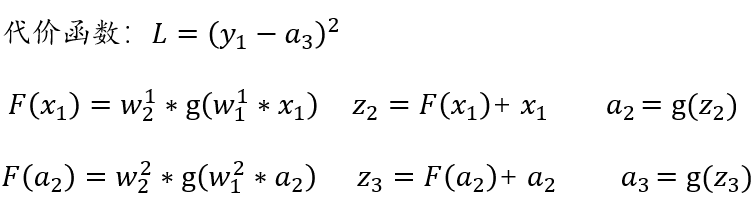
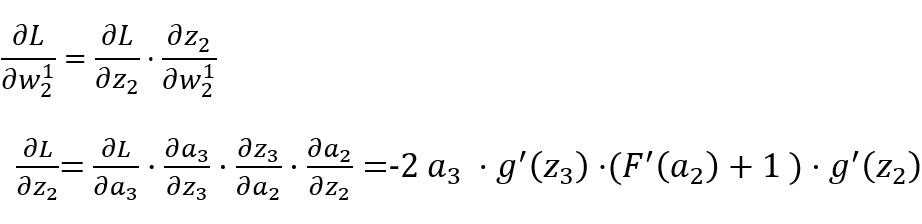
In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

The above structure is a residual block composed of two-layer networks; the residual block can consist of 2, 3, or even more layers. However, if it is a single layer, it becomes a linear transformation, which is meaningless. The above figure can be expressed as follows:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Therefore, before entering the activation function ReLU in the second layer, F(x)+x forms a new input, also called the identity mapping.

The identity mapping means that when the input of this residual block is x, the output is still x, and its goal is to learn F(X)=0.

Here’s a question: why do we add an extra x instead of letting the model directly learn F(x)=x?

Because it is easier to let F(x)=0; initializing the parameters W very small and close to 0 can make the output close to 0. Also, if the output is negative, after the first layer ReLU, the output is still 0; this can make F(x)=0 in many situations. However, letting F(x)=x is indeed very difficult because the parameters must be just right for the final output to be x.

What is the role of identity mapping?

The identity mapping can solve the network degradation problem; as the number of layers in the network increases, the accuracy of the network decreases, meaning that the network itself has an optimal layer structure; both too deep and too shallow can cause model accuracy to decline. With the existence of identity mapping, the network can learn which layers are redundant and can pass through these layers without loss, theoretically allowing deeper networks to not affect their accuracy and solving the network degradation problem.

How can it solve the gradient vanishing problem?

To analyze with an example structure of two residual blocks, where each residual block consists of two layers of neural networks:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Assuming the activation function ReLU is represented by g(x), the sample instance is [x1,y1], meaning the input is x1 and the target value is y1, and the loss function still uses the squared loss function, the calculation of each layer is as follows:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

Next, we derive the weight parameters of the first residual block, according to the chain rule of derivatives, the formula is as follows:

In-Depth Analysis of Invertible Neural Networks: Making Neural Networks Lighter

We can see that the derivative formula has an additional +1 term, which turns the original chain rule product into a sum, effectively avoiding gradient vanishing.

References:

[1] PPT https://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2019/Lecture/FLOW%20(v7).pdf

[2] Reversible Forms of Neural Networks https://zhuanlan.zhihu.com/p/268242678

[3] Significantly Reduce GPU Memory Usage: Reversible Residual Networks (The Reversible Residual Network) https://www.cnblogs.com/gczr/p/12181354.html

[4] Jacobian Determinant https://baike.baidu.com/item/雅可比行列式/4709261?fr=aladdin

[5] The Reversible Residual Network: Backpropagation Without Storing Activations

[6] pytorch-summary https://github.com/sksq96/pytorch-summary

Editor: Huang Jiyan
Proofreader: Lin Yilin

1.1 What is the Jacobian Determinant?

1.2 The Relationship Between Jacobian Determinant and Neural Networks

1.3 Reversible Residual Network

Paper Title:

The Reversible Residual Network: Backpropagation Without Storing Activations

Paper Link:

https://arxiv.org/abs/1707.04585

Backpropagation (BP) Algorithm

Residual Networks

Leave a Comment Cancel reply