Mathematical Principles of Graph Neural Networks

Graph Deep Learning (GDL) has been accelerating its development over the years. Many real-life problems have made GDL a universal tool, showing great potential in areas such as social media, drug discovery, chip implantation, prediction, and bioinformatics.

This article will provide a detailed review and explanation of popular Graph Neural Networks (GNN) and their mathematical subtleties. The idea behind Graph Deep Learning is to learn the structural and spatial features of graphs with nodes and edges, where these nodes and edges represent entities and their interactions.

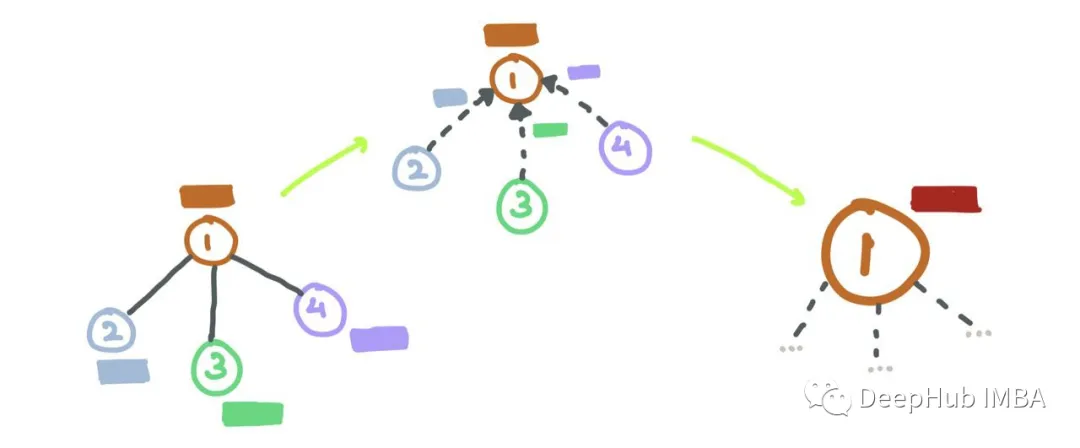
Graphs

Before we delve into Graph Neural Networks, let’s first explore what a graph is in computer science.

A graph G(V,E) is a data structure that consists of a set of vertices (nodes) i ∈ V and a set of edges eij ∈ E that connect vertices i and j. If there is an edge connecting the two nodes i and j, then eij = 1; otherwise, eij = 0. This connection information can be stored in an adjacency matrix A:

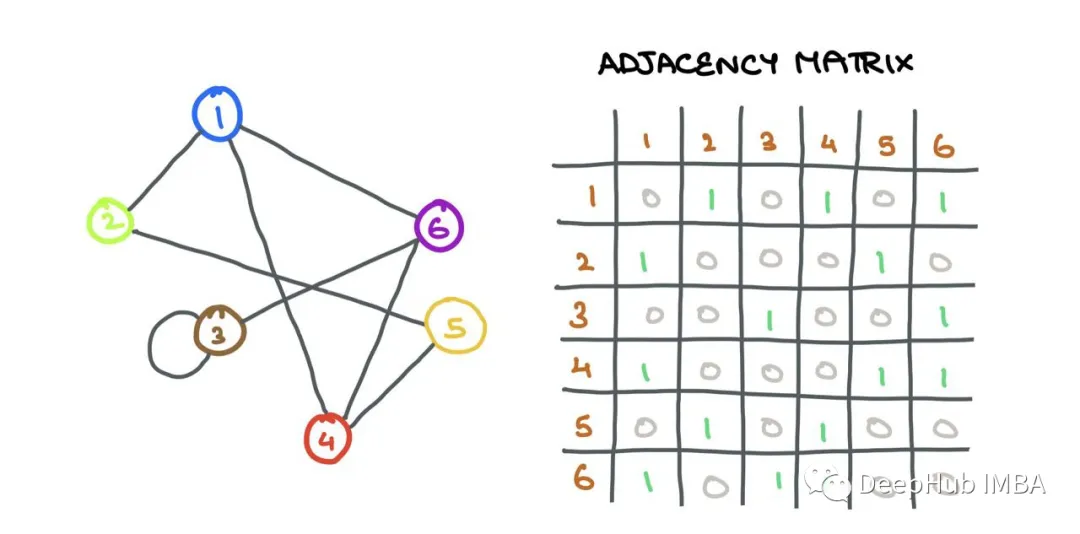
I assume that the graphs in this article are unweighted (without edge weights or distances) and undirected (no directional association between nodes), and that these graphs are homogeneous (single type of nodes and edges; the opposite is “heterogeneous”).

The difference between graphs and regular data is that they have a structure that neural networks must respect; failing to utilize it would be a waste. The following graph is an example of a social media graph, where nodes are users and edges represent their interactions (e.g., following/liking/sharing).

For images, the image itself is a graph! This is a special variant called a “grid graph,” where for all internal nodes and corner nodes, the number of outward edges from a node is constant. There are consistent structures present in image grid graphs that allow for simple convolution-like operations to be performed on them.

Images can be thought of as a special type of graph, where each pixel is a node and is connected to surrounding pixels by dashed lines. Of course, viewing images this way is impractical because it means needing a very large graph. For example, a simple CIFAR-10 image of size 32×32×3 would have 3072 nodes and 1984 edges. For a larger ImageNet image of size 224×224×3, these numbers would be even larger.

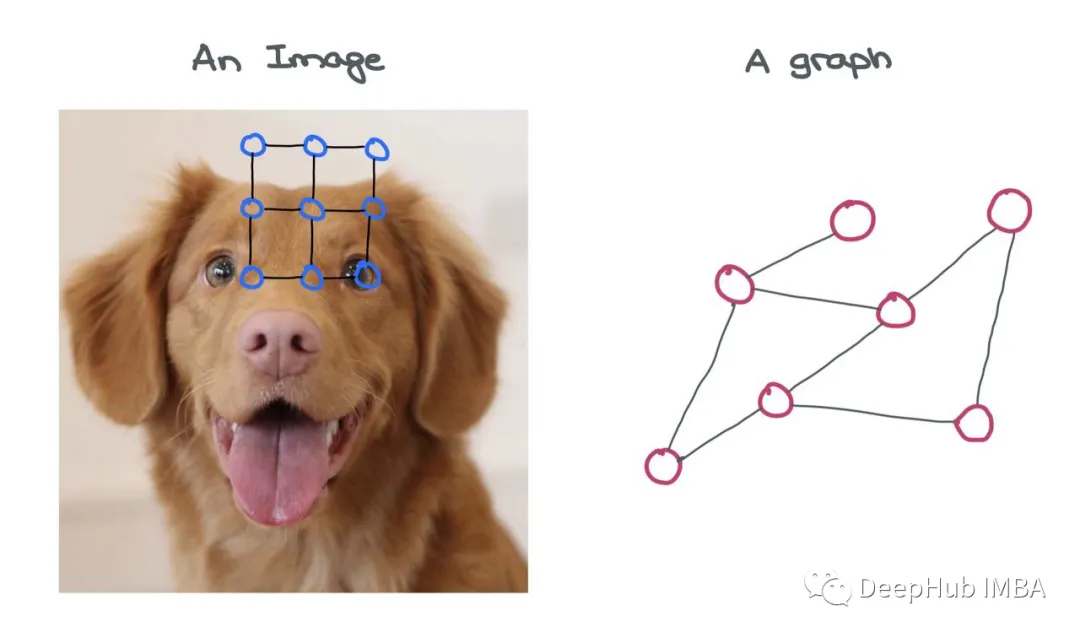
Unlike images, the number of connections between different nodes in a graph varies, and there is no fixed structure; however, it is this structure that adds value to the graph.

Graph Neural Networks

A single Graph Neural Network (GNN) layer consists of a series of steps performed at each node in the graph:

• Message Passing

• Aggregation

• Update

These form the building blocks for learning on graphs, and innovations in GDL occur through changes in these three steps.

Nodes

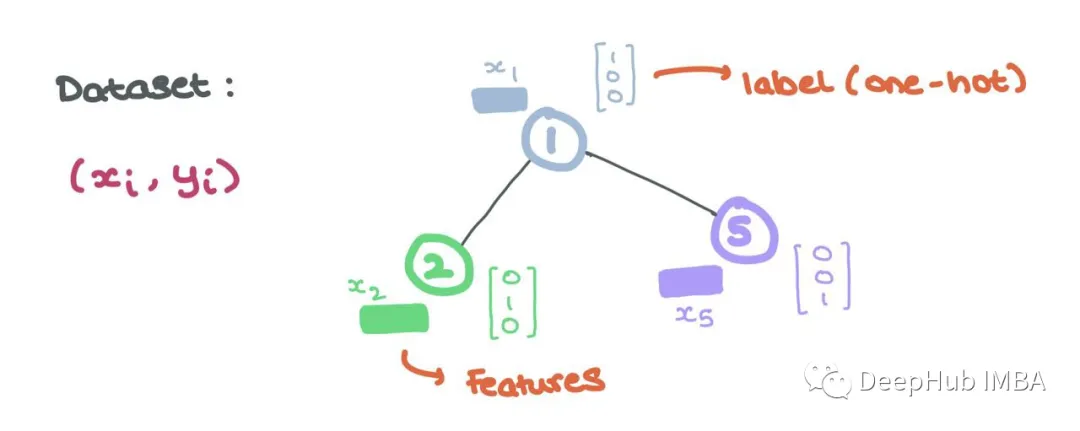
Nodes represent an entity or object, such as a user or an atom. Therefore, nodes have a set of attributes representing the entity they depict. These node attributes form the features of the node (i.e., “node features” or “node embeddings”).

Typically, these features can be represented as vectors in Rd. This vector can either be a latent dimensional embedding or constructed in such a way that each entry is a different attribute of the entity.

For example, in a social media graph, user nodes may have attributes such as age, gender, political inclination, relationship status, etc., which can be represented numerically. In a molecular graph, atom nodes may have chemical properties like affinity for water, force, energy, etc., which can also be represented numerically.

These node features are the input to the GNN, where each node i has associated node features xi ∈ Rd and label yi (which can be continuous or discrete, like one-hot encoding).

Edges

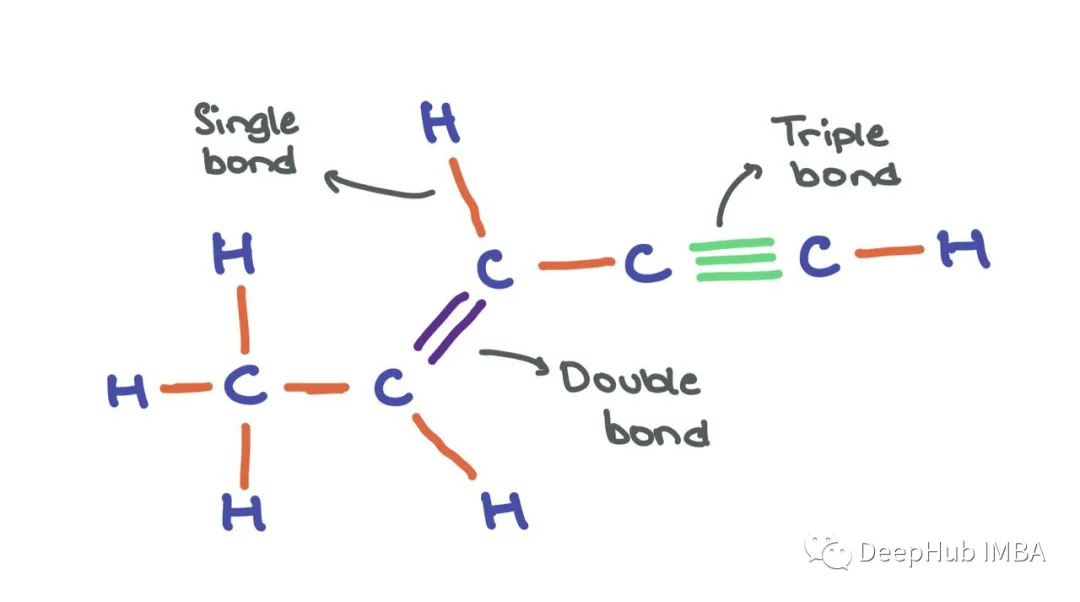
Edges can also have features aij ∈ Rd; for example, in cases where edges are meaningful (like chemical bonds between atoms). We can imagine the following molecule as a graph, where atoms are nodes and bonds are edges. While atom nodes themselves have their own feature vectors, edges can have different edge features that encode different types of bonds (single bond, double bond, triple bond). However, for simplicity, I will omit edge features in this article.

Now that we know how to represent nodes and edges in a graph, let’s start with a simple graph that has a set of nodes (with node features) and edges.

Message Passing

GNN is known for its ability to learn structural information. Typically, nodes with similar features or attributes are connected (for example, in social media). GNN learns how and why specific nodes are connected by examining the neighborhood of nodes.

The neighborhood Ni, which is the set of neighbors of node i, is defined as the set of nodes j that are connected to i by edges. Formally, Ni = {j: eij ∈ E}.

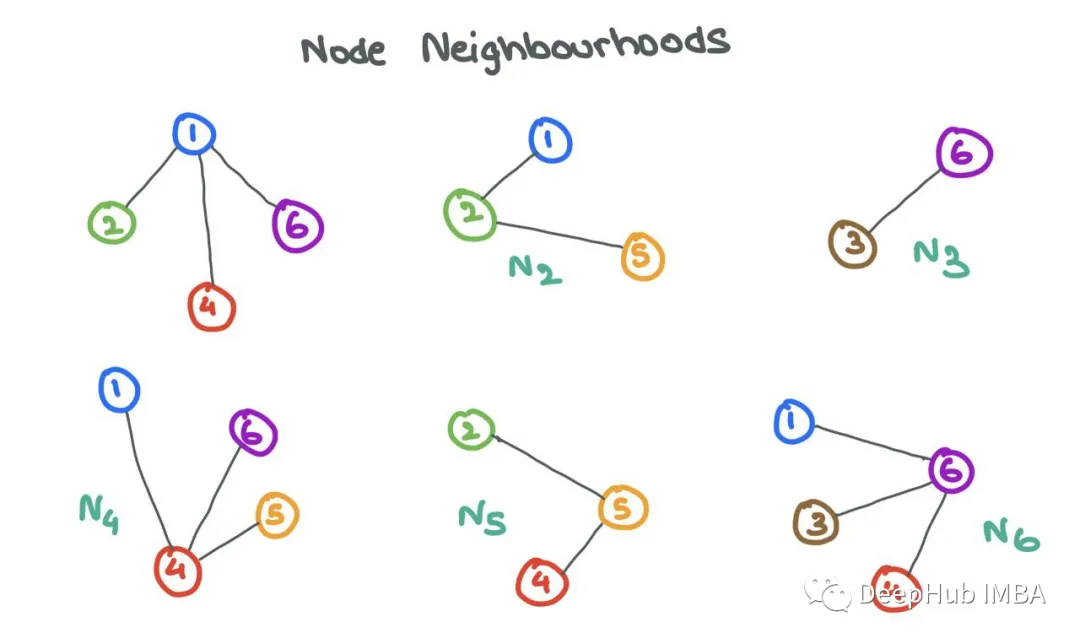
A person is influenced by the circles they are in. Similarly, GNN can learn a lot about node i by looking at the nodes in its neighborhood Ni. To implement this information sharing between the source node i and its neighboring nodes j, GNN performs message passing.

For a GNN layer, message passing is defined as the process of obtaining the features of neighboring nodes, transforming them, and “passing” them to the source node. This process is repeated in parallel for all nodes in the graph. Thus, at the end of this step, all neighborhoods will have been checked.

Let’s zoom in on node 6 and examine its neighborhood N6 = {1,3,4}. We take each node feature x1, x3, and x4, and transform them using a function F, which can be a simple neural network (MLP or RNN) or an affine transformation F(xj) = Wj⋅xj + b. Simply put, the “message” is the transformed node features from the source node.

F can be a simple affine transformation or a neural network. Now we set F(xj) = Wj⋅xj for convenience of calculation, where ⋅ represents simple matrix multiplication.

Aggregation

Now that we have the transformed messages {F(x1), F(x3), F(x4)} passed to node 6, we need to aggregate (i.e., “combine”) them in some way. There are many ways to combine them. Common aggregation functions include:

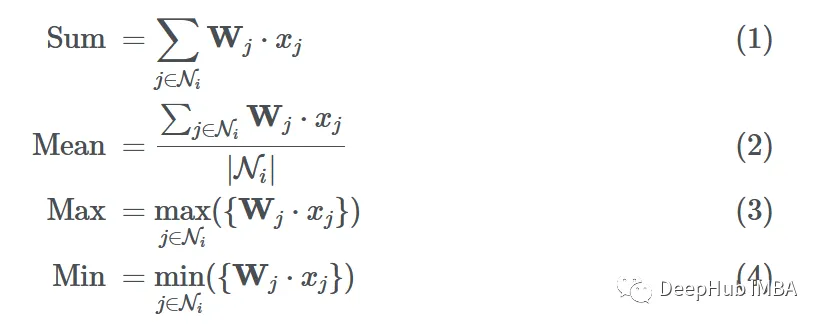
Assuming we use a function G to aggregate the messages from neighbors (using sum, mean, max, or min), the final aggregated message can be expressed as:

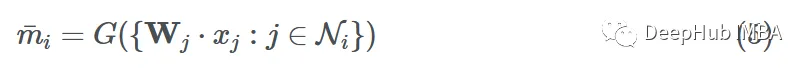
Update

Using these aggregated messages, the GNN layer updates the features of the source node i. At the end of this update step, the node should know not only itself but also its neighbors. This is done by taking the feature vector of node i and combining it with the aggregated message, which can be done with a simple addition or concatenation operation.

Using addition

where σ is an activation function (ReLU, ELU, Tanh), H is a simple neural network (MLP) or affine transformation, and K is another MLP that projects the addition vector into another dimension.

Using concatenation:

To further abstract this update step, we can view K as some projection function that transforms the message and the source node embedding together:

The initial node features are referred to as xi, and after passing through the first GNN layer, we transform the node features to hi. Assuming we have more GNN layers, we can denote the node features as hli, where l is the index of the current GNN layer. Similarly, it is clear that h0i = xi (i.e., the input to the GNN).

Putting It All Together

Now that we have completed the message passing, aggregation, and update steps, let’s put them together to form a single GNN layer on a single node i:

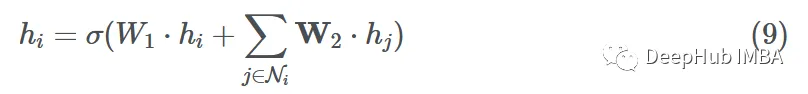
Here we use sum aggregation and a simple feedforward layer as the functions F and H. Let hi ∈ Rd, W1, W2 ⊆ Rd’ × d where d’ is the embedding dimension.

Using the Adjacency Matrix

So far, we have observed the entire forward pass of the GNN from the perspective of a single node i. Knowing how to implement the GNN forward pass when given the entire adjacency matrix A and all node features in X ⊆ RN × d is also essential.

In the MLP forward pass, we want to weight the items in the feature vector xi. This can be seen as the dot product of the node feature vector xi ∈ Rd and the parameter matrix W ⊆ Rd’ × d, where d’ is the embedding dimension:

If we want to do this for all samples in the dataset (vectorized), we can simply multiply the parameter matrix with the feature matrix to obtain the transformed node features (messages):

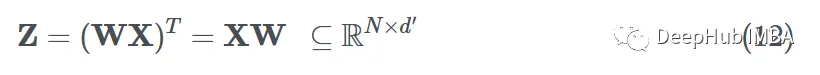
In GNN, for each node i, the message aggregation operation includes obtaining the feature vectors of neighboring nodes, transforming them, and adding them together (in the case of sum aggregation).

For a single row Ai, for each index j where Aij = 1, we know that nodes i and j are connected → eij ∈ E. For instance, if A2 = [1, 0, 1, 1, 0], we know that node 2 is connected to nodes 1, 3, and 4. Therefore, when we multiply A2 with Z = XW, we only consider columns 1, 3, and 4, while ignoring columns 2 and 5:

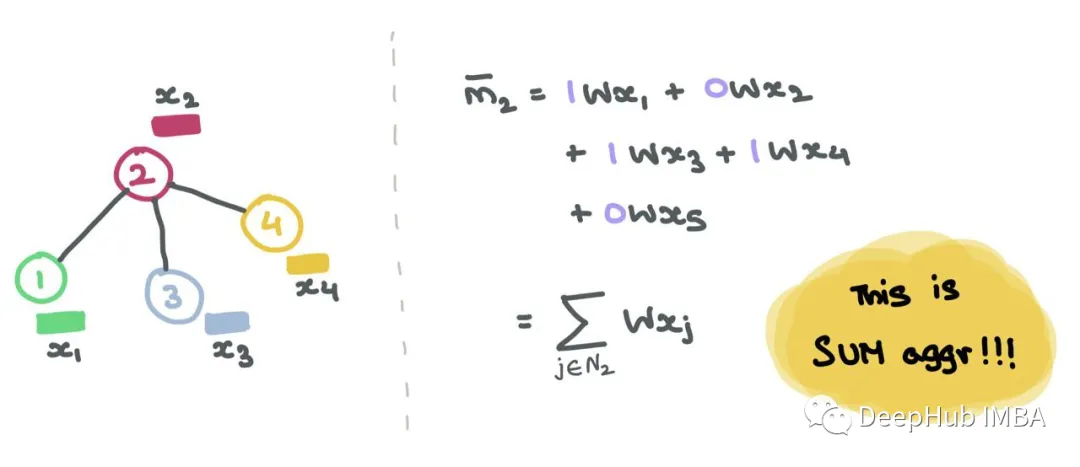
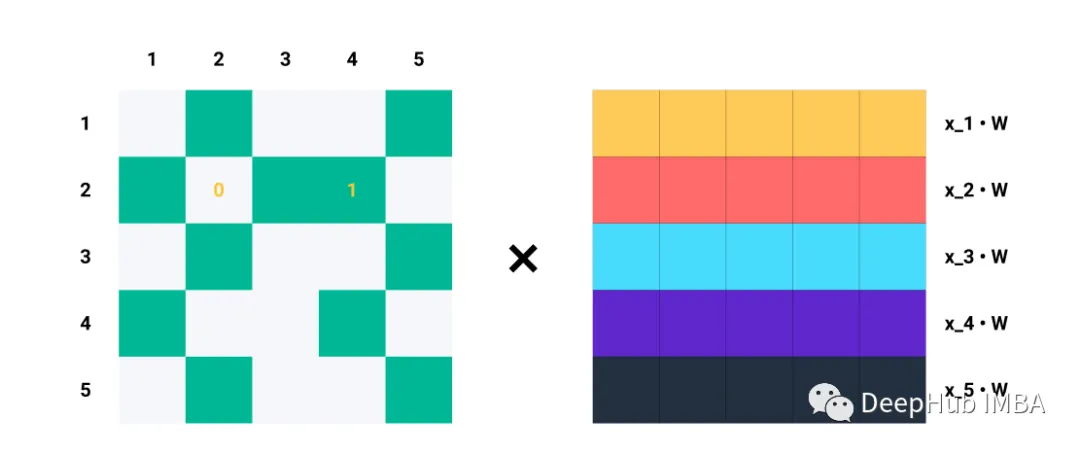
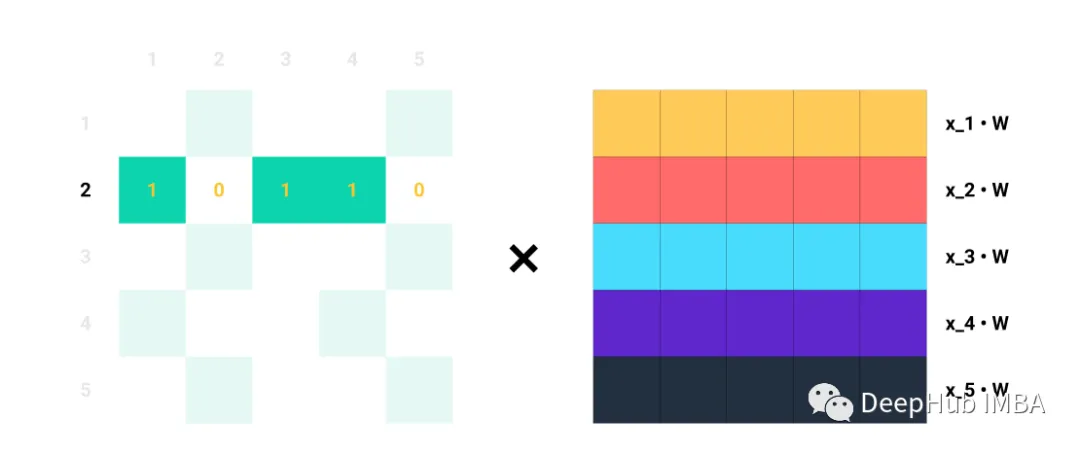
For example, the second row of A.

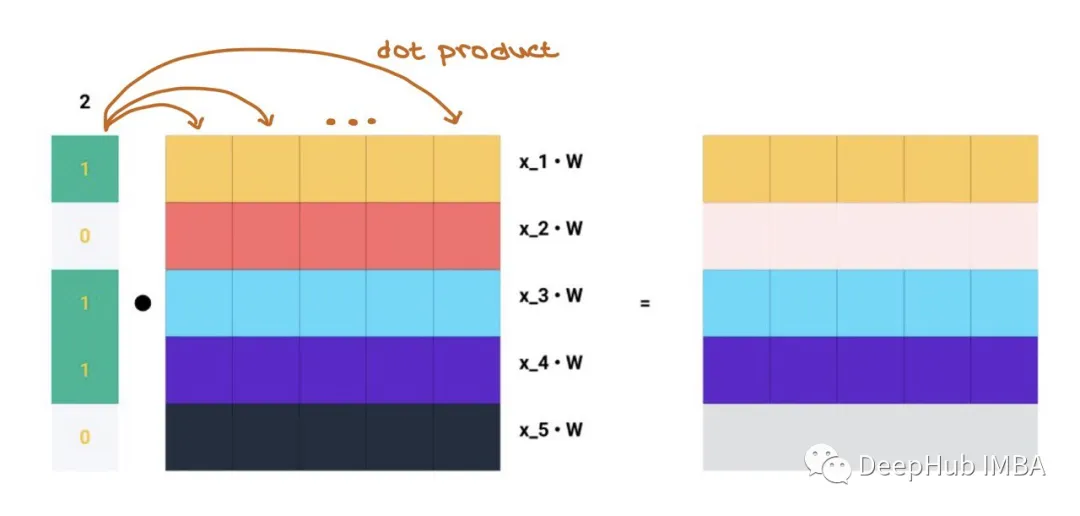
Matrix multiplication is the dot product of each row in A with each column in Z, which is what message aggregation means!!

To obtain the aggregated messages for all N, we perform matrix multiplication of the entire adjacency matrix A with the transformed node features based on the connections between nodes in the graph:

However, there is a small issue: the observed aggregated messages do not consider the feature vector of node i itself (as we did above). So we will add self-loops to A (each node i connects to itself).

This means that the diagonal values need to be modified, and with some linear algebra, we can do this using the identity matrix!

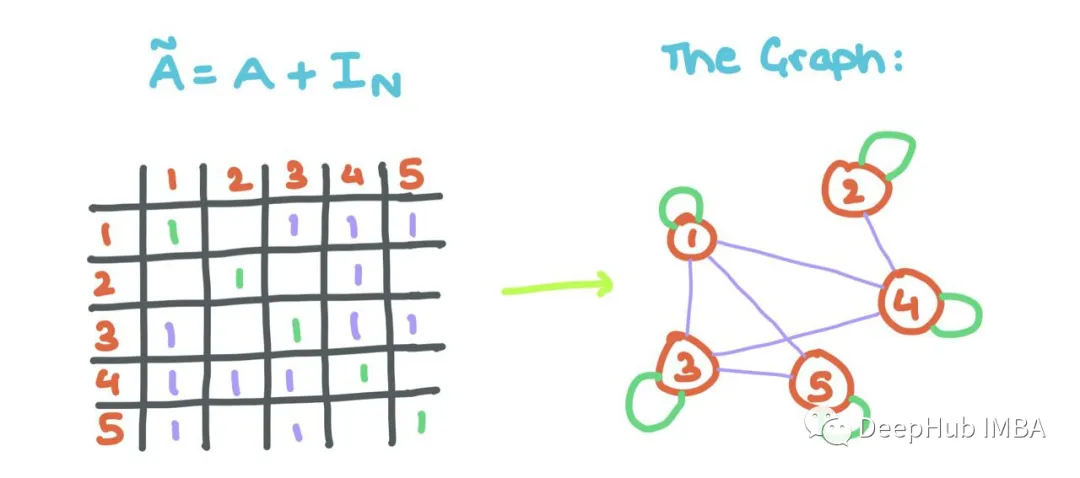
Adding self-loops allows GNN to aggregate the features of the source node along with the features of its neighboring nodes!!

With this, you can implement the GNN pass using matrices instead of single nodes.

⭐ To perform mean aggregation, we can simply divide the total sum by 1. For the above example, since there are three 1s in A2 = [1, 0, 0, 1, 1], we can divide ∑j∈N2Wxj by 3. However, it is not possible to implement max (max) and min aggregation (min) using the GNN adjacency matrix formula.

Stacking GNN Layers

Now that we have introduced how a single GNN layer works, how do we use these layers to construct an entire “network”? How does information flow between layers, and how does GNN refine the embeddings/representations of nodes (and/or edges)?

• The input to the first GNN layer is the node features X ⊆ RN × d. The output is intermediate node embeddings H1 ⊆ RN × d1, where d1 is the embedding dimension of the first layer. H1 consists of h1i: 1 → N ∈ Rd1.

• H1 is the input to the second layer. The next output is H2 ⊆ RN × d2, where d2 is the embedding dimension of the second layer. Similarly, H2 consists of h2i: 1 → N ∈ Rd2.

• After several layers, at the output layer L, the output is HL ⊆ RN × dL. Finally, HL consists of hLi: 1 → N ∈ RdL.

The choice of {d1, d2, …, dL} is entirely up to us and can be seen as hyperparameters of the GNN. These can be thought of as the number of units (“neurons”) chosen for the MLP layers.

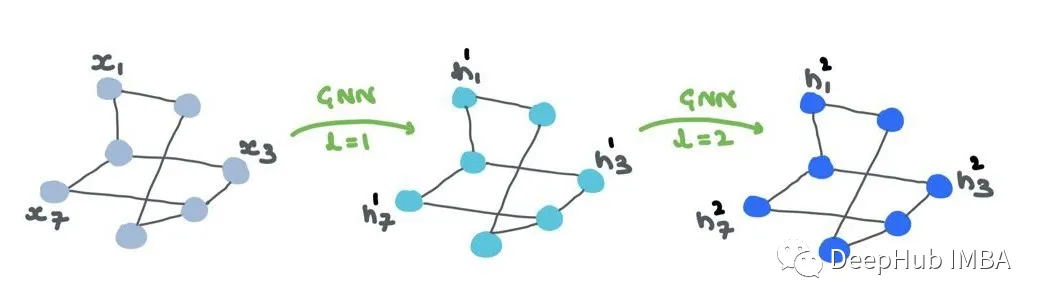
Node features/embeddings (“representations”) are passed through the GNN. While the structure remains unchanged, the node representations continuously change across layers. Edge representations will also change, but the connections or directions will not change.

HL can also do several things:

We can sum it along the first axis (i.e., ∑Nk=1hLk) to obtain a vector in RdL. This vector is the latest dimensional representation of the entire graph. It can be used for graph classification (e.g., what molecule is this?)

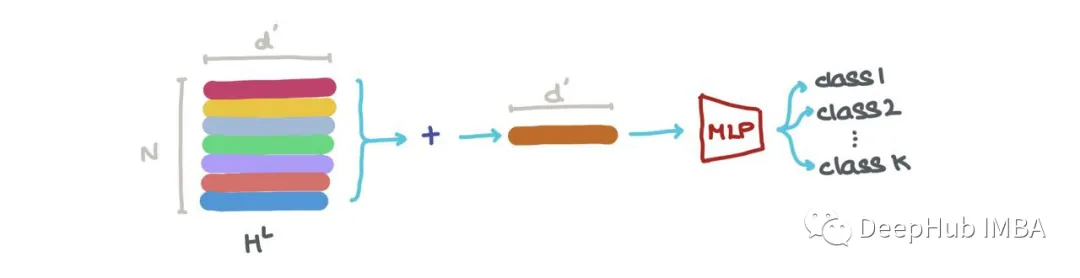
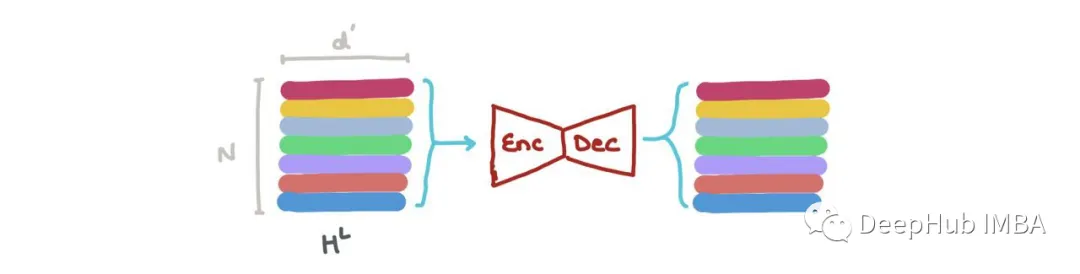
We can concatenate the vectors in HL (i.e., ⨁Nk=1hk, where ⊕ is the vector concatenation operation) and pass it to a Graph Autoencoder. This operation is needed when the input graph has noise or is corrupted, and we want to reconstruct a denoised graph.

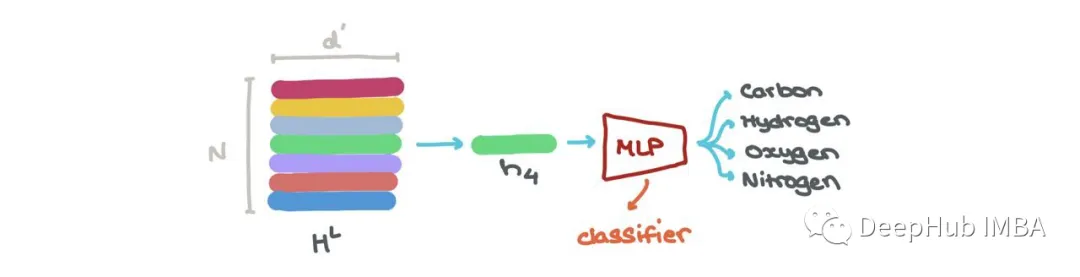
We can perform node classification → what class does this node belong to? The node embedded at a specific index hLi (i: 1 → N) can be classified into K classes (e.g., is this a carbon atom, hydrogen atom, or oxygen atom?) using a classifier (like MLP).

We can also perform link prediction → is there a link between nodes i and j? The node embeddings hLi and hLj can be input into another sigmoid-based MLP, which outputs the probability that there is an edge between these nodes.

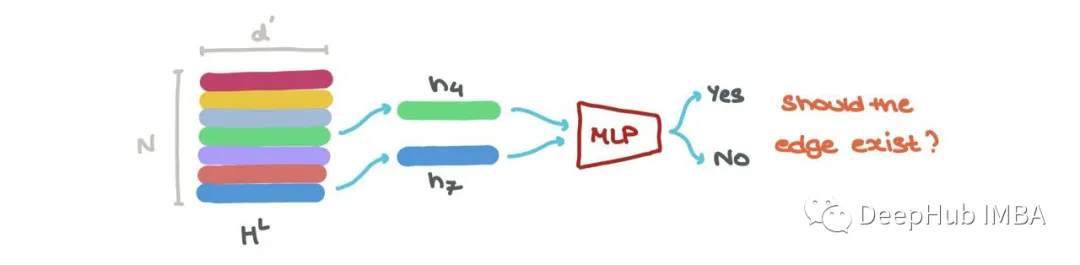
These are the operations that GNN performs in different applications. In any case, each h1 → N ∈ HL can be stacked and treated as a batch of samples. We can easily treat it as a batch process.

For a given node i, the GNN aggregated layer l has the l-hop neighborhood of node i. The node sees its immediate neighbors and reaches deeper into the network, interacting with its neighbors’ neighbors.

This is why, for very small, sparse graphs (with few edges), a large number of GNN layers often leads to performance degradation: because node embeddings converge to a single vector, as each node sees many nodes far away. For small graphs, this is of no use.

This also explains why most GNN papers often use ≤4 layers in experiments to prevent the network from encountering issues.

Training GNN with Node Classification as an Example

During training, predictions for nodes, edges, or the entire graph can be compared to ground-truth labels from the dataset using a loss function (e.g., cross-entropy). In other words, GNN can be trained in an end-to-end manner using backpropagation and gradient descent.

Training and Testing Data

Like conventional ML, graph data can also be split into training and testing. There are two methods:

1. Transductive

Training and testing data are in the same graph. Nodes in each set are interconnected. Only during training are the labels of the test nodes hidden while the labels of the training nodes are visible. However, the features of all nodes are visible to the GNN.

We can apply a binary mask to all nodes (if a training node i is connected to a test node j, simply set Aij = 0 in the adjacency matrix).

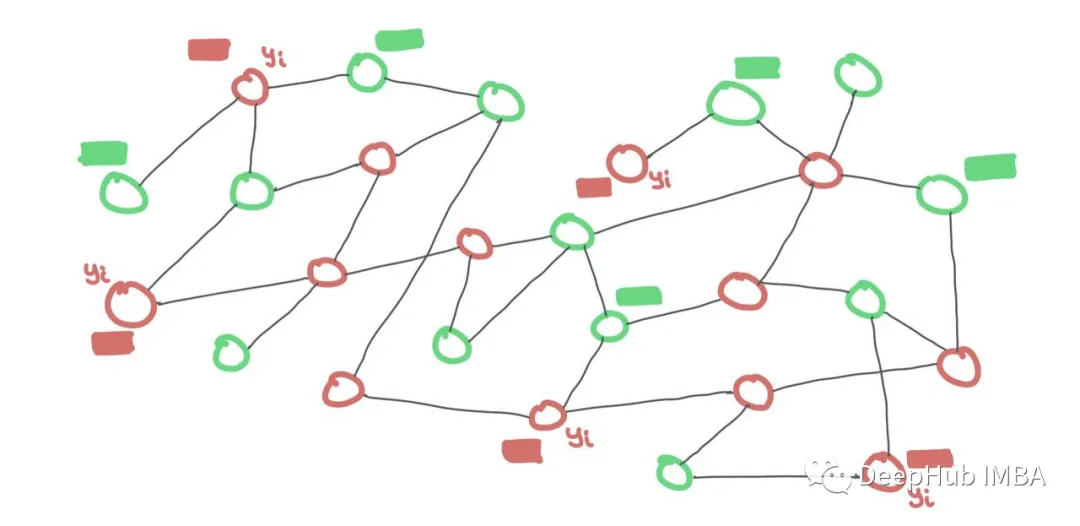
Both training and testing nodes are part of the same graph. Training nodes expose their features and labels, while testing nodes only expose their features. The test labels are hidden from the model. A binary mask is needed to inform the GNN which nodes are training nodes and which are testing nodes.

2. Inductive

The other method involves separate training and testing graphs. This is similar to conventional ML, where the model only sees features and labels during training, and only sees features for testing. Training and testing are conducted on two independent graphs. These testing graphs are distributed externally to check the generalization quality during training.

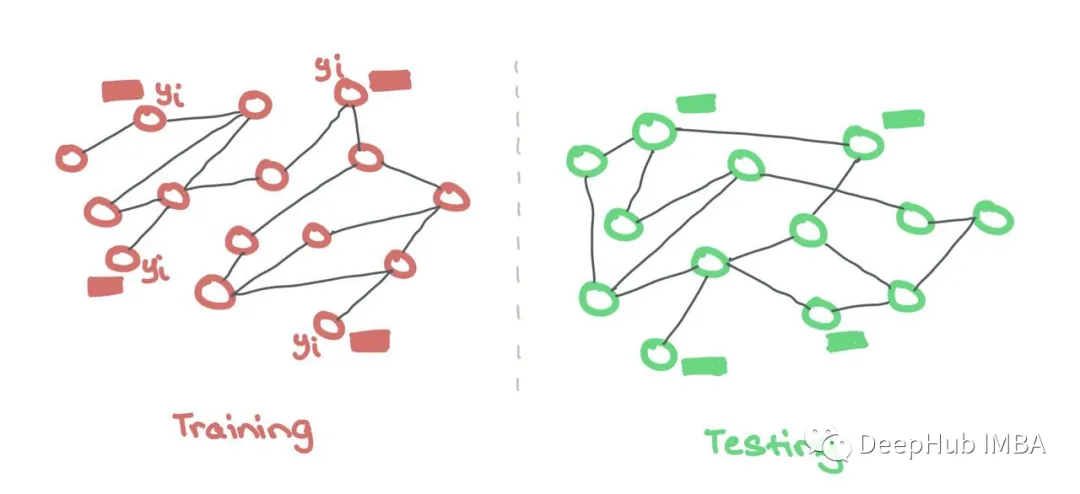
Like conventional ML, training and testing data are stored separately. GNN only uses features and labels from training nodes. There is no need for a binary mask to hide testing nodes, as they come from different sets.

Backpropagation and Gradient Descent

During training, once we pass forward through the GNN, we obtain the final node representation hLi ∈ HL. To train in an end-to-end manner, we can do the following:

• Input each hLi into an MLP classifier to obtain predictions ^yi

• Calculate loss using ground-truth yi and predictions yi → J(yi, yi)

• Use backpropagation to compute ∂J/∂Wl, where Wl is the parameter matrix from layer l

• Use an optimizer to update the parameters Wl of each layer in the GNN

• (if needed) can also fine-tune the weights of the classifier (MLP) network.

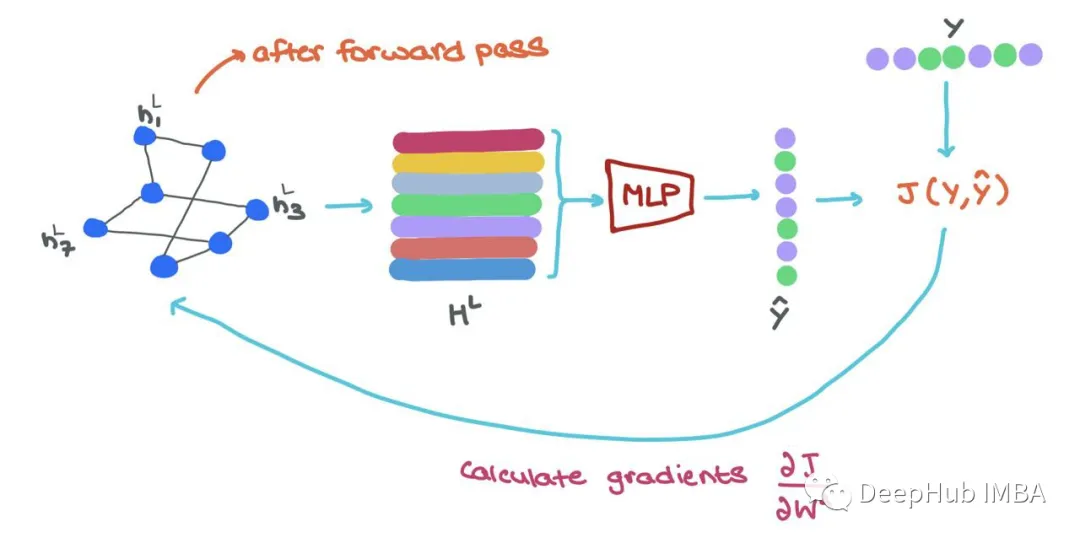
🥳 This means that GNN is easy to parallelize in both message passing and training. The entire process can be vectorized (as shown above) and executed on a GPU!!

Summary of Popular Graph Neural Networks

Above we have introduced the basic process of ancient neural networks, and now we summarize popular Graph Neural Networks and break down their equations and mathematics into the three GNN steps mentioned above. Many architectures combine the message passing and aggregation steps into a single function instead of explicitly performing them one after the other, but for mathematical convenience, we will attempt to decompose them and treat them as a single operation!

1. Message Passing Neural Networks

https://arxiv.org/abs/1704.01212

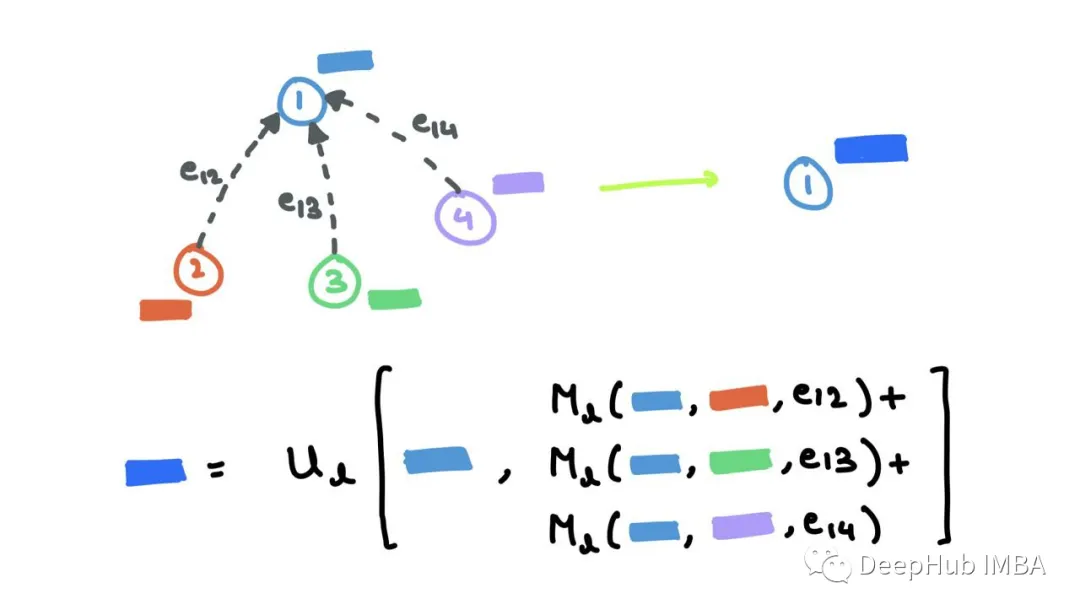
Message Passing Neural Networks (MPNN) decomposes the forward pass into a message passing phase with a message function Ml and a readout phase with a vertex update function Ul.

MPNN combines the message passing and aggregation steps into a single message passing phase:

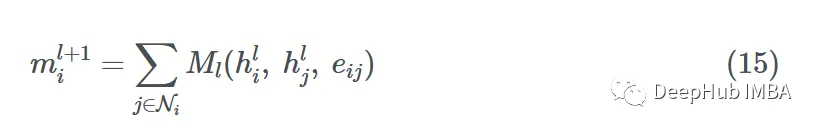
The readout phase is the update step:

where ml+1v is the aggregated message, hl+1v is the updated node embedding. This is very similar to the process I mentioned above. The message function Ml is a mixture of F and G, and the function Ul is k, where eij represents possible edge features, which can also be omitted.

2. Graph Convolution

https://arxiv.org/abs/1609.02907

Graph Convolutional Networks (GCN) papers study the entire graph in the form of an adjacency matrix. Self-connections are added to the adjacency matrix to ensure all nodes connect to themselves to obtain ~A. This ensures that the embeddings of the source nodes are considered during the message aggregation. The combined message aggregation and update step is shown below:

where Wl is a learnable parameter matrix. Here, X is changed to H to generalize the node features on any layer l, where H0 = X.

Due to the associative property of matrix multiplication (A(BC) = (AB)C), it does not matter in which sequence we multiply the matrices (either ~AHl is multiplied first and then Wl, or HlWl is multiplied first and then ~A). The authors Kipf and Welling further introduced the degree matrix ~D as a form of