Original link:https://medium.com/towards-artificial-intelligence/one-lego-at-a-time-explaining-the-math-of-how-neural-networks-learn-with-implementation-from-scratch-39144a1cf80
From:Yongyu
Excerpted from Algorithm Notes
https://github.com/omar-florez/scratch_mlp/
The author explains step by step the mathematical processes used in training a neural network from scratch.
Neural networks are cleverly arranged linear and nonlinear modules.
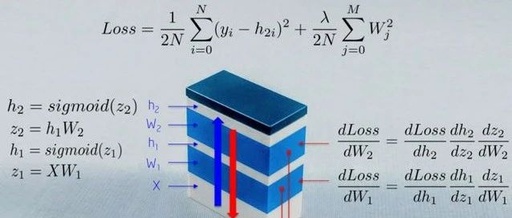
The above image describes some of the mathematical processes involved in training a neural network. We will explain this in the article. One interesting point for readers is that a neural network is a stack of many modules with different objectives.
-
The input variable X feeds raw data into the neural network, stored in a matrix where the rows are observations and the columns are dimensions.
-
Weights W_1 map input X to the first hidden layer h_1. The weights W_1 serve as a linear kernel.
-
The Sigmoid function prevents numbers in the hidden layer from falling outside the range of 0-1. The result is an array of neural activations, h_1 = Sigmoid(WX).
At this point, these operations only form a general linear system and cannot model nonlinear interactions. This changes when we add another layer, increasing the depth of the module’s structure. The deeper the network, the more subtle nonlinear interactions we learn, and the more complex problems we can solve, which may be one of the reasons for the rise of deep neural models.
Why should I read this article?
If you understand the internal parts of a neural network, you will quickly know where to change when encountering problems and can devise strategies to test the invariants and expected behaviors of the parts of the algorithm you know.
Debugging machine learning models is a complex task. In practice, mathematical models often do not work on the first attempt. They may yield low accuracy on new data, take a long time to train, consume too much memory, or return large negative values or NAN predictions… In some cases, understanding how the algorithm operates can make our tasks much easier:
-
If training takes too long, increasing the minibatch size might be a good idea, as it can reduce the variance of observations and help the algorithm converge.
-
If you see NAN predictions, the algorithm may have received large gradients, causing memory overflow. This can be seen as a matrix multiplication that explodes after many iterations. Reducing the learning rate can shrink these values. Reducing the number of layers can decrease the number of multiplications. Gradient clipping can also significantly control this issue.
Specific example: Learning the XOR function
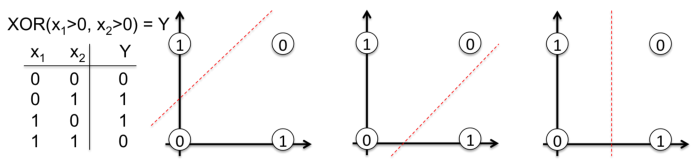
Let’s open the black box. We will now build a neural network to learn a function from scratch. Choosing this nonlinear function is certainly not random. Without backpropagation, it is hard to learn to classify with a straight line.
To describe this important concept, note in the following image why a straight line cannot classify the outputs of the XOR function into 0 and 1. Real-world problems are also nonlinearly separable.
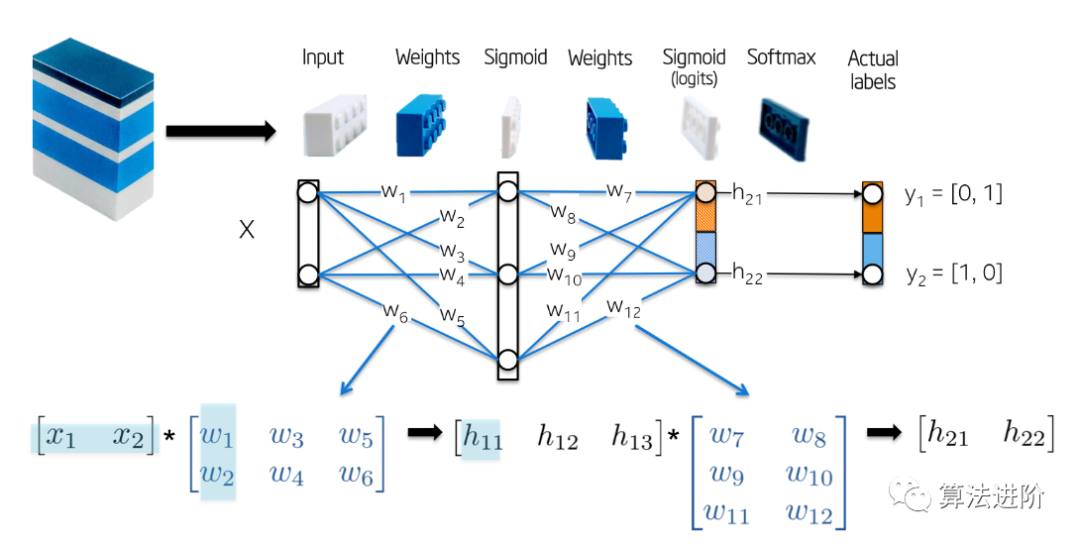
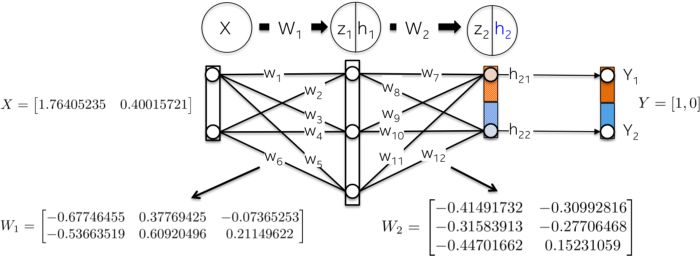
The topology of this network is very simple:
-
The input variable X is a two-dimensional vector.
-
The weights W_1 are a 2×3 matrix with randomly initialized values.
-
The hidden layer h_1 contains 3 neurons. Each neuron receives the weighted sum of the observations as input, represented by the green-highlighted inner product in the image: z_1 = [x_1, x_2][w_1, w_2].
-
The weights W_2 are a 3×2 matrix with randomly initialized values.
-
The output layer h_2 contains two neurons because the XOR function outputs either 0 (y_1=[0,1]) or 1 (y_2 = [1,0]).
The following image provides a more intuitive view:
Now let’s train this model. In our simple example, the trainable parameters are the weights, but it should be noted that current research is exploring more types of parameters that can be optimized, such as shortcut connections between layers, distributions, topologies, residuals, learning rates, etc.
Backpropagation is a method that updates the weights in the direction of minimizing a predefined error metric (the loss function) on a given batch of labeled observations. This algorithm has been rediscovered multiple times; it is a special case of a more general technique known as automatic differentiation in reverse accumulation mode.
Network Initialization
Let’s initialize the network weights with random numbers.
Forward Step:
The goal of this step is to propagate the input variable X forward through each layer of the network until calculating the output layer h_2 vector.
Here are the calculations that occur:
Using weights W_1 as a linear kernel, perform a linear transformation on the input data X:
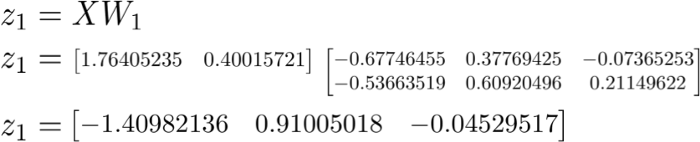
Using the Sigmoid activation function to scale the weighted sum gives the value of the first hidden layer h_1. Note that the original 2D vector is now mapped to 3D space.

A similar process occurs in layer h_2. First, we calculate the weighted sum z_2, which is now the input data.

Then we compute their Sigmoid activation function. The vector [0.37166596 0.45414264] represents the log probabilities or prediction vector calculated by the network for the given input X.

Calculating Overall Loss
Also known as “actual value minus predicted value,” the purpose of this loss function is to quantify the distance between the prediction vector h_2 and the artificial labels y.
Note that this loss function includes a regularization term that penalizes large weights in the form of ridge regression. In other words, weights with larger squared values increase the loss function, which is the metric we want to minimize.
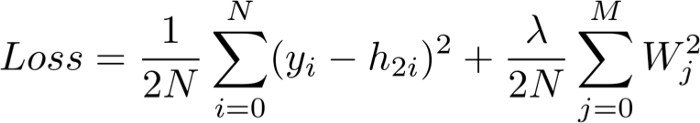
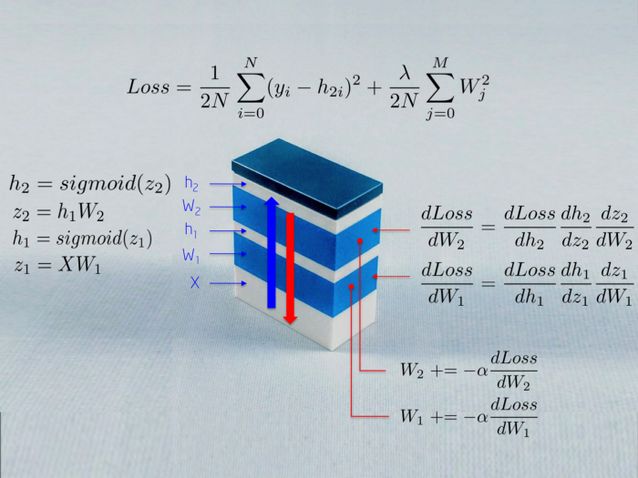
Backward Step:
The goal of this step is to update the weights of the neural network in the direction of minimizing the loss function. As we will see, this is a recursive algorithm that reuses previously computed gradients and heavily relies on differential functions. Since these updates reduce the loss function, a neural network “learns” to approximate the labels of observations with known categories. This is an attribute known as generalization.
Unlike the forward step, this step proceeds in reverse order. It first computes the partial derivative of the loss function with respect to each weight in the output layer (dLoss/dW_2), and then computes the partial derivatives for the hidden layer (dLoss/dW1). Let’s explain each derivative in detail.
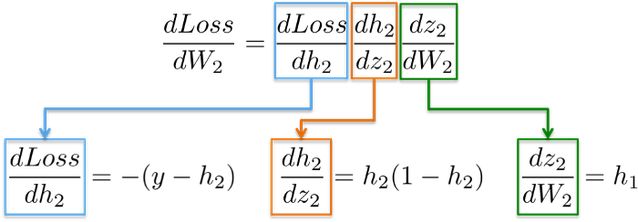
dLoss/dW_2:
The chain rule indicates that we can decompose the gradient calculation of a neural network into multiple differential parts:
To aid memory, the following table lists some function definitions used above and their first derivatives:
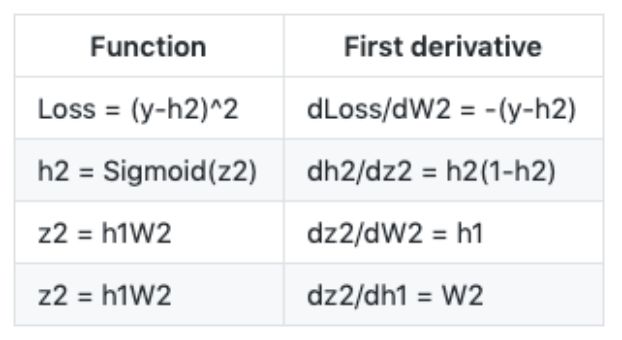
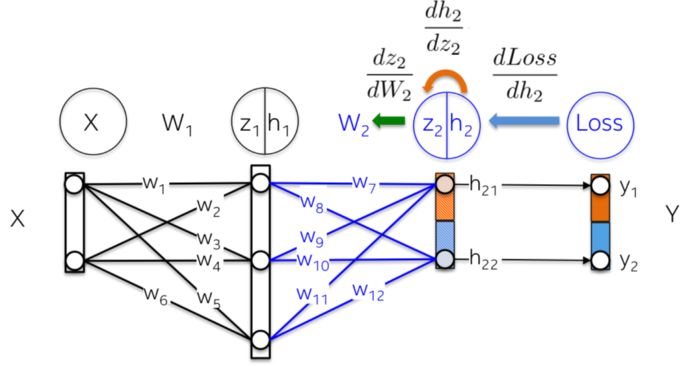
More intuitively, in the following image, we will update weights W_2 (blue part). To do this, we need to calculate three partial derivatives along the derivative chain.
By substituting the values into these partial derivatives, we can compute the partial derivative of W_2 as follows:
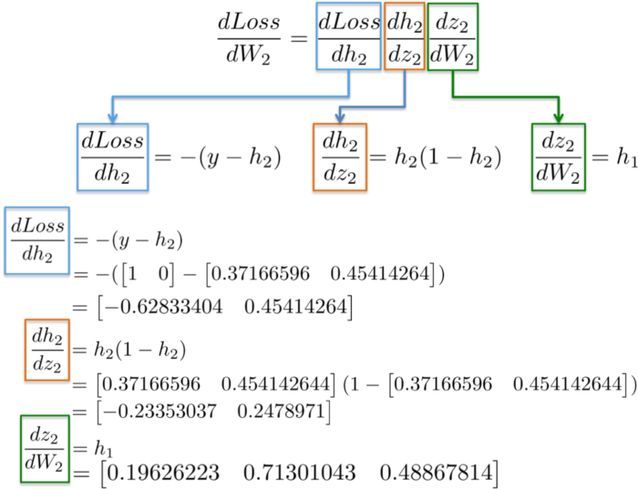
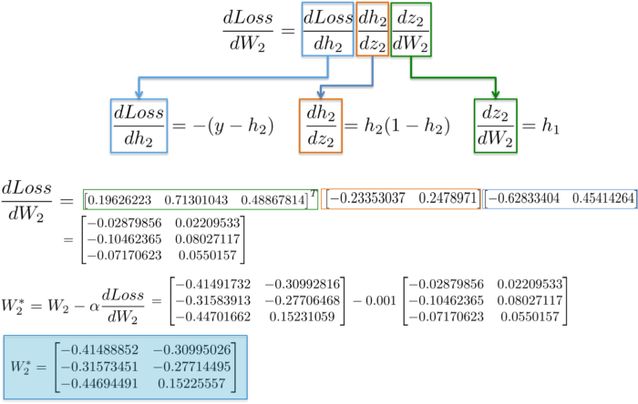
The result is a 3×2 matrix dLoss/dW_2, which will update the values of W_2 in the direction of minimizing the loss function.
dLoss/dW_1:
The chain rule used to update the weights of the first hidden layer W_1 demonstrates the potential for reusing previously computed results.
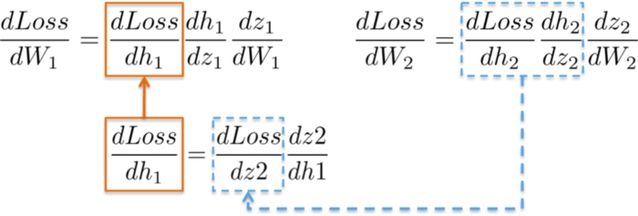
More intuitively, the path from the output layer to the weights W_1 will encounter previously computed partial derivatives from later layers.

For example, the partial derivatives dLoss/dh_2 and dh_2/dz_2 have already been computed as dependencies for the output layer dLoss/dW_2 learning weights.
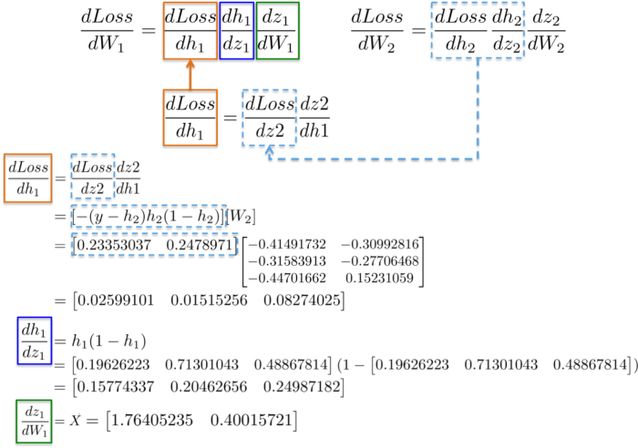
By putting all the derivatives together, we can once again apply the chain rule to update the weights for the hidden layer W_1.

Finally, we assign new values to the weights, completing one step of training for the neural network.
Implementation
Let’s use numpy as a linear algebra engine to convert the above mathematical equations into code. The neural network is trained in a loop, where each iteration presents the neural network with standard input data.
In this small example, we consider the entire dataset in each iteration. The calculations of the forward step, loss function, and backward step yield good generalization because we use their corresponding gradients (matrices dL_dw1 and dL_dw2) to update the trainable parameters in each cycle.
Code is stored in this repo: https://github.com/omar-florez/scratch_mlp

Let’s run this code!
Below are some neural networks that have been trained over many iterations to approximate the XOR function.
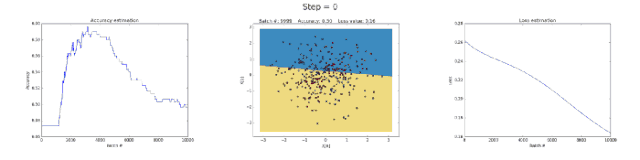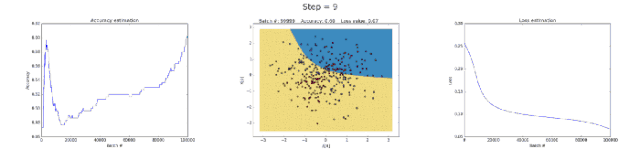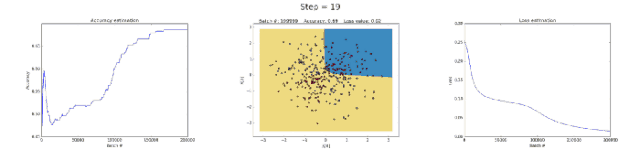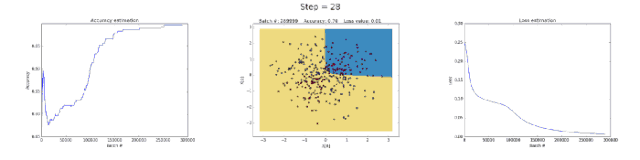
Left image: accuracy; middle image: learned decision boundary; right image: loss function
First, let’s look at why a neural network with 3 neurons in the hidden layer has limited capability. This model learned to perform binary classification with a simple decision boundary that started as a straight line but later exhibited nonlinear behavior. As training continued, the loss function in the right image clearly decreased.
The neural network with 50 neurons in the hidden layer significantly increased the model’s ability to learn complex decision boundaries. Not only did it achieve more accurate results, but it also caused the gradients to explode, which is a significant issue when training neural networks. When the gradients are very large, the backpropagation will produce substantial updates to the weights. This is why the loss function suddenly increased during the last few training steps (step>90). The regularization term of the loss function calculated the squared values of the weights that had become very large (sum(W²)/2N).
As you can see, this problem can be avoided by reducing the learning rate. This can be achieved by implementing a strategy that decreases the learning rate over time. Alternatively, a stronger regularization can be enforced, possibly L1 or L2. Gradient vanishing and gradient explosion are interesting phenomena that we will analyze comprehensively later.
—END—