Selected by OpenAI
Author: JAKOB FOERSTER
Translation by Machine Heart
Using linear networks for nonlinear computation is an unconventional approach. Recently, OpenAI published a blog introducing their new research on deep linear networks, which do not use activation functions, yet achieve 99% training accuracy and 96.7% testing accuracy on MNIST. This new research has reignited discussions. Let’s see how they did it.
We demonstrate that deep linear networks (implemented with floating-point operations) are not actually linear; they can perform nonlinear computations. We leverage this by using evolutionary strategies to find parameters in linear networks, allowing us to solve significant problems.
Neural networks are typically composed of a stack of linear layers and nonlinear functions (like tanh and ReLU). Without nonlinearity, a series of linear layers is theoretically equivalent to a single linear layer. Thus, floating-point operations are nonlinear enough to train deep networks. This is surprising.
Background
The numbers used by computers are not perfect mathematical objects; they are approximate representations using a finite number of bits. Floating-point numbers are commonly used by computers to represent mathematical objects. Each floating-point number consists of a combination of a fraction and an exponent. In the IEEE float32 standard, the fraction is allocated 23 bits, the exponent is allocated 8 bits, and there is one bit for the sign.

According to this convention and binary format, the smallest non-zero normal number represented in binary is 1.0..0 x 2^-126, referred to as min. The next representable number is 1.0..01 x 2^-126, which can be written as min + 0.0..01 x 2^-126. Clearly, the gap between the first and second numbers is 2^20 times smaller than the gap between 0 and min. In the float32 standard, when a number is smaller than the smallest representable number, it is mapped to zero. Therefore, all computations involving floating-point numbers near zero will be nonlinear (except for denormal numbers, which may not be available on some computational hardware. In our case, we address this issue by setting flush to zero (FTZ), treating all denormal numbers as zero).
Thus, while the distinction between all numbers and their floating-point representations is usually small, a large gap occurs near zero, and this approximation error can have significant effects.
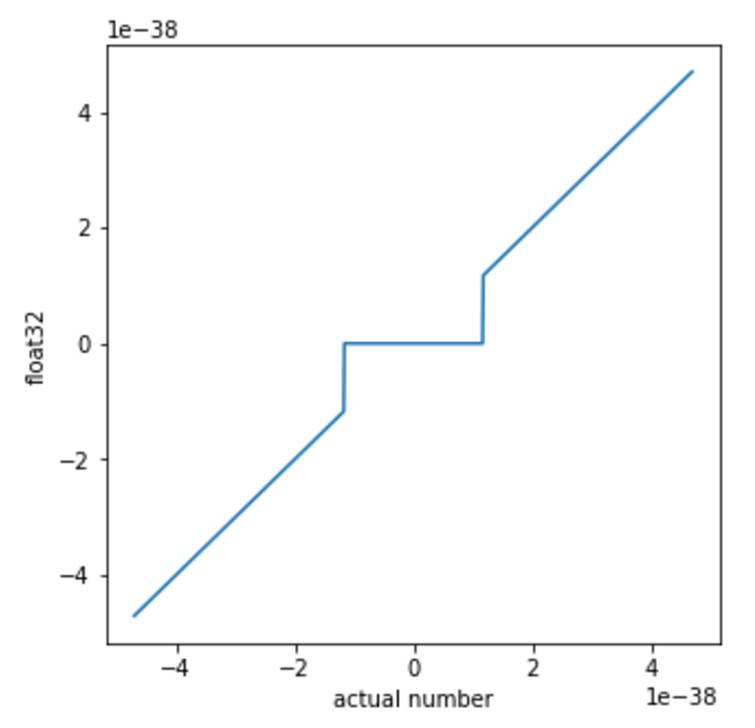
This can lead to some strange effects where common mathematical rules fail. For example, (a + b) x c does not equal a x c + b x c.
For instance, if you set a = 0.4 x min, b = 0.5 x min, c = 1 / min.
-
Then: (a+b) x c = (0.4 x min + 0.5 x min) x 1 / min = (0 + 0) x 1 / min = 0.
-
However: (a x c) + (b x c) = 0.4 x min / min + 0.5 x min x 1 / min = 0.9.
Similarly, we can set a = 2.5 x min, b = -1.6 x min, c = 1 x min.
-
Then: (a+b) + c = (0) + 1 x min = min
-
However: (b+c) + a = (0 x min) + 2.5 x min = 2.5 x min.
In such small scales, basic addition becomes nonlinear!
Using Evolutionary Strategies to Leverage Nonlinearity
We wanted to know if this inherent nonlinearity could be utilized as a method for computing nonlinearity. If so, deep linear networks could perform nonlinear operations. The challenge is that modern differentiation libraries tend to ignore them when the nonlinear scale is small. Therefore, using backpropagation to exploit nonlinearity for training neural networks is difficult or impossible.
We can use evolutionary strategies (ES), which can evaluate gradients without relying on symbolic differentiation. By using evolutionary strategies, we can treat the near-zero behavior of float32 as a method for computing nonlinearity. When trained on the MNIST dataset, deep linear networks achieve 94% training accuracy and 92% testing accuracy (Machine Heart achieved 98.51% testing accuracy with a three-layer fully connected network). In contrast, the same linear network trained with evolutionary strategies achieves over 99% training accuracy and 96.7% testing accuracy, ensuring the activation values are sufficiently small and distributed within the nonlinear range of float32. The improvement in training performance is due to using the nonlinear evolutionary strategies in the float32 representation. These powerful nonlinearities allow arbitrary layers to generate new features that are nonlinear combinations of lower-level features. Here is the network structure:
x = tf.placeholder(dtype=tf.float32, shape=[batch_size,784])
y = tf.placeholder(dtype=tf.float32, shape=[batch_size,10])
w1 = tf.Variable(np.random.normal(scale=np.sqrt(2./784),size=[784,512]).astype(np.float32))
b1 = tf.Variable(np.zeros(512,dtype=np.float32))
w2 = tf.Variable(np.random.normal(scale=np.sqrt(2./512),size=[512,512]).astype(np.float32))
b2 = tf.Variable(np.zeros(512,dtype=np.float32))
w3 = tf.Variable(np.random.normal(scale=np.sqrt(2./512),size=[512,10]).astype(np.float32))
b3 = tf.Variable(np.zeros(10,dtype=np.float32))
params = [w1,b1,w2,b2,w3,b3]
nr_params = sum([np.prod(p.get_shape().as_list()) for p in params])
scaling = 2**125
def get_logits(par):
h1 = tf.nn.bias_add(tf.matmul(x , par[0]), par[1]) / scaling
h2 = tf.nn.bias_add(tf.matmul(h1, par[2]) , par[3] / scaling)
o = tf.nn.bias_add(tf.matmul(h2, par[4]), par[5]/ scaling)*scaling
return o
In the code above, we can see that the network has a total of 4 layers, with the first layer having 784 (28*28) input neurons, which must match the number of pixels in a single image from the MNIST dataset. The second and third layers are hidden layers, each with 512 neurons, and the final layer has 10 output categories. The fully connected weights between each pair of layers are initialized randomly following a normal distribution. nr_params is the cumulative product of all parameters. Below is the definition of the get_logist() function, where the input variable par should match the previously defined nr_params, as the indices for adding bias terms are 1, 3, 5, which exactly corresponds to the previously defined nr_params, but OpenAI did not provide the calling process for this function. The first expression in the function calculates the forward propagation result between the first and second layers, i.e., it computes the product of input x and w1, adding the scaled bias term (previously defined b1, b2, b3 as zero vectors). The subsequent two calculations are also similar, with the final output o being the predicted category for image recognition. However, OpenAI only provided the network architecture and did not include optimization methods or loss functions.
Besides validating MNIST, OpenAI believes that other experiments could extend this work to recurrent neural networks or leverage nonlinear computations to enhance performance in complex machine learning tasks, such as language modeling and translation. OpenAI stated that they will continue to advance this direction in the future.
Original article link: https://blog.openai.com/nonlinear-computation-in-linear-networks/
This article is a translation by Machine Heart. Please contact this public account for authorization to reproduce..
✄————————————————
Join Machine Heart (Full-time Reporter/Intern): [email protected]
Submissions or Coverage Requests: [email protected]
Advertising & Business Cooperation: [email protected]
