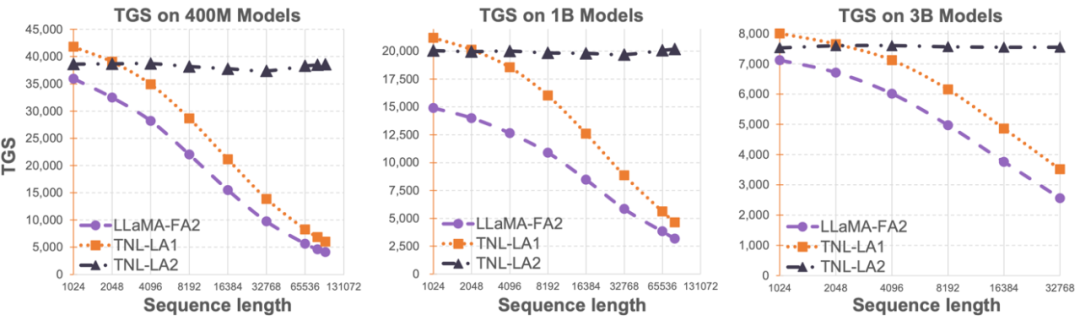
Lightning Attention-2: Unlimited Sequence Lengths with Constant Compute Cost

Lightning Attention-2 is a novel linear attention mechanism that aligns the training and inference costs of long sequences with those of a 1K sequence length.

The limitations on sequence length in large language models significantly constrain their applications in artificial intelligence, such as multi-turn dialogue, long text understanding, and the processing and generation of multimodal data. The fundamental reason for this limitation lies in the quadratic computational complexity relative to sequence length inherent in the Transformer architecture adopted by current large language models. This means that as the sequence length increases, the required computational resources increase geometrically. Efficiently handling long sequences has always been one of the challenges for large language models.

Previous methods often focused on enabling large language models to adapt to longer sequences during the inference phase. For instance, using Alibi or similar relative position encoding methods to allow the model to adapt to different input sequence lengths, or employing interpolation on relative position encodings like RoPE to conduct further fine-tuning on already trained models to achieve the goal of extending sequence lengths. These methods only endow large models with a certain capability for long sequence modeling, but the actual training and inference costs remain unchanged.

The OpenNLPLab team attempts to solve the long sequence problem for large language models once and for all. They proposed and open-sourced Lightning Attention-2—a new linear attention mechanism that aligns the training and inference costs of long sequences with those of a 1K sequence length. Before hitting the memory bottleneck, infinitely increasing the sequence length does not negatively impact the model training speed. This makes infinite-length pre-training possible. Meanwhile, the inference cost for ultra-long texts is consistent with or even less than that of 1K tokens, which greatly reduces the current inference costs of large language models. As shown in the figure below, at model sizes of 400M, 1B, and 3B, as the sequence length increases, the training speed of LLaMA with FlashAttention2 starts to decline rapidly, while the speed of TansNormerLLM with Lightning Attention-2 remains virtually unchanged.

Figure 1

• Paper: Lightning Attention-2: A Free Lunch for Handling Unlimited Sequence Lengths in Large Language Models
• Paper Link: https://arxiv.org/pdf/2401.04658.pdf
• Open Source Link: https://github.com/OpenNLPLab/lightning-attention

Overview of Lightning Attention-2

Maintaining consistent pre-training speed for large models across different sequence lengths sounds like an impossible task. In fact, if the computational complexity of an attention mechanism remains linear with respect to sequence length, this can be achieved. Since the advent of linear attention in 2020, researchers have been striving to ensure that the practical efficiency of linear attention aligns with its theoretical linear computational complexity. Before 2023, most works on linear attention focused on aligning their accuracy with that of Transformers. Finally, in mid-2023, improved linear attention mechanisms achieved accuracy comparable to state-of-the-art Transformer architectures. However, the most critical computational trick of linear attention that transforms computational complexity into linearity, known as “left multiplication becomes right multiplication,” is far slower in practical implementation than direct left multiplication algorithms. This is due to the right multiplication implementation requiring cumulative summation (cumsum) involving numerous loop operations, resulting in significantly lower efficiency compared to left multiplication due to extensive I/O operations.

Figure 2

To better understand the concept of Lightning Attention-2, let’s first review the computation formula of traditional softmax attention: O=softmax((QK^T)⊙M_) V, where Q, K, V, M, O represent the query, key, value, mask, and output matrix, respectively. Here, M is a lower triangular matrix of ones in unidirectional tasks (like GPT) and can be ignored in bidirectional tasks (like BERT), meaning there is no mask matrix in bidirectional tasks.

The author summarizes the overall concept of Lightning Attention-2 into the following three points for explanation:

1. One of the core ideas of Linear Attention is to eliminate the computationally expensive softmax operator, allowing the attention computation formula to be written as O=((QK^T)⊙M_) V. However, due to the presence of the mask matrix M in unidirectional tasks, this form can still only perform left multiplication, thus not achieving O(N) complexity. For bidirectional tasks, since there is no mask matrix, the computation formula of Linear Attention can be further simplified to O=(QK^T) V. The brilliance of Linear Attention lies in the fact that by merely utilizing the associative property of simple matrix multiplication, its computation formula can be further transformed into: O=Q(K^T V), which is known as right multiplication; the former corresponds to left multiplication. As illustrated in Figure 2, Linear Attention can achieve an enticing O(N) complexity in bidirectional tasks!

2. However, as the decoder-only GPT format model gradually becomes the de facto standard for LLMs, how to leverage the right multiplication property of Linear Attention to accelerate unidirectional tasks has become an urgent problem to solve. To address this issue, the authors propose using a “divide and conquer” approach, partitioning the attention matrix computation into diagonal and non-diagonal forms and employing different methods for their computation. As shown in Figure 3, Linear Attention-2 utilizes the common Tiling concept in computer science, dividing the Q, K, V matrices into an equal number of blocks. The computation within a block (intra-block) retains the left multiplication method due to the presence of the mask matrix, maintaining O(N^2) complexity; while the computation between blocks (inter-block) can utilize the right multiplication method due to the absence of the mask matrix, thereby achieving O(N) complexity. After completing the calculations for both, the corresponding output Oi of Linear Attention for the i-th block can be directly obtained by summing them up. Moreover, by using cumsum to accumulate the KV state for use in the next block’s computation, the overall algorithm complexity of Lightning Attention-2 is thus a trade-off between intra-block O(N^2) and inter-block O(N). How to achieve a better trade-off is determined by the Tiling block size.

3. Observant readers will note that the above process only covers the algorithm portion of Lightning Attention-2. It is named Lightning because the authors fully consider the efficiency of this algorithm during GPU hardware execution. Inspired by the FlashAttention series of works, during actual computation on the GPU, the authors transport the split Q_i, K_i, V_i tensors from the slower, larger HBM to the faster, smaller SRAM for computation, thus significantly reducing memory I/O overhead. After the block completes the Linear Attention computation, its output O_i is transported back to HBM. This process is repeated until all blocks are processed.

Readers interested in more details can carefully read Algorithm 1 and Algorithm 2 in this article, as well as the detailed derivation process in the paper. The algorithms and derivation process distinguish between the forward and backward processes of Lightning Attention-2, helping readers gain a deeper understanding.

Figure 3

Accuracy Comparison of Lightning Attention-2

The researchers first compared the accuracy differences between Lightning Attention-2 and Lightning Attention-1 on a small-scale (400M) parameter model, as shown in the figure below, with negligible differences between the two.

Subsequently, researchers compared the TransNormerLLM (TNL-LA2) powered by Lightning Attention-2 with other advanced non-Transformer architectures and LLaMA powered by FlashAttention2 under the same corpus on 1B and 3B. As shown in the figure below, TNL-LA2 maintained a similar trend with LLaMA and exhibited superior loss performance. This experiment demonstrates that Lightning Attention-2 achieves accuracy performance comparable to that of state-of-the-art Transformer architectures in language modeling.

In large language model tasks, researchers compared the TNL-LA2 15B with Pythia on common benchmarks for large models of similar sizes. As shown in the table below, under the condition of consuming the same tokens, TNL-LA2 outperformed the Pythia model based on softmax attention in terms of commonsense reasoning and multiple-choice comprehensive abilities.

Speed Comparison of Lightning Attention-2

The researchers compared the single-module speed and memory usage of Lightning Attention-2 with FlashAttention2. As shown in the figure below, compared to Lightning Attention-1 and FlashAttention2, Lightning Attention-2 exhibits a strictly linear growth in speed concerning sequence length. In terms of memory usage, all three show a similar trend, but Lightning Attention-2 has lower memory usage. This is because the memory usage of FlashAttention2 and Lightning Attention-1 is also approximately linear.

The author notes that this article primarily focuses on addressing the training speed of linear attention networks and achieving training speeds for arbitrary-length long sequences similar to those of 1K sequences. There is not much introduction regarding inference speed. This is because linear attention can be losslessly transformed into RNN mode during inference, thus achieving a similar effect, meaning that the inference speed of a single token is constant. For Transformers, the current token’s inference speed is related to the number of previous tokens.

The author tested the inference speed comparison between TransNormerLLM-7B powered by Lightning Attention-1 and common 7B models. As shown in the figure below, at approximately similar parameter sizes, the throughput speed of Lightning Attention-1 is four times that of Baichuan and more than 3.5 times that of ChatGLM, demonstrating excellent advantages in inference speed.

Conclusion

Lightning Attention-2 represents a significant advancement in linear attention mechanisms, enabling it to perfectly replace traditional softmax attention in terms of both accuracy and speed, providing sustainable scalability for increasingly larger models and offering a pathway to efficiently handle infinitely long sequences. The OpenNLPLab team will explore sequence parallel algorithms based on linear attention mechanisms in the future to address the current memory barrier issues.

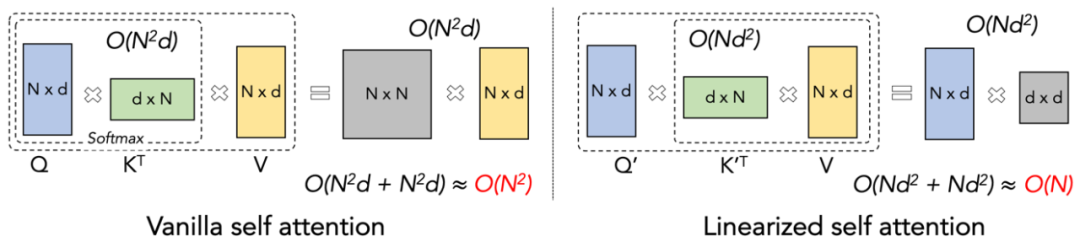
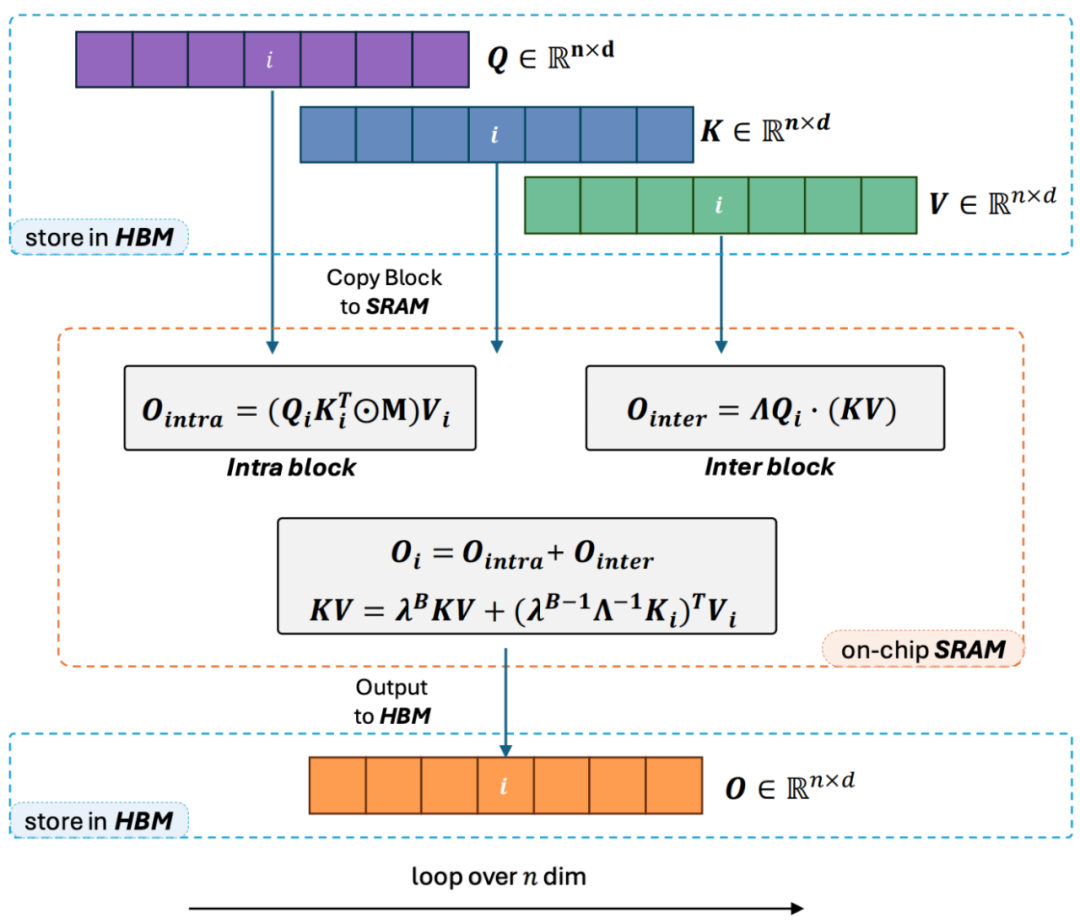
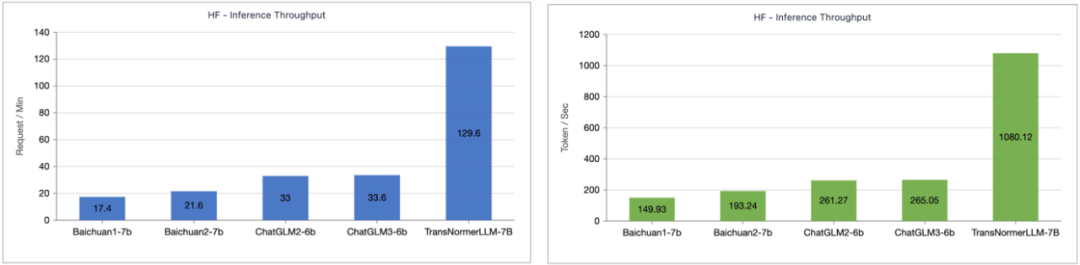
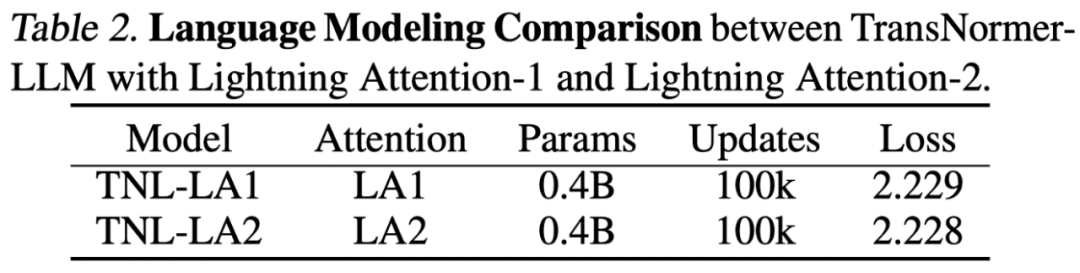
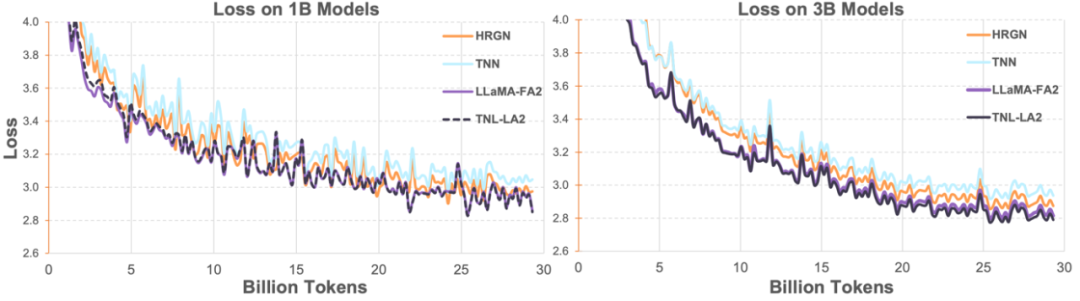
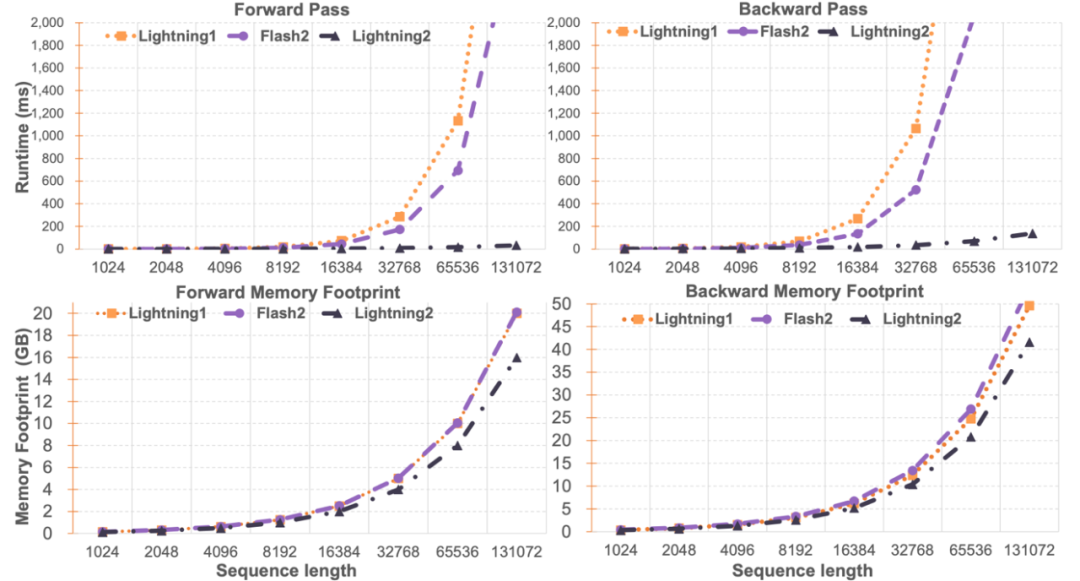
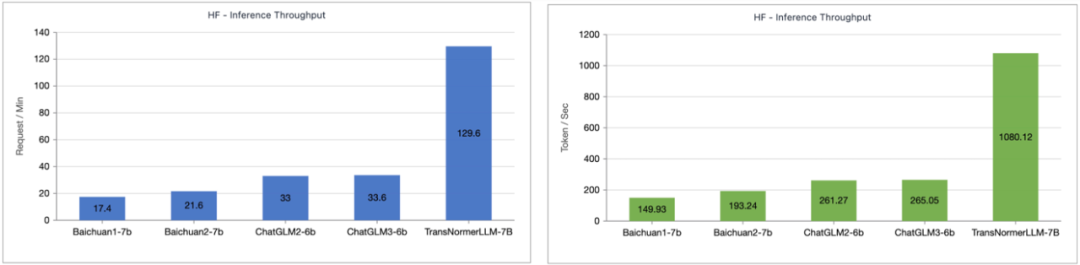
Source: Machine Heart

More AI and Human-Computer Interaction

Welcome to join the discussion group

Scan to add assistant WeChat

Note: “Add XR group,” to join the discussion group

For academic exchange only, if infringement, please leave a message, immediate deletion!

Your every view is very important to me