Skip to content
Reprinted from: Machine Heart
Lightning Attention-2 is a new type of linear attention mechanism that aligns the training and inference costs of long sequences with those of a 1K sequence length.
The limitation of sequence length in large language models greatly restricts their applications in the field of artificial intelligence, such as multi-turn dialogue, long text understanding, and multimodal data processing and generation. The fundamental reason for this limitation lies in the quadratic computational complexity relative to sequence length inherent in the Transformer architecture currently adopted by all large language models. This means that as the sequence length increases, the required computational resources increase geometrically. Efficiently handling long sequences has always been one of the challenges for large language models.
Previous methods often focused on how to adapt large language models to longer sequences during the inference stage. For instance, using Alibi or similar relative position encoding methods to allow the model to adapt to different input sequence lengths, or employing interpolation methods on relative position encodings like RoPE to further fine-tune already trained models to achieve the goal of extending sequence lengths. These methods merely endow large models with a certain capability for modeling long sequences, but the actual training and inference overhead has not decreased.
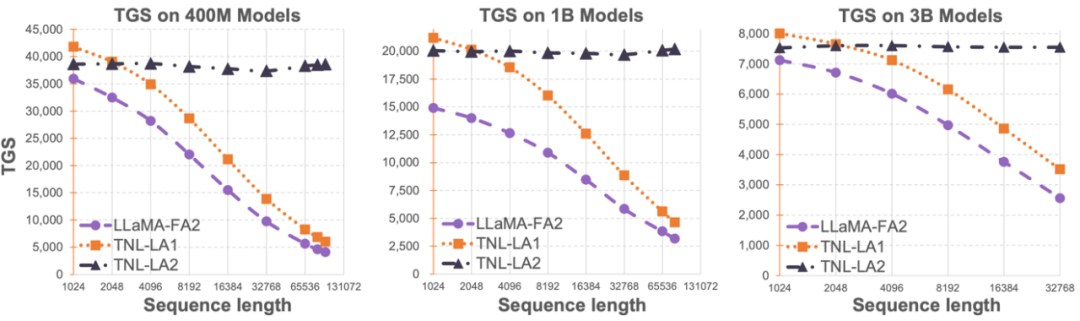
The OpenNLPLab team attempted to solve the long sequence problem of large language models once and for all. They proposed and open-sourced Lightning Attention-2—a new type of linear attention mechanism that aligns the training and inference costs of long sequences with those of a 1K sequence length. Before encountering GPU memory bottlenecks, infinitely increasing sequence lengths does not negatively impact the model training speed. This makes unlimited-length pre-training possible. At the same time, the inference cost for ultra-long texts is consistent with that of 1K tokens or even lower, which will greatly reduce the current inference costs of large language models. As shown in the figure below, with model sizes of 400M, 1B, and 3B, as the sequence length increases, the training speed of LLaMA enhanced by FlashAttention2 begins to decline rapidly, whereas the speed of TansNormerLLM enhanced by Lightning Attention-2 remains virtually unchanged.

-
Paper: Lightning Attention-2: A Free Lunch for Handling Unlimited Sequence Lengths in Large Language Models
-
Paper link: https://arxiv.org/pdf/2401.04658
-
Open-source link: https://github.com/OpenNLPLab/lightning-attention
Introduction to Lightning Attention-2
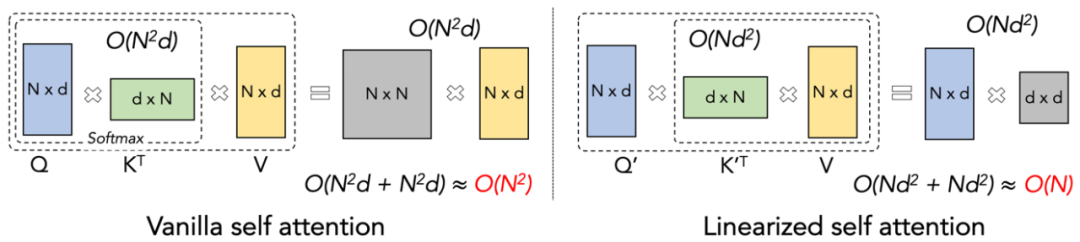
Maintaining consistent pre-training speed of large models across different sequence lengths sounds like an impossible task. In fact, if an attention mechanism’s computational complexity maintains a linear relationship relative to sequence length, this can be achieved. Since the advent of linear attention in 2020, researchers have been working hard to ensure the practical efficiency of linear attention aligns with its theoretical linear computational complexity. Before 2023, most of the work on linear attention focused on aligning their accuracy with that of Transformers. Finally, in mid-2023, improved linear attention mechanisms achieved accuracy comparable to state-of-the-art Transformer architectures. However, the key computational trick of “left multiplication becoming right multiplication” to make the computational complexity linear in linear attention is far slower in practical implementation than direct left multiplication algorithms. This is due to the right multiplication implementation requiring cumulative summation (cumsum) involving a large number of loop operations, which makes the efficiency of right multiplication much lower than that of left multiplication.
 To better understand the ideas behind Lightning Attention-2, let us first review the computational formula of traditional softmax attention: O=softmax ((QK^T)⊙M_) V, where Q, K, V, M, O represent the query, key, value, mask, and output matrix, respectively. Here, M is a lower triangular matrix of all 1s in unidirectional tasks (like GPT) and can be ignored in bidirectional tasks (like BERT), meaning bidirectional tasks do not have a mask matrix.
The author summarizes the overall ideas of Lightning Attention-2 into three points for explanation:
1. One of the core ideas of Linear Attention is to eliminate the computationally expensive softmax operator, allowing the attention computation formula to be written as O=((QK^T)⊙M_) V. However, due to the presence of the mask matrix M in unidirectional tasks, this form can still only perform left multiplication, thus failing to achieve O (N) complexity. But for bidirectional tasks, since there is no mask matrix, the computation formula of Linear Attention can be further simplified to O=(QK^T) V. The brilliance of Linear Attention lies in its ability to further transform its computation formula using the simple associative property of matrix multiplication: O=Q (K^T V), which is known as right multiplication, while the former is left multiplication. As illustrated in Figure 2, Linear Attention can achieve an enticing O (N) complexity in bidirectional tasks!
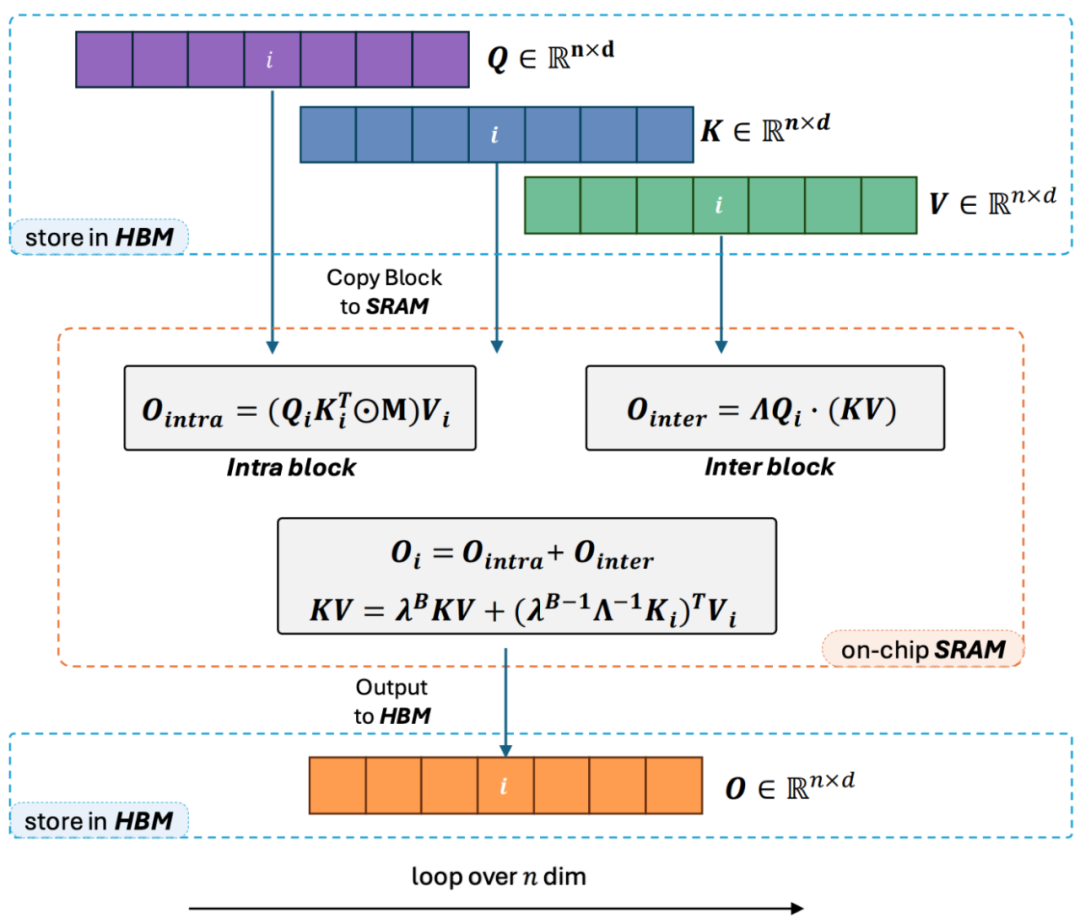
2. However, as the decoder-only GPT form of model gradually becomes the de facto standard for LLMs, how to leverage the right multiplication feature of Linear Attention to accelerate unidirectional tasks has become an urgent problem to solve. To address this issue, the authors propose using a “divide and conquer” approach, splitting the attention matrix computation into diagonal and non-diagonal forms, and employing different methods to compute them. As shown in Figure 3, Linear Attention-2 utilizes the common Tiling concept in computer science, dividing the Q, K, V matrices into the same number of blocks. The intra-block computation retains the left multiplication method due to the presence of the mask matrix, maintaining O (N^2) complexity. However, inter-block computation, due to the absence of a mask matrix, can utilize right multiplication, thus enjoying O (N) complexity. After both are computed separately, they can be directly summed to obtain the corresponding Linear Attention output Oi for block i. Meanwhile, the cumsum is used to accumulate the state of KV for use in the computation of the next block. This results in the overall algorithm complexity of Lightning Attention-2 being a trade-off between the intra-block O (N^2) and inter-block O (N). How to achieve a better trade-off is determined by the Tiling block size.
3. Observant readers will notice that the above process only covers the algorithm part of Lightning Attention-2. The reason it is named Lightning is that the authors fully consider the efficiency of this algorithmic process during GPU hardware execution. Inspired by the FlashAttention series of work, when performing computations on the GPU, the authors move the divided Q_i, K_i, V_i tensors from the slower, larger HBM (High Bandwidth Memory) to the faster, smaller SRAM (Static Random Access Memory) for computation, thereby reducing significant memory I/O overhead. Once the block completes the Linear Attention computation, its output O_i is moved back to HBM. This process is repeated until all blocks are processed.
Readers interested in more details can carefully read Algorithm 1 and Algorithm 2 in this article, as well as the detailed derivation process in the paper. The algorithms and derivation processes distinguish between the forward and backward processes of Lightning Attention-2, helping readers gain a deeper understanding.
To better understand the ideas behind Lightning Attention-2, let us first review the computational formula of traditional softmax attention: O=softmax ((QK^T)⊙M_) V, where Q, K, V, M, O represent the query, key, value, mask, and output matrix, respectively. Here, M is a lower triangular matrix of all 1s in unidirectional tasks (like GPT) and can be ignored in bidirectional tasks (like BERT), meaning bidirectional tasks do not have a mask matrix.
The author summarizes the overall ideas of Lightning Attention-2 into three points for explanation:
1. One of the core ideas of Linear Attention is to eliminate the computationally expensive softmax operator, allowing the attention computation formula to be written as O=((QK^T)⊙M_) V. However, due to the presence of the mask matrix M in unidirectional tasks, this form can still only perform left multiplication, thus failing to achieve O (N) complexity. But for bidirectional tasks, since there is no mask matrix, the computation formula of Linear Attention can be further simplified to O=(QK^T) V. The brilliance of Linear Attention lies in its ability to further transform its computation formula using the simple associative property of matrix multiplication: O=Q (K^T V), which is known as right multiplication, while the former is left multiplication. As illustrated in Figure 2, Linear Attention can achieve an enticing O (N) complexity in bidirectional tasks!
2. However, as the decoder-only GPT form of model gradually becomes the de facto standard for LLMs, how to leverage the right multiplication feature of Linear Attention to accelerate unidirectional tasks has become an urgent problem to solve. To address this issue, the authors propose using a “divide and conquer” approach, splitting the attention matrix computation into diagonal and non-diagonal forms, and employing different methods to compute them. As shown in Figure 3, Linear Attention-2 utilizes the common Tiling concept in computer science, dividing the Q, K, V matrices into the same number of blocks. The intra-block computation retains the left multiplication method due to the presence of the mask matrix, maintaining O (N^2) complexity. However, inter-block computation, due to the absence of a mask matrix, can utilize right multiplication, thus enjoying O (N) complexity. After both are computed separately, they can be directly summed to obtain the corresponding Linear Attention output Oi for block i. Meanwhile, the cumsum is used to accumulate the state of KV for use in the computation of the next block. This results in the overall algorithm complexity of Lightning Attention-2 being a trade-off between the intra-block O (N^2) and inter-block O (N). How to achieve a better trade-off is determined by the Tiling block size.
3. Observant readers will notice that the above process only covers the algorithm part of Lightning Attention-2. The reason it is named Lightning is that the authors fully consider the efficiency of this algorithmic process during GPU hardware execution. Inspired by the FlashAttention series of work, when performing computations on the GPU, the authors move the divided Q_i, K_i, V_i tensors from the slower, larger HBM (High Bandwidth Memory) to the faster, smaller SRAM (Static Random Access Memory) for computation, thereby reducing significant memory I/O overhead. Once the block completes the Linear Attention computation, its output O_i is moved back to HBM. This process is repeated until all blocks are processed.
Readers interested in more details can carefully read Algorithm 1 and Algorithm 2 in this article, as well as the detailed derivation process in the paper. The algorithms and derivation processes distinguish between the forward and backward processes of Lightning Attention-2, helping readers gain a deeper understanding.

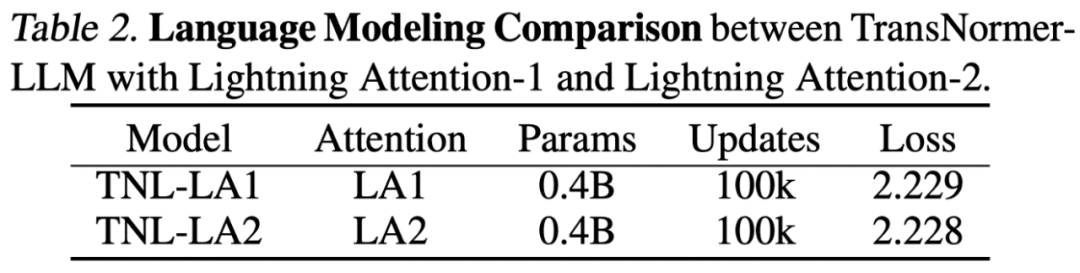
Accuracy Comparison of Lightning Attention-2
The researchers first compared the accuracy differences between Lightning Attention-2 and Lightning Attention-1 on a small-scale (400M) parameter model, as shown in the figure below, where both are nearly indistinguishable.
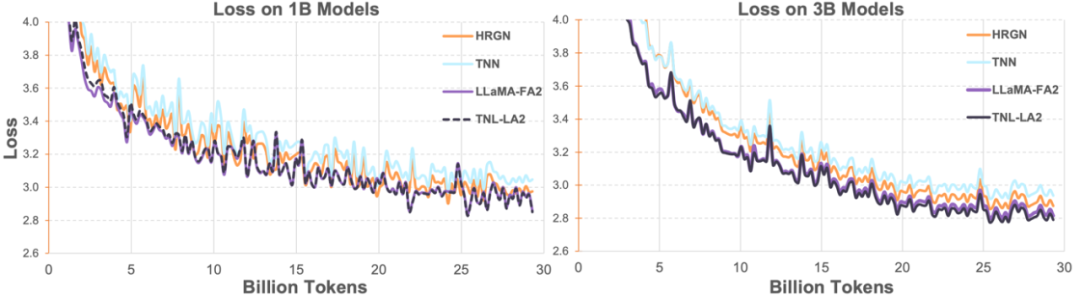
Subsequently, the researchers compared the TransNormerLLM (TNL-LA2) enhanced by Lightning Attention-2 with other advanced non-Transformer architectures and LLaMA enhanced by FlashAttention2 under the same corpus conditions at 1B and 3B. As shown in the figure below, TNL-LA2 maintained a similar trend to LLaMA, with better loss performance. This experiment indicates that Lightning Attention-2 exhibits accuracy performance in language modeling comparable to that of state-of-the-art Transformer architectures.
In large language model tasks, the researchers compared TNL-LA2 15B with the Pythia model at a similar size on common benchmarks. As shown in the table below, under the condition of consuming the same tokens, TNL-LA2 slightly outperformed the Pythia model based on Softmax attention in common sense reasoning and multiple-choice comprehensive abilities.

Speed Comparison of Lightning Attention-2
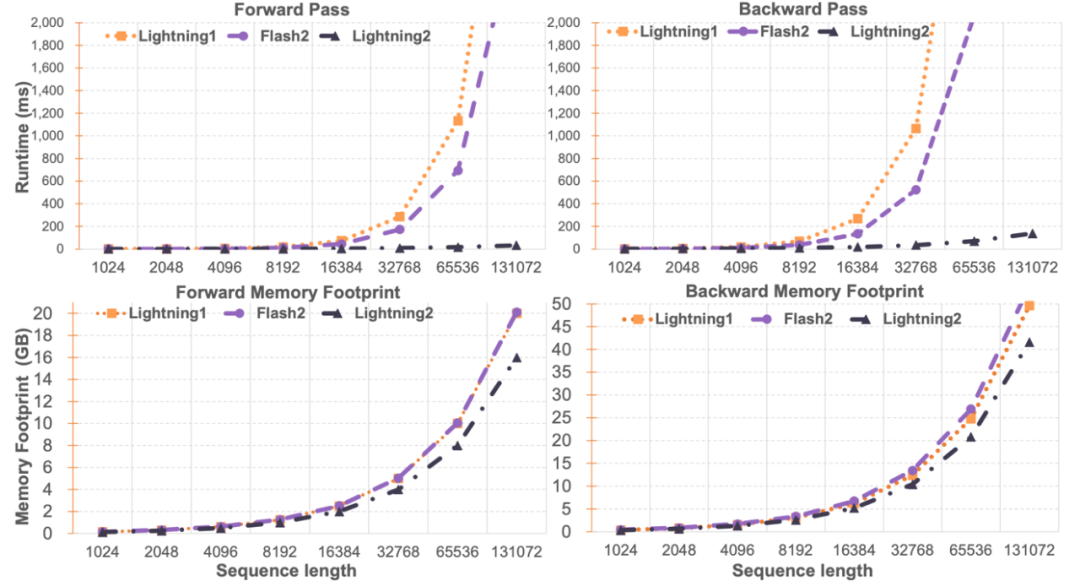
The researchers compared the single-module speed and memory usage of Lightning Attention-2 with FlashAttention2. As shown in the figure below, compared to Lightning Attention-1 and FlashAttention2, Lightning Attention-2 exhibited a strictly linear increase in speed relative to sequence length. In terms of memory usage, all three showed similar trends, but Lightning Attention-2 had lower memory usage. This is because the memory usage of FlashAttention2 and Lightning Attention-1 is also approximately linear.
The author notes that this article mainly focuses on solving the training speed of linear attention networks and achieving a training speed for arbitrary-length long sequences similar to that of 1K sequences. There is not much introduction regarding inference speed. This is because linear attention can be losslessly transformed into RNN mode during inference, thereby achieving a similar effect, i.e., the inference speed of a single token remains constant. For Transformers, the current token’s inference speed is related to the number of previous tokens.
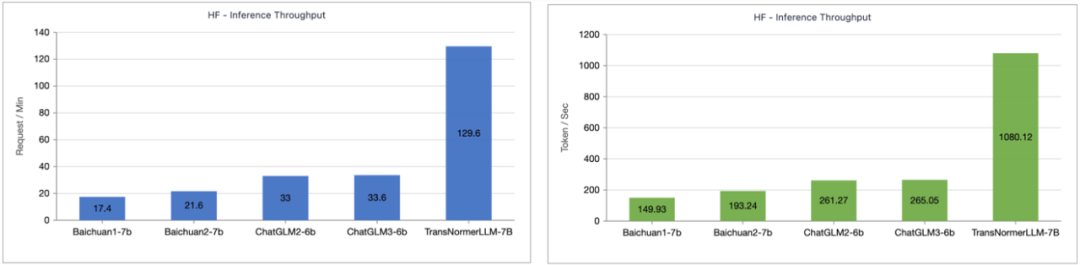
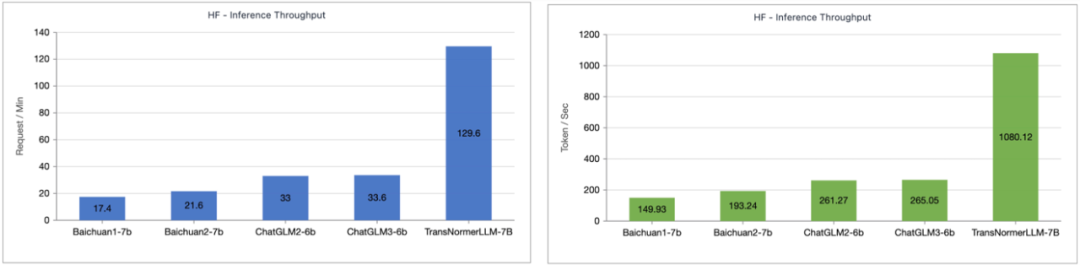
The author tested the inference speed comparison between TransNormerLLM-7B enhanced by Lightning Attention-1 and common 7B models. As shown in the figure below, at approximately the same parameter size, the throughput speed of Lightning Attention-1 is 4 times that of Baichuan and more than 3.5 times that of ChatGLM, demonstrating excellent advantages in inference speed.
Lightning Attention-2 represents a significant advancement in linear attention mechanisms, allowing it to perfectly replace traditional Softmax attention in terms of both accuracy and speed, providing sustainable scalability for increasingly larger models and offering a pathway to efficiently handle infinitely long sequences. The OpenNLPLab team will research sequence parallel algorithms based on linear attention mechanisms in the future to address the current memory bottleneck issues.