In April this year, Max Tegmark’s team released a brand new deep learning network structure called the Kolmogorov-Arnold Network (KAN), which quickly caused a sensation. First author Liu Ziming detailed the team’s latest work at the AI+Science reading club of the Jizhi Club (See: Liu Ziming’s Live Summary: The Capability Boundaries and Outstanding Problems of KAN). In August, they again released the extension work, KAN 2.0, which not only presents an optimized and upgraded network architecture but also a research paradigm of AI+Science. This paradigm makes AI+Science research more interactive and interpretable, hoping to support the development of “curiosity-driven science.” The well-known popular science magazine Quanta Magazine recently reviewed and organized the research process of the KAN series of works. This article is a translation of that article.
Research Fields: AI+Science, Deep Learning, Neural Networks, AI Interpretability
Steve Nadis | Author
Liu Ziming | Translator
“Neural networks are currently the most powerful tools in artificial intelligence. When applied to larger datasets, nothing can compete with them,” said Sebastian Wetzel, a researcher at the Perimeter Institute for Theoretical Physics.
However, for a long time, neural networks have had a drawback: the basic building block known as the multilayer perceptron (MLP) is the foundation of many successful neural networks, yet humans currently cannot understand how networks based on these MLPs arrive at results, or whether there is some underlying principle to explain those results. The astonishing feats performed by neural networks are hidden behind a “black box,” much like a magician’s performance. AI researchers have long pondered whether there could be a different type of network that provides equally reliable results in a more transparent manner.
A study in April 2024 proposed an alternative neural network design called the Kolmogorov-Arnold Network (KAN), which is more transparent and can accomplish nearly all the work of conventional neural networks in certain categories of problems. It is based on a mathematical concept from the mid-20th century that has been rediscovered and reconfigured for applications in the deep learning era.
Despite this innovation being only a few months old, the new design has already sparked widespread interest in both the research and programming communities. “KANs are easier to explain and may be particularly suitable for scientific applications, where they can extract scientific rules from data,” said Alan Yuille, a computer scientist at Johns Hopkins University. “They are an exciting new alternative to widely used MLPs.” Researchers have begun to learn how to maximize their new capabilities.
Paper Title: KAN: Kolmogorov-Arnold Networks
Paper Link: https://arxiv.org/abs/2404.19756
Related Tweet: Liu Ziming’s Live Summary: The Capability Boundaries and Outstanding Problems of KAN
>> At the AI+Science reading club, Liu Ziming detailed the latest work of Max Tegmark’s team. Friends interested are welcome to scan the code to watch the video replay:
KAN: Fitting the “Impossible”
A typical neural network works like this: multiple layers of artificial neurons (nodes) are interconnected through artificial synapses (or edges). Information is processed through each layer and passed to the next layer until the final output. Edges are assigned different weights, with those having larger weights having a greater influence than others. During training, these weights are continuously adjusted so that the network’s output gets closer to the correct answer.
A common goal of neural networks is to find the mathematical function or curve that best connects certain data points. The closer the network is to that function, the better its predictions and the more accurate the results. If your neural network simulates a physical process, the output function ideally represents an equation describing that physical process—equivalent to a physical law.
For MLPs, there is a mathematical theorem that tells us how close the network can get to the optimal function. One of its conclusions is that MLPs cannot perfectly represent that function. But under appropriate conditions, KAN can.
KAN fundamentally differs from MLPs in how it fits functions (connecting the points of network output). KAN does not rely on edges with numerical weights, but instead uses functions. These edge functions are non-linear and can represent more complex curves. They are also learnable, allowing for more sensitive adjustments than the simple numerical weights of MLPs.
However, for the past 35 years, KAN has been considered impractical. In 1989, a paper co-authored by MIT physicist turned computational neuroscientist Tomaso Poggio explicitly stated that the mathematical ideas at KAN’s core were “irrelevant in the context of network learning.” One of Poggio’s concerns can be traced back to KAN’s core mathematical concepts. In 1957, mathematicians Andrey Kolmogorov and Vladimir Arnold demonstrated in their papers that if you have a mathematical function using multiple variables, you can transform it into a combination of multiple functions, each containing only one variable.
Kolmogorov’s paper on the theorem: https://cs.uwaterloo.ca/~y328yu/classics/Kolmogorov57.pdf
Arnold’s paper on the same subject: https://link.springer.com/chapter/10.1007/978-3-642-01742-1_2
However, there is an important limitation. The single-variable functions generated by the theorem may not be “smooth” and could have sharp edges like V-shaped vertices. This poses a problem for any network attempting to use the theorem to reconstruct multi-variable functions. These simpler single-variable parts need to be smooth in order to correctly bend during training to match the target values.
Andrey Kolmogorov (left image) and Vladimir Arnold proved in 1957 that a complex mathematical function can be rewritten as a combination of simpler functions.
So KANs seemed bleak—until one cold day in January this year, MIT physics graduate Liu Ziming decided to revisit the topic. He and his advisor, MIT physicist Max Tegmark, had been exploring how to make neural networks more understandable in scientific applications—hoping to peek inside the black box—but progress was slow. Out of frustration, Liu Ziming decided to study the Kolmogorov-Arnold theorem. “Why not give it a try and see how it works, even though people haven’t paid much attention to it in the past?”
Liu Ziming used the Kolmogorov-Arnold theorem to construct a new neural network.
Tegmark, familiar with Poggio’s paper, thought this attempt would hit a dead end again. But Liu Ziming did not get discouraged, and Tegmark quickly changed his mind. They realized that even if the single-variable functions generated by the theorem were not smooth, the network could still approximate them with smooth functions. They further understood that most of the functions we encounter in science are smooth, making perfect (rather than approximate) representation potentially achievable.
Liu Ziming did not want to give up on this idea without trying, as he knew that since Poggio’s paper was published 35 years ago, software and hardware had made tremendous progress. From a computational perspective, many things in 2024 are unimaginable compared to 1989.
Liu Ziming worked on this idea for about a week, during which he developed several prototype KAN systems, all of which had only two layers—this is the simplest network, and the type that researchers have focused on for decades. The two-layer KAN seemed like the obvious choice, as the Kolmogorov-Arnold theorem essentially provides a blueprint for this structure. The theorem specifically decomposes multi-variable functions into different sets of internal and external functions. (These functions replace the activation functions of edges with weights in MLPs.) This arrangement naturally fits the KAN structure with inner and outer neurons—a common arrangement in simple neural networks.However, to Liu Ziming’s frustration, his prototypes did not perform as well as envisioned in science-related tasks. Tegmark then proposed a crucial suggestion: why not try a KAN with more than two layers, which might handle more complex tasks?

Liu Ziming’s advisor, Max Tegmark, proposed the key suggestion to make the Kolmogorov-Arnold network work successfully: why not build a KAN with more than two layers?
This out-of-the-box idea was the breakthrough they needed. Liu Ziming’s new network architecture began to show potential, and the two quickly reached out to colleagues at MIT, Caltech, and Northeastern University. They hoped to have mathematicians on the team, as well as experts in the fields they planned to analyze using KAN.
In the April paper, the team demonstrated that a three-layer KAN is indeed feasible and provided an example of how a three-layer KAN can accurately represent a certain function (which a two-layer KAN cannot). They did not stop there. The team subsequently conducted experiments with up to six layers, and with each additional layer, the network could align with more complex output functions. “We found that we could basically stack layers arbitrarily,” said Yixuan Wang, one of the paper’s co-authors.
Experimental Validation from Mathematics and Condensed Matter Physics
The researchers also applied their networks to two real-world problems. The first problem involves a mathematical branch called knot theory (knot theory). In 2021, a team from DeepMind announced that they had built an MLP capable of predicting a certain topological property of a given knot after inputting enough other attributes of the knot. Three years later, the new KAN replicated this feat. It then went further to show how the predicted property is associated with all other attributes—Liu Ziming stated this is something “that MLPs are completely incapable of.”
The second problem concerns a phenomenon in condensed matter physics known as Anderson localization (Anderson localization). The goal is to predict the boundary at which a specific phase transition occurs and then determine the mathematical formula describing that process. No MLPs were capable of achieving this, while KAN succeeded.
But the greatest advantage of KAN over other forms of neural networks, and the primary motivation for its recent progress, lies in its interpretability, Tegmark explained. In both examples, KAN not only provided answers but also explanations. “What do we mean by interpretability?” he asked. “If you give me some data, I will give you a formula that can be written on a T-shirt.”
Johns Hopkins University physicist Brice Ménard said that although KAN’s capabilities are currently limited, they suggest that these networks could theoretically teach us something new about the world. “If a problem can actually be described by a simple equation, KAN networks are very good at finding it,” he said. But he warned that KAN’s best-suited domains may be limited to problems in physics—where the equations typically have few variables.
Liu Ziming and Tegmark agree with this point, but do not see it as a drawback. “Almost all famous scientific formulas—like E=mc²—can be expressed as functions of one or two variables,” Tegmark said. “Most of the calculations we do rely on one or two variables. KAN takes advantage of this fact and searches for solutions in this form.”
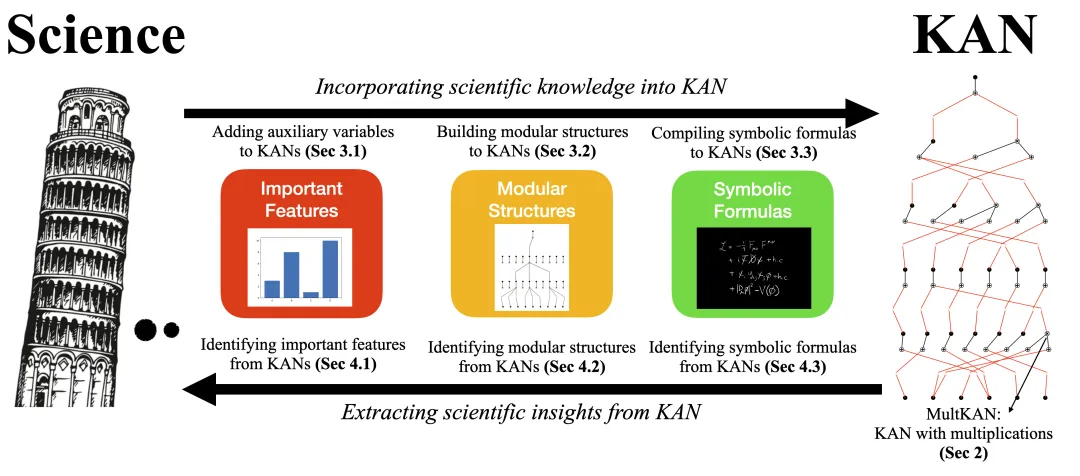
KAN 2.0: Promoting Curiosity-Driven Science
Liu Ziming and Tegmark’s KAN paper quickly caused a sensation, receiving 75 citations within about three months. Soon after, other research groups began to develop their own KANs. A paper authored by Wang Yizheng and others from Tsinghua University went online in June, showing that their Kolmogorov-Arnold Inspired Neural Network (Kolmogorov-Arnold-informed neural network, KINN) “significantly outperforms MLPs in solving partial differential equations (PDEs).”
Paper Title: Kolmogorov Arnold Informed Neural Network: A Physics-informed Deep Learning Framework for Solving Forward and Inverse Problems Based on Kolmogorov Arnold Networks
Paper Link: https://arxiv.org/abs/2406.11045
Researchers at the National University of Singapore published a more complex conclusion in July. They found that KAN performs better than MLPs on tasks related to interpretability, while MLPs perform better in computer vision and audio processing. The two are roughly equal on natural language processing and other machine learning tasks. For Liu Ziming, these results were not surprising, as the initial focus of the KAN team had always been on “science-related tasks,” where interpretability is a top priority.
Paper Title: KAN or MLP: A Fairer Comparison
Paper Link: https://arxiv.org/abs/2407.16674
Meanwhile, Liu Ziming is working to make KAN more practical and user-friendly. In August, he and his collaborators published a new paper called “KAN 2.0,” which he described as “more like a user manual than a traditional paper.” Liu Ziming stated that this version is easier for users and provides features such as multiplication tools that were lacking in the original model.
Paper Title: KAN 2.0: Kolmogorov-Arnold Networks Meet Science
Paper Link: https://arxiv.org/abs/2408.10205
Related Tweet: KAN 2.0 Shocking Release: Building a New Paradigm of AI+Science Unification
He and his co-authors believe that this type of network is not just a means to an end. KANs facilitate what the team calls “curiosity-driven science,” which complements the “application-driven science” that has long dominated machine learning. For example, when observing celestial motion, application-driven researchers focus on predicting their future states, while curiosity-driven researchers seek to uncover the physical principles behind the motion. Liu Ziming hopes that through KANs, researchers can gain more from neural networks, not just help solve difficult computational problems. They can focus on studying purely for understanding.
This article is translated from Quanta Magazine, original link:
https://www.quantamagazine.org/novel-architecture-makes-neural-networks-more-understandable-20240911/
AI+Science is a trend that has emerged in recent years, combining artificial intelligence and science. On one hand, AI for Science, machine learning and other AI technologies can be used to solve problems in scientific research, from predicting weather and protein structures to simulating galaxy collisions, optimizing nuclear fusion reactors, and even making scientific discoveries like a scientist, known as the “fifth paradigm” of scientific discovery. On the other hand, Science for AI, scientific principles and ideas, especially those in physics, inspire machine learning theories, providing new perspectives and methods for the development of artificial intelligence.
The Jizhi Club, together with postdoctoral researcher Wu Tailin from Stanford University’s Computer Science Department (under Professor Jure Leskovec), Harvard Quantum Initiative researcher He Hongye, and MIT physics graduate Liu Ziming (under Professor Max Tegmark), jointly launched a reading club themed on “AI+Science” to explore important issues in this field and study relevant literature together. The reading club has concluded, but you can join the community and unlock replay video access by registering now.

A New Paradigm of Mutual Empowerment between Artificial Intelligence and Scientific Discovery: Launch of the AI+Science Reading Club
1. Liu Ziming’s Live Summary: The Capability Boundaries and Outstanding Problems of KAN
2. KAN 2.0 Shocking Release: Building a New Paradigm of AI+Science Unification
3. Unintentional Willow: Soviet Mathematician Kolmogorov and the Rebirth of Neural Networks
4. Zhang Jiang: The Foundation of Third Generation Artificial Intelligence Technology—From Differentiable Programming to Causal Reasoning | New Course from Jizhi Academy
5.Year of the Dragon: Learning at the Right Time! Unlock All Content from Jizhi and Start a New Year Learning Plan
6. Join Jizhi, let’s get complex!
Click “Read the Original” to Register for the Reading Club