Click on the “Beginner’s Guide to Vision” above, and select “Star” or “Top“
Heavyweight content delivered promptly
Image stitching is a method of merging multiple overlapping images of the same scene into a larger image, which is of great significance in fields such as medical imaging, computer vision, satellite data, and military target automatic recognition. The output of image stitching is the union of two input images. It typically involves five steps:
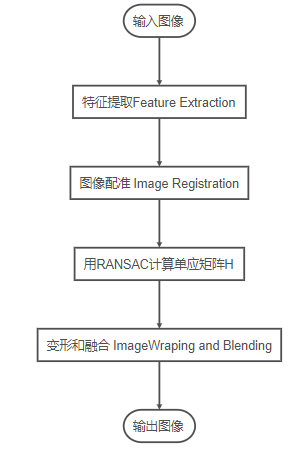
Feature Extraction: Detecting feature points in all input images Image Registration: Establishing the geometric correspondence between images, allowing them to be transformed, compared, and analyzed in a common reference frame. This can be roughly divided into the following categories:
-
Algorithms that directly use pixel values from the images, e.g., correlation methods
-
Algorithms processed in the frequency domain, e.g., FFT-based methods;
-
Low-level feature algorithms, typically using edges and corners, e.g., feature-based methods;
-
High-level feature algorithms, typically using overlapping parts of image objects and feature relationships, e.g., graph-theoretic methods
Image Warping: Image warping refers to the reprojecting of one image and placing it on a larger canvas.
Image Blending: Image blending involves changing the gray levels near the boundaries of the images to remove seams and create a blended image, thereby achieving a smooth transition between the images. Blend modes are used to merge two layers together.
Features are elements in the two input images that need to be matched, which are within blocks of the image. These blocks are groups of pixels in the image. Patch matching is performed on the input images. Specifically, as shown in the figure below, fig1 and fig2 provide a good patch match because a patch in fig2 looks very similar to a patch in fig1. When considering fig3 and fig4, the patches do not match because fig4 contains many similar patches that look like the patch in fig3. Due to the close pixel intensities, precise feature matching cannot be conducted.

To provide better feature matching for image pairs, corner matching is used for quantitative measurements. Corners are good matching features. Corner features are stable under viewpoint changes. Additionally, the neighborhood of a corner has strong intensity changes. Corner detection algorithms are used to detect corners in images. Corner detection algorithms include Harris corner detection, SIFT (Scale Invariant Feature Transform), FAST corner detection, and SURF (Speeded-up Robust Feature) corner detection algorithms.
The Harris algorithm is a point feature extraction algorithm based on the Moravec algorithm. In 1988, C. Harris and M.J. Stephens designed a local detection window for images. By moving the window slightly in different directions, the average change in intensity can be determined. We can easily identify corners by observing the intensity values within a small window.In a flat area, there is no change in intensity in all directions. In edge areas, the intensity does not change along the edge direction. For corner points, significant intensity changes occur in all directions. The Harris corner detector provides a mathematical method for detecting flat areas, edges, and corners. The features detected by Harris have rotation invariance and scale variance.
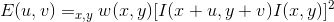 Intensity changes under displacement:
Intensity changes under displacement: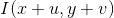 where,
where,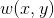 is the window function,
is the window function,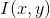 is the intensity after moving, and
is the intensity after moving, and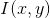 is the intensity of a single pixel location.
is the intensity of a single pixel location.
The Harris corner detection algorithm is as follows:
-
For each pixel in the image
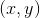 calculate the autocorrelation matrix
calculate the autocorrelation matrix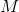 (autocorrelation matrix M):
(autocorrelation matrix M): 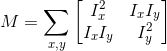 where
where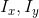 is
is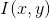 the partial derivative.
the partial derivative. -
Apply Gaussian filtering to each pixel in the image to obtain a new matrix
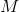 , the discrete two-dimensional zero-mean Gaussian function is
, the discrete two-dimensional zero-mean Gaussian function is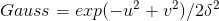
-
Calculate the corner metric for each pixel point (x,y) to obtain
 ,
,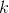 with a range of
with a range of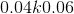 .
. -
Select local maximum points. The Harris method considers that feature points correspond to pixel values at local maxima.
-
Set a threshold T to detect corners. If the local maximum value of
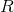 is above the threshold
is above the threshold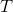 , then this point is a corner.
, then this point is a corner.
The SIFT algorithm is a scale-invariant feature point detection algorithm that can be used to identify similar objects in other images. SIFT’s image features are represented askey-point descriptors. When checking image matches, two sets of key-point descriptors are provided as input toNearest Neighbor Search (NNS), generating a tightly matched key-point descriptor.
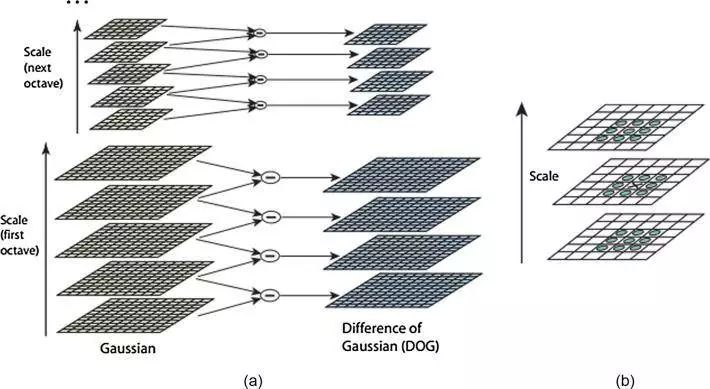 The computation of SIFT is divided into four stages:
The computation of SIFT is divided into four stages:
-
Scale-space construction
-
Scale-space extrema detection
-
Key-point localization
-
Orientation assignment and defining key-point descriptors
The first stage identifies potential interest points. It uses the difference of Gaussian function (DOG) to search across all scales and image locations. The locations and scales of all interest points found in the first stage are determined. Key points are selected based on their stability. A stable key point can resist image distortions. In the orientation assignment stage, the SIFT algorithm calculates the directions of gradients around stable key points. One or more directions are assigned to each key point based on local image gradient directions. For a set of input frames, SIFT extracts features. Image matching uses the Best Bin First (BBF) algorithm to estimate initial matching points between input frames. To remove unwanted corners that do not belong to overlapping areas, the RANSAC algorithm is used. It eliminates incorrect matches in image pairs. The reprojection of frames is achieved by defining the size, length, and width of the frames. Finally, stitching is performed to obtain the final output stitched image. During stitching, each pixel in every frame of the scene is checked to see if it belongs to the distorted second frame. If it does, the value of that pixel is assigned from the corresponding pixel in the first frame. The SIFT algorithm has both rotation invariance and scale invariance. SIFT is well-suited for object detection in high-resolution images. It is a robust image comparison algorithm, although it is slower. The runtime of the SIFT algorithm is significant because comparing two images takes more time.
FAST is a corner detection algorithm created by Trajkovic and Hedley in 1998. For FAST, corner detection is superior to edge detection because corners have two-dimensional intensity variations, making them easy to distinguish from neighboring points. It is suitable for real-time image processing applications.
FAST corner detectors should meet the following requirements:
-
The detected locations should be consistent, insensitive to noise variations, and should not move across multiple images of the same scene.
-
Accuracy; the detected corners should be as close to the correct positions as possible.
-
Speed; the corner detector should be fast enough.
Principle: First, select 16 pixel points around a candidate corner. If n (generally 12) of those pixels are consecutively higher than the candidate corner plus a threshold, or lower than the candidate corner minus a threshold, then this point is considered a corner (as shown in Figure 4).
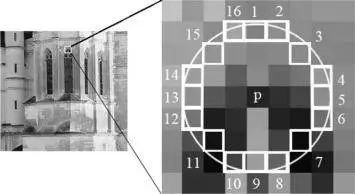
To speed up the FAST algorithm, a corner response function (CRF) is typically used. This function provides a numerical value for corner intensity based on local neighborhood image intensities. The CRF is computed for the image, and the local maxima of the CRF are used as corners, with multi-grid techniques employed to improve the computation speed and suppress false corner detections. FAST is an accurate, fast algorithm with good localization (position accuracy) and high point reliability. The challenge in FAST corner detection lies in selecting the optimal threshold.
Speed-up Robust Feature (SURF) corner detector employs three feature detection steps: Detection, Description, and Matching. SURF accelerates the detection process by considering the quality of detected points, placing more emphasis on speeding up the matching step. It uses the Hessian matrix and low-dimensional descriptors to significantly enhance matching speed. SURF is widely used in the computer vision community and is effective and robust in invariant feature localization.
Once feature points are detected, we need to associate them in some way, which can be done using the NCC or SDD (Sum of Squared Difference) method to determine their correspondence.
The principle of cross-correlation is to analyze the pixel window around each point in the first image and correlate them with the pixel windows around each point in the second image. The points with the highest bidirectional correlation are taken as corresponding pairs.
Based on image intensity values, the similarity between the “windows” of shifts (shifts) in both images is calculated.
 where,
where,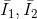 is the mean image of the window
is the mean image of the window
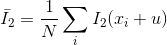
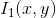 and
and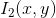 are the two images respectively.
are the two images respectively.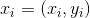 is the pixel coordinate of the window,
is the pixel coordinate of the window,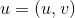 is the displacement or shift calculated by the NCC coefficient. The range of NCC coefficients is
is the displacement or shift calculated by the NCC coefficient. The range of NCC coefficients is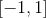 . The displacement parameters corresponding to the peak of NCC represent the geometric transformation between the two images. The advantage of this method is its simplicity in computation, but it is particularly slow. Furthermore, such algorithms require significant overlap between the source images.
. The displacement parameters corresponding to the peak of NCC represent the geometric transformation between the two images. The advantage of this method is its simplicity in computation, but it is particularly slow. Furthermore, such algorithms require significant overlap between the source images.
Mutual information measures the similarity based on the amount of shared information between two images.
Two images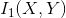 and
and have MI represented in terms of entropy:
have MI represented in terms of entropy:

where,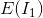 and
and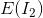 are
are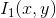 and
and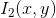 entropies respectively.
entropies respectively.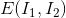 represents the joint entropy between the two images.
represents the joint entropy between the two images.
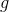 is
is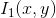 the possible gray values,
the possible gray values,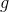 is
is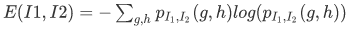 the probability distribution function of
the probability distribution function of .
.
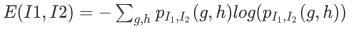
However, as we can see from the image, many points are incorrectly associated.
Homography matrix estimation is the third step in image stitching. In homography matrix estimation, unwanted corners that do not belong to the overlapping area are removed. The RANSAC algorithm is used for homography.
The RANSAC algorithm fits a mathematical model from a dataset that may contain outliers and is an iterative method for robust parameter estimation. The algorithm is uncertain, as it only produces a reasonable result with a certain probability, which increases with more iterations. The RANSAC algorithm is used to fit models robustly in the presence of a large amount of available data. It has many applications in computer vision.
RANSAC Principle
A random subset of data is selected from the dataset and considered valid data (inliers) to determine the parameters of the model to be estimated. This model is then used to test all data in the dataset, and data that satisfies the model becomes inliers, while others are outliers (often noise, erroneous measurements, or incorrect data points). This process is iterated until a parameter model yields the maximum number of inliers, making it the optimal model. The following assumptions are considered:
-
Parameters can be estimated from N data points.
-
The total number of available data points is M.
-
The probability that randomly chosen data points are part of a good model is
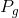 .
. -
If there is a good fit, the probability that the algorithm exits without finding a good fit is
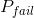 .
.
RANSAC Steps
-
Randomly select N data points (3 point pairs)
-
Estimate parameters x (calculate transformation matrix H)
-
Based on a user-defined threshold, find the total number K of data pairs in M that fit the model vector x (calculate the distance of each matching point after transformation to the corresponding matching point, and classify the matching point set into inliers and outliers based on a pre-defined threshold. If there are enough inliers, then H is reasonable enough, and H is re-estimated using all inliers).
-
If the number of matches K is sufficiently large, accept the model and exit
-
Repeat steps 1-4 L times
-
Exit at this step
The size of K depends on the percentage of data we consider to be part of the suitable structure and how many structures are present in the image. If multiple structures exist, the fitting data will be removed after a successful fit, and RANSAC will be redone.
The number of iterations L can be calculated using the following formula:

Advantages: Can robustly estimate model parameters. Disadvantages: The number of iterations has no upper limit, and the set number of iterations will affect the algorithm’s time complexity and accuracy, and a threshold needs to be preset.
After executing RANSAC, we can only see the correct matches in the image because RANSAC finds a homography matrix associated with most points and discards incorrect matches as outliers.
With two sets of corresponding points, the next step is to establish the transformation relationship between the two sets of points, i.e., the image transformation relationship. Homography is a mapping between two spaces, commonly used to represent the correspondence between two images of the same scene, matching most related feature points and enabling image projection, allowing one image to overlap significantly with another through projection.
Let the matching points of the two images be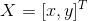 and
and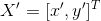 , which must satisfy the formula:
, which must satisfy the formula:
 and since the two vectors are collinear,
and since the two vectors are collinear,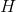 is the 8-parameter transformation matrix, indicating that four points determine one H.
is the 8-parameter transformation matrix, indicating that four points determine one H.
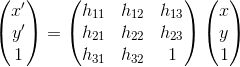
Let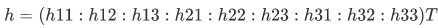 then
then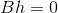 N pairs of points give 2N linear constraints.
N pairs of points give 2N linear constraints.
Estimate H using the RANSAC method:
-
First, detect corner points in both images
-
Apply variance normalized correlation between corner points, collecting pairs with sufficiently high correlation to form a set of candidate matches.
-
Select four points and calculate H
-
Select pairs that are consistent with homography. If for some threshold: Dist(Hp, q) <ε, then the point pair (p, q) is considered consistent with homography H
-
Repeat steps 3 and 4 until enough point pairs satisfy H
-
Using all satisfying point pairs, recalculate H using the formula
The final step is to warp and blend all input images into a conforming output image. Essentially, we can simply warp all input images onto a plane known as the composite panorama plane.
-
First, calculate the warped image coordinate range for each input image to obtain the size of the output image. This can be easily determined by mapping the four corners of each source image and calculating the minimum and maximum values of the coordinates (x,y). Finally, the offsets xoffset and yoffset of the specified reference image origin relative to the output panorama need to be calculated.
-
The next step is to use the backward warping described above to map the pixels of each input image onto the plane defined by the reference image, executing both forward and backward warping of the points.
 Smooth transition (transition smoothing) image blending methods include feathering, pyramid, and gradient.
Smooth transition (transition smoothing) image blending methods include feathering, pyramid, and gradient.
The final step is to blend pixel colors in the overlapping regions to avoid seams. The simplest available form is to use feathering, which uses a weighted average of color values to blend overlapping pixels. We typically use an alpha factor, usually referred to as the alpha channel, which has a value of 1 at the center pixel and linearly decreases to 0 at the boundary pixels. When there are at least two overlapping images in the output stitched image, we will use the following alpha value to calculate the color of a pixel at (x, y): assuming two images , overlapping in the output image; each pixel point
, overlapping in the output image; each pixel point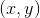 in image
in image , where (R,G,B) are the color values of the pixel, we will calculate the pixel value at (x, y) in the stitched output image:
, where (R,G,B) are the color values of the pixel, we will calculate the pixel value at (x, y) in the stitched output image:
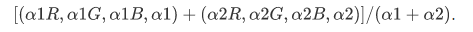


The above content provides a brief overview of some commonly used algorithms. The Harris corner detection method has robustness and rotation invariance. However, it is sensitive to scale changes. The FAST algorithm has rotation invariance and scale invariance, with good execution time. However, its performance is poor in the presence of noise. The SIFT algorithm has both rotation invariance and scale invariance, and is more effective in noisy situations. It has very distinct features. However, it is influenced by lighting changes. This algorithm performs well in execution time and light invariance.
-
The Road to OpenCV (Twenty-Fourth) Image Stitching and Image Fusion Technology
-
Debabrata Ghosh, Naima Kaabouch. A survey on image mosaicing techniques[J]. Journal of Visual Communication and Image Representation, 2016, 34. Address
-
Overview of Image Stitching
Discussion Group
Welcome to join the public account reader group to communicate with peers. Currently, there are WeChat groups on SLAM, three-dimensional vision, sensors, autonomous driving, computational photography, detection, segmentation, recognition, medical imaging, GAN, algorithm competitions, etc. (which will gradually be subdivided in the future). Please scan the WeChat account below to join the group, and note: “Nickname + School/Company + Research Direction”, for example: “Zhang San + Shanghai Jiao Tong University + Vision SLAM”. Please follow the format, otherwise, it will not be approved. After successful addition, you will be invited to join relevant WeChat groups based on research direction. Please do not send advertisements in the group, otherwise you will be removed from the group. Thank you for your understanding~


