Click belowCard, follow the “CVer” public account
AI/CV heavy content delivered instantly
Click to enter—>【Computer Vision and Transformer】Group Chat
Reprinted from: New Intelligence | Edited by:Peach
Click belowCard, follow the “CVer” public account
AI/CV heavy content delivered instantly
Click to enter—>【Computer Vision and Transformer】Group Chat
AI/CV heavy content delivered instantly
Click to enter—>【Computer Vision and Transformer】Group Chat
【Guide】The latest 3D visualization tool “mm” launched by the PyTorch team can simulate the matrix multiplication of the real world.
The simulated world in the matrix is really here.

Matrix multiplication (matmul) is a very important operation in machine learning, especially playing a key role in neural networks.
In a recent article by the PyTorch team, they introduced “mm”, a visualization tool for matmuls and combinations of matmuls.

By using three spatial dimensions, mm can help build intuition and inspire ideas, especially suitable (but not limited to) for visual/spatial thinkers.
NVIDIA senior scientist Jim Fan stated, entering the neural network “matrix”.

This is a very cool visualization tool for matrices, attention, parallelism, etc. The best education comes from the most intuitive delivery. This is a multi-layer perceptron with data parallel segmentation capabilities.

With three dimensions forming matrix multiplication, combined with the ability to load pre-trained weights, you can visualize large composite expressions like attention heads and observe their actual performance with im.
The mm tool is interactive, can run in a browser or notebook iframe, and retains its full state in the URL, sharing dialogue links.
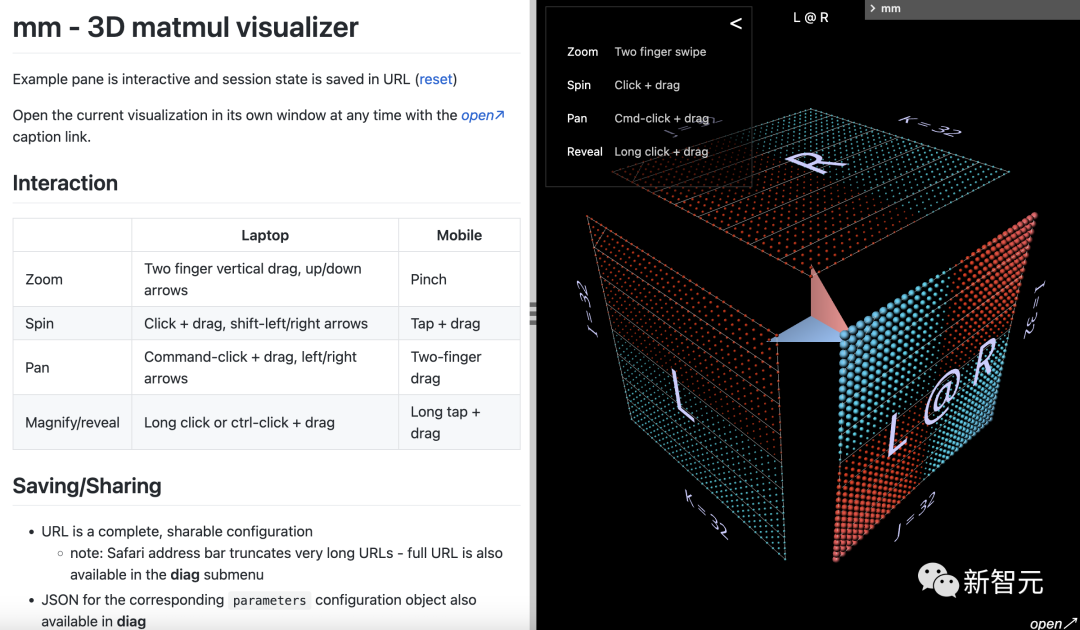
Address: https://bhosmer.github.io/mm/ref.html
In the following, the reference guide provided by PyTorch introduces all available features of mm.
The research team will first introduce visualization methods, building intuition by visualizing some simple matrix multiplications and expressions, and then delve into more examples.
Why is this visualization method better?
The visualization method of mm is based on the premise that matrix multiplication is fundamentally a three-dimensional operation.
In other words:
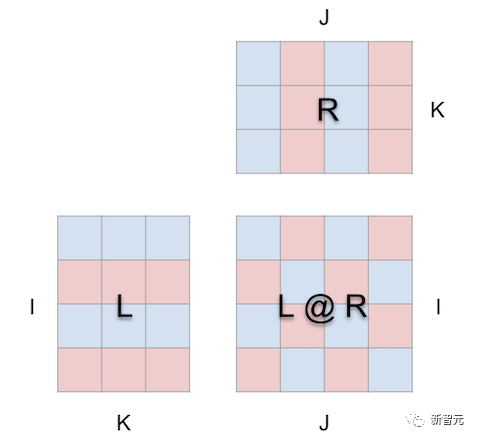
It is a piece of paper, which looks like this after opening with mm:

When we wrap matrix multiplication around a cube in this way, the correct relationships between parameter shapes, result shapes, and shared dimensions are all established.
Now, the calculations have geometric meaning:
Each position i, j in the result matrix anchors a vector running along the depth dimension k inside the cube, where the horizontal plane extending from the i-th row of L and the vertical plane extending from the j-th column of R intersect. Along this vector, the (i, k) (k, j) element pairs from the two parameters meet and multiply, and the resulting products are summed along k, stored in the result at position i, j.
This is the intuitive meaning of matrix multiplication:
– Summing along the third orthogonal dimension to obtain the result matrix
To determine direction, the mm tool displays an arrow pointing to the result matrix inside the cube, with blue indicators coming from the left parameter and red indicators from the right parameter.
The tool also displays white guide lines to indicate the row axes of each matrix, although in this screenshot these guide lines are quite faint.
Of course, the layout constraints are straightforward:
– The left and right parameters must be adjacent along their shared (left width/right height) dimension, which is the depth (k) dimension of matrix multiplication
This geometric representation provides us with a solid foundation for visualizing all standard matrix multiplication decompositions and intuitively exploring the non-trivial combinations of matrix multiplication.
Next, we will see the real matrix world.
Standard matrix multiplication decomposition actions
Before delving into some more complex examples, the PyTorch team will introduce some intuitive builders to understand how things look and feel in this visualization style.
Dot
First is the standard algorithm. Each result element is computed by performing a dot product of the corresponding left row and right column.
What we see in the animation is the scanning of multiplication value vectors inside the cube, each vector producing a summation result at the corresponding position.
Here, the L’s row blocks are filled with 1 (blue) or -1 (red); R’s column blocks are filled similarly. k is 24 here, so the blue values of the result matrix (L @ R) are 24, and the red values are -24.
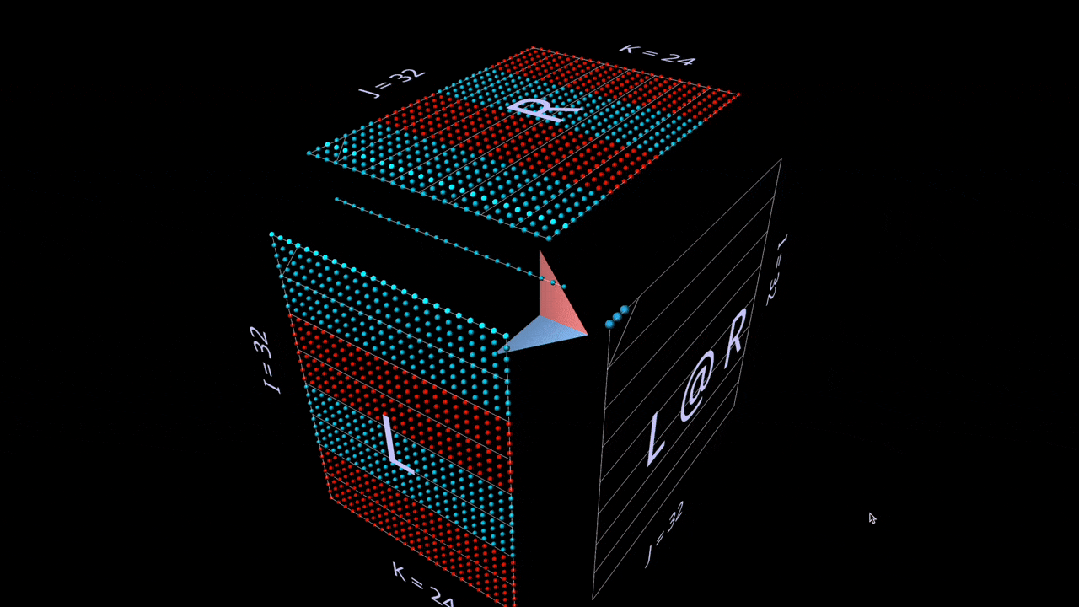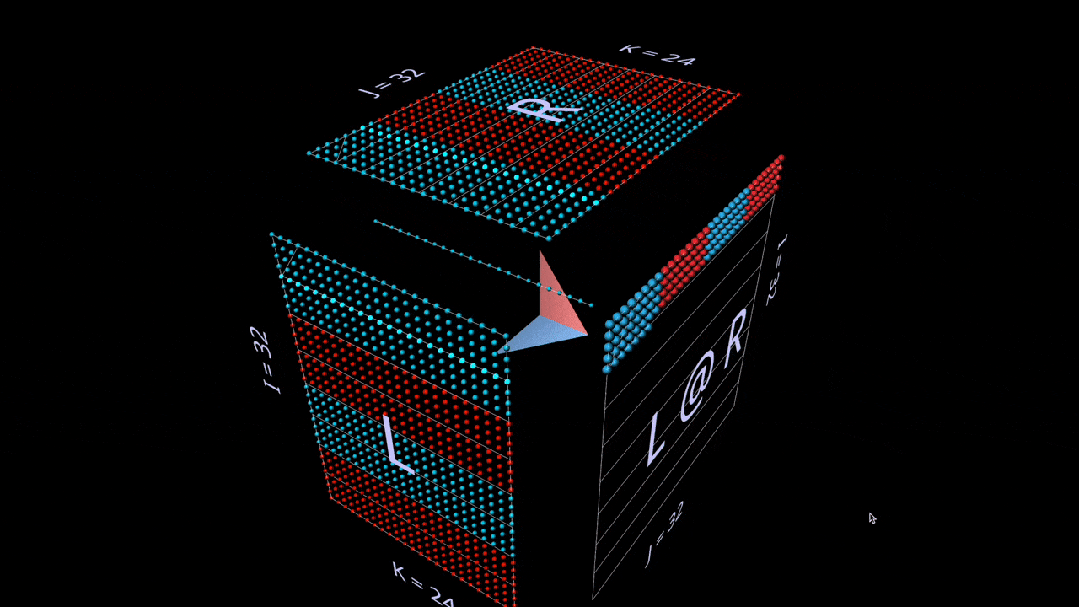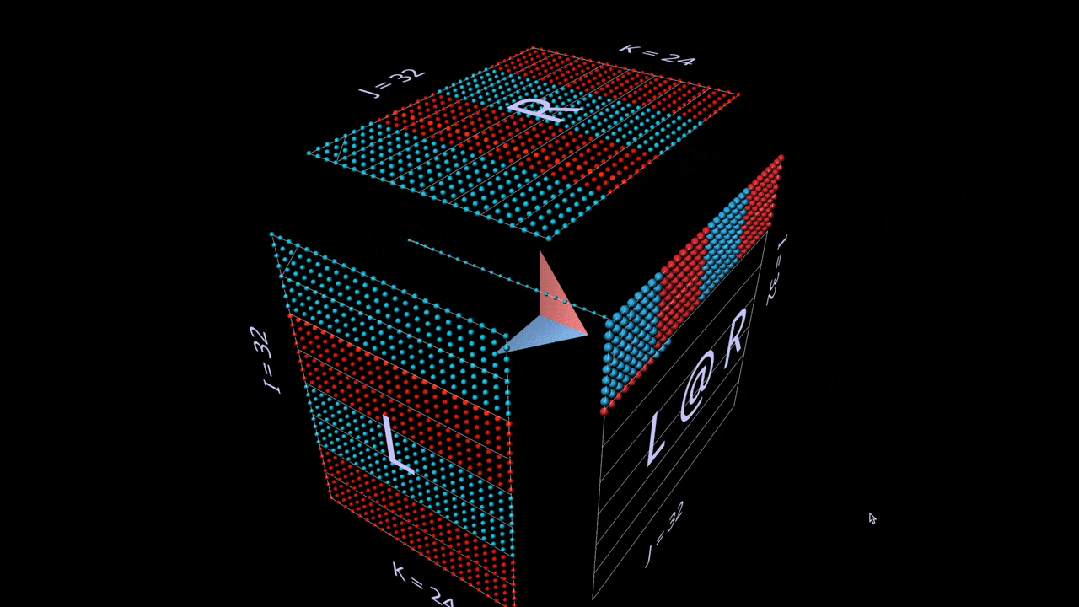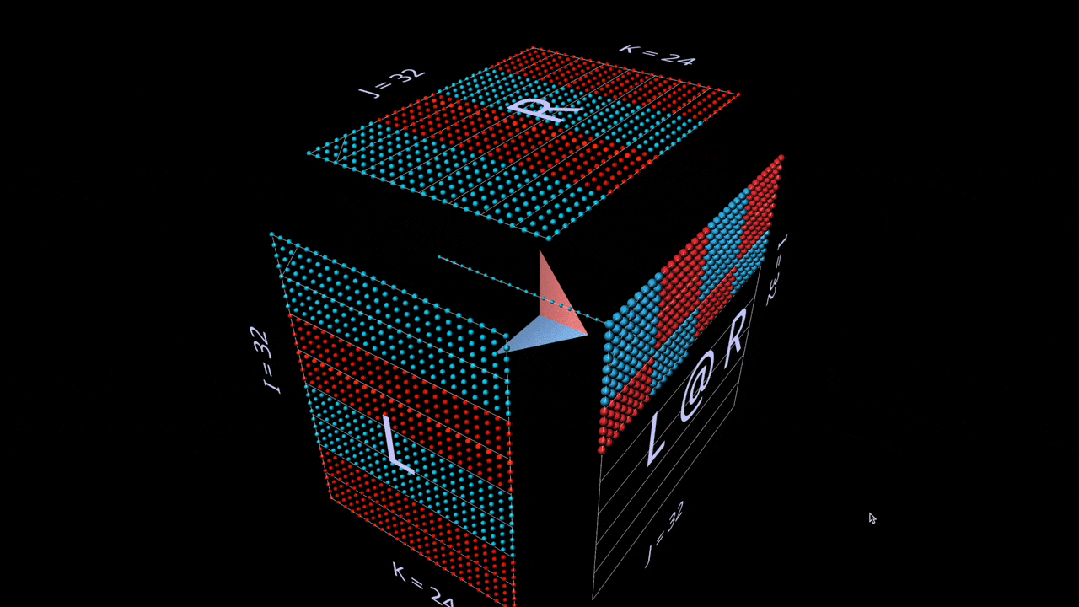
Matrix-Vector Product
The decomposition into a matrix-vector product of matmul looks like a vertical plane (the product of the left parameter with each column of the right parameter), which sweeps horizontally across the inside of the cube, drawing columns onto the result.
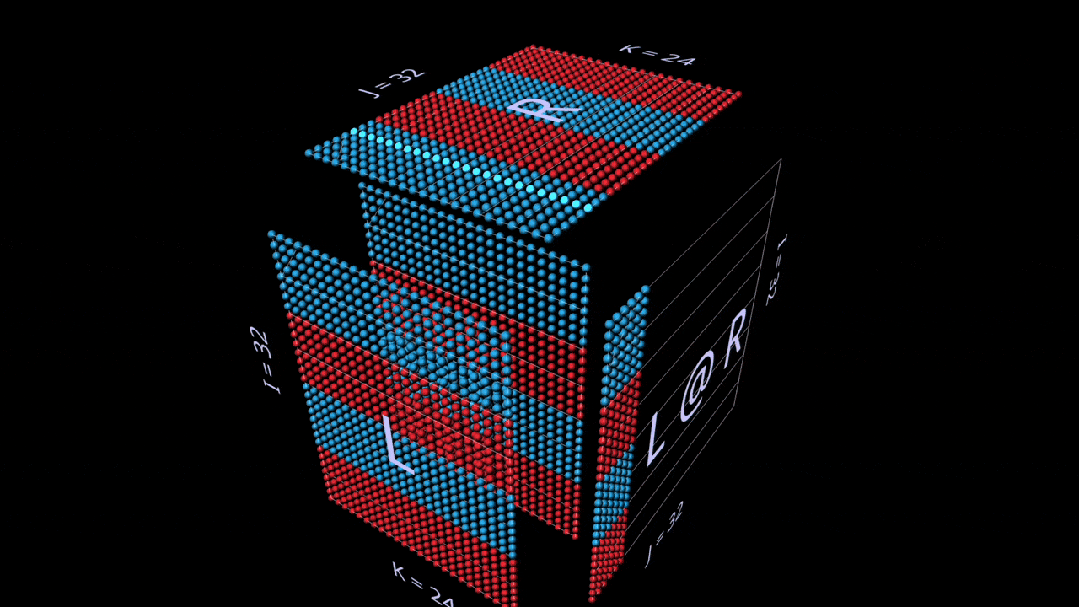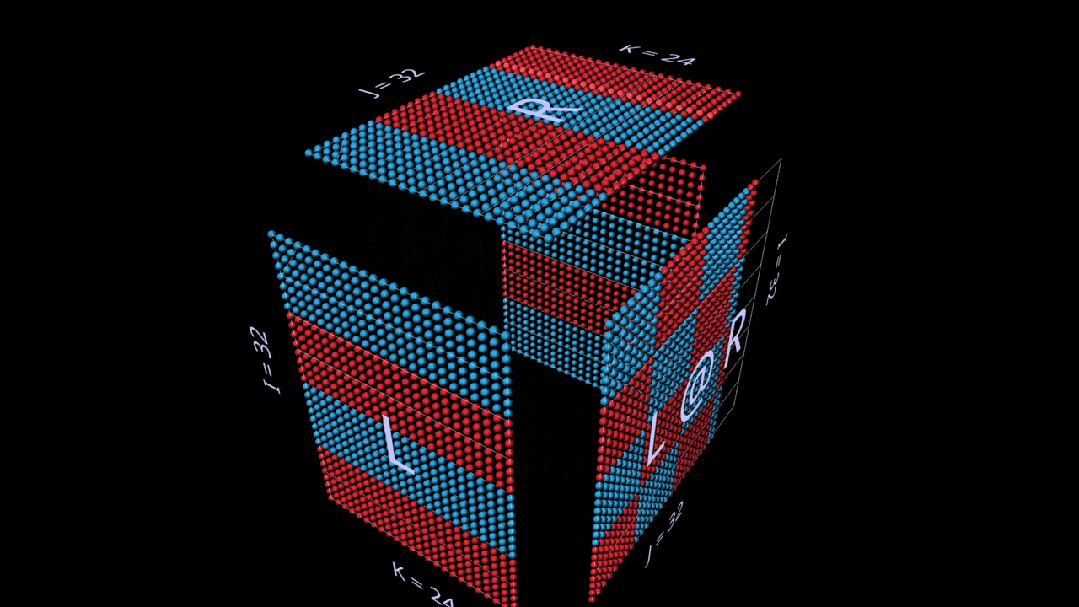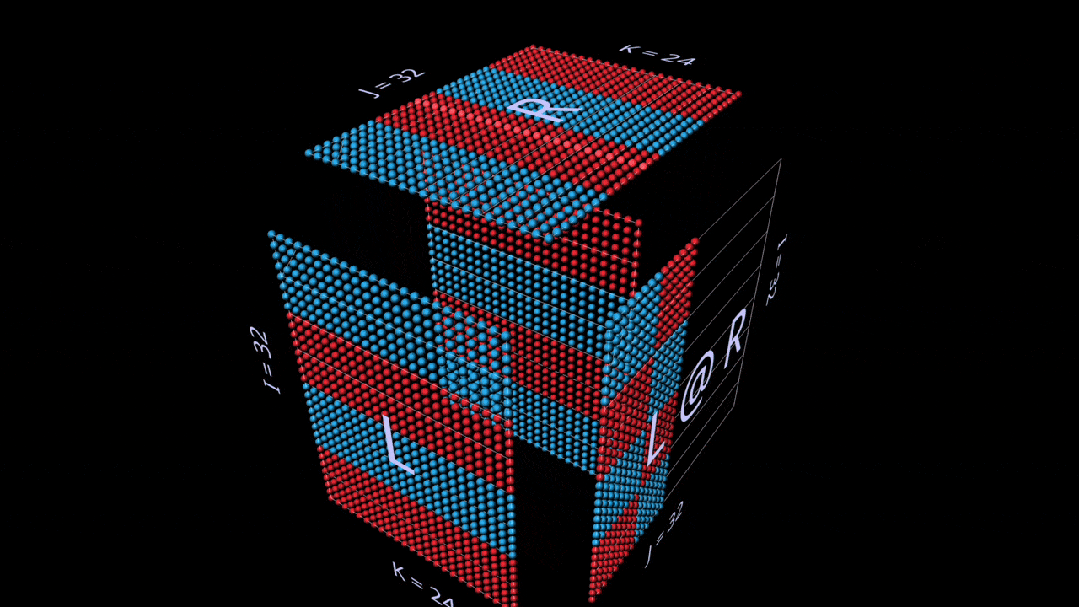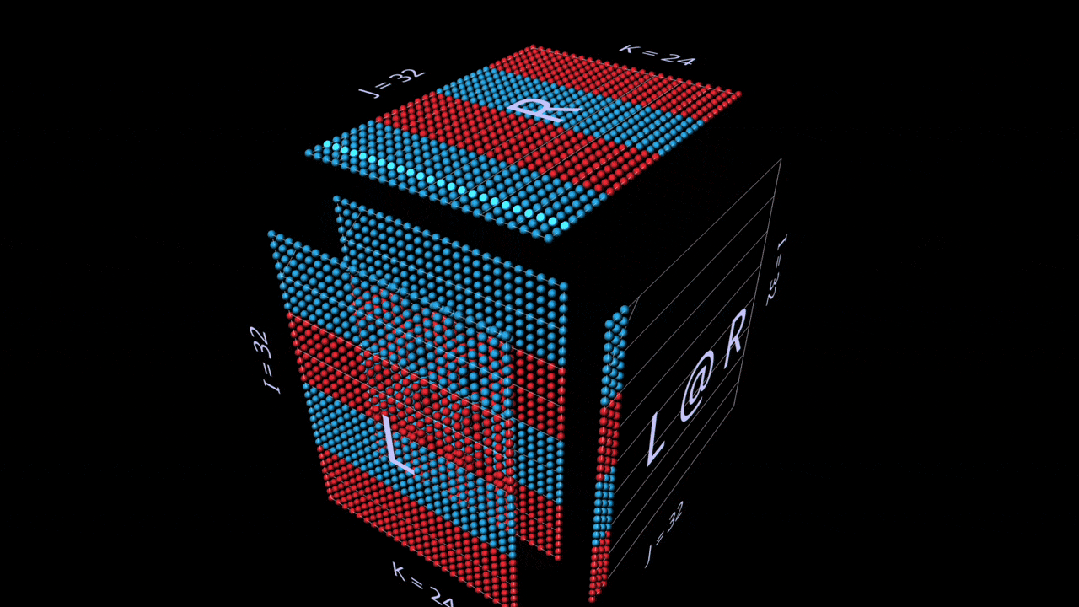
Even in simple examples, observing intermediate values of the decomposition can be very interesting.
For example, when we use randomly initialized parameters, note the prominent vertical patterns in the intermediate matrix-vector product. This reflects that each intermediate value is a scaled copy of the left parameter’s column:

Vector-Matrix Product
The decomposition of matrix multiplication into a vector-matrix product looks like a horizontal plane drawing rows onto the result as it sweeps through the inside of the cube:

Switching to randomly initialized parameters, we see similar patterns to the matrix-vector product, but this time the patterns are horizontal, as each intermediate vector-matrix product is a scaled copy of the right parameter’s row.
When thinking about how matrix multiplication expresses the rank and structure of its parameters, one might consider the situation where both patterns appear simultaneously in the calculations:

Here’s also an intuitive builder using vector matrix products that shows how the identity matrix acts like a mirror, setting its parameters and results at a 45-degree angle:
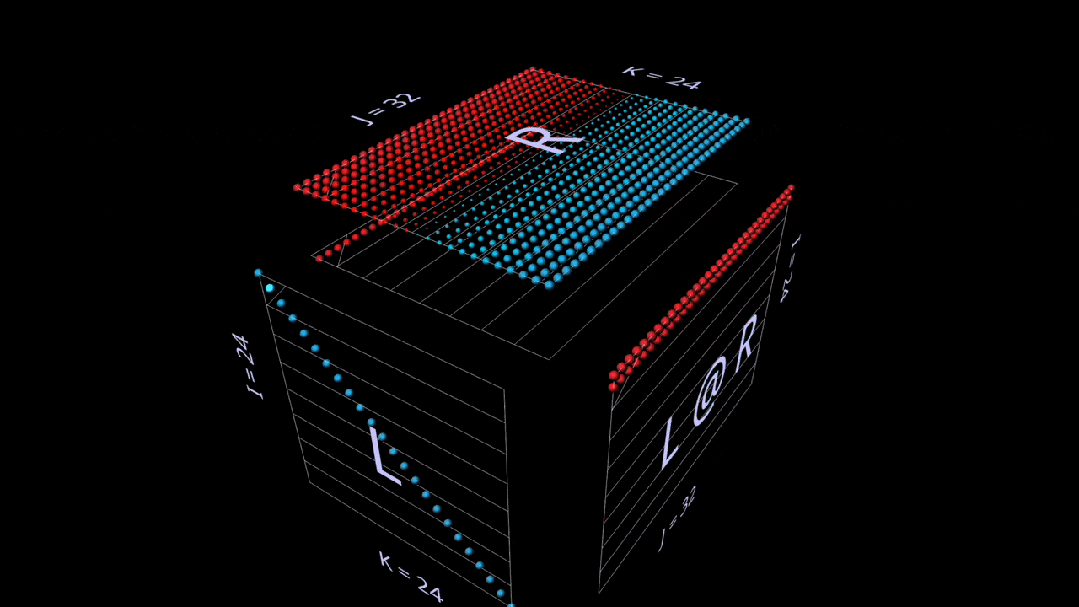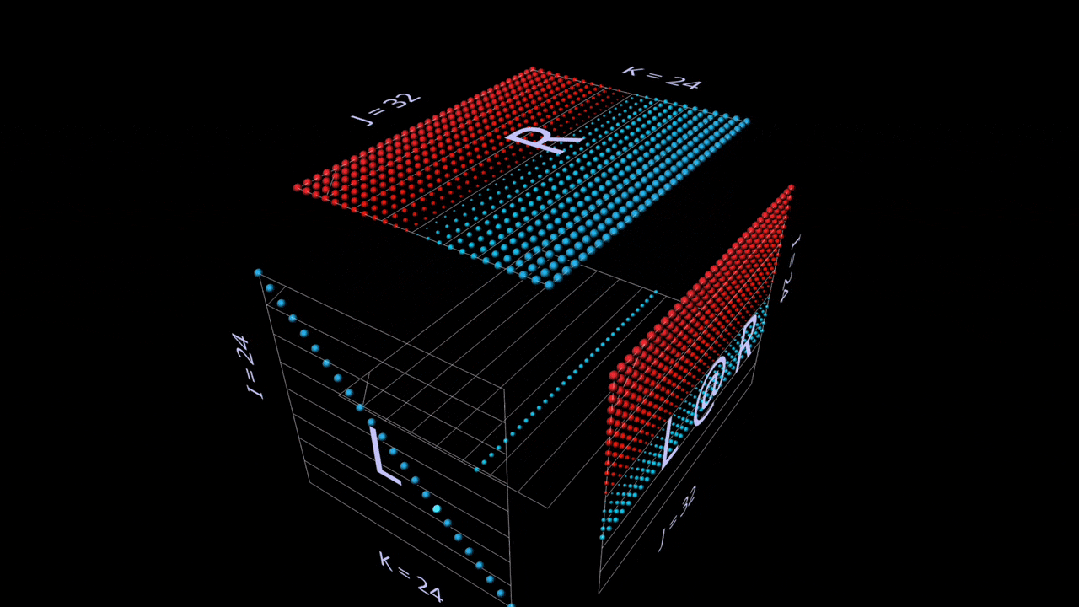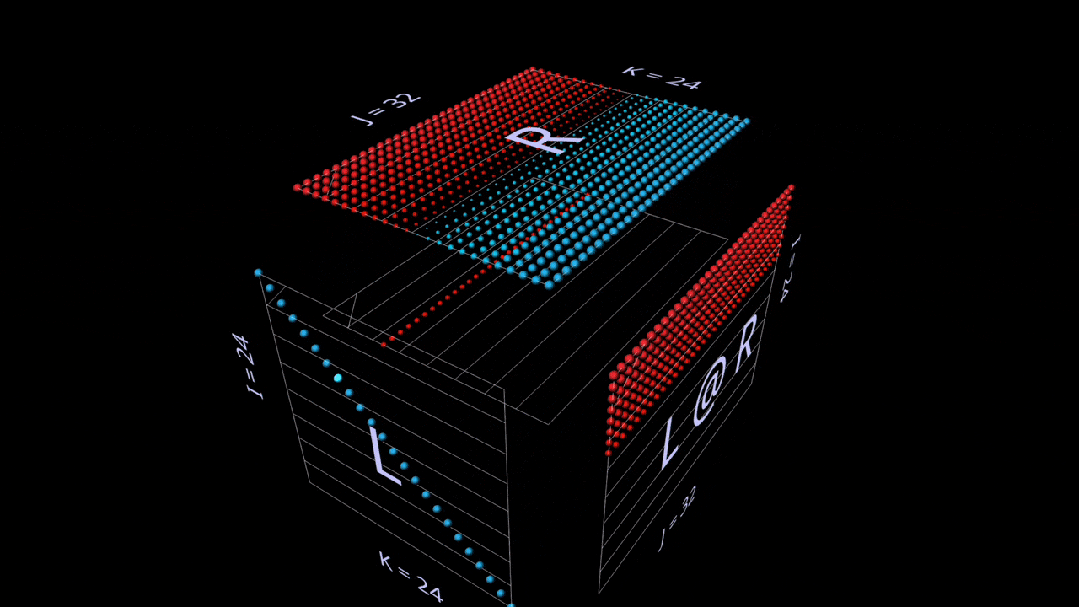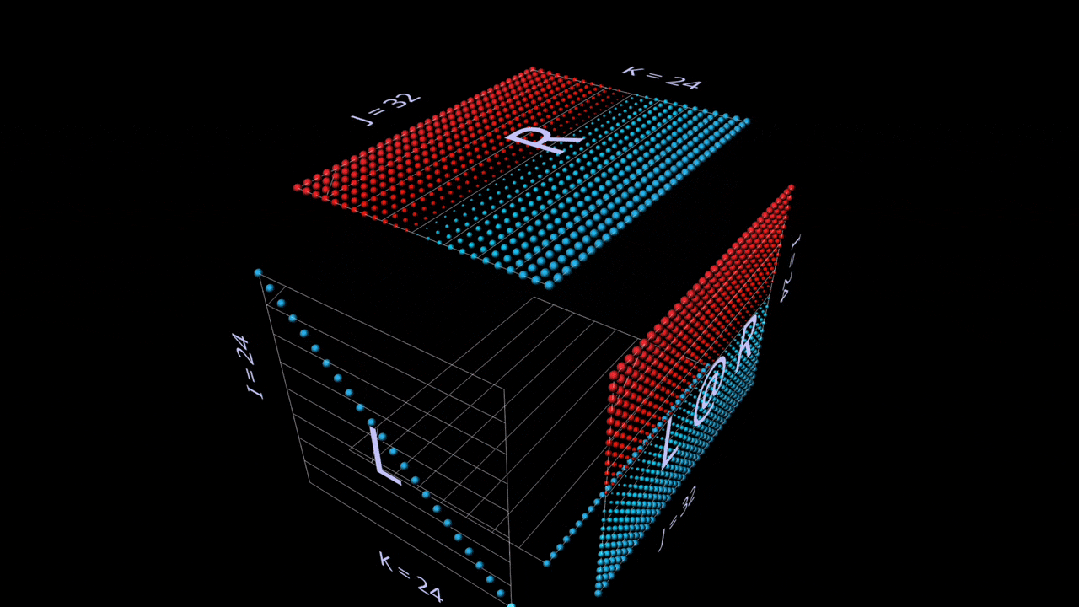
Sum Outer Product
The third plane decomposition proceeds along the k-axis, calculating the matrix multiplication result through the point and outer product of vectors.
Here, we see the outer product plane sweeping “from back to front” across the cube, accumulating into the result:
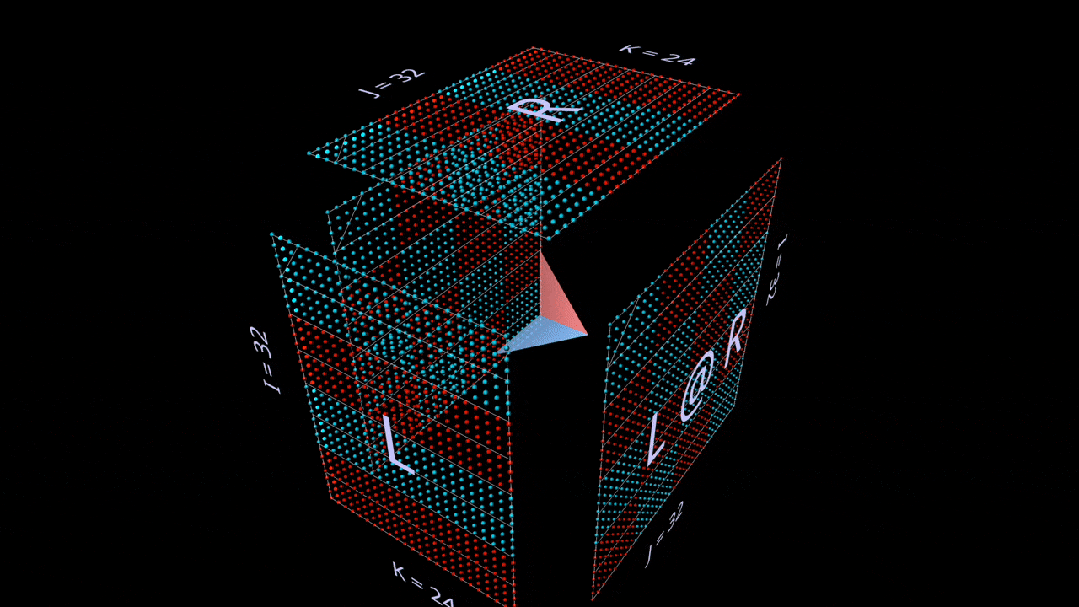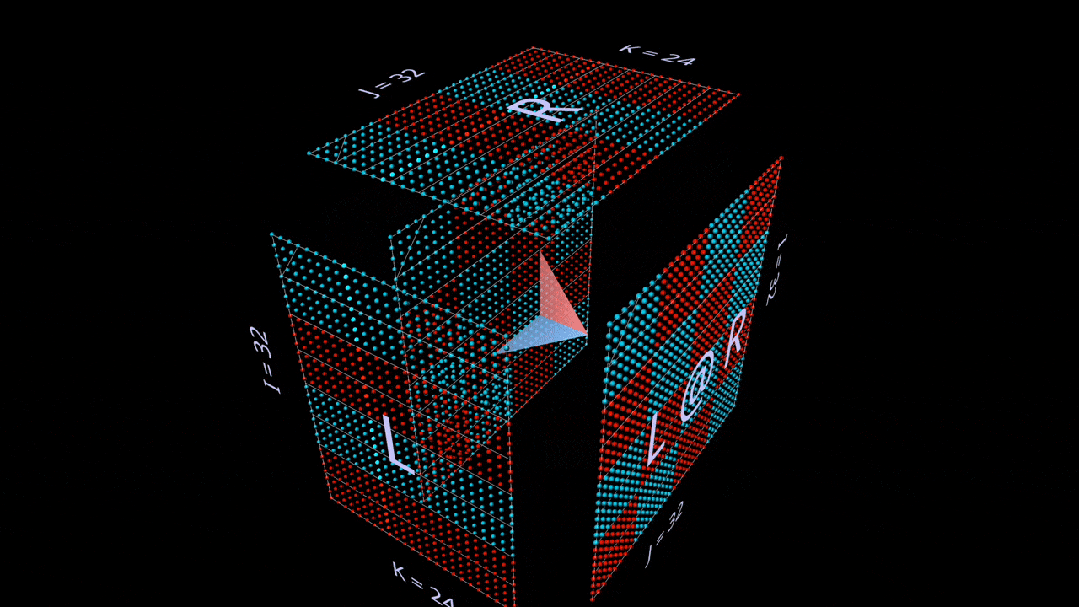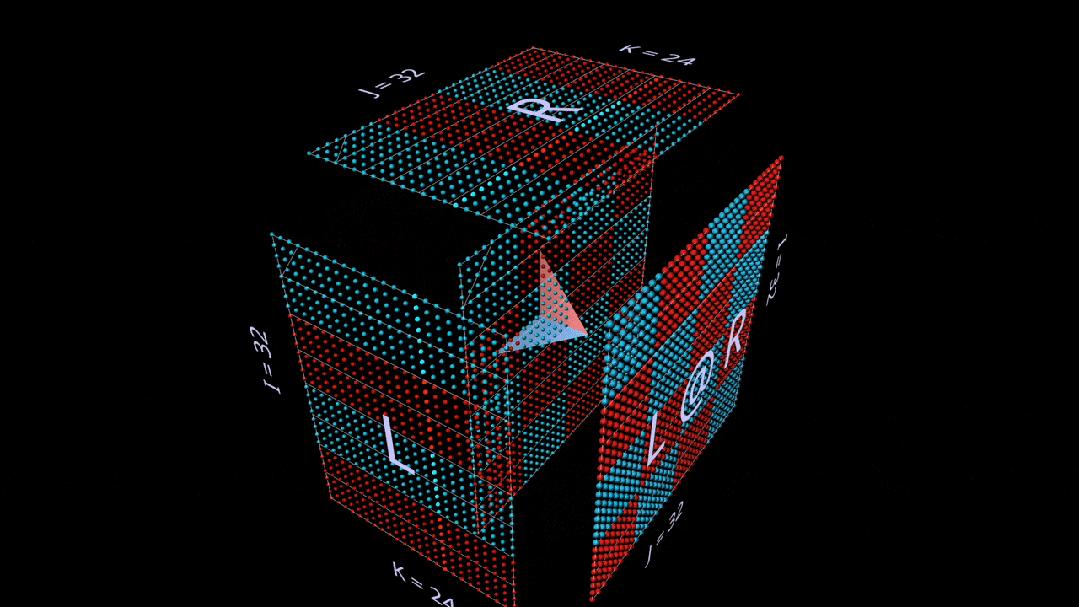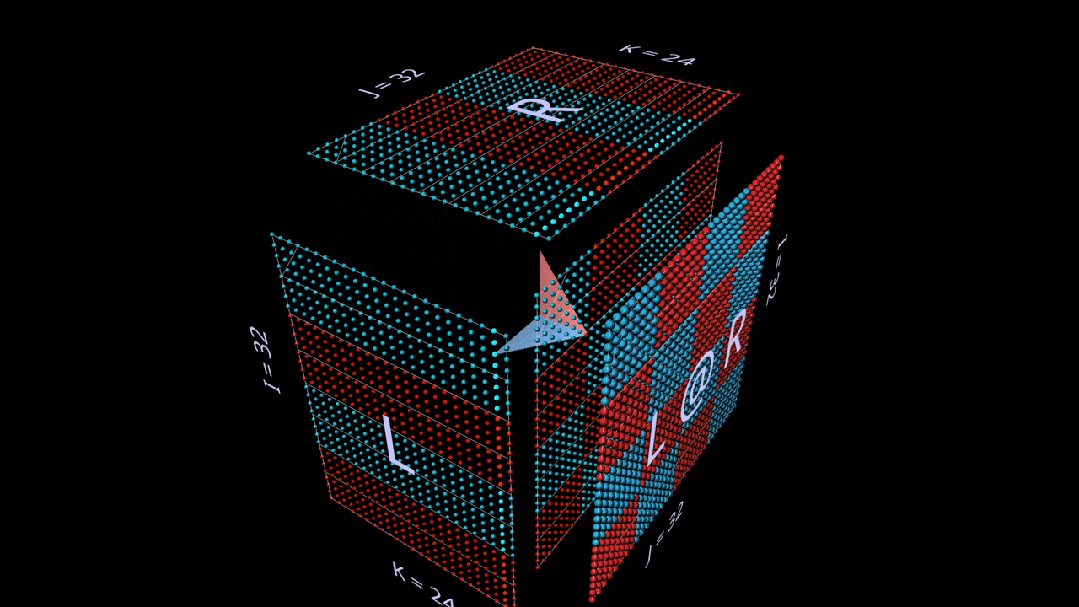
Using randomly initialized matrices for this decomposition, we can see that with each rank-1 outer product, not only values accumulate in the result, but so do ranks.
Among other things, this also helps us understand why “low-rank factorization”, i.e., approximating a matrix by constructing matrix multiplications with very small rank parameters, works best when the matrix being approximated is low-rank.
LoRA will be introduced later:

Expressions
How can we extend this visualization method to combinations of matrix multiplication?
So far, the examples have visualized a single matrix L and R’s multiplication L @ R; what if L and/or R are matrices themselves, and so on?
It turns out we can extend this method well to composite expressions.
The key rule is simple: sub-expressions (sub) matrix multiplications are another cube, subject to the same layout constraints as the parent expression, with the result face of the sub-expression simultaneously being the corresponding parameter face of the parent expression, just like electrons shared in covalent bonds.
Under these constraints, we can freely arrange the faces of sub matmuls.
Here, the researchers used the tool’s default scheme, which alternates between generating convex and concave cubes, a layout that is practically very effective, maximizing space and minimizing occlusion.
In this section, PyTorch will visualize some key components in ML models to become proficient in the visual vocabulary and understand what intuitive feelings even simple examples can bring us.
Left Associative Expressions
First, let’s look at two expressions of the form (A @ B) @ C, each with its unique shape and characteristics.
First, we will endow A @ B @ C with the features of FFN where the “hidden dimension” is wider than the “input” or “output” dimensions. (In this case, this means the width of B is greater than A or C’s width).
As with the single matmul example, floating arrows point to the result matrix, with blue coming from the left parameter and red from the right parameter:

Next, we will visualize A @ B @ C, where the width of B is narrower than A or C, presenting a bottleneck or “autoencoder” shape:
This pattern of alternating convex and concave shapes can be extended to chains of arbitrary lengths: for example, this multi-layer bottleneck:

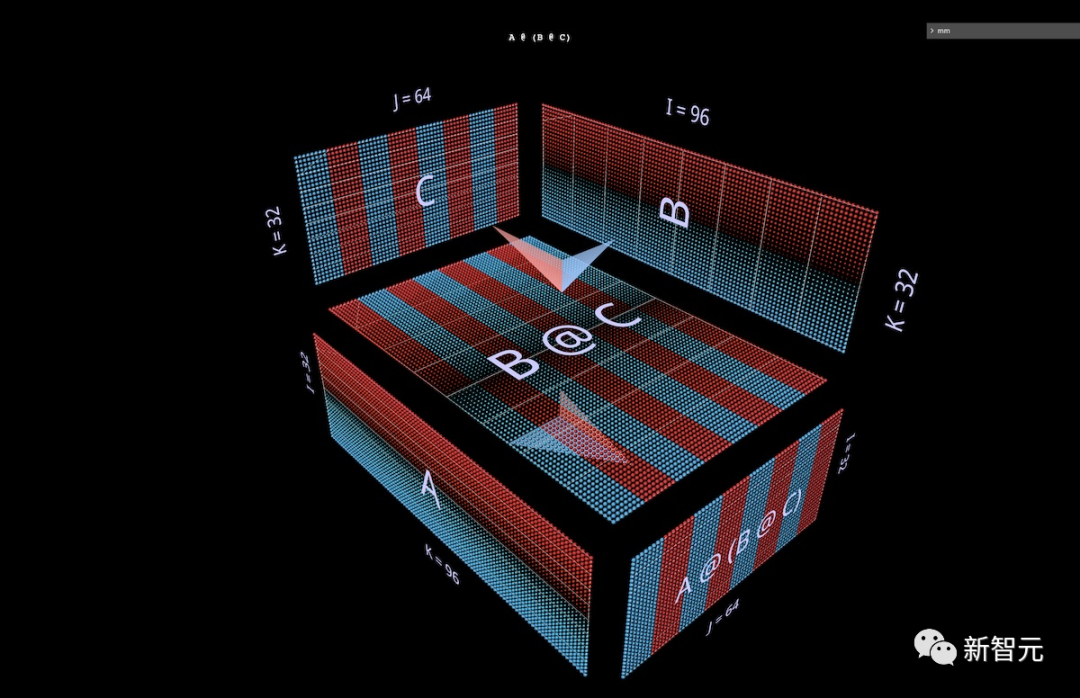
Right Associative Expressions
Next, we will visualize a right associative expression A @ (B @ C).
Sometimes we see MLP adopting a right associative manner, where the input layer is on the right and the weight layers go from right to left.
Using the matrix in the double-layer FFN example above—after appropriate transposition—looks like this, where C now plays the role of the input, B is the first layer, and A is the second layer:
Binary Expressions
For the visualization tool to function beyond simple teaching examples, it must maintain readability as expressions become increasingly complex.
In real-world use cases, binary expressions are a key structural component, where both sides have sub-expressions as matrices.
Here, we will visualize the simplest expression shape, (A @ B) @ (C @ D):

Segmentation and Parallelism
Next, we can illustrate how this visualization style makes the parallel reasoning of composite expressions very intuitive through simple geometric segmentation with two quick examples.
In the first example, we apply standard “data parallel” segmentation to the aforementioned left associative multi-layer bottleneck example.
Segmenting along i, we divide the left initial parameters (batch) and all intermediate results (activations), but do not segment subsequent parameters (weights).
Through the geometry, we can clearly see which participants in the expression are segmented and which remain intact:

The second example demonstrates how to parallelize binary expressions by segmenting the left sub-expression along its j-axis, segmenting the right sub-expression along its i-axis, and segmenting the parent expression along its k-axis:

Inside the Attention Head
Let’s look at a GPT2 attention head—specifically the “gpt2” (small) configuration (layers=12, heads=12, embedding=768) from NanoGPT, using OpenAI weights via HuggingFace.
The input activations come from the forward pass of training samples of 256 tokens from OpenWebText.
The researchers chose it mainly because it computes a fairly common attention pattern and is located in the middle of the model, where the activations have become structured and show some interesting textures.
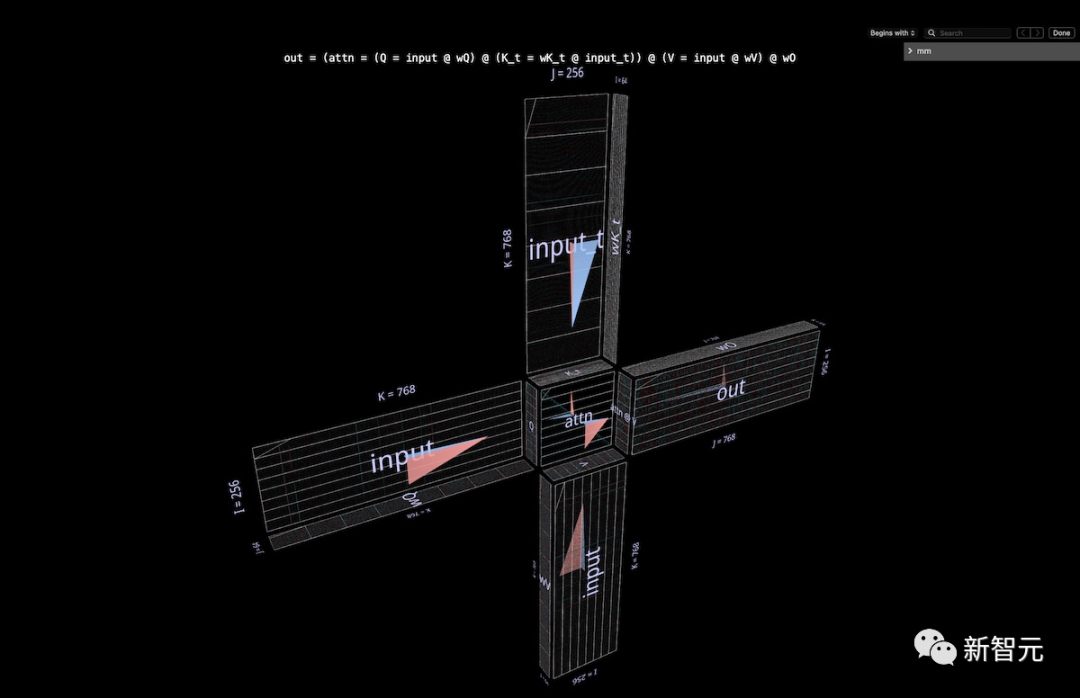
Structure
The entire attention head is visualized as a single composite expression, starting with the input and ending with the projected output. (Note: To keep it self-contained, the researchers performed output projection on each head as described in Megatron-LM).
The computation involves six matrices:
Q = input @ wQ // 1K_t = wK_t @ input_t // 2V = input @ wV // 3attn = sdpa(Q @ K_t) // 4head_out = attn @ V // 5out = head_out @ wO // 6
The thumbnail description of what we are looking at:
The arrow blades are matrix multiplications 1, 2, 3, and 6: the previous group is the inner projection from input to Q, K, and V; the latter group is the outer projection from attn @ V back to the embedding dimension.
In the center is the double matrix multiplication, which first computes the attention scores (the convex cube behind) and then uses them to generate output tokens from the value vector (the concave cube in front). The causal relationship means that the attention scores form a lower triangular.
Calculations and Values
This is an animation of calculating attention. Specifically:
sdpa(input @ wQ @ K_t) @ V @ wO
(i.e., the above matrix 1, 4, 5, and 6, where K_t and V are pre-computed) is a fused vector-matrix multiplication chain: each item in the sequence is completed in one step, from input to attention to output.
Differences Between Heads
Before moving to the next step, here’s another demonstration to give us a simple understanding of how the model works in detail.
This is another attention head of GPT2.
Its behavior is completely different from the 4th head of the 5th layer above, as expected, because it is located in a very different part of the model.
This magnetic head is located in the first layer: layer 0, head 2:

Parallel Attention
We visualize 4 of the 6 matrices in the attention head as a fused vector-matrix multiplication chain.
It is a chain that integrates vector-matrix products, confirming the geometric intuition that the entire left associative chain from input to output is layered along the shared i-axis and can be parallelized.
For example, segmenting along i

Double partitioning

LoRA
The recent LoRA paper describes an efficient fine-tuning technique based on the idea that the weight increments introduced during fine-tuning are low-rank.
According to the paper, this allows us to indirectly train some dense layers in neural networks by optimizing the rank decomposition matrices that change during adaptation while keeping the pre-trained weights frozen.
Basic Idea
In short, the key step is to train factor matrices of the weight matrix instead of the matrix itself: replacing the I x K tensor and K x J tensor’s matmul with the I x J weight tensor, keeping K as some small number.
If K is small enough, the savings in size will be considerable, but the cost is that reducing K will lower the rank that the product can express.
Below is a random left 128 x 4 and right 4 x 128 parameter matmul, which is a rank-4 factorization of the 128 x 128 matrix, quickly illustrating the savings in size and the structural impact on the result. Note the vertical and horizontal patterns of L @ R:

Click to enter—>【Computer Vision and Transformer】Group Chat
ICCV / CVPR 2023 Paper and Code Download
Reply in the background: CVPR2023 to download the open-source paper collection of CVPR 2023 papers and codes.
Reply in the background: ICCV2023 to download the open-source paper collection of ICCV 2023 papers and codes.
The target detection and Transformer group chat has been established.
Scan the QR code below, or add WeChat: CVer333 to add CVer assistant WeChat, and you can apply to join the CVer-target detection or Transformer WeChat group chat. In addition, other vertical directions have been covered: target detection, image segmentation, object tracking, face detection & recognition, OCR, pose estimation, super-resolution, SLAM, medical imaging, Re-ID, GAN, NAS, depth estimation, autonomous driving, reinforcement learning, lane line detection, model pruning & compression, denoising, dehazing, deraining, style transfer, remote sensing images, action recognition, video understanding, image fusion, image retrieval, paper submission & communication, PyTorch, TensorFlow, and Transformer, NeRF, etc.
Be sure to note: research direction + location + school/company + nickname (e.g., target detection or Transformer + Shanghai + Shanghai Jiao Tong University + Kaka), according to the format note, it can be passed more quickly and invited to join the group.
▲ Scan or add WeChat: CVer333 to join the group chat.
CVer Computer Vision (Knowledge Planet) is here! If you want to learn about the latest, fastest, and best CV/DL/AI paper updates, quality practical projects, cutting-edge AI industry information, and materials from beginner to advanced learning tutorials, welcome to scan the QR code below and join CVer Computer Vision, which has gathered thousands of people!
▲ Scan to join the planet.
▲ Click the card above to follow the CVer public account.
Thank you for your likes and views.
