This Article Overview:
1. Background Knowledge
Word2Vec is a type of language model that learns semantic knowledge from a large amount of text data in an unsupervised manner, and is widely used in natural language processing.
Word2Vec is a tool for generating word vectors, and word vectors are closely related to language models. Therefore, we will first understand some knowledge related to language models.
1.1 Statistical Language Models
A statistical language model is a probability model used to calculate the probability of a sentence, usually constructed based on a corpus. So what does it mean to calculate the probability of a sentence? Suppose represents a sentence composed of words in order, then the joint probability of is:
It is called a language model, which is used to calculate the probability of this sentence. Using Bayes’ theorem, the above formula can be decomposed in a chain form:
where the conditional probability is the parameter of the language model. If all these parameters are calculated, then given a sentence, the corresponding probability can be calculated quickly.
It seems simple, right? However, the specific implementation is a bit troublesome. For example, let’s first look at the number of model parameters. Just now, we considered a given sentence of length T, which requires calculating T parameters. Let’s assume the vocabulary size corresponding to the corpus is , then if we consider any sentence of length , theoretically there would be possibilities, and each possibility requires calculating parameters, totaling parameters. Of course, this is just a simple estimation and does not consider duplicate parameters, but this magnitude is still a bit scary. In addition, after calculating these probabilities, they also need to be stored, so storing this information also requires a large memory overhead.
Furthermore, how are these parameters calculated? Common methods include n-gram models, decision trees, maximum entropy models, maximum entropy Markov models, conditional random fields, neural networks, and so on. This article will only discuss the n-gram model and neural networks.
1.2 N-gram Model
Consider the approximate calculation of . Using Bayes’ theorem, we have:
According to the law of large numbers, when the corpus is large enough, can be approximately represented as:
where represents the count of the word string appearing in the corpus, and represents the count of the word string appearing in the corpus. It is conceivable that when is large, the statistics of and will be very time-consuming.
From formula (1), it can be seen that the probability of a word appearing is related to all the previous words. If we assume that the probability of a word appearing is only related to a fixed number of previous words, this is the basic idea of the n-gram model. It makes a Markov assumption of order , believing that the probability of a word appearing is only related to the previous words, that is:
Thus, formula (2) becomes
For example, if , we have
This simplification not only makes the statistics of individual parameters easier (the word strings that need to be matched during statistics are shorter), but also reduces the total number of parameters.
So, how large should the parameters in the n-gram be? Generally speaking, the selection of needs to consider both computational complexity and model performance.
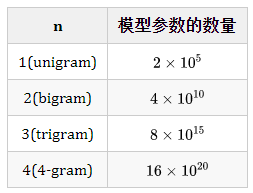
Table 1: The relationship between the number of model parameters and n
In terms of computational complexity, Table 1 shows how the number of model parameters in the n-gram model changes with the gradual increase of , assuming a vocabulary size of (the vocabulary size of Chinese is roughly this magnitude). In fact, the magnitude of model parameters is an exponential function of ( ), obviously cannot be too large, and in practical applications, at most a trigram model of is used.
In terms of model performance, the larger is, the better the performance is theoretically. Nowadays, the massive data on the Internet and the improvement of machine performance make it possible to compute higher-order language models (such as ), but it should be noted that when reaches a certain level, the increase in model performance will diminish. For example, when increasing from to , the performance increases significantly, while increasing from to does not show significant improvement (specific references can be found in Wu Jun’s book “Mathematics in Beauty”). In fact, there is also a trade-off between reliability and distinguishability; the more parameters there are, the better the distinguishability, but at the same time, the fewer instances for each parameter, which reduces reliability, so a balance needs to be struck between reliability and distinguishability.
In addition, there is an important step called smoothing in the n-gram model. Returning to formula (3), consider two questions:
-
If , can we consider that is equal to ? -
If = , can we consider that is equal to ?
Clearly, this is not possible, but it is an unavoidable problem, no matter how large your corpus is. Smoothing techniques are used to address this issue, which will not be discussed here.
In summary, the n-gram model is a model whose main work is to count the occurrences of various word strings in the corpus and smooth them. Once the probability values are calculated, they are stored, and when the probability of a sentence needs to be calculated next time, simply find the relevant probability parameters and multiply them together.
However, in the field of machine learning, there is a general method for solving problems: after modeling the problem under consideration, first construct a target function for it, then optimize this target function to obtain a set of optimal parameters, and finally use the model corresponding to this set of optimal parameters for prediction.
For statistical language models, using maximum likelihood, we can set the target function as:
where represents the corpus, and represents the context of the word, that is, the set of surrounding words. When empty, we take . Specifically, for the n-gram model introduced earlier, we have .
Of course, in practical applications, maximum log-likelihood is often used, that is, the target function is set as
and then maximize this function.
From formula (4), it can be seen that the probability has been regarded as a function of and , that is:
where is the set of parameters to be determined. Once the optimal parameter set is obtained by optimizing formula (4), it is uniquely determined, and any probability can be calculated through function in the future. Compared to n-gram, this method does not require pre-calculating and storing all probability values, but obtains them through direct calculation, and by selecting an appropriate model, the number of parameters in can be much smaller than the number of model parameters in n-gram.
It is clear that the key to such a method is the construction of the function. The next subsection will introduce a method constructed through neural networks. The reason for specifically introducing this method is that it can be seen as the predecessor or foundation of the algorithm framework in Word2Vec.
1.3 Neural Probabilistic Language Model
This subsection introduces a neural probabilistic language model proposed by Bengio et al. in their 2003 paper “A Neural Probabilistic Language Model.” This paper was the first to propose using neural networks to solve language model problems. Although it did not receive much attention at the time, it laid a solid foundation for later deep learning in solving language model problems and many other NLP problems. Subsequent researchers, standing on the shoulders of Yoshua Bengio, have made more achievements. This includes Tomas Mikolov, the author of Word2Vec, who proposed RNNLM and later Word2Vec based on NNLM. The paper also early proposed representing words as low-rank vectors rather than One-Hot. Word embedding, as a by-product of a language model, played a key role in later research, providing researchers with broader ideas. It is worth noting that the concept of Word2Vec was also proposed in this paper.
What is a word vector? Simply put, it is a fixed-length real-valued vector assigned to any word in the vocabulary, and the length of this vector is called the word vector. Further understanding of word vectors will be discussed in the next section.
Since it is a neural probabilistic language model, it must use neural networks. The following figure shows the structure of the neural network. The model consists of three layers: the first layer is the mapping layer, which maps the words to the corresponding concatenated word embeddings; in fact, this layer is the input layer of an MLP; the second layer is the hidden layer, with the activation function ; the third layer is the output layer, because it is a language model, it needs to predict the next word based on the previous word, so it is a multi-class classifier using . The largest computational load of the entire model is concentrated in the last layer, because generally speaking, the vocabulary is large, and it needs to compute the conditional probability of each word, which is the computational bottleneck of the entire model.
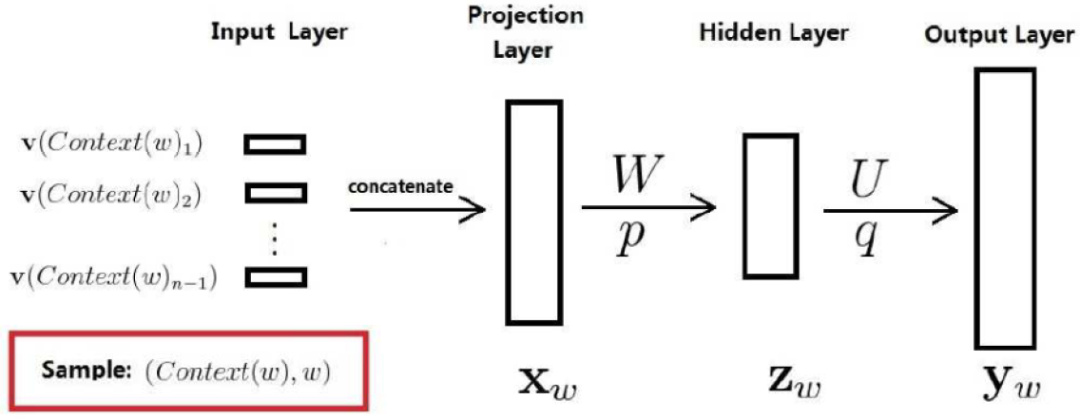
After the above steps of calculation, the obtained is just a vector of length , and its components cannot represent probabilities. If we want the component of to represent the probability that the next word is the word given the context , we still need to perform a Softmax normalization, after normalization, it can be represented as:
where represents the index of the word in the vocabulary.
Here, it is necessary to initialize a word embedding matrix in advance, with each row representing the vector of a word. Word vectors are also training parameters and are updated during each training. Here we can see that word vectors are a by-product of the language model, because the work of the language model itself is to estimate how similar a given sentence is to human language, but later research found that language models became a very good tool.
Softmax is a very inefficient processing method, requiring first to calculate the probability of each word and also to calculate the exponent, which is approximated using series in computers, leading to high computational complexity, and finally performing normalization. Many subsequent studies have optimized this problem, such as hierarchical softmax and softmax tree.
Of course, the effect of NNLM does not seem significant now, but it is of great importance for subsequent related research. The paper’s Future Work mentions that using RNN instead of MLP as the model may achieve better results, which was verified later in Tomas Mikolov’s doctoral thesis, which is the later RNNLM.
What advantages does the neural probabilistic language model have compared to the n-gram model? There are mainly two points:
-
The similarity between words can be reflected through word vectors.
For example, if a certain (English) word appears times, while appears times. According to the n-gram model, the probability of must be much greater than that of . Note that the only difference between and is that they are “dog” and “cat”, and these two words play similar roles both syntactically and semantically, so and should be very close. In fact, the values of and calculated by the neural probabilistic language model are roughly equal. The reason is that: (1) in the neural probabilistic language model, it is assumed that the word vectors of similar words are also similar; (2) the probability function is smooth with respect to word vectors, meaning that a small change in the word vector only causes a small change in probability. Thus, for the following sentences, as long as one appears in the corpus, the probabilities of the other sentences will also increase accordingly.
A dog is running in the room. A cat is running in the room. The cat is running in a room. A dog is walking in a bedroom. The dog was walking in the room.
-
The model based on word vectors has a built-in smoothing function (as seen from formula (5), will not be zero), thus eliminating the need for additional processing like in n-gram.
Finally, let’s think back to the role of word vectors in the entire neural probabilistic language model. During training, they are used as auxiliary parameters to help construct the target function, and after training is completed, they seem to be just a by-product of the language model. But this by-product should not be underestimated; the next section will elaborate further.
2. Word Vectors
In natural language processing-related tasks, natural language needs to be handled by algorithms in machine learning, which usually requires mathematical representation of language because machines do not recognize human language, they only recognize mathematical symbols. Vectors are the main way humans abstract things from the real world and present them to machines, so it can be said that vectors are the primary means of inputting data into machines.
Word vectors are a way to mathematically represent words in language, as the name suggests, a word vector represents a word as a vector. We all know that words need to be encoded into numerical variables before being fed into neural network training, and there are two common encoding methods: One-Hot Representation and Distributed Representation.
2.1 One-Hot Representation
A very simple way to represent word vectors is One-Hot encoding, which uses a long vector to represent a word, where the length of the vector is equal to the size of the vocabulary, and there is only one in the vector, with all others being , and the position of corresponds to the position of the word in the vocabulary.
For example: I like writing code, then the one-hot encoding would be:
| Word | One-Hot Encoding |
|---|---|
| I | 1 0 0 0 |
| like | 0 1 0 0 |
| writing | 0 0 1 0 |
| code | 0 0 0 1 |
This One-Hot encoding, if stored in a sparse manner, can be very concise: that is, assigning a numerical ID to each word. For example, in the above example, code is assigned , like is assigned . If programming implementation is needed, a hash table can be used to assign a number to each word. Such a concise representation, combined with algorithms such as maximum entropy, SVM, CRF, etc., can already perform well in various mainstream tasks in the NLP field.
However, this representation of words has three disadvantages:
(1) It is prone to the curse of dimensionality, especially when used in some algorithms for Deep Learning;
When your vocabulary reaches tens of millions or even hundreds of millions, you will encounter a more serious problem, dimensional explosion. Here, using words, you will find that we used four dimensions, and when the number of words reaches tens of millions, the size of the word vector becomes tens of millions of dimensions. Not to mention anything else, just the memory cannot handle such a large word vector. Assuming you use one bit to represent each dimension, then a single word would need about GB of memory, but note that this is just for one word, and there will be tens of millions of words, so memory will explode.
(2) Vocabulary gap, unable to accurately represent the similarity between words;
Any two words are isolated, and from these two vectors, it is impossible to see whether there is a relationship between the two words. For example, the relationship between I and like and the relationship between like and writing cannot be represented by and and and . You will find that One-Hot encoding cannot express any relationship between words at all.
(3) Strong sparsity;
When the dimensions grow excessively, you will find that there are many zeros, resulting in very little useful information in the entire vector, making it almost impossible to perform calculations.
Due to these various issues with One-Hot encoding, researchers sought to develop another way to represent words, which is Distributed Representation.
2.2 Distributed Representation
Distributed Representation was first proposed by Hinton in 1986, which can overcome the above disadvantages of One-Hot Representation. The basic idea is: through training, map each word in a certain language to a fixed-length short vector (of course, here, “short” is relative to the “long” of One-Hot Representation), and all these vectors form a word vector space, where each vector can be regarded as a point in that space. By introducing “distance” in this space, we can determine the syntactic and semantic similarity between words based on the distance between them. The word vectors used in Word2Vec adopt this Distributed Representation.
Why is it called Distributed Representation? Many people ask this question. A simple explanation is this: for One-Hot Representation, the vector has only one non-zero component, which is very concentrated (a bit like putting all eggs in one basket); whereas for Distributed Representation, the vector has many non-zero components, which are relatively scattered (a bit like spreading the risk), distributing the information of the word across various components. This is similar to distributed parallel computing.
How to obtain word vectors? Many different models can be used to estimate word vectors, including the well-known LSA (Latent Semantic Analysis) and LDA (Latent Dirichlet Allocation). In addition, using neural network algorithms is also a common method, and the neural probabilistic language model introduced in the previous section is a good example. In that model, the goal is to generate a language model, and the word vector is merely a by-product. In fact, in most cases, word vectors and language models are bundled together, obtained simultaneously after training. The most classic paper on training language models using neural networks is the one published by Bengio in 2003 titled “A Neural Probabilistic Language Model,” which was followed by a series of related research works, including the Word2Vec from Tomas Mikolov’s team at Google.
3. Word2Vec Network Structure
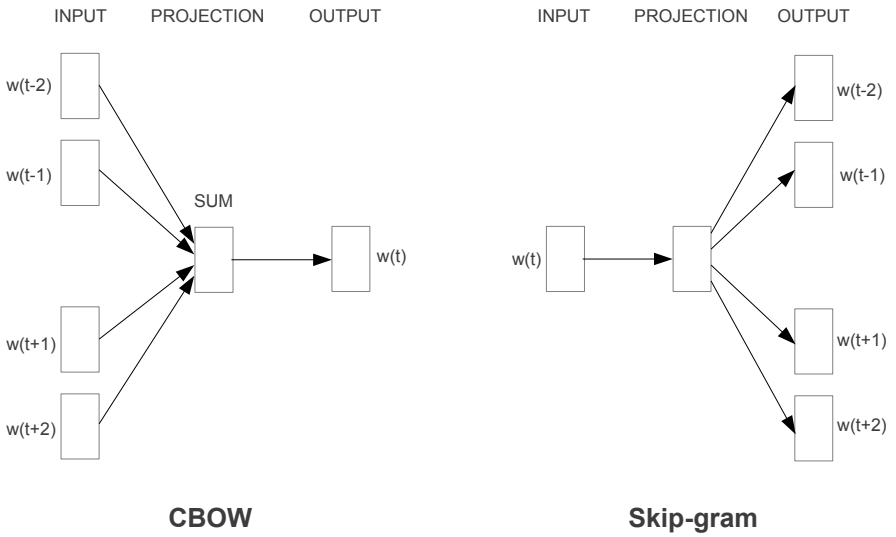
Word2Vec is a lightweight neural network, whose model consists only of an input layer, a hidden layer, and an output layer. The model framework mainly includes CBOW and Skip-gram models based on different inputs and outputs. The CBOW method predicts the current word given the context of words, while Skip-gram predicts the context of words given the current word, as shown in the figure below:
3.1 CBOW
3.1.1 Simple CBOW Model
To better understand the principles inside the model, we will start with the Simple CBOW model (which takes one word as input and outputs one word).
As shown in the figure above:
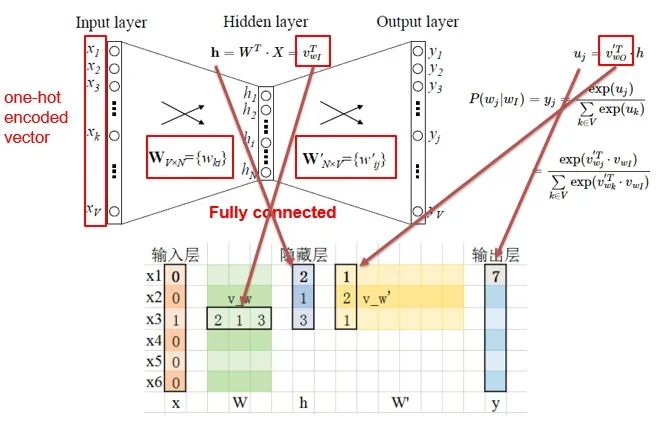
-
The input layer X is the one-hot representation of the word (considering a vocabulary, where each word has a number, then the one-hot representation of the word is a vector of dimension , where the th element is non-zero, and all other elements are zero, for example: ). -
There is a weight matrix between the input layer and the hidden layer, and the value obtained by the hidden layer is obtained by multiplying the input with the weight matrix (attentive readers will notice that multiplying a vector by a matrix is equivalent to selecting a certain row of the weight matrix, as shown in the figure: the input vector is , and its transpose multiplied by the weight matrix is equivalent to selecting the th row as the value of the hidden layer). -
There is also a weight matrix from the hidden layer to the output layer, so each value of the output layer vector is actually the dot product of the hidden layer vector with each column of the weight vector. For example, the first number of the output layer is the result of the dot product of the vector with the th column vector. -
The final output needs to go through the softmax function, normalizing each element in the output vector to a probability between and , where the highest probability is the predicted word.
After understanding the model framework of the Simple CBOW model, let’s learn about its objective function.
The output layer, through softmax normalization, represents the raw output of the output layer. Through the following formula, our objective function can be transformed into its current form:
3.1.2 CBOW Multi-Word Context Model
After understanding the Simple CBOW model, it is easy to expand to the CBOW model, which is just replacing a single input with multiple inputs (the part marked in red).
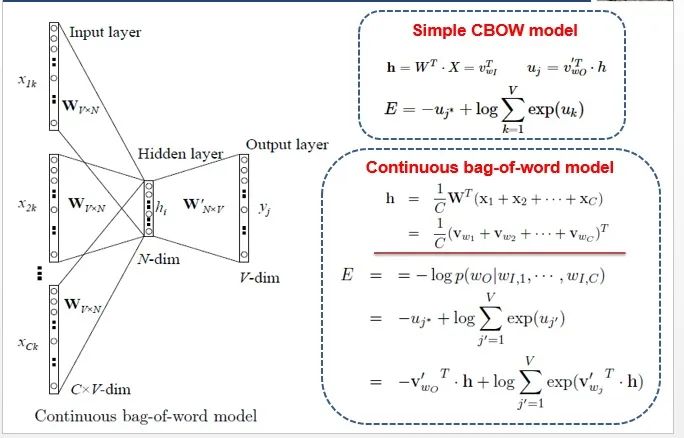
Comparing, it can be found that unlike the simple CBOW, the input has changed from one word to multiple words, and each input reaches the hidden layer through the same weight matrix, and the value of the hidden layer becomes the average of multiple words multiplied by the weight matrix.
3.2 Skip-gram Model
With the introduction of CBOW, understanding the Skip-gram model should be quicker.
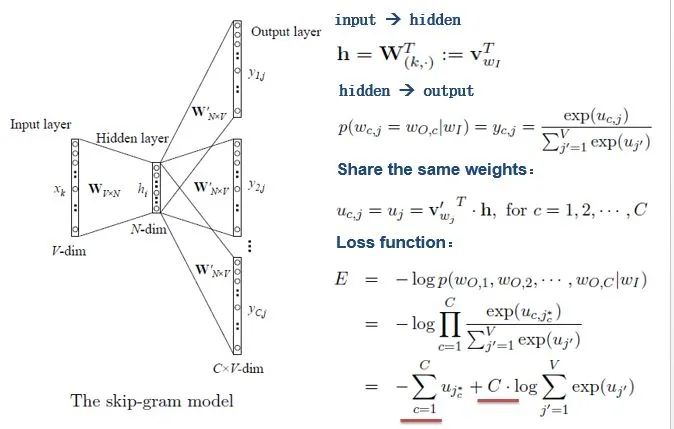
As shown in the figure above, the Skip-gram model predicts the probabilities of multiple words by inputting one word. The principle from the input layer to the hidden layer is the same as that of the simple CBOW, but different is that from the hidden layer to the output layer, the loss function becomes the total loss function of words, and the weight matrix is still shared.
Generally, neural network language models predict the probabilities of the target words, meaning that each prediction must be computed based on the entire dataset, which undoubtedly incurs significant time overhead. Unlike other neural networks, Word2Vec proposes two ways to speed up training, one is Hierarchical softmax, and the other is Negative Sampling.
4. Model Based on Hierarchical Softmax
The model based on hierarchical softmax mainly includes input layer, projection layer (hidden layer), and output layer, which is very similar to the structure of a neural network. For the CBOW model based on hierarchical softmax in Word2Vec, the final objective function to optimize is:
where represents the context words of the word . The final objective function to optimize for the Skip-gram model based on hierarchical softmax is:
4.1 Hierarchical Softmax for CBOW
4.1.1 CBOW Model Network Structure
The following figure shows the overall structure of CBOW based on hierarchical softmax, which includes input layer, projection layer, and output layer:
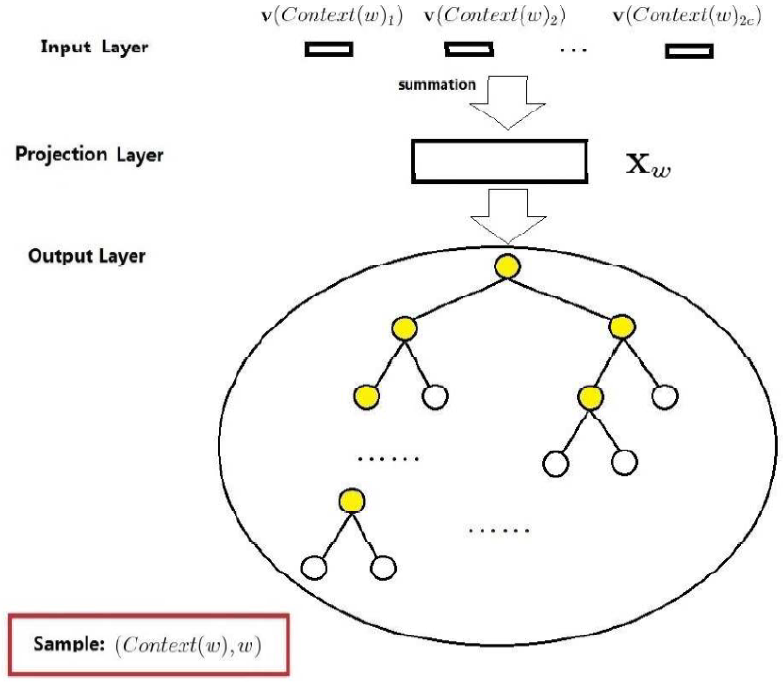
-
The input layer refers to the word vectors of the words contained in . -
The projection layer is where the word vectors are directly summed, resulting in the following:
-
The output layer is a Huffman tree, where the leaf nodes correspond to the words, and there are non-leaf nodes (the nodes marked in yellow in the above figure). The essence of the Word2Vec method based on hierarchical softmax is concentrated in this Huffman tree part, which will be introduced in detail below.
4.1.2 Objective Function of CBOW
To facilitate the following introduction and formula derivation, we need to predefine some variables:
-
: the path from the root node to the leaf node corresponding to the word . -
: the number of nodes contained in the path . -
: the nodes corresponding to the path , where represents the root node and represents the node corresponding to the word . -
: the Huffman code corresponding to the word , which is composed of bits, represents the th bit corresponding to the node in the path , and the root node does not participate in the corresponding encoding. -
: the vector corresponding to the non-leaf nodes in the path , where represents the vector corresponding to the th non-leaf node in the path . The reason for defining word vectors for non-leaf nodes is that the word vectors of these non-leaf nodes will be used as auxiliary variables in the calculation of the following formulas.
Now that we have introduced so many symbols, let’s illustrate them with a simple example, considering the case where the word =”football”. The red line in the following figure is the path taken by our word, and the nodes along the entire path constitute the path , which has a length of , and then is the five nodes along the path , where corresponds to the root node. The Huffman code corresponding to “football” is . Finally, is the vector corresponding to the non-leaf nodes along the path .
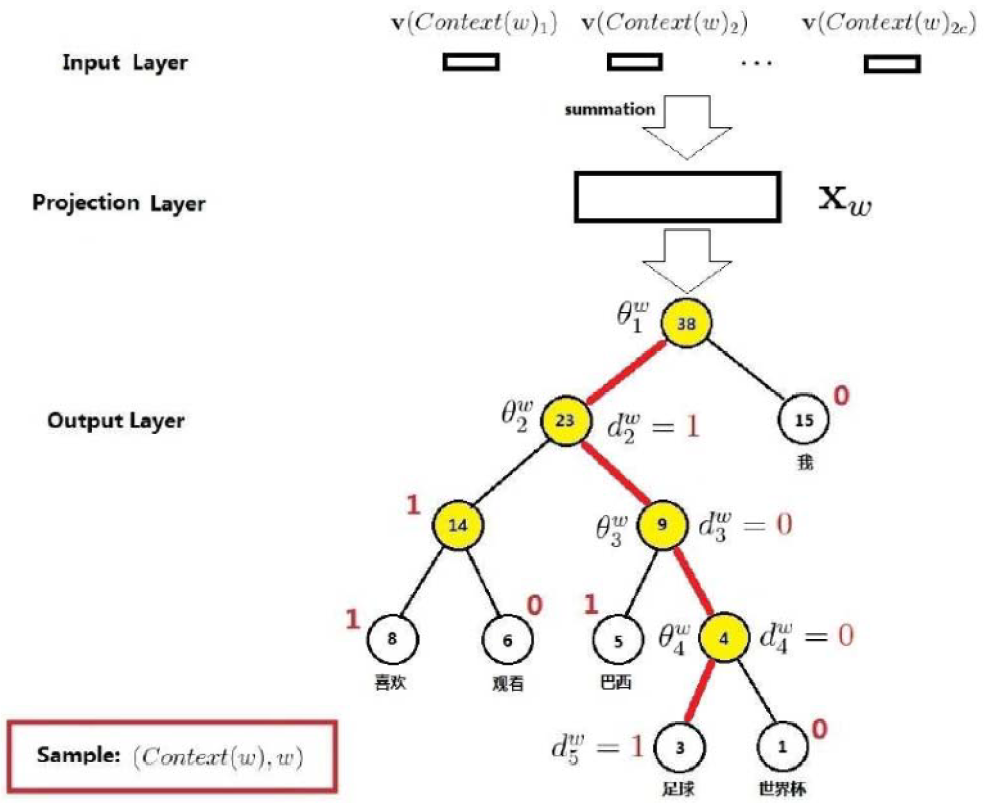
Next, we need to consider how to construct the conditional probability function . Taking the example of =”football”, the red line represents the path taken to reach the leaf node “football”, which goes through branches, corresponding to binary classifications at each branch.
Since it is a binary classification, we can define one as the positive class and the other as the negative class. The Huffman code for “football” is , which does not include the root node, because the root node cannot be classified as either left or right subtree. According to the Huffman code, we can generally consider the positive class as the nodes in the Huffman code, while the negative class can be considered as the nodes not in the Huffman code. However, this is merely a convention, as there is no explicit requirement for correspondence between the Huffman code and positive and negative classes. In fact, Word2Vec defines the nodes corresponding to as the negative class and those corresponding to as the positive class, meaning that if classified to the left subtree, it is the negative class; if classified to the right subtree, it is the positive class. Thus, we can define a formula for positive and negative classes:
In short, when classifying a node, if it goes left, it is the negative class, and if it goes right, it is the positive class.
When performing binary classification, the Sigmoid function is chosen. Thus, the probability of a node being classified as positive is:
The probability of being classified as negative is . Note that the formula includes , which is the vector corresponding to the non-leaf node.
For the four binary classifications experienced from the root node to the leaf node “football”, writing out the probabilities of each classification gives:
-
First classification: -
Second classification: -
Third classification: -
Fourth classification:
However, we want , that is “football”, what is its relationship with this probability? The relationship is:
Thus, through the small example of =”football”, the basic idea of Hierarchical Softmax has been introduced. In summary: for any word in the vocabulary, there must be a unique path from the root node to the leaf node corresponding to the word , and this path is unique. There are branches along the path, treating each branch as a binary classification, each classification generates a probability, and multiplying these probabilities gives the required .
The general formula for conditional probability can be written as:
where:
or expressed as an overall expression:
Substituting formula (8) into formula (6) yields:
For convenience in gradient derivation, we can simplify the double summation symbol under the formula to , that is:
Thus, the objective function formula (9) for the CBOW model has been derived, and next, we will discuss how to optimize it, that is, how to maximize this function. In Word2Vec, stochastic gradient ascent is used. The key to gradient-based algorithms is to provide the corresponding gradient calculation formulas for backpropagation.
4.1.3 Parameter Update
First, consider the gradient calculation with respect to :
Thus, the update formula for can be written as:
Next, consider the gradient with respect to :
At this point, we have calculated the gradient for , but what we actually want is the gradient for each word in , while is the result accumulated from all words in , so how can we use to update each word in ? The original authors chose a simple and straightforward method, directly using the gradient of to update :
4.2 Hierarchical Softmax for Skip-gram
This subsection introduces another model in Word2Vec – the Skip-gram model. Since the derivation process is quite similar to that of the CBOW model, we will directly start from the objective function and use the previously introduced notations.
4.2.1 Skip-gram Model Network Structure
The following figure shows the network structure of the Skip-gram model, which, like the CBOW model, consists of three layers: input layer, projection layer, and output layer. Below is a brief explanation of these three layers using the sample :
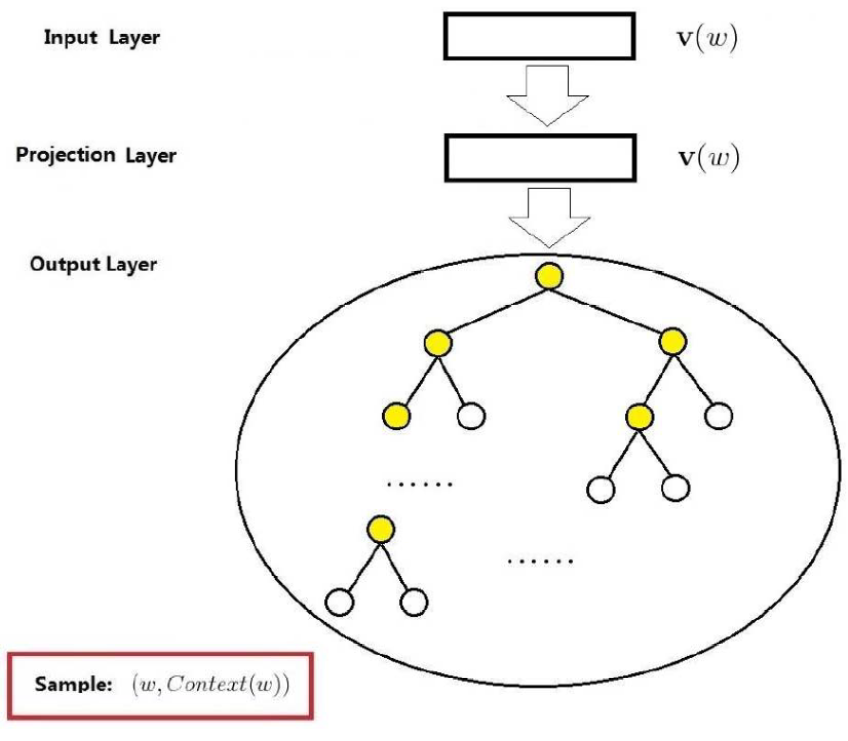
-
The input layer contains only the word vector of the current sample. -
The projection layer performs an identity projection, projecting to . Therefore, this projection layer is actually redundant; it is retained here mainly for comparison with the network structure of the CBOW model. -
The output layer, like the CBOW model, is also a Huffman tree.
4.2.2 Objective Function of Skip-gram
For the Skip-gram model, given the current word , it is necessary to predict the words in its context , so the objective function should be in the form of formula (7), and the key is the construction of the conditional probability function , which is defined in the Skip-gram model as:
The above formula can be written as:
Substituting formula (10) back in, we obtain the specific expression of the log-likelihood function formula (7):
Similarly, for convenience in gradient derivation, we will denote the content under the triple summation symbol as , that is:
Thus, the objective function for the Skip-gram model has been derived (formula 11), and we will also optimize it using stochastic gradient ascent. The key to gradient-based algorithms is to provide the corresponding gradient calculation formulas for backpropagation.
4.2.3 Parameter Update
First, consider the gradient calculation with respect to :
Thus, the update formula for can be written as:
Similarly, based on symmetry, we can easily obtain the gradient of with respect to :
We can also obtain the update formula for :
5. Model Based on Negative Sampling
This section will introduce the CBOW and Skip-gram models based on Negative Sampling. Negative Sampling (abbreviated as NEG) was proposed by Tomas Mikolov et al. in the paper “Distributed Representations of Words and Phrases and their Compositionality”. It is a simplified version of NCE (Noise Contrastive Estimation) aimed at improving training speed and enhancing the quality of the resulting word vectors. Compared to Hierarchical Softmax, NEG does not use a complex Huffman tree, but utilizes relatively simple random negative sampling, significantly improving performance, thus serving as an alternative to Hierarchical Softmax.
The details of NCE are somewhat complex; its essence is to use a known probability density function to estimate an unknown probability density function. Simply put, suppose the unknown probability density function is X, and the known probability density function is Y. If the relationship between X and Y is known, then X can also be determined. For specific details, please refer to the paper “Noise-contrastive estimation of unnormalized statistical models, with applications to natural image statistics”.
5.1 Brief Introduction to Negative Sampling Algorithm
As the name implies, negative sampling is a crucial aspect of the CBOW and Skip-gram models based on Negative Sampling. For a given word, how is it generated?
Words in the vocabulary appear with varying frequencies in the corpus; for high-frequency words, the probability of being selected as a negative sample should be relatively high, while for low-frequency words, the probability should be relatively low. This is our general requirement for the sampling process, which is essentially a weighted sampling problem.
Next, let’s help readers understand the mechanism of weighted sampling through a simple description. Suppose each word in the vocabulary corresponds to a line segment of length , where:
Here represents the number of times a word appears in the corpus (the summation term in the denominator is for normalization). Now, connect these line segments end to end to form a unit line segment of length . If a point is randomly placed on this unit line segment, the longer the segment (corresponding to high-frequency words), the greater the probability of being hit.
Now, let’s discuss the specific approach in Word2Vec. Let , where represents the th word in the vocabulary. Using as the splitting point, we can obtain a non-uniform partition on the interval , resulting in non-uniform partition intervals. We further introduce an equidistant partition on the interval , with partition points being , where , as shown in the illustration below.
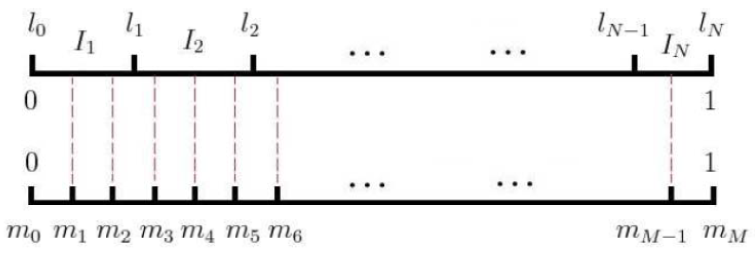
Figure: Illustration of the mapping establishment
With this mapping, sampling becomes simple: each time a random integer is generated within the range , that is a sample. Of course, there is also a detail: when performing negative sampling for , if by chance it is selected itself, what to do? Just skip it; this is also how the Word2Vec code handles it.
It is worth mentioning that when setting weights for words in the vocabulary in the Word2Vec source code, it is not done directly, but raised to the power of , where , thus transforming formula (12) into:
Additionally, in the source code, is set, which is the variable in the source code. The mapping formula (13) is completed by a function called InitUnigramTable.
5.2 CBOW Based on Negative Sampling
Having introduced the negative sampling algorithm, let’s derive the objective function for CBOW based on Negative Sampling. First, we select a negative sample subset regarding , for , we define the label of the word :
The above formula represents the label for the word , where the label for positive samples is , and for negative samples is .
For a given positive sample , the objective function we wish to maximize is:
where:
Here still represents the sum of the word vectors in , and serves as an auxiliary vector for the parameters to be trained.
Why maximize ? Let’s take a look at the expression and substitute formula (15) into formula (14):
Here, represents the probability of predicting the center word given the context , and represents the probability of predicting the center word given the context , which can be seen as a binary classification problem. Formally, maximizing is equivalent to maximizing while minimizing all . Isn’t this what we want? Increase the probability of positive samples while reducing the probability of negative samples. Thus, for a given corpus, we can construct the function:
as the final overall optimization objective. Of course, for convenience in derivation, we take the logarithm, and the final objective function becomes:
Similarly, for convenience in derivation, we take :
Next, we use stochastic gradient ascent to calculate the gradient. First, consider the gradient with respect to :
Then the update formula for can be written as:
Similarly, based on symmetry, we can derive the gradient for :
Then the update formula for can be written as:
5.3 Skip-gram Based on Negative Sampling
This subsection introduces the Skip-gram model based on Negative Sampling. The idea is the same as that of the CBOW model introduced in the previous section, so we will directly start from the objective function and use the previously introduced notations.
For a given sample , we wish to maximize:
where:
or expressed as an overall expression:
Here represents the negative sample subset generated when processing the word . Thus, for a given corpus, the function:
can serve as the overall optimization objective. Similarly, we take the logarithm, and the final objective function becomes:
For convenience in gradient derivation, we still extract the content under the triple summation symbol, denoting it as , that is:
Next, we use stochastic gradient ascent to calculate the gradient. First, consider the gradient with respect to :
Then we obtain the update formula for :
6. Thoughts on Several Issues Regarding Word2Vec
(1) What are the principles of the two algorithm models of Word2Vec, and how to draw the network structure?
(2) What are the inputs and outputs of the network? What is the activation function of the hidden layer? What is the activation function of the output layer?
(3) What is the objective function/loss function?
(4) How does Word2Vec obtain word vectors?
(5) Derive how the parameters of Word2Vec are updated?
(6) Which model of Word2Vec performs better and which is faster? Why?
(7) What methods are there to speed up training for Word2Vec?
(8) Introduce Negative Sampling, what impact does it have on low-frequency and high-frequency words? Why?
(9) What are the differences and connections between Word2Vec and Latent Dirichlet Allocation (LDA)?
The above questions can be answered through this article and referenced articles, and will not be detailed here.
(10) Introduce the computation process of Hierarchical Softmax, how is Huffman integrated into the network? How are parameters updated? What impact does it have on low-frequency and high-frequency words? Why?
Hierarchical Softmax utilizes the Huffman tree based on word frequency to build the tree, where nodes with high word frequency are closer to the root node, and low-frequency nodes are farther away. Thus, during training, the parameters along the path of low-frequency words can receive more training, resulting in better performance.
(11) What parameters does Word2Vec have, and are there any tuning suggestions?
-
The speed of Skip-Gram is slightly slower than CBOW, but it performs better on low frequencies in small datasets; -
Sub-Sampling Frequent Words can improve both the speed and accuracy of the algorithm, with a suggested sample value of ; -
Hierarchical Softmax is more friendly to low-frequency words; -
Negative Sampling is more friendly to high-frequency words; -
The dimensionality of vectors is generally better when higher, but not absolute; -
Window Size: Skip-Gram is generally around 10, while CBOW is around 5.
(12) What limitations does Word2Vec have?
As a simple and easy-to-use algorithm, Word2Vec also has many limitations:
-
Word2Vec only considers contextual information while ignoring global information; -
Word2Vec only considers the co-occurrence of contexts while ignoring their order;
7. Applications of Word2Vec in Industry
The main principle of Word2Vec is to predict words based on context, as the meaning of a word can often be extracted from the sentences before and after it.
User behavior is also a similar time series that can be inferred through context. When users browse and interact with content, we can infer the abstract features of their behavior from their interactions, which allows us to apply word vector models to recommendation and advertising fields.
7.1 In the NLP Field
-
The word vectors learned by Word2Vec represent the semantics of words and can be used for classification, clustering, and calculating word similarity. -
The vectors generated by Word2Vec can be directly used as inputs to deep neural networks for tasks such as sentiment analysis.
7.2 Graph Embedding
There are many Graph Embedding methods based on Word2Vec, which can be referenced in papers like DeepWalk (a classic graph embedding algorithm that introduces Word2Vec ideas), node2vec, struc2vec, etc.
7.3 In the Recommendation Field
-
Airbnb proposed in the paper “Real-time Personalization using Embeddings for Search Ranking at Airbnb” to compose a list of user browsing behavior and learn item vectors using Word2Vec, resulting in a 21% increase in click-through rates and driving 99% of booking conversion rates. This paper mainly improved upon the Skip-gram model.
-
Yahoo proposed in the paper “E-commerce in Your Inbox: Product Recommendations at Scale” to extract products from shopping receipts sent to users and compose a list, learning and recommending potential products to users using Word2Vec;
7.4 In the Advertising Field
Yahoo proposed in the paper “Scalable Semantic Matching of Queries to Ads in Sponsored Search Advertising” to compose a list of user search queries and ads, learning feature vectors for them to match suitable ads for given search queries.
8. Reference
[1] Rong X. word2vec parameter learning explained[J]. arXiv preprint arXiv:1411.2738, 2014.[2][Paper] Word2Vec: A Silver Bullet for Word Embedding, address: https://mp.weixin.qq.com/s/7dsjfcOfm9uPheJrmB0Ghw [3] Detailed Explanation of Word2Vec – Formula Derivation and Code – link-web article – Zhihu https://zhuanlan.zhihu.com/p/86445394 [4] The Illustrated Word2Vec, Jay Alammar, address: https://jalammar.github.io/illustrated-word2vec/ [5] Illustrated Word2Vec (Original Translation), address: https://mp.weixin.qq.com/s/Yq_-1eS9UuiUBhNNAIxC-Q [6] What are the advantages of Word2Vec over previous Word Embedding methods? – Zhihu https://www.zhihu.com/question/53011711 [7][NLP] Understand the essence of word vectors Word2Vec in seconds – Mu Wen’s article – Zhihu https://zhuanlan.zhihu.com/p/26306795 [8] http://mccormickml.com/2016/04/19/word2vec-tutorial-the-skip-gram-model/ [9] In-depth analysis of the word2vec model – TianMin’s article – Zhihu https://zhuanlan.zhihu.com/p/85998950 [10] A Neural Probabilistic Language Model – Zhang Jun’s article – Zhihu https://zhuanlan.zhihu.com/p/21240807 [11] What applications does word2vec have? – Zhihu https://www.zhihu.com/question/25269336
Finally, in addition to the cited literature, I also recommend some materials I have read: [1] “Deep Learning Word2Vec Learning Notes”, Beiliu Wandering Son. [2] “Mathematics in Word2Vec”, peghoty. [3] “Deep Learning Practical Word2Vec”, NetEase Youdao.
This article mainly refers to peghoty’s “Mathematics in Word2Vec”, which is very well written, strongly recommended for everyone to learn. In addition, I have organized high-quality materials collected during my learning of Word2Vec, reply with [Word2Vec] in the public account to receive.

