
Artificial neural networks are actually like a complex calculator; you input something, and it gives you a result. Just like when you input 2+2 into a calculator, it outputs 4, but an artificial neural network can handle not just simple arithmetic; it can process more complex things like images, text, etc. So, when we say that an artificial neural network is a function approximator, we mean that it can simulate various complex computational processes, helping us get the desired output from the input.

If it’s a picture of a car, there must be a function that can take this picture and predict what type of car it is, just from the raw pixel values.

For traditional programming, if there is a piece of English text, there must be a function that can take this text and output the same text, but in Chinese.

If you have a question, there must be a function that can generate an answer.
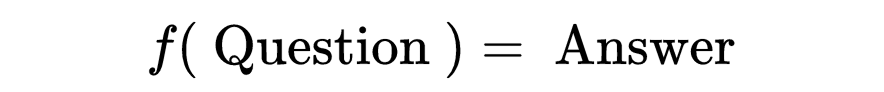
But the problem is, in traditional programming, we have been writing functions that are very powerful, but what happens when the functions become so complex that we cannot explain them? For example, when you see this number,

You know it is 5, but if you had to write an algorithm that takes this image and says it is 5, suddenly it becomes extremely difficult.
The task is simple, but writing a function that takes an image of a handwritten digit and outputs which digit it is, is very difficult. So this is why we need machine learning. The idea here is simple: if you know there exists a function that can solve this problem, but we do not know what that function looks like, perhaps we can define a structure, an artificial neural network, that can learn this function, and to learn this function, it needs something to learn from, which means it needs data, like many different images of handwritten digits.
Let’s look at a very simple example,
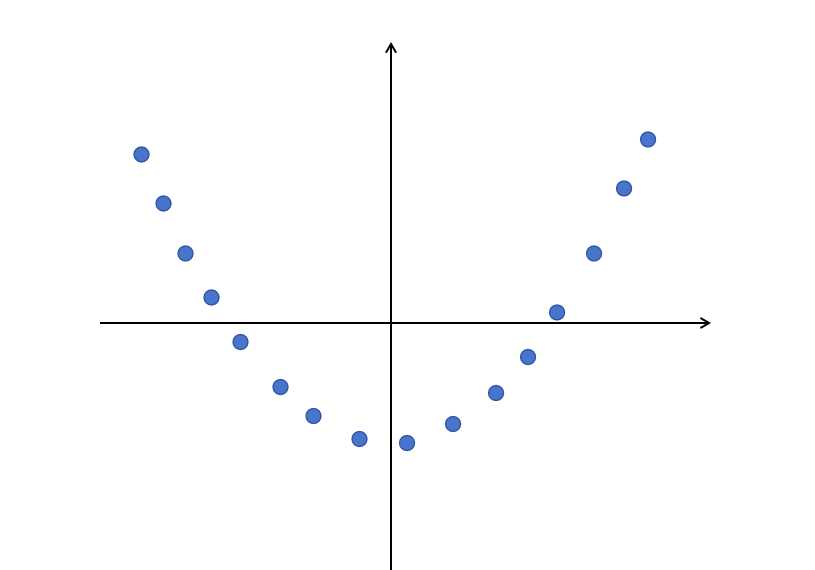
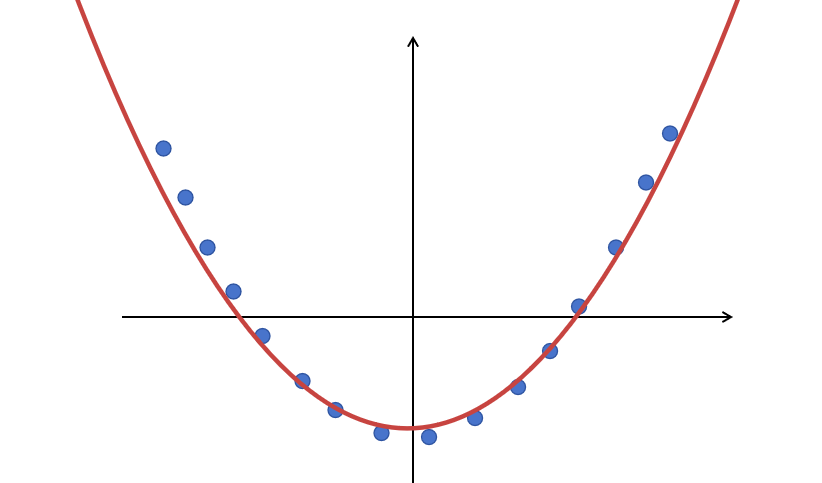
You can see some data points; if I ask you what function simulates these data, you might imagine a curve passing through these data points. This is what the neural network should also learn; it should learn to approximate the function represented by these data. If a new x value appears, we should be able to predict the y value, even if we did not know this point before.
Back to handwritten digits, a very famous handwritten digit dataset called MNIST, which contains thousands of handwritten digits.

If you want to create a model that learns from this data to recognize unseen handwritten digits, you can draw inspiration from how the human brain learns.
Our brain consists of many cells called neurons. Neurons have parts like antennas called dendrites, which are used to receive signals from other neurons. The body of the neuron decides whether to pass these signals to the next neuron. If it decides to pass them, the neuron sends the signals through a long line called an axon until the signal reaches another place called a synapse. At the synapse, the signal is passed to the next neuron. This is how our brain processes and transmits information at a basic level.
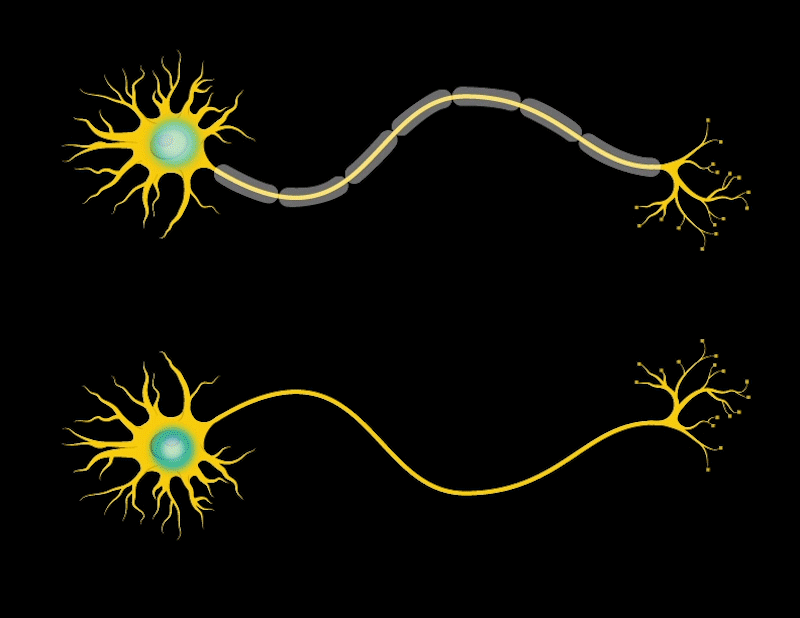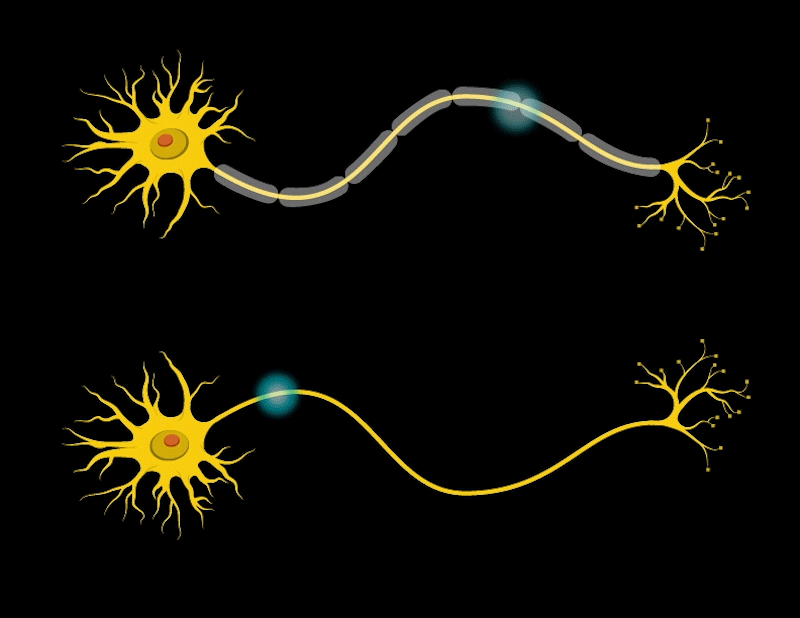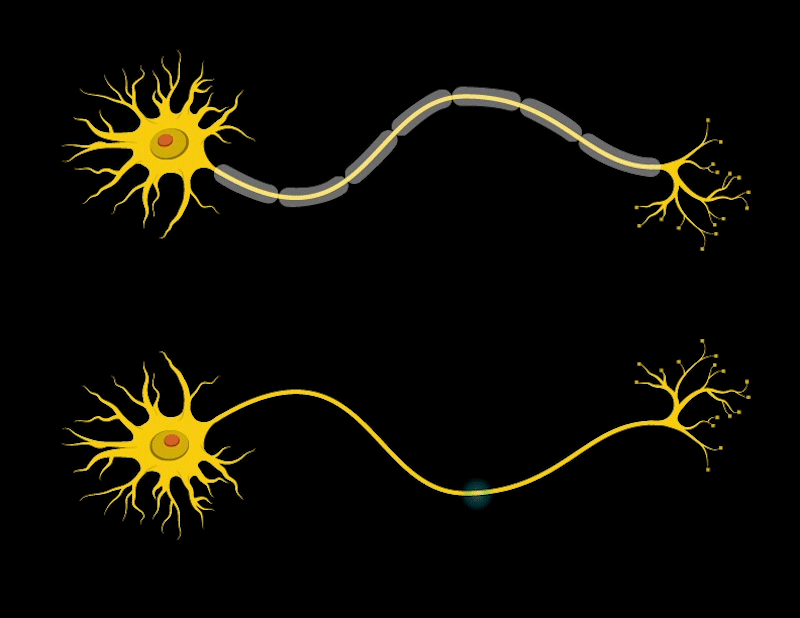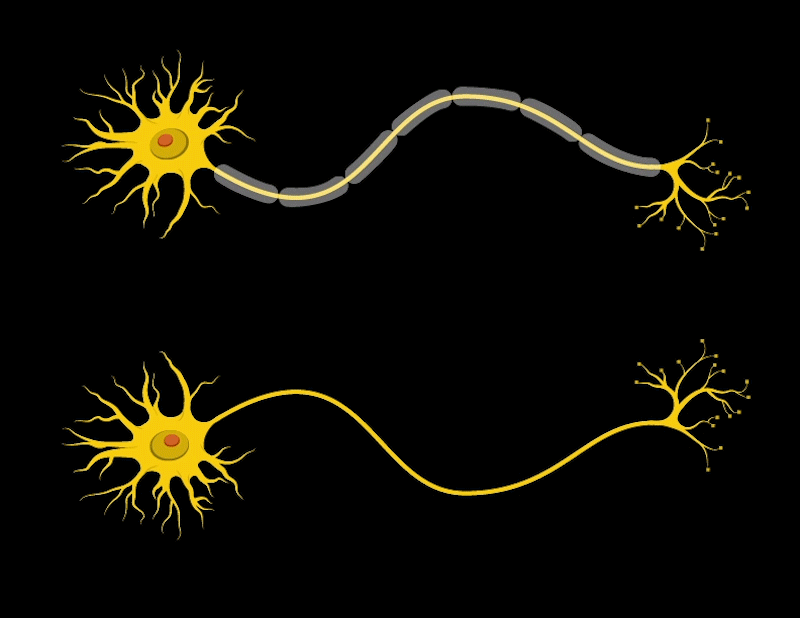
When we learn, the connections between neurons in the brain change; they become stronger, forming new connections, and neurons become more efficient.

Artificial neural networks attempt to simulate this process; they consist of artificial neurons, which are simple functions that receive values from other neurons and combine them into a signal to be passed to other neurons.

In this specific case, the image above is a 28×28 pixel image, where each pixel value ranges from 0 to 1, with black pixels being 0 and white pixels being 1. These pixels form the input layer.
Now we want to know which digit the image displays, as there are 10 possible digits, we produce 10 predictions for each input image, so we can add 10 neurons here and call them the output layer.

Each input neuron (a pixel) will connect to each output neuron (the 10 digits from 0 to 9), and we connect them with what we call weights. Each weight is just a number, which can be randomly chosen at the beginning.
In this example, there are 784 input neurons (corresponding to the 28×28 pixel image), and each input neuron is connected to 10 output neurons (corresponding to the 10 possible digits). So there will be a total of 784 pixels multiplied by 10 digits, which is 7840 connections. Each connection has a weight, which will be adjusted during the training process so that the network can correctly identify the digit in the input image.
Each output neuron will take the input values, multiply each value by the corresponding weight, and sum them to get a new value,
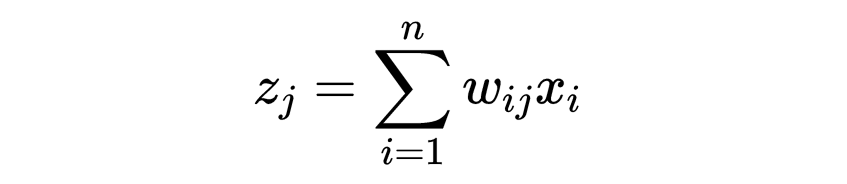
In this case, we expect the neuron representing the digit 5 to give a high value (weight), while the values given by neurons representing other digits should be lower. This way, the network can correctly identify that the input image is the digit 5.
If the input digit is 0, once again, only the output neuron representing 0 should light up (receive a high value), this might be the simplest neural network we can construct.
But our task is to teach this artificial neural network to recognize these digits, which means we must somehow change the weights to make the model make better predictions. This is done by showing the network a series of sample images (like images of handwritten digits) and then observing whether the network’s predictions are accurate. If the network’s predictions are inaccurate, the weights need to be adjusted.
To know how to adjust the weights, we use a tool called loss function, which helps us measure the difference between the network’s predictions and the actual results. Our goal is to make this loss as small as possible, meaning our predictions are more accurate.

In fact, if you visualize the weights of each neuron, as the model learns, we can see that although they initially look random, as the model learns and trains, these weights gradually adjust and begin to form specific patterns. These patterns allow the model to recognize the features of different digits, thus distinguishing them. Initially, the model may only learn simple linear relationships, meaning it can distinguish some very basic digit features.
To allow the model to learn more complex relationships, we can add more layers between the input layer and the output layer; these additional layers are called hidden layers.

Adding more hidden layers can make the neural network “deeper”, which is the concept of “deep learning.” The neurons in the hidden layers work similarly to those in the output layer, but each neuron also has an activation function, which can be non-linear, allowing the model to learn more complex relationships and thus improving the accuracy of digit recognition.
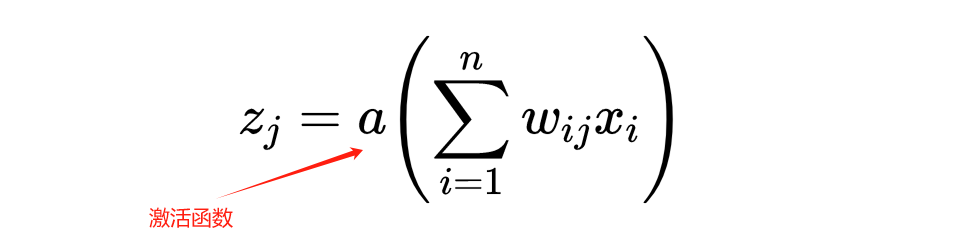
Going back to the simple two-dimensional function example, the activation function will allow us to bend the line so that we can more accurately simulate the data.
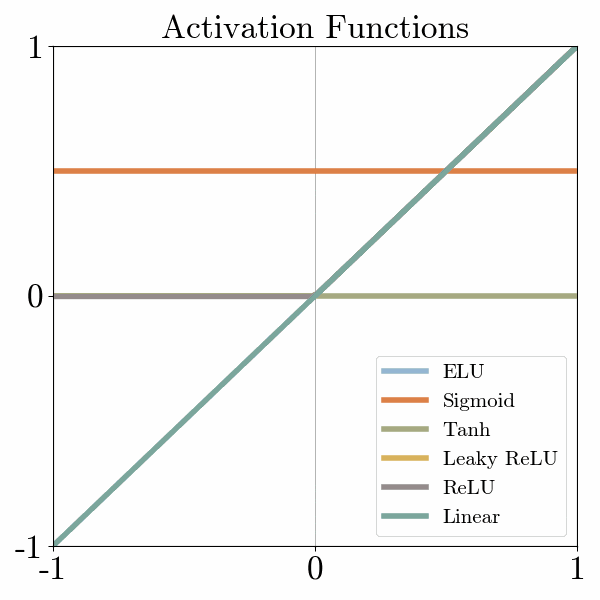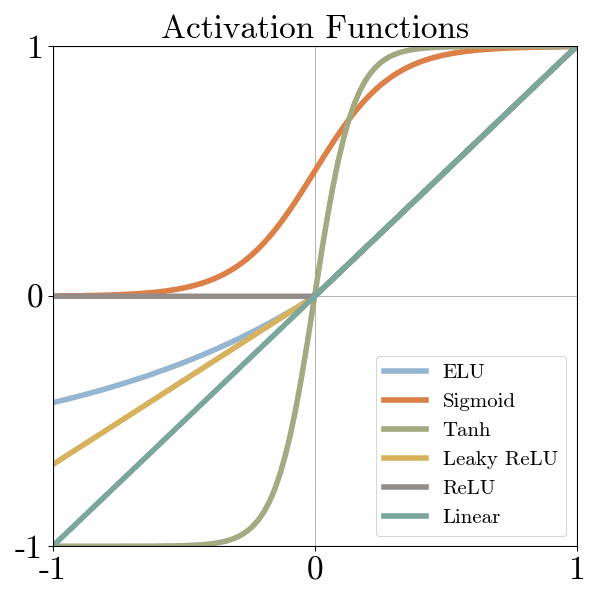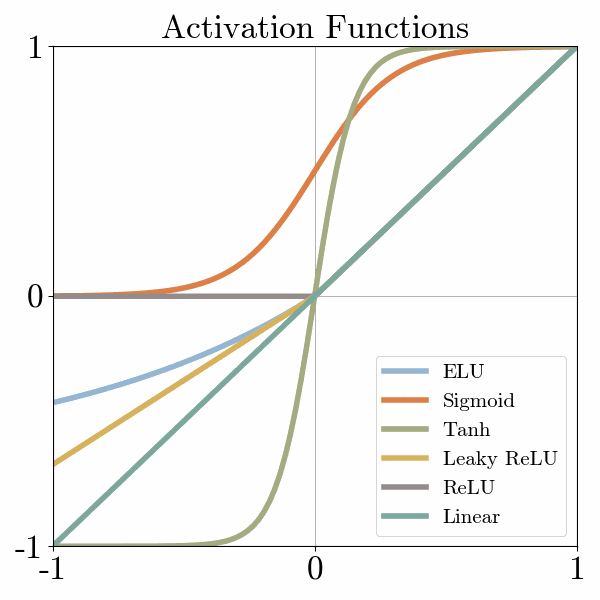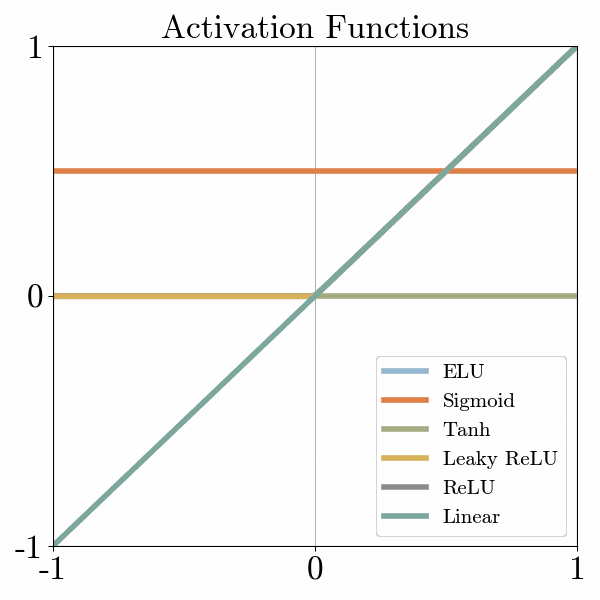
There are many activation functions, but one of the simplest is called ReLu, which turns negative numbers to 0 and keeps positive numbers unchanged.
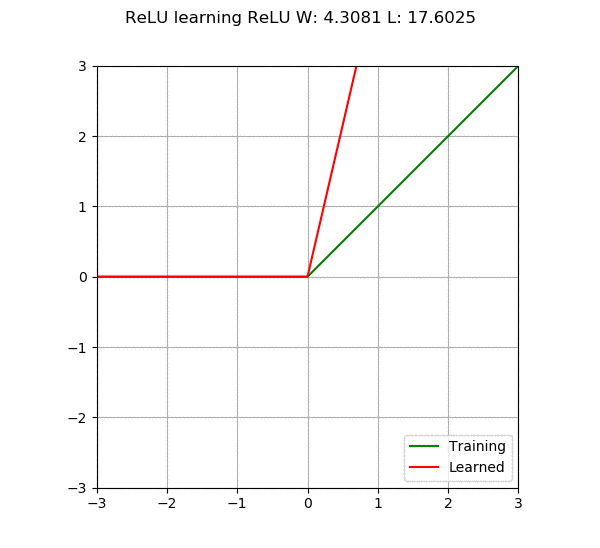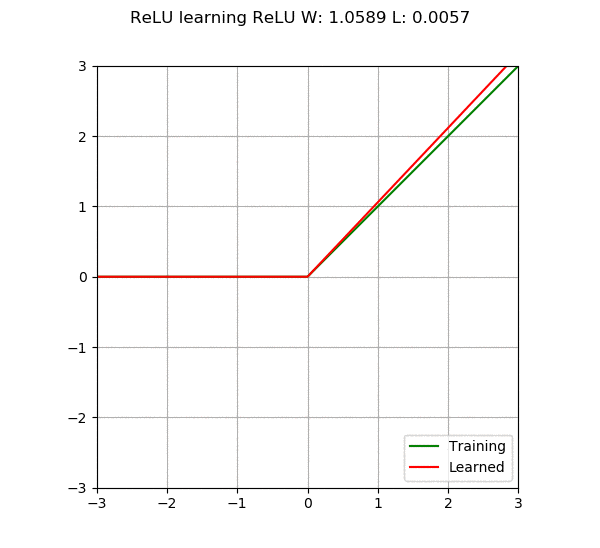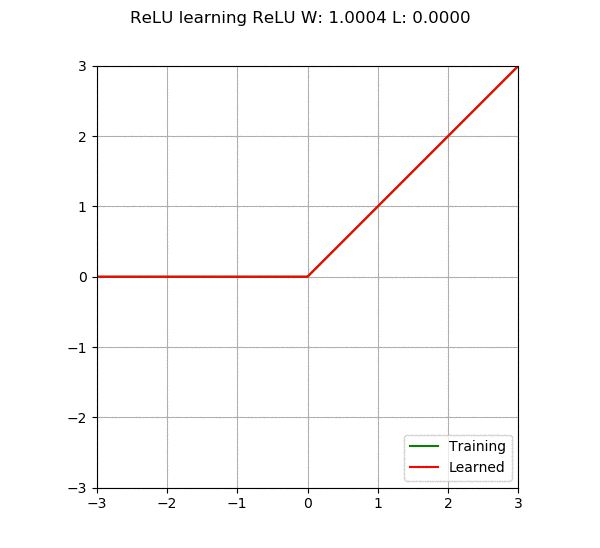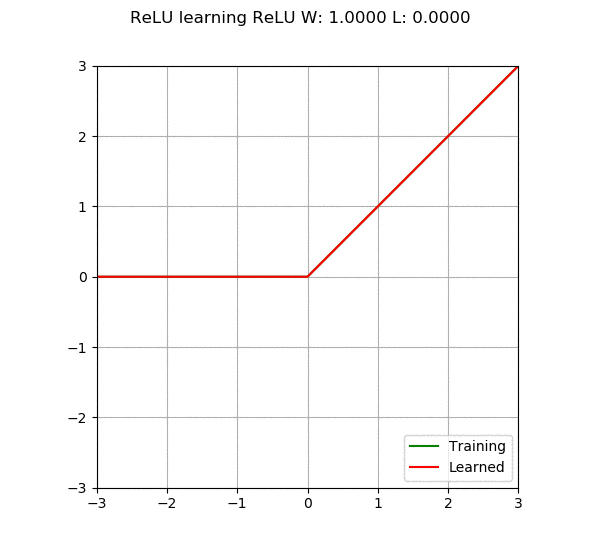
When we add more neurons or layers to the neural network, its capability increases, meaning it can learn more complex things. However, there is a problem; if we make the network too large, it may become too “smart” to not only learn what we want it to learn but also remember all the training data. This situation is called overfitting, which is like the model becoming too focused on the training data, resulting in poor performance when faced with new, unseen data. On the other hand, if the model is too simple, it may not learn enough, which is called underfitting. Therefore, the main goal of a neural network is to find a balance, constructing a model that is neither too complex nor too simple, capable of learning patterns from the data.
