This article is the fourth in the Illustrated Transformer series. In the first three articles, we learned about the detailed architecture and working principles of the Transformer, as well as the operation mechanism of multi-head attention. In the last article, we will delve deeper into the internal workings of the attention module, exploring why the attention mechanism is effective and the detailed calculation principles of the attention mechanism.
1. Illustrated Transformer – Function Overview: Explains how to use the Transformer, why the Transformer outperforms RNNs, as well as the architecture of the Transformer and its operation during training and inference.
2. Illustrated Transformer – Layer-by-Layer Introduction: Explains how the Transformer operates, elucidating the internal operational mechanism of the Transformer from the perspective of data dimension changes or matrix transformations, in an end-to-end manner.
3. Illustrated Transformer – Multi-Head Attention: Explains the multi-head attention mechanism, detailing how the attention mechanism works throughout the Transformer.
The attention module (Attention module) exists in each Encoder and Decoder. Amplifying the encoder’s attention:
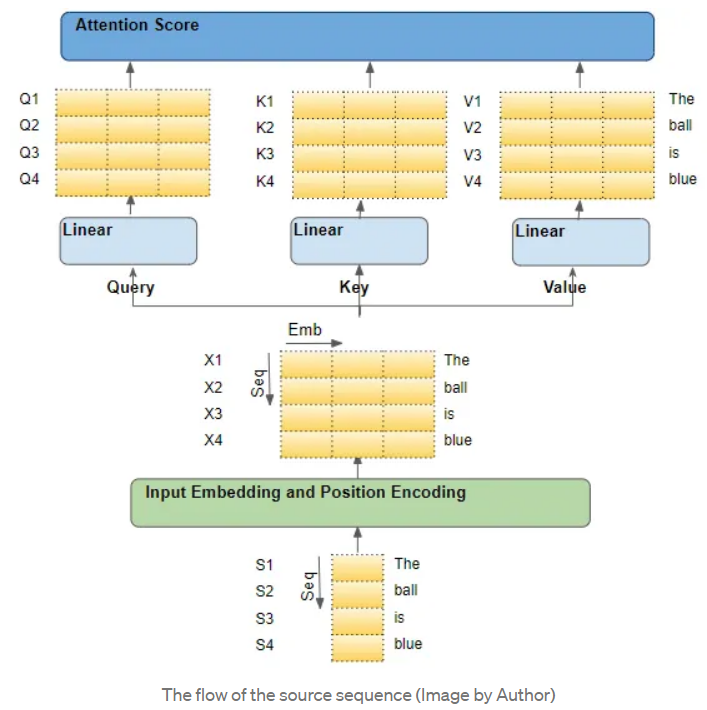
For example, let’s assume we are dealing with an English-to-Spanish translation problem, where one sample’s source sequence is “The ball is blue“, and the target sequence is “La bola es azul“.
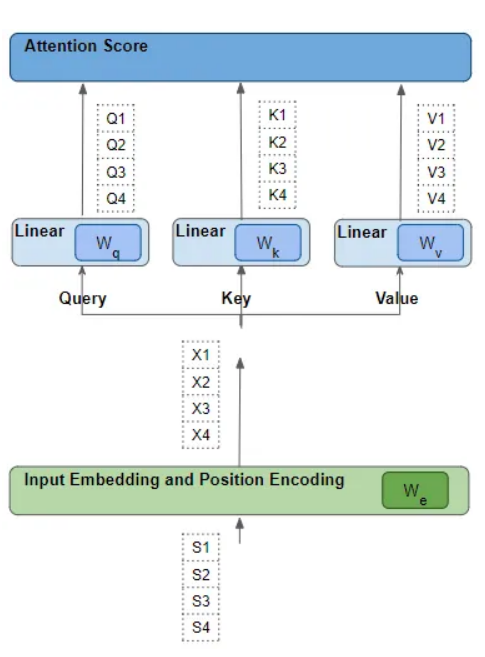
The source sequence first passes through the Embedding and Position Encoding layers, generating embeddings for each word in the sequence. The embeddings are then passed to the encoder, reaching the Attention module.
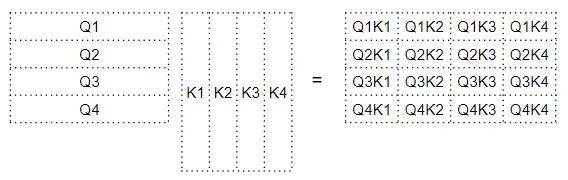
Within the Attention module, the embedded sequence goes through three linear layers (Linear layers), producing three independent matrices—Query, Key, and Value. These three matrices are used to calculate attention scores.Each “row” of these matrices corresponds to a word in the source sequence.
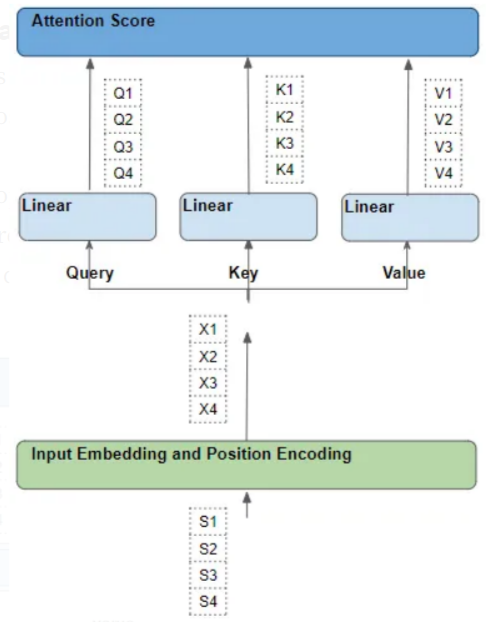
2. Each row entering the attention module corresponds to a word in the original sequence
One way to understand Attention is to start from a single word in the source sequence and observe its path within the Transformer. By focusing on the Attention module, we can clearly see how each word interacts with others.
Therefore, special attention must be paid to the operations performed by the Attention module on each word, and how each vector maps to the original input word, without worrying about details such as matrix shapes, specific calculations, or how many attention heads there are, as these details do not directly relate to the fate of each word.
To simplify explanation and visualization, let’s ignore the embedding dimensions and consider one “row” as a whole.
3. Each row undergoes a series of learnable transformation operations
The key question is, how does the Transformer determine which set of weights will yield the best results? Remember this question; we will return to it later.
4. How to obtain attention scores
Within the Attention module, multiple steps are executed, and here we focus only on the linear layers and the “attention” scores (Attention Score).
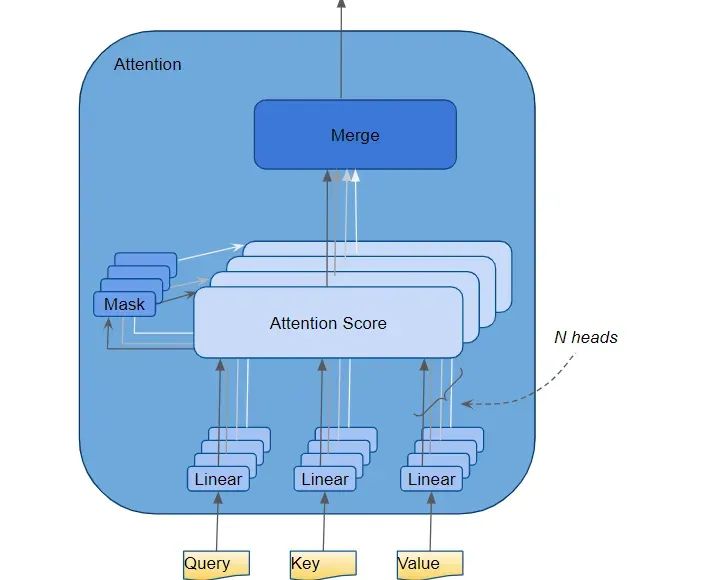
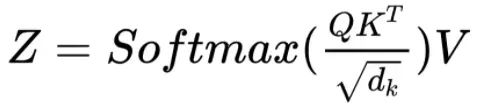
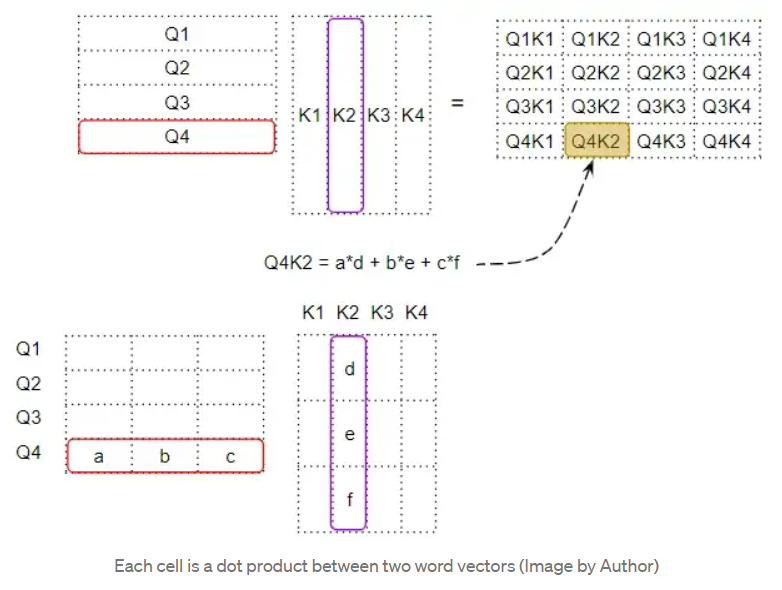
From the formulas, we can see that the first step in the Attention module involves performing a dot product operation between the Query matrix and the transposed Key matrix. Let’s see what happens to each word.
Query is dot-multiplied with the transposed Key to produce an intermediate matrix known as the “factor matrix“. Each cell of the factor matrix corresponds to the matrix multiplication between two word vectors.
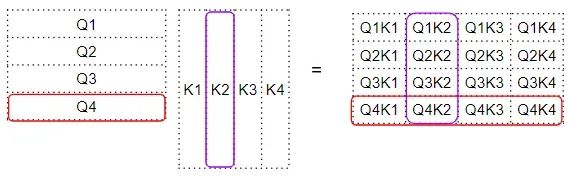
The factor matrix is then multiplied with the V matrix to produce the attention scores (Attention Score). We can see that the 4th row of the output matrix corresponds to the multiplication of the Q4 matrix with all corresponding K and V:
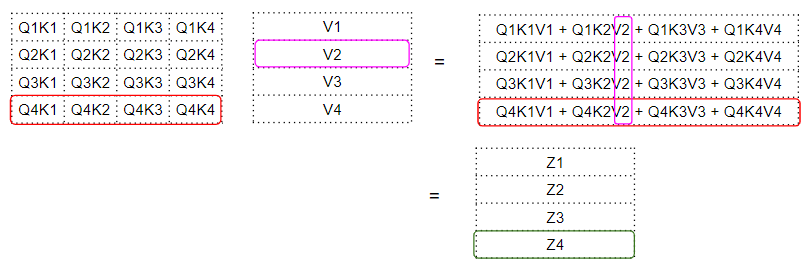
This produces the attention score vector output by the attention module—Attention Score vector (Z).
The attention score can be understood as an “encoding value” of a word. This encoding value is weighted by the “factor matrix” against the words in the Value matrix. The corresponding weights in the “factor matrix” are the dot products of the Query vector and Key vectors of that specific word. To reiterate:

5. The role of Query, Key, and Value
For a specific query vector Query, it can be understood as the word for which we are calculating the attention score. The Key vector and Value vector are the words we are observing, i.e., the degree of relevance of that word to the query word.
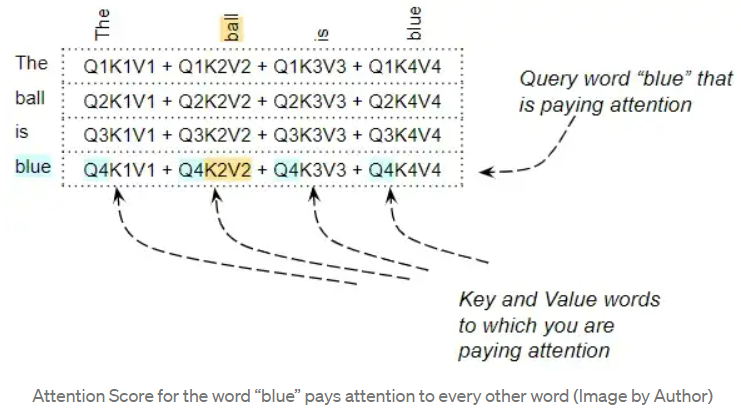
For instance, in the sentence “The ball is blue”, the row for the word “blue” contains the attention scores of “blue” with every other word. Here, “blue” is the Query word, while the others are the “Key/Value”.
The calculation of attention also involves other operations, such as division and Softmax calculations, but these can be ignored in this article. They merely alter the values in the matrix without affecting the positions of each word row in the matrix. They also do not involve any interactions between words.
6. Dot Product: Measuring Similarity Between Vectors
Attention Score is obtained by performing dot multiplication and then summing them up to capture the relationship between a specific word and other words in the sentence. But how does matrix multiplication help the Transformer determine the relevance between two words?
To understand this, remember that the Query, Key, and Value rows are actually vectors with embedding dimensions. Let’s zoom in to see how the matrix multiplication between these vectors is calculated:
When we perform a dot product between two vectors, we multiply pairs of numbers and then sum them up:
-
If both paired numbers (like ‘a’ and ‘d’ above) are either both positive or both negative, the product will be positive, contributing to the final sum.
-
If one number is positive and the other is negative, the product will be negative, reducing the final sum.
-
If the product is positive, the larger the two numbers, the greater their contribution to the final sum.
This means that if the signs of the corresponding numbers in the two vectors are consistent, the final sum will be larger.
The concept of dot product mentioned above also applies to the calculation of the Attention score. If the vectors of two words are more aligned, the Attention score will be higher. We expect the Transformer to operate such that for two words in a sentence, if they are related, their Attention score will be high, while for two unrelated words, we expect their score to be low.
For example, in the sentence “The black cat drank the milk”, the word “milk” is very relevant to “drank”, less so to “cat”, and not at all to “black”. We hope that “milk” and “drank” will yield a high attention score, while “milk” and “cat” will yield a somewhat lower score, and “milk” and “black” will yield a negligible score. This is the output we hope the model learns to produce.
To achieve this, the word vectors for “milk” and “drank” must be consistent. The vectors for “milk” and “cat” will diverge somewhat, while those for “milk” and “black” will differ significantly.
Let’s return to the previous question—how does the Transformer find out which set of weights will yield the best results?
The word vectors are generated based on the word embeddings and the weights of the linear layers. Hence, the Transformer can learn these embedding vectors, linear layer weights, etc., to produce the desired word vectors mentioned above.
In other words, it will learn these embeddings and weights in such a way that:
If two words in a sentence are related, their word vectors will be aligned, resulting in a higher attention score; for words that are unrelated, the word vectors will not align, resulting in a lower attention score.
Thus, the embeddings for “milk” and “drank” will be very consistent, yielding a higher attention score. For “milk” and “cat”, they will diverge somewhat, yielding a slightly lower score, while for “milk” and “black”, they will differ significantly, resulting in a very low score.
This is the principle of the attention module.
The dot product between Query and Key calculates the relevance between each pair of words. This relevance is then used as a “factor” to compute the weighted sum of all Value vectors. The output of this weighted sum is the attention score.
The Transformer learns to make related words more consistent through the learning of embedding vectors.
This is one of the reasons for introducing three linear layers: to provide more parameters for the Attention module to adjust word vectors through learning.
There are three instances of the attention mechanism used in the Transformer:
1. Self-attention mechanism in the Encoder: Attention calculation of the source sequence with itself;
2. Self-attention mechanism in the Decoder: Attention calculation of the target sequence with itself;
3. Attention mechanism in Encoder-Decoder: Attention calculation of the target sequence against the original sequence.
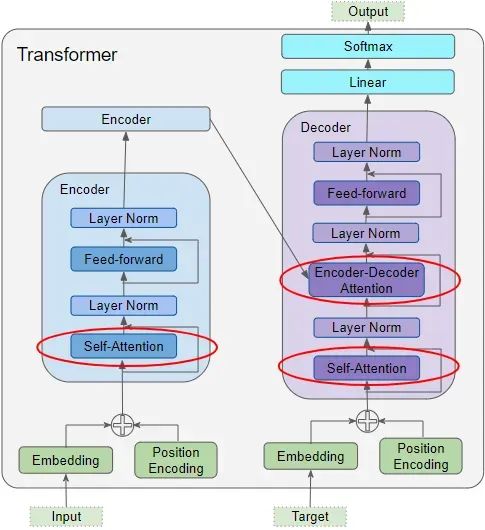
In “Encoder Self Attention“, we calculate the relevance of each word in the source sequence with other words in the source sequence. This occurs in all Encoders in the encoder stack.
Most of what is seen in Encoder Self Attention also applies to Decoder Self Attention, with only minor but important differences.
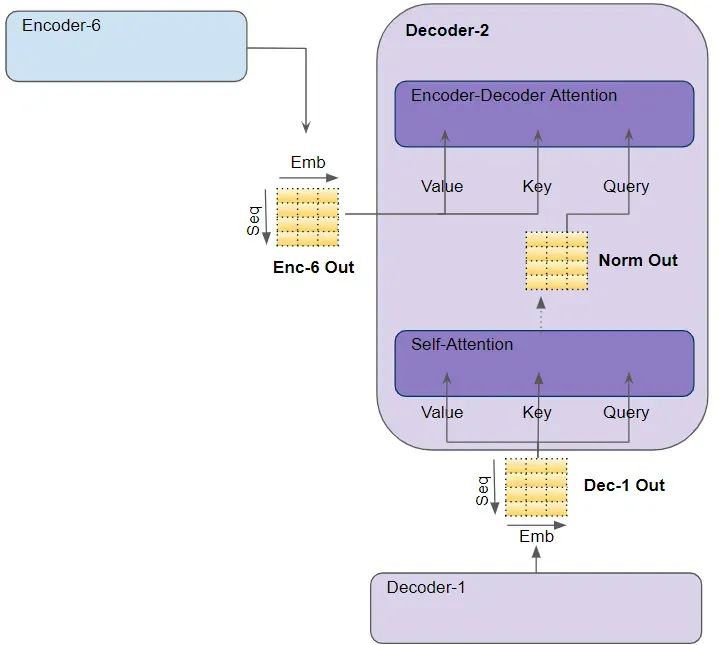
In Decoder Self Attention, we calculate the relevance of each word in the target sequence with other words in the target sequence.
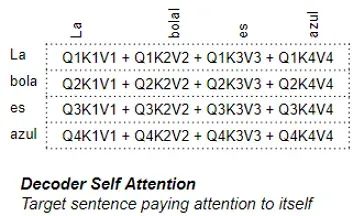
In “Encoder-Decoder Attention“, the Query comes from the target sentence while the Key/Value comes from the source sentence. This way, it can calculate the relevance of each word in the target sentence with each word in the source sentence.
I hope these four translations allow you to appreciate the elegance of the Transformer design and deeply understand its principles. I would also like to sincerely thank the original author Ketan Doshi for his creativity and spirit of sharing.
In the future, I will seek more technical illustration topics for writing or foreign translations. If you have questions about data analysis, machine learning, deep learning, etc., please leave a message on the public account, and I will choose suitable topics to explain using illustrations.
Original article link:
https://towardsdatascience.com/transformers-explained-visually-not-just-how-but-why-they-work-so-well-d840bd61a9d3