Overview of Transformer Privacy Inference Technology

1. Introduction

The Transformer model, especially large language models (LLMs) based on Transformers, has made significant progress in the field of artificial intelligence in recent years. The emergence of applications such as ChatGPT and Bing has made the capabilities of these models known and utilized by the public. These models effectively capture long-term dependencies in input sequences using attention mechanisms, allowing them to accurately model contextual information. Unlike traditional task-specific learning methods, large Transformer models (such as GPT and BERT) are trained on vast amounts of unlabeled text data and can be directly applied to various applications such as sentiment analysis, language translation, content generation, and question answering.

However, the application of large Transformer models also brings some risks, particularly privacy issues. Most Transformer models operate as machine learning as a service (MLaaS), where servers provide models and inference services to users. In this model, users need to transmit data to the company’s servers and cannot directly control how their data is used. This raises concerns about data privacy among users, leading some countries, such as Italy, to temporarily ban the use of ChatGPT.

Private Transformer Inference (PTI) technology aims to address privacy issues during the inference process of Transformer models. PTI is an encryption protocol that allows model inference to occur without the server knowing the user’s input and the user knowing the server’s model. In recent years, private inference of Transformers has been achieved using secure Multi-Party Computation (MPC) and Homomorphic Encryption (HE) technologies. MPC enables multiple parties to compute functions on their inputs without revealing their respective inputs. HE allows computations to be performed on encrypted data without decryption, enabling data to be processed in encrypted form, thereby protecting privacy and security throughout the computation process.

Based on the paper “A Survey on Private Transformer Inference” by researchers at Nanyang Technological University, this article reviews the latest research findings using various private computation technologies to implement PTI, focusing primarily on MPC and HE technologies. The article discusses their advantages and disadvantages and proposes some future research directions.

2. Background

2.1 Definition of Private Inference

Assume that client C has private data x, and server S hosts model M. Client C wants to use model M to compute inference results M(x). The privacy requirement is that the server knows nothing about x, and the client knows nothing about M except for the information that can be inferred from M(x). The formal definition is as follows:

Definition 1. The protocol Π between server S (which has model M) and client C (which has input x) is considered private if it satisfies:

• Correctness. The final output of protocol Π (denoted as y) is the same as the correct inference result M(x).

• Security. Here, we introduce the concept of a simulator (Sim) to define the security of the protocol. A simulator is a hypothetical algorithm that simulates the behavior of one party during the execution of the protocol.

• Compromised Client. Even if client C is compromised, there exists a valid simulator SimC such that , where denotes the view of the compromised C during the execution of protocol Π, meaning that the adversary cannot obtain more information from executing the protocol than from the simulator.
• Compromised Server. Even if server S is compromised, there exists a valid simulator SimS such that , where denotes the view of the compromised S during the execution of protocol Π.

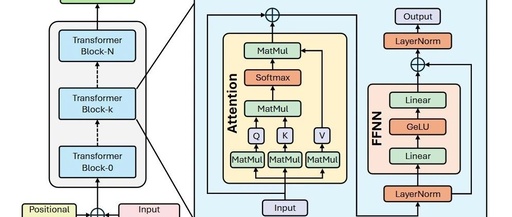
2.2 Transformer Architecture

The Transformer is an encoder-decoder architecture where both parts have similar structures. Here, we primarily focus on the encoder part. The encoder consists of a stack of identical blocks, each containing two sub-layers: a multi-head self-attention mechanism and a feed-forward network. Each sub-layer uses residual connections and layer normalization (LayerNorm). The architecture and flowchart of the encoder are shown in Figure 1.

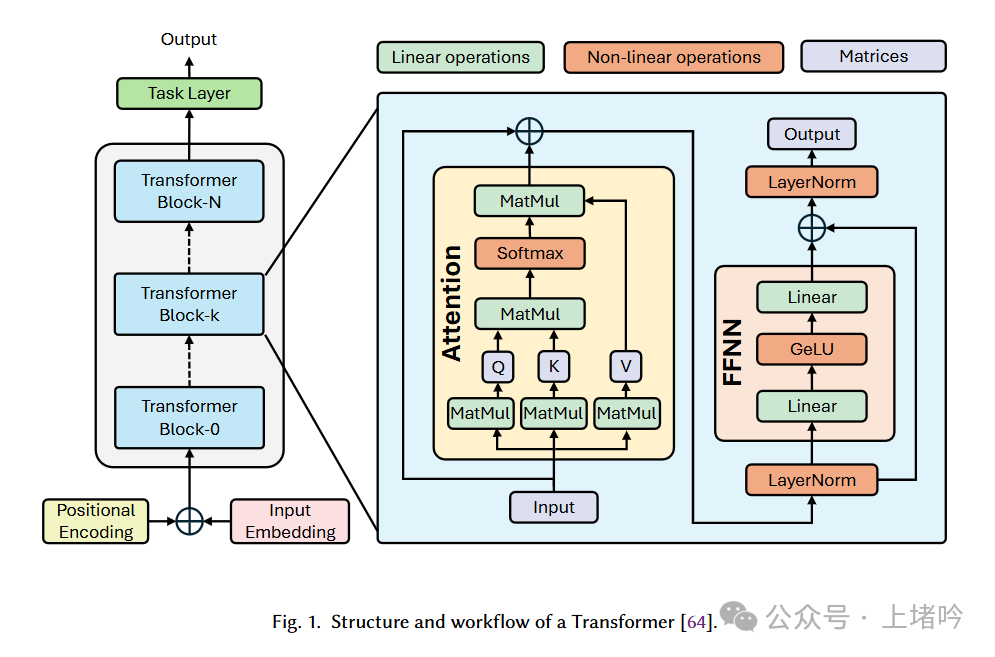
• Embedding Layer: Converts each word in the input sequence into the corresponding word vector. Word vectors are dense vector representations that capture the semantic information of words. The embedding layer typically uses pre-trained word vector models, such as Word2Vec or GloVe.
• Multi-Head Attention Layer: The attention mechanism allows the model to focus on other words in the input sequence while processing each word. The multi-head attention mechanism computes multiple attention scores in parallel and concatenates the results to capture information from different subspaces.
• Scaled Dot-Product Attention: The core of the attention calculation, which measures the relevance between words by calculating the dot product between query vectors, key vectors, and value vectors. To avoid the vanishing gradient problem, the dot product result is divided by the square root of the dimension of the query and key vectors.
• Multi-Head Attention: Divides the input into multiple heads, each performing Scaled Dot-Product Attention independently, and then concatenates the results. Each head can learn different attention patterns, capturing richer semantic information.
• Feed-Forward Layer: Comprises two linear transformations and a non-linear activation function to further extract features from the output of the attention layer. The linear transformations map the input vectors to a higher-dimensional space, while the non-linear activation function introduces non-linearity, enhancing the model’s expressive power.
• Layer Normalization: Normalizes the feature vectors of each word, accelerating model training and improving performance. Layer normalization normalizes the mean and variance of each feature vector to 0 and 1, avoiding the vanishing and exploding gradient problems.
• Residual Connection: Adds the input and output of each sub-layer, helping to alleviate the vanishing gradient problem. Residual connections allow gradients to flow directly to the lower layers, accelerating model training.

2.3 Privacy Protection Technologies

This section introduces common encryption technologies involved in current PTI research.

2.3.1 Functional Encryption

Functional Encryption (FE) is an encryption technology that allows specific function computations on encrypted data. Unlike traditional encryption schemes, FE not only hides the data itself but also conceals the specific content of the computation function. Users can encrypt data with a key and then send the encrypted data and function key to the server. The server can compute on the encrypted data using the function key but cannot obtain any other information about the original data and function. The advantage of FE lies in its ability to achieve fine-grained access control, but its disadvantage is relatively low efficiency and currently only supports a limited type of functions. For example, FE can be used for image recognition tasks, where users can send encrypted images to the server, which can recognize the encrypted images using the FE key but cannot obtain any other information about the images.

2.3.2 Secure Multi-Party Computation (MPC)

Secure Multi-Party Computation (MPC) is an encryption technology that allows multiple parties to collaboratively execute computational tasks without revealing their respective inputs. MPC protocols typically involve multiple participants, each owning their private input. The participants compute by exchanging encrypted information, ultimately obtaining the computation result, but no party can gain information about the inputs of others. Common MPC techniques include:

• Secret Sharing: Divides a secret into multiple shares, distributing them to different participants. The original secret can only be recovered when enough participants cooperate. For example, a secret can be split into two shares, each sent to two participants. Each participant holds their share and cannot learn any information about the original secret. Only when both participants cooperate can they combine their shares to recover the original secret.
• Oblivious Transfer: The sender possesses multiple messages, and the receiver can choose to receive one of the messages, but the sender does not know which message the receiver chose, nor can the receiver obtain any information about the other messages. For example, an online store can use oblivious transfer to send product information to users. Users can choose to receive information about products they are interested in, but the store does not know which products the users chose, nor can the users obtain information about other products.
• Garbled Circuits: Represents the computational task as a Boolean circuit, then encrypts and obscures the circuit so that the participants can compute without revealing their inputs. For example, two participants can use garbled circuits to compare their respective secret numbers without revealing the actual numbers.

2.3.3 Homomorphic Encryption (HE)

Homomorphic Encryption (HE) is an encryption technology that allows direct computations on encrypted data. The computation result remains encrypted, and decrypting it yields the same result as performing the same operation on unencrypted data. The main types of HE include:

• Partially Homomorphic Encryption (PHE): Supports homomorphic computation for only one operation, such as addition or multiplication. For example, the RSA encryption algorithm supports multiplicative homomorphism and can be used for multiplication operations on encrypted data.
• Somewhat Homomorphic Encryption (SHE): Supports a limited number of addition and multiplication operations. For example, the Brakerski-Gentry-Vaikuntanathan (BGV) encryption scheme supports a limited number of addition and multiplication operations and can be used to compute simple polynomial functions.
• Fully Homomorphic Encryption (FHE): Supports arbitrary numbers of addition and multiplication operations. For example, the Gentry encryption scheme was the first to implement FHE and can be used to compute any complex function.
• Leveled Fully Homomorphic Encryption (LFHE): Supports computations of any circuit within a predefined depth. For example, the Fan-Vercauteren (FV) encryption scheme is an LFHE scheme that can compute circuits of limited depth.

3. Privacy Threats in Secure Inference

In private inference, two main privacy threat models are considered:

• Semi-honest Model: Assumes that all parties involved in the computation will honestly comply with the protocol but will attempt to collect additional privacy information during execution. For example, the server may try to infer the user’s input information from the encrypted data, or the client may attempt to obtain information about the model’s parameters. The semi-honest model is an idealized model suited for scenarios where there is some level of trust between parties.
• Honest-Majority Model: Assumes that as long as the majority of participants are honest and comply with the protocol, it can prevent a minority of dishonest participants from tampering with the process or stealing private information. For example, in a 3PC setup, as long as at least two participants are honest, the security of the computation can be guaranteed. The honest-majority model is suited for scenarios where there is no complete trust between parties.

4. Overview of Private Transformer Inference Research: Setup, Encryption Methods, Advantages and Disadvantages

4.1 Bottlenecks of Private Transformer Inference

In recent years, significant advancements have been made in private inference technologies for traditional CNN and RNN models. However, due to the structural differences of Transformer models, private Transformer inference presents new challenges:

• Large Matrix Multiplication: Transformer models involve a large amount of matrix multiplication, unlike the matrix-vector multiplication widely studied in CNNs. This greatly increases both computational and communication overhead. For example, the attention mechanism of the BERT model involves a significant number of matrix multiplication operations, which are inefficient in the encrypted domain.
• Complex Non-linear Functions: Transformer models widely use complex non-linear functions such as GeLU, Softmax, and LayerNorm. These functions are not very friendly to encryption primitives, leading to lower efficiency. For instance, the computation of the GeLU function involves the error function, which is challenging to implement efficiently in the encrypted domain.

4.2 Overview of PTI Research and Adopted Encryption Technologies

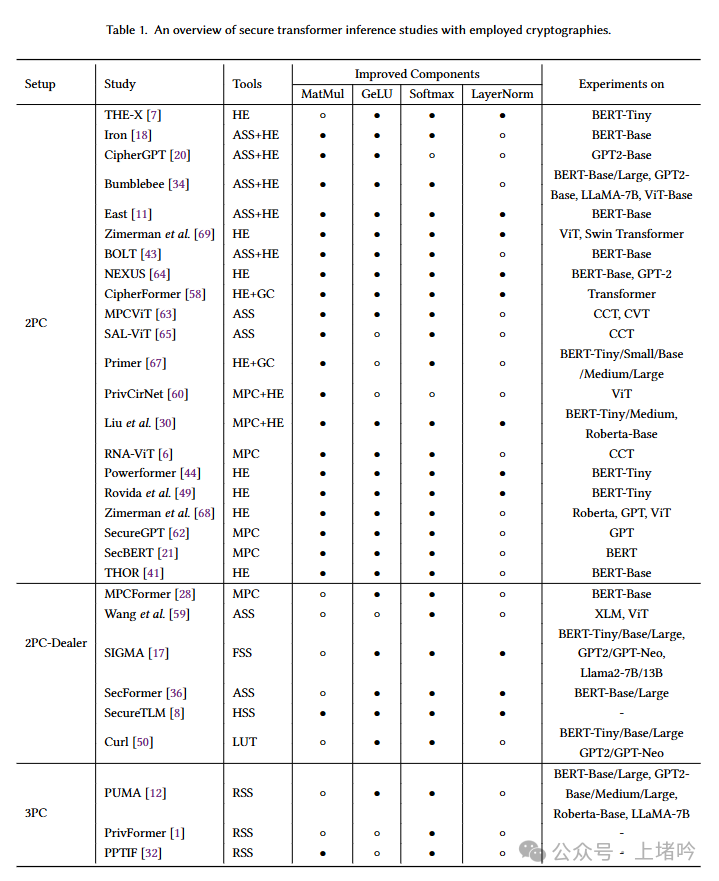
In recent years, numerous research findings have emerged in the field of PTI, primarily focusing on how to utilize MPC and HE technologies to achieve private inference for Transformer models. Different studies have adopted various MPC setups and HE schemes and have made some optimizations based on the structural characteristics of Transformer models. The table below lists some representative PTI studies and briefly introduces their characteristics.

• 2PC Setup: Many studies have adopted a 2PC setup, where only two parties participate in the computation. The advantage of this setup is its simplicity, but the disadvantage is relatively low efficiency.
• 2PC-Dealer Setup: Some studies have adopted a 2PC-Dealer setup, introducing a trusted third party to generate preprocessed data. This setup can improve efficiency but requires additional trust assumptions.
• 3PC Setup: A few studies have adopted a 3PC setup, where three parties participate in the computation. This setup can further improve efficiency and security but requires more communication overhead.

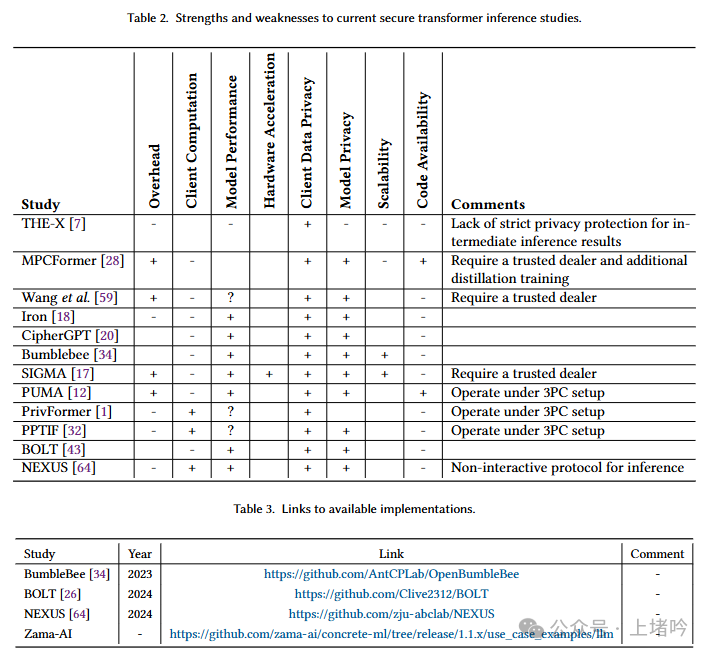
4.3 Advantages and Disadvantages of Existing Research

• Client Computation: Some schemes require significant computation on the client side, which may pose a challenge for resource-constrained devices. For example, some HE-based schemes require the client to perform operations on ciphertext, which may be too time-consuming for mobile devices.
• Model Performance: Due to the overhead of encrypted computation, the performance of PTI schemes is generally lower than plaintext inference. For example, some MPC-based schemes require extensive communication, which increases inference latency.
• Code Availability: Many studies do not provide open-source code, limiting their application and promotion. For example, some studies only provide experimental results without detailed implementation specifics.

5. Linear Layers in Transformers

Linear layers in Transformers mainly involve large matrix multiplication (MatMul) in the attention mechanism and feed-forward layer. This section discusses the latest research findings on secure MatMul in PTI.

5.1 Large Matrix Multiplication

Inference with Transformer models may involve hundreds of large matrix multiplications. The design of efficient and secure MatMul protocols is crucial for PTI research. Existing secure MatMul protocols can be categorized into two types:

• Secret Sharing-Based Schemes: Each element of the matrix is secret shared among multiple parties, and computations are performed using the properties of secret sharing. For example, two parties can hold two secret shares of a matrix and compute the matrix product by exchanging encrypted information without revealing the original matrix.
• Homomorphic Encryption-Based Schemes: The matrix is encrypted, and computations are performed using the properties of HE. For example, the matrix can be encrypted and sent to the server, which can use HE to perform multiplication on the encrypted matrix and then return the encrypted result to the client.

5.2 Secret Sharing-Based MatMul Protocols

Secret sharing schemes support local addition operations, so the key is how to effectively implement multiplication while protecting privacy. Some studies utilize HE to assist in multiplication operations within secret sharing schemes, such as:

• 2PC+HE Scheme: Two parties hold secret shares of the matrix and perform multiplication operations using HE, finally decrypting and combining the results. This scheme can leverage the efficient multiplication operations of HE to accelerate computations but requires additional communication to exchange HE ciphertexts.
• 2PC-Dealer and 3PC Schemes: Utilize a trusted dealer or third party to generate multiplication triples, enabling efficient multiplication operations. Multiplication triples consist of three random numbers that satisfy a * b = c. Participants can use multiplication triples to compute the product of secret shares without performing HE operations.

5.3 Homomorphic Encryption-Based MatMul Protocols

Research on using HE for matrix multiplication in Transformers is still relatively scarce. Matrix multiplication is compatible with HE since it only involves addition and multiplication, but direct implementation may be inefficient. Some studies propose optimization methods such as:

• Reducing Transmission Overhead: Utilizing HE packing techniques to pack multiple plaintext data into a single ciphertext, thereby reducing the number of communications. For example, multiple elements of a matrix can be packed into one ciphertext and processed in a single HE operation instead of performing HE operations on each element separately.
• Reducing Computational Overhead: Using more efficient HE schemes, such as the CKKS scheme, or leveraging hardware acceleration for computation. The CKKS scheme is an HE scheme that supports floating-point operations, enabling more efficient matrix multiplication. GPUs can parallel process a large number of HE operations, accelerating computations.
• Overcoming Multiplication Depth Limits: Using leveled HE schemes or decomposing matrix multiplication into multiple smaller multiplication operations. Leveled HE schemes can support deeper HE operations, enabling more complex calculations. Decomposing matrix multiplication into multiple smaller operations can reduce the depth of HE operations, improving efficiency.

6. Non-linear Layers

Due to the complexity of non-linear functions in Transformer models within encryption primitives, ensuring the security of these functions is another challenge.

6.1 Softmax

A key challenge in the attention mechanism is how to efficiently implement the Softmax operation. The Softmax function involves exponentiation and division operations, which are inefficient in the encrypted domain. Some studies propose the following optimization methods:

• Using More Encryption-Friendly Functions: For example, using the ReLU function or its variants to approximate the Softmax function. The ReLU function is a piecewise linear function that is easier to implement in the encrypted domain.
• Polynomial Approximation: Using low-degree polynomials to approximate the Softmax function, thereby reducing computational complexity. Polynomial functions only involve addition and multiplication, making them easier to implement in the encrypted domain.
• Lookup Tables: Pre-computing the values of the Softmax function and storing them in a lookup table to reduce online computational load. Lookup tables can convert complex function calculations into simple lookup operations, improving efficiency.

6.2 GeLU

Transformer models use the GeLU activation function instead of the encryption-friendly ReLU. The computation of the GeLU function involves the error function, which is inefficient in the encrypted domain. Some studies propose the following optimization methods:

• Using ReLU or Its Approximations: For example, using the ReLU function or its piecewise linear approximation to replace the GeLU function. The ReLU function is a piecewise linear function that is easier to implement in the encrypted domain.
• Lookup Tables: Pre-computing the values of the GeLU function and storing them in a lookup table. Lookup tables can convert complex function calculations into simple lookup operations, improving efficiency.
• Polynomial Approximation: Using low-degree polynomials to approximate the GeLU function. Polynomial functions only involve addition and multiplication, making them easier to implement in the encrypted domain.

6.3 Layer Normalization

Layer normalization ensures that the inputs to different layers of the network have consistent means and variances, aiding in stabilizing deep neural networks. The computation of layer normalization involves square root and division operations, which are inefficient in the encrypted domain. Some studies propose the following optimization methods:

• Simplifying Parameter Computation: For example, using fixed parameters or pre-computing parameters to reduce online computational load.
• Custom Protocols: Designing secure computation protocols specifically for layer normalization, such as utilizing a combination of secret sharing and HE for efficient computation.
• Lookup Tables: Pre-computing the values of the layer normalization function and storing them in a lookup table. Lookup tables can convert complex function calculations into simple lookup operations, improving efficiency.

7. Evaluation Report

This section compares the experimental results provided in selected studies and analyzes the performance of different schemes.

7.1 Models and Datasets

The Transformer models and datasets used to evaluate PTI performance are crucial to the comparative results. The structure and scale of the models affect the efficiency of PTI schemes, while the scale and difficulty of the datasets affect the accuracy of the models. Commonly used models include:

• BERT: A pre-trained model for natural language understanding tasks. BERT models come in various variants, such as:

  Different BERT variants achieve varying balances between performance and efficiency.

• <span>BERT-Tiny</span>: A very small parameter variant of BERT with only 4.4M parameters, suitable for resource-constrained devices.
• <span>BERT-Base</span>: Contains 12 encoder layers, a hidden layer dimension of 768, and 12 attention heads, with a parameter scale of 110M.
• <span>BERT-Large</span>: Contains 24 encoder layers, a hidden layer dimension of 1024, and 16 attention heads, with a parameter scale of 340M.

• GPT: A pre-trained model for natural language generation tasks. GPT models also have various variants, such as:

  The variants of GPT primarily differ in terms of the number of layers, hidden layer dimensions, and the number of attention heads, all of which affect model performance and efficiency.

• <span>GPT2-Base</span>: Contains 12 decoder layers, a hidden layer dimension of 768, and 12 attention heads, with a parameter scale of 117M.
• <span>GPT2-Medium</span>: Contains 24 decoder layers, a hidden layer dimension of 1024, and 16 attention heads, with a parameter scale of 345M.
• <span>GPT-Neo</span>: Similar to the GPT-2 architecture but utilizes different training data and optimization methods.

• ViT: A Transformer model for image classification tasks. The ViT model segments images into multiple small patches and processes each patch as a word in the input sequence. For example, <span>ViT-Base</span> contains 12 encoder layers, a hidden layer dimension of 768, and 12 attention heads, with a parameter scale of 86M. The ViT model performs comparably to CNN models but with higher parallelism.

• LLaMA: A large language model released by Meta. The LLaMA model has a parameter scale of up to 7 billion, exhibiting strong language understanding and generation capabilities. For example, <span>LLaMA-7B</span> contains 32 decoder layers, a hidden layer dimension of 4096, and 32 attention heads. The performance of the LLaMA model surpasses that of GPT-3 but with a smaller parameter scale.

Commonly used datasets include:

• GLUE: A benchmark dataset for natural language understanding tasks. GLUE includes several different natural language understanding tasks, such as:

  GLUE benchmark tests can comprehensively evaluate a model’s natural language understanding capabilities.

• Single-Sentence Tasks: CoLA (grammaticality judgment), SST-2 (sentiment classification)
• Similarity and Paraphrase Tasks: MRPC (sentence semantic equivalence judgment), STS-B (semantic textual similarity), QQP (question semantic equivalence judgment)
• Inference Tasks: MNLI (natural language inference), QNLI (question natural language inference), RTE (text entailment recognition), WNLI (Winograd natural language inference)

• Wikitext-103: A dataset for language modeling tasks. Wikitext-103 contains a large amount of text data from Wikipedia, which can be used for training and evaluating language models.

• ImageNet: A dataset for image classification tasks. ImageNet contains millions of labeled images, which can be used for training and evaluating image classification models.

7.2 Evaluation Metrics

Metrics for evaluating PTI performance include:

• Accuracy: Measures the accuracy of model inference. Accuracy is typically calculated as the proportion of correctly predicted samples to the total number of samples. In the GLUE benchmark, accuracy is a primary evaluation metric.
• Runtime: Measures the time required for model inference. Runtime is typically measured in milliseconds or seconds required to complete one inference. The runtime of PTI schemes is generally longer than that of plaintext inference due to the need for additional encrypted computations and communications.
• Communication Overhead: Measures the amount of data exchanged between parties. Communication overhead is typically measured in bytes or megabytes exchanged. The communication overhead of MPC protocols is generally larger than that of HE schemes because they require multiple rounds of interaction.
• Computational Overhead: Measures the resources required for participants to perform computations, such as CPU time and memory usage. The computational overhead of HE schemes is generally larger than that of MPC protocols because they involve complex ciphertext operations.

Analysis of Experimental Results

Different PTI studies utilize various models, datasets, and evaluation metrics, making it challenging to directly compare their performance. Overall, MPC-based schemes typically outperform HE-based schemes in terms of accuracy, but with greater runtime and communication overhead. In contrast, HE-based schemes have advantages in runtime and communication overhead but may have lower accuracy. Some studies have improved performance by optimizing MPC protocols or HE schemes, such as reducing the number of communication rounds or lowering the complexity of ciphertext operations.

8. Conclusion

This paper reviews the latest research findings in the field of private Transformer inference (PTI), focusing on the two main technical routes of secure multi-party computation (MPC) and homomorphic encryption (HE). The goal of PTI is to achieve the inference capabilities of Transformer models while protecting user data and model parameter privacy. Significant progress has been made in the PTI field in recent years, with various MPC and HE-based schemes proposed, addressing privacy protection issues during the inference process of Transformer models to varying degrees.

However, the development of PTI still faces several challenges. The structural characteristics of Transformer models, such as large matrix multiplication and complex non-linear functions, pose significant challenges to the efficiency of PTI schemes. Many studies focus on optimizing MPC protocols and HE schemes to enhance the efficiency of PTI, such as:

• Optimizing Matrix Multiplication: Achieving efficient matrix multiplication operations using secret sharing techniques, homomorphic encryption techniques, or a combination of both. Some studies leverage HE packing techniques and SIMD techniques to reduce communication and computational overhead.
• Approximating Non-linear Functions: Approximating non-linear functions such as Softmax, GeLU, and LayerNorm using polynomial approximations, lookup tables, or other encryption-friendly functions. Some studies also utilize the special properties of functions for optimization, such as the approximate linearity and symmetry of the GeLU function.

In addition to efficiency issues, PTI also needs to address security enhancements and practicality improvements. Future research directions include:

• Performance Enhancement: Further optimizing the computational efficiency of matrix multiplication and non-linear functions, for example, exploring more efficient HE schemes and MPC protocols, and leveraging hardware acceleration technologies such as GPUs and FPGAs.
• Security Enhancement: Designing PTI schemes that resist stronger attack models, such as considering malicious models and malicious clients, and preventing side-channel attacks and model extraction attacks.
• Practicality Improvement: Reducing the computational overhead on clients to make it suitable for resource-constrained devices, such as mobile devices and IoT devices. Additionally, support for more types of Transformer models, such as those used for image recognition, speech recognition, and video analysis, is needed, along with the development of user-friendly PTI tools and libraries to apply PTI technologies in practical scenarios.

In summary, PTI, as an emerging technology, has great potential in protecting user privacy and promoting AI applications. With continuous development and improvement of the technology, PTI will play an increasingly important role in the future.

Reference paper: arXiv:2412.08145v1 [cs.CR] 11 Dec 2024