How Neural Networks Learn to Predict

GPT is undoubtedly familiar to everyone. When we converse with it, we usually only focus on the questions we ask (inputs) and the answers provided by GPT (outputs). We have no idea how the output is generated; it is like a mysterious black box.

GPT is a natural language processing (NLP) model based on neural networks, trained using a large amount of data input into the neural network until the model’s output meets our expectations to some extent. A well-trained model can accept user input and provide answers after “thinking” based on the key information in the input. To understand how GPT “thinks,” we may start from neural networks.

2. What is a Neural Network?

So, what exactly is a neural network? Or rather, why neural networks?

High school biology tells us that the human nervous system consists of billions of interconnected neurons, which are biological cells with major structures such as cell bodies, dendrites, and axons. The dendrites and axons of different neurons connect with other neurons through synapses, forming a complex neural network in the human brain.

To enable machines to achieve intelligence close to that of humans, artificial intelligence attempts to mimic the thinking process of the human brain, creating a computational model that imitates the connections between neurons in the brain—neural networks. It consists of multiple layers of neurons, each receiving input and producing corresponding output. According to this definition, the internal structure of the black box in Figure 1 is beginning to take shape, where each circle in the diagram represents a neuron that has computational capabilities and can pass the computed results to the next neuron.

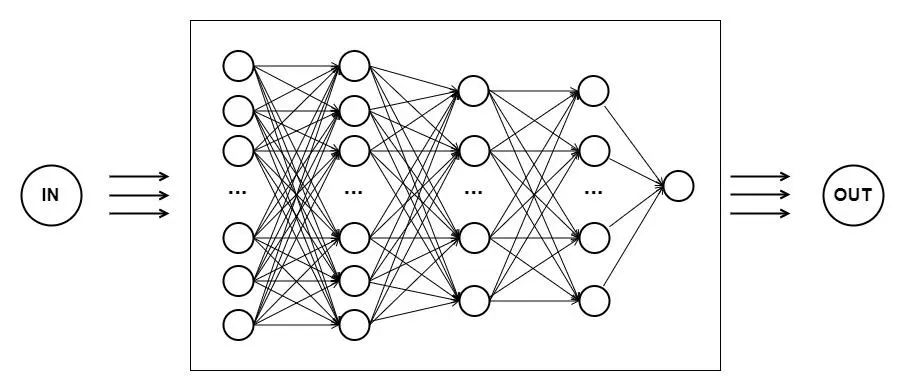
In biology, the simpler the structure of the brain, the lower the intelligence; correspondingly, the more complex the nervous system, the more problems it can handle, and the higher the intelligence. The same applies to artificial neural networks; the more complex the network structure, the more powerful the computational ability. This is why deep neural networks have been developed. They are called “deep” because they have multiple hidden layers (i.e., the number of vertical neuron layers in the above figure). Compared to traditional shallow neural networks, deep neural networks have more hierarchical structures.

The process of training deep neural networks is called deep learning. Once the deep neural network is constructed, we only need to input training data into the neural network, and it will spontaneously learn the features in the data. For example, if we want to train a deep neural network to recognize cats, we only need to input a large number of images of cats of different breeds, postures, and appearances for it to learn. Once training is successful, we can input any image into the neural network, and it will tell us whether there is a cat in it.

3. How Neural Networks Compute

Now that we know what a neural network is and its basic structure, how do the neurons in the neural network compute the input data?

Before that, we need to solve a problem: how is data input into the neural network? Let’s explain this with image and text data as examples.

How Data is Input into Neural Networks

1. Image Input Processing

Imagine a scene: when we enlarge an image to a certain extent, we can see small squares. These small squares are called pixels. The more pixels an image has, the higher the pixel density, and the clearer the image. Each pixel is made up of a single color, and the three primary colors in optics—red, green, and blue—can be mixed in different degrees to produce all other colors. In the RGB model, the intensity of each color can be represented by a numerical value, usually between 0 and 255. A red intensity value of 0 means no red light, while 255 means maximum red light intensity; the green and blue intensity values are similar.

To store an image, a computer must store three separate matrices corresponding to the intensities of red, green, and blue in the image. If the image size is 256 * 256 pixels, then three 256 * 256 matrices (two-dimensional arrays) can represent the image in the computer. One can imagine stacking the three matrices representing the colors on top of each other to reveal the original appearance of the image.

Now that we have the representation of the image in the computer, how do we input it into the neural network?

Typically, we convert the three matrices into a vector, which can be understood as a 1 * n (row vector) or n * 1 (column vector) array. The total dimension of this vector is 256 * 256 * 3, resulting in 196608. In the field of artificial intelligence, each piece of data input into the neural network is called a feature, so the image above has 196608 features. This 196608-dimensional vector is also called a feature vector. The neural network receives this feature vector as input, makes predictions, and then provides the corresponding results.

2. Text Input Processing

Text is composed of a series of characters, and first, it needs to be segmented into meaningful words, a process called tokenization. After tokenization, a vocabulary consisting of all the words or some high-frequency words that appear is constructed (an existing vocabulary can also be used). Each word in the vocabulary is assigned a unique index, allowing the text to be converted into a discrete sequence of symbols, making it easier for the neural network to process. Before inputting into the neural network, the symbol sequence of the text is usually converted into a dense vector representation.

For example, for the text “How does neural network work?”:

• Tokenization: [“how”, “does”, “neural”, “network”, “work”]
• Constructing Vocabulary: {“how”: 0, “does”: 1, “neural”: 2, “network”: 3, “work”: 4}
• Serializing Text Data: [“how”, “does”, “neural”, “network”, “work”] –>[0, 1, 2, 3, 4]
• Vectorization:

# Using one-hot vector representation as an example:
[[1, 0, 0, 0, 0]
 [0, 1, 0, 0, 0]
 [0, 0, 1, 0, 0]
 [0, 0, 0, 1, 0]
 [0, 0, 0, 0, 1]]

Finally, the vector sequence is used as input for training or predicting with the neural network.

Now that we understand how data is input into the neural network, how does the neural network train based on this data?

How Neural Networks Make Predictions

First, let’s clarify the difference between model training and prediction: training refers to adjusting the model’s parameters using a known dataset so that it can learn the relationship between inputs and outputs; prediction refers to using a trained model to make predictions on new input data.

The prediction made by the neural network is actually based on a very simple linear transformation formula:

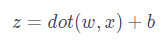
Here, x represents the feature vector, w is the weight of the feature vector, indicating the importance of each input feature, and b is the threshold that influences the prediction result. The dot() function in the formula represents the vector multiplication of w and x. For example, if an input data has i features, substituting into the formula yields:

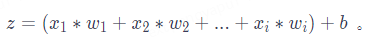
How do we understand this formula? Suppose you need to decide whether to go boating in the park this weekend, and you are hesitating. You need the neural network to help you make the decision. The decision to go boating depends on three factors: whether the weather is sunny and warm, whether the location is at a moderate distance, and whether the companions are agreeable. The actual situation is that the weather is cloudy with occasional gusts, the location is in a remote suburb 20 km away, and the companion is the handsome guy you have long admired. These three factors are the input data’s feature vector x = [x1, x2, x3]. We need to set the feature values according to the impact of the features on the result. For instance, “bad weather” and “remote location” have negative impacts on the result, so we can set them as -1, while “the handsome guy is your long-time crush” clearly has a positive impact, so we can set it as 1, resulting in the feature vector x = [-1, -1, 1]. Next, we need to set the weights for the three features according to their influence on your final decision. If you don’t care about the weather or location, as long as you are with the handsome guy, you can set the weights as w = [1, 1, 5]; if you are lazy, you might set the weights as w = [2, 6, 3]; in short, the weights are determined by the importance of the corresponding features.

We choose the first set of weights w = [1, 1, 5] and the feature vector x = [-1, -1, 1], setting the threshold b = 1. Assuming the result z ≥ 0 means go, and z < 0 means don’t go, we calculate the prediction result z = (x1*w1 + x2*w2 + x3*w3) + b = 4 > 0, hence the neural network’s prediction is: go boating in the park.

The formula used above

Essentially, this is a form of logistic regression used to map input data to binary classification probabilities. Logistic regression typically uses a specific activation function to achieve the mapping of z values to [0, 1], namely the Sigmoid function, which transforms the results of linear transformations into probability values through nonlinear mapping. Generally, a probability value greater than or equal to 0.5 is considered positive, while a value less than 0.5 is considered negative.

The formula and graph of the Sigmoid function are as follows:

In addition to controlling the output range between 0 and 1, the Sigmoid function (or other activation functions) plays another important role: it performs nonlinear mapping of the results of linear transformations, allowing neural networks to learn and represent more complex nonlinear relationships. Without activation functions, neural networks can only solve simple linear problems; however, with sufficient layers, neural networks can solve all problems, making activation functions essential.

How Neural Networks Learn

After obtaining the prediction result, the neural network will use the loss function to determine whether the prediction result is accurate. If it is not accurate enough, the neural network will adjust itself, which is the learning process.

The loss function is used to measure the error between the model’s prediction result and the true label. By comparing the predicted values with the true values, the loss function provides a numerical indicator reflecting the model’s current prediction performance. A smaller loss value indicates that the model’s prediction is closer to the true labels, while a larger loss value indicates a greater prediction error. Below is a commonly used loss function for binary classification (log loss):

The purpose of neural network learning is to adjust the model parameters to minimize the loss function, thereby improving the model’s prediction performance. This process is also known as model training. The gradient descent algorithm can solve this problem by finding suitable w (feature weights) and b (thresholds). The gradient descent algorithm gradually changes the values of w and b to make the loss function result smaller, thus making the prediction results more accurate.

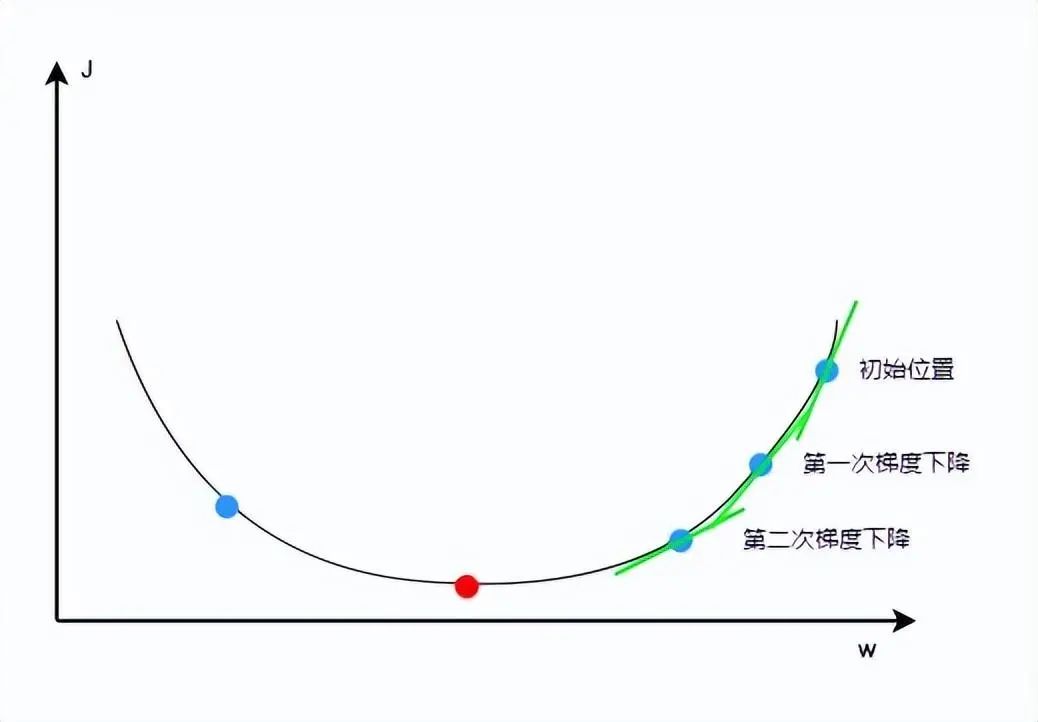
It is important to note that if the learning rate is set too low, it will take many gradient descent steps to reach the lowest point, wasting machine resources; if set too high, it may miss the lowest point and go directly to the point on the left in the graph. Therefore, it is necessary to choose the correct learning rate based on the actual situation.

The computational process of neural networks mainly involves two steps: forward propagation and backward propagation. Forward propagation is used to compute the output of the neurons, which is the process of weighted summation of the input features and nonlinear transformation through the activation function; backward propagation is used to update and optimize the model parameters by calculating the gradient of the loss function with respect to the model parameters and propagating the gradient backward from the output layer to the input layer (backward propagation involves a lot of mathematical calculations, which interested readers can explore further).

4. Conclusion

In summary, the process of training and learning in neural networks is essentially about continuously tuning the model parameters to reduce the prediction loss value. After sufficient training, the model can learn effective feature representations and weight distributions from the input data, enabling it to make accurate predictions on unseen data. The trained neural network model can be applied to various practical problems. For instance, in image classification tasks, convolutional neural networks can automatically recognize objects or patterns based on the features of input images; in natural language processing tasks, recurrent neural networks can understand and generate text; in recommendation systems, multi-layer perceptron neural networks can provide personalized recommendations based on users’ historical behaviors.

This article provides a shallow explanation of the working mechanism of neural networks. If there are inaccuracies, please feel free to provide feedback!

Source of this article: Author: Ouyang Zhouyu from JD Cloud Developer – JD Retail Link: https://my.oschina.net/u/4090830/blog/10320660 . For the purpose of transmission and sharing, it does not represent the platform’s endorsement of its views or responsibility for its authenticity. The copyright belongs to the original author. If there is any infringement, please contact us for removal.