
0
Table of Contents
HorNet: Efficient High-Order Spatial Interactions with Recursive Gated Convolutions (from Tsinghua University, Zhou Jie, Lu Jiwen team, Meta AI) HorNet Principle Analysis 1 Background and Motivation 2 Introduction to HorNet 3 Conv: Gated Convolutions Achieve First-Order Spatial Interactions 4 Conv: High-Order Gated Convolutions Achieve High-Order Spatial Interactions 5 Computational Complexity of Conv 6 Long-Distance Interactions with Large Convolution Kernels 7 Connection with Self-Attention 8 HorNet Model Architecture 9 Experimental Results
Paper Title: HorNet: Efficient High-Order Spatial Interactions with Recursive Gated Convolutions
Paper Link:
http://arxiv.org/pdf/2207.14284.pdf
1
Background and Motivation
This paper proposes a general visual model based on recursive gated convolutions, which is a valuable exploration in the field of general visual models by scholars from Tsinghua University, Zhou Jie, Lu Jiwen team, and Meta AI.
Convolutional Neural Networks (CNNs) have driven significant advancements in deep learning and computer vision. Due to a series of inherent advantages, CNNs are naturally suited for many computer vision tasks. One such advantage is translation equivariance, which introduces an inductive bias into CNN models, allowing them to adapt to input images of varying sizes. Meanwhile, CNNs have been around for a long time, and the community has contributed many highly optimized implementations, making them very efficient on high-performance GPUs and edge devices.
The development of visual Transformer models has also shaken the dominance of CNNs. By borrowing some excellent architectural design ideas (pyramid structure, inductive bias, residual connections, etc.) and training strategies (knowledge distillation, etc.) from CNNs, visual Transformer models have achieved outstanding performance comparable to CNNs in downstream tasks such as image classification, object detection, and semantic segmentation.
People can’t help but wonder: what exactly makes visual Transformer models perform better than CNNs?
This question is difficult to answer well, but we don’t necessarily need to fully answer it; we can start by borrowing characteristics from visual Transformer models to design more powerful CNN models.
For example, the architecture design of visual Transformers generally follows a meta-architecture, where although the types of token mixers may vary (Self-attention, Spatial MLP, Window-based Self-attention, etc.), the basic macro architecture typically consists of four stages forming a pyramid structure. For instance:
-
ConvNeXt[1] borrowed this macro architecture and constructed a series of high-performance CNN architectures using 7×7 Depth-wise Convolutions. -
GFNet[2] borrowed this macro architecture and constructed a series of high-performance generic Backbone architectures using 2D-FFT Fourier transforms and 2D-IFFT inverse transforms. -
RepLKNet[3] borrowed this macro architecture and constructed a series of high-performance generic Backbone architectures using 31×31 large kernel convolutions and structural reparameterization schemes.
In the features of a model, there may exist complex and high-order interactions between any two spatial positions, and we hope to explicitly model these interactions in the model. The success of Self-attention actually proves that explicitly modeling high-order interactions is beneficial for enhancing the model’s expressive power.
However, it seems that recent works in convolutional neural networks have not yet recognized the need to explicitly model high-order interactions, which is also the motivation of this paper.
2
Introduction to HorNet
As shown in Figure 1, this is a diagram illustrating the core idea of this paper: analyzing the interactions of features (red blocks) and their surrounding areas (gray blocks) in different operations. (a) Ordinary convolution operations do not consider spatial information interactions. (b) Dynamic convolution operations utilize dynamic weights to consider the interactions of surrounding areas, enhancing model performance. (c) Self-attention operations achieve second-order spatial information interactions through two consecutive matrix multiplications of query, key, and value. (d) The method proposed in this paper can efficiently achieve arbitrary-order information interactions using gated convolutions and recursive operations. The basic trend of visual modeling indicates that the model’s expressive power can be improved by increasing the order of spatial interactions.
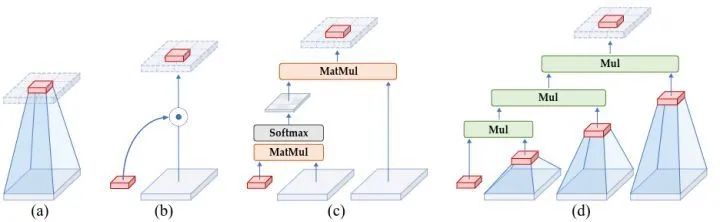
Figure 1: Diagram illustrating the core idea of this paper: analyzing the interactions of features (red blocks) and their surrounding areas (gray blocks) in different operations. (a) Ordinary convolution operation (b) Dynamic convolution operation (c) Self-attention operation (d) The method proposed in this paper
In this paper, the authors attribute the key factors for the success of visual Transformers to dynamic weights (referring to the values of the attention matrix being related to specific inputs, input-adaptive), long-distance modeling (long-range), and high-order spatial interactions (high-order). Previous works such as ConvNeXt[1], GFNet[2], and RepLKNet[3] satisfy the properties of dynamic weights and long-distance modeling, but they have not considered how to enable a convolutional neural network to achieve high-order spatial interactions.
To address this, the authors propose a Recursive Gated Convolution (Conv) based on recursion and gated convolutions, allowing convolutional neural networks to also perform high-order spatial interactions. Conv has several excellent features, such as:
-
Efficient: The convolution-based implementation avoids the quadratic complexity of Self-attention. Moreover, the pyramid design that gradually increases channel width during spatial interaction can achieve high-order spatial interactions under limited complexity constraints. -
Scalable: The authors extend the second-order interactions in Self-attention to arbitrary orders to further enhance modeling capabilities. Since no assumptions are made about the types of convolutions, Conv can accommodate various convolution kernels, such as 31×31 large convolution kernels or 2D. -
Translation Equivariance: Conv inherits the translation equivariance of standard convolutions, introducing inductive bias for visual tasks, avoiding the shortcomings of attention mechanisms that cannot achieve inductive bias.
Based on Conv and the general principles of designing universal visual architectures, the authors construct a series of visual backbone models called HorNet, and validate its performance on a series of dense prediction tasks.
3
g^n Conv: Gated Convolutions Achieve First-Order Spatial Interactions
Conv aims to achieve long-distance modeling and high-order spatial interactions. It is constructed using standard convolutions, linear projection operations, and element-wise multiplication, but possesses input-adaptive functionality similar to Self-attention.
Self-attention matrices used to mix spatial token information have weights related to the input. However, the complexity of Self-attention is quadratically related to the input resolution of the image, resulting in significant computational costs for high-resolution downstream tasks. In this work, the authors utilize efficient convolutions and fully connected layers to perform spatial information interactions.
The basic operation of recursive gated convolutions is gated convolution (Conv), where the input feature is , and the output of the gated convolution Conv can be written as:
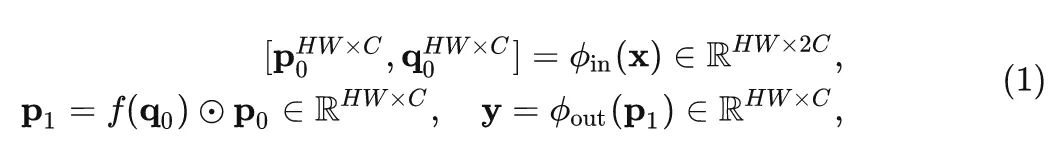
In the above expression, is the linear projection operation that accomplishes information exchange in the channel dimension, and is the Depth-wise convolution.
Note that , where is the local window of Depth-wise Conv, and the center coordinate is the weight of Depth-wise Conv.
The above expression can be regarded as the first-order interaction between and its surrounding features.
4
g^ Conv: High-Order Gated Convolutions Achieve High-Order Spatial Interactions
Gated convolutions (Conv) can achieve first-order interactions between a feature and its surrounding features. Next, the authors design Conv to achieve long-distance modeling and high-order spatial interactions. First, a series of projected features and are obtained through :
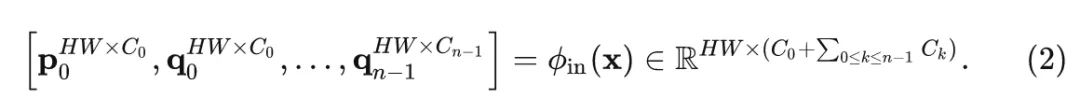
Then perform gated convolutions recursively:
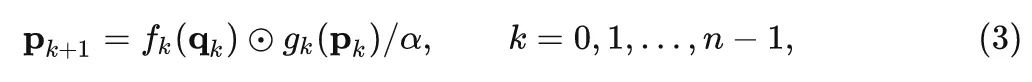
In the above expression, each recursive process is divided by to stabilize training, and is a series of Depth-wise convolution operations used to match the number of channels of features during each recursive process.
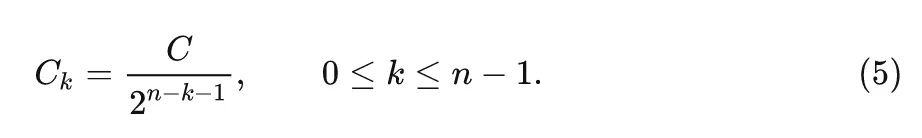
Finally, the output of the last recursion is input into the projection layer to obtain the result of . This can achieve the -order interaction between a feature and its surrounding features.
However, to compute the expression, it is not necessary to compute times; instead, it can be completed by directly applying a Depth-wise Convolution to the combined features, which can further simplify the implementation on GPUs and improve efficiency.
To ensure that high-order interactions do not introduce excessive computational overhead, the authors set the channel dimensions of each order to an exponentially decreasing form:
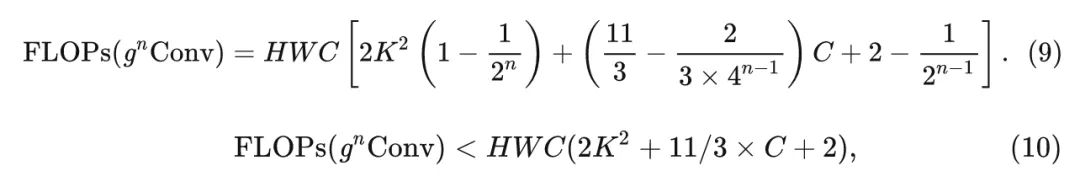
5
Computational Complexity of g^n Conv
The computation of Conv can be divided into three parts.
The first and last projection layers and :
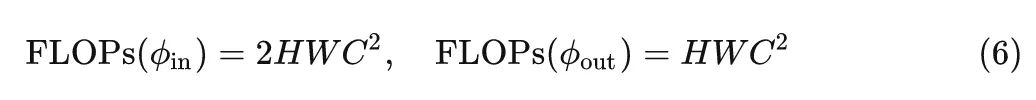
Depth-wise Convolution:
The computational cost of Depth-wise convolution with kernel size is applied to feature , where . Therefore, the computational load for this part is:
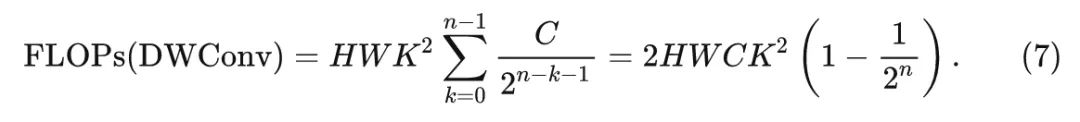
The computational load for dimension matching in recursive gated operations:
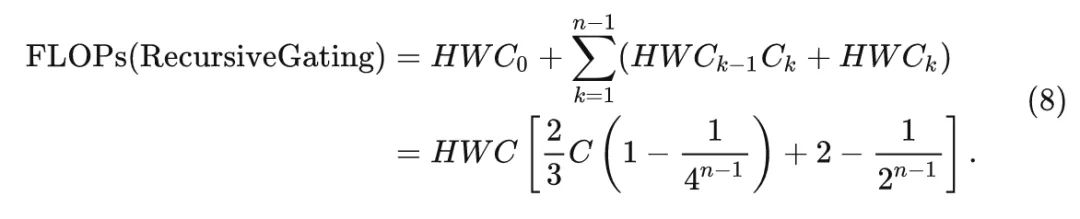
Thus, the total computational load is:
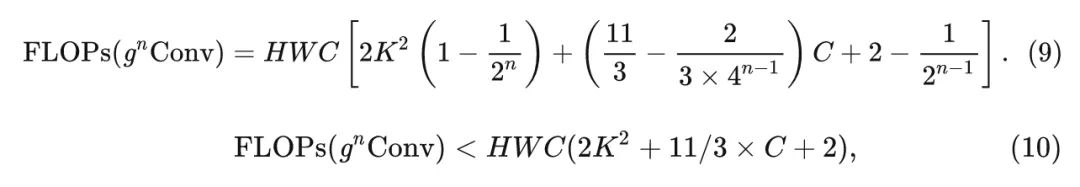
6
Long-Distance Interactions with Large Convolution Kernels
Another difference between visual Transformers and traditional CNNs is the size of the receptive field. Traditional CNNs typically use 3×3 convolutions throughout the network, while visual Transformers compute Self-attention over relatively large local windows (e.g., 7×7) across the entire feature map. To enable Conv to model long-distance interactions, the authors adopt two forms of Depth-wise convolutions:
-
7×7 Depth-wise Convolution (ConvNeXt[1]): This is the default receptive field size for Swin and ConvNeXt. It has been validated to exhibit excellent properties across various visual tasks. The PyTorch code is as follows:
def get_dwconv(dim, kernel, bias):
return nn.Conv2d(dim, dim, kernel_size=kernel, padding=(kernel-1)//2 ,bias=bias, groups=dim)-
Global Filter (GFNet[2]): By transforming features from the spatial domain to the frequency domain using 2D-FFT, the element-wise multiplication operation in the frequency domain is equivalent to a spatial convolution with global kernel size and circular padding in the spatial domain. In practical implementation, the channels are divided into two parts, one part through Global Filters and the other through 3×3 Depth-wise Convolution. The PyTorch code is as follows:
class GlobalLocalFilter(nn.Module):
def __init__(self, dim, h=14, w=8):
super().__init__()
self.dw = nn.Conv2d(dim // 2, dim // 2, kernel_size=3, padding=1, bias=False, groups=dim // 2)
self.complex_weight = nn.Parameter(torch.randn(dim // 2, h, w, 2, dtype=torch.float32) * 0.02)
trunc_normal_(self.complex_weight, std=.02)
self.pre_norm = LayerNorm(dim, eps=1e-6, data_format='channels_first')
self.post_norm = LayerNorm(dim, eps=1e-6, data_format='channels_first')
def forward(self, x):
x = self.pre_norm(x)
x1, x2 = torch.chunk(x, 2, dim=1)
x1 = self.dw(x1)
x2 = x2.to(torch.float32)
B, C, a, b = x2.shape
x2 = torch.fft.rfft2(x2, dim=(2, 3), norm='ortho')
weight = self.complex_weight
if not weight.shape[1:3] == x2.shape[2:4]:
weight = F.interpolate(weight.permute(3,0,1,2), size=x2.shape[2:4], mode='bilinear', align_corners=True).permute(1,2,3,0)
weight = torch.view_as_complex(weight.contiguous())
x2 = x2 * weight
x2 = torch.fft.irfft2(x2, s=(a, b), dim=(2, 3), norm='ortho')
x = torch.cat([x1.unsqueeze(2), x2.unsqueeze(2)], dim=2).reshape(B, 2 * C, a, b)
x = self.post_norm(x)
return xConv’s PyTorch code is as follows:
class gnconv(nn.Module):
def __init__(self, dim, order=5, gflayer=None, h=14, w=8, s=1.0):
super().__init__()
self.order = order
self.dims = [dim // 2 ** i for i in range(order)]
self.dims.reverse()
self.proj_in = nn.Conv2d(dim, 2*dim, 1)
if gflayer is None:
self.dwconv = get_dwconv(sum(self.dims), 7, True)
else:
self.dwconv = gflayer(sum(self.dims), h=h, w=w)
self.proj_out = nn.Conv2d(dim, dim, 1)
self.pws = nn.ModuleList(
[nn.Conv2d(self.dims[i], self.dims[i+1], 1) for i in range(order-1)]
)
self.scale = s
print('[gnconv]', order, 'order with dims=', self.dims, 'scale=%.4f'%self.scale)
def forward(self, x, mask=None, dummy=False):
B, C, H, W = x.shape
fused_x = self.proj_in(x)
pwa, abc = torch.split(fused_x, (self.dims[0], sum(self.dims)), dim=1)
dw_abc = self.dwconv(abc) * self.scale
dw_list = torch.split(dw_abc, self.dims, dim=1)
x = pwa * dw_list[0]
for i in range(self.order -1):
x = self.pws[i](x) * dw_list[i+1]
x = self.proj_out(x)
return x7
Connection with Self-Attention
This section aims to demonstrate that Conv also possesses input adaptive capabilities.
The output of Multi-head Self-attention can be expressed as:
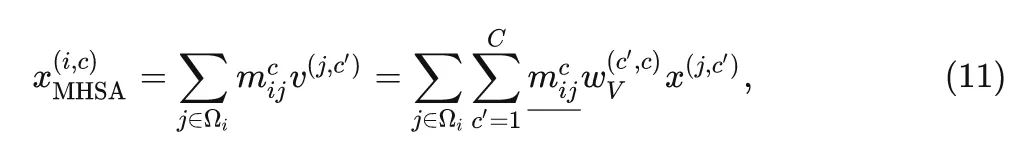
In the above expression, are the weights of the projection layer, and are obtained through dot-product operations.
From expression 11, it can be seen that Self-attention has input adaptive capabilities because is related to input index.
The output of Conv can be expressed as:
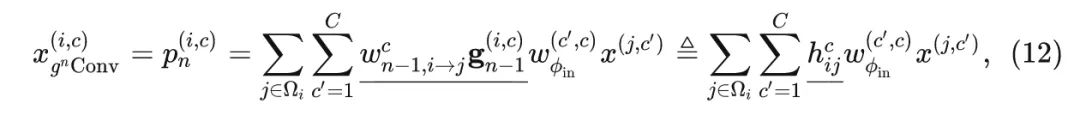
In the above expression, are the weights of Depth-wise convolution, are the weights of the linear projection layer, and is the projection process to the -th recursive operation.
From expression 12, it can also be seen that Conv has input adaptive capabilities because is related to input index. The difference between Conv and Self-attention lies in the fact that is computed from , while it contains -order spatial interaction effects.
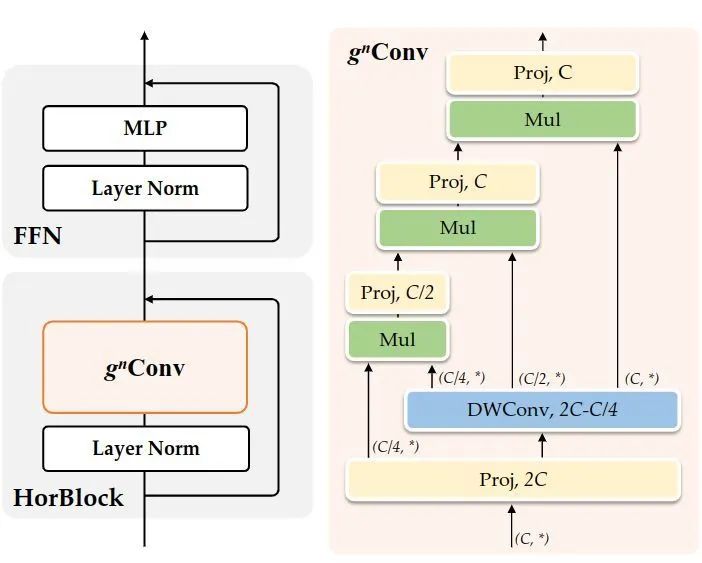
Figure 2: HorNet Model Architecture
8
HorNet Model Architecture
HorNet
Using Conv as the Token Mixer and based on the Swin architecture, the authors designed a series of general visual architectures called HorNet. The basic block consists of a Token Mixer and a FFN layer. Depending on whether Conv uses Depth-wise Convolution or GF Layer, it is divided into HorNet-T/S/B/L and HorNet-T/S/B/L. According to Swin’s overall architecture, it is also structured into 4 stages, with the number of channels in each stage being , for HorNet-T/S/B/L, the number of channels is . The number of high-order interactions in each stage is .
HorFPN
The authors further use Conv as an enhanced alternative to standard convolutions. Therefore, they replaced the convolution operations used for feature fusion in FPN with Conv to improve the spatial interaction capabilities of downstream tasks. Specifically, after integrating features from different pyramid levels, Conv is added. For object detection tasks, Conv replaces the convolutions in FPN. For semantic segmentation tasks, Conv replaces the convolutions after concatenating features.
9
Experimental Results
ImageNet-1K Image Classification
Experimental setup without using ImageNet-22K pre-training: directly trained on ImageNet-1K for 300 epochs.
Experimental setup using ImageNet-22K pre-training: first pre-trained on ImageNet-22K for 90 epochs, then trained on ImageNet-1K for 30 epochs.
The results are shown in Figure 3. It can be seen that the HorNet model achieves highly competitive performance compared to state-of-the-art Transformers and CNNs, surpassing Swin and ConvNeXt. Furthermore, the HorNet model generalizes well to larger image resolutions, larger model sizes, and more training data, demonstrating the effectiveness and universality of the HorNet model.
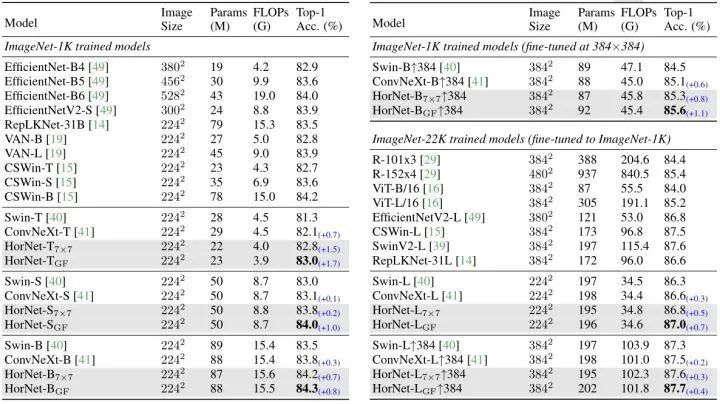
Figure 3: Image Classification Experimental Results on ImageNet
Semantic Segmentation Experimental Results
Dataset: ADE20K, segmentation head UperNet, iterations, AdamW as optimizer, batch size set to 16, the results are shown in Figure 4. The HorNet and HorNet models with similar model parameter counts and FLOPs outperform Swin and ConvNeXt models. Specifically, the HorNet GF model achieves better results in single-scale mIoU than HorNet and ConvNeXt series, indicating that the global interactions captured by the global filter help with semantic segmentation. Moreover, the HorNet-L and HorNet-L GF models even have about 25% fewer FLOPs than ConvNeXt-XL. These results clearly demonstrate the effectiveness and scalability of HorNet in semantic segmentation.
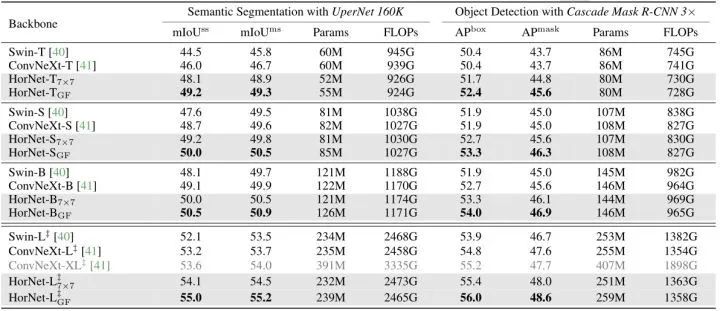
Figure 4: Semantic Segmentation Experimental Results
Object Detection and Instance Segmentation Experimental Results
Dataset: COCO, segmentation head Mask R-CNN, results are shown in Figure 4. The HorNet model shows better performance than Swin/ConvNeXt models of the same size in both box AP and mask AP. Compared to ConvNeXt, the HorNet GF series achieves an increase of +1.2 ~ 2.0 in box AP and +1.0 ~ 1.9 in mask AP.
Dense Prediction Experimental Results
In this section of the experiment, the authors aim to demonstrate that the proposed Conv serves as a better fusion module, capable of capturing high-order interactions between features at different levels in dense prediction tasks. Specifically, after replacing FPN with HorFPN, the results are shown in Figure 5. For object detection and semantic segmentation tasks, it can be observed that HorFPN significantly reduces FLOPs (approximately 50%) while achieving better mIoU.
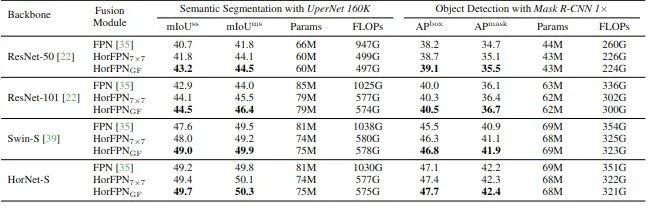
Figure 5: Dense Prediction Experimental Results
Ablation Study Results
(a) Ablation Study of
The results of the ablation study are shown in Figure 6 (a). The accuracy of Swin-T is , and both the SE module and Conv can enhance the baseline model. The authors find that gradually increasing (i.e., ) across the 4 stages can further improve performance. These results indicate that Conv is an efficient and scalable operation that can better capture high-order spatial interactions than Self-attention and Depth-wise Convolution.
(b) Experiments on Isotropic Architectures
The authors also evaluated Conv on isotropic architectures. They replaced the Self-attention operation in DeiT-S with Conv and adjusted the number of blocks to 13 to obtain the isotropic HorNet model. The comparison in Figure 6 (b) shows that isotropic HorNet-S significantly outperforms DeiT-S. These results indicate that Conv can better achieve the functions of Self-attention compared to ordinary convolutions and has superior capabilities in simulating complex spatial interactions.
(c) Experiments on Other Operations
To further demonstrate the versatility of Conv, the authors used Depth-wise Convolution and Pool operations as the basic operations for Conv. The results in Figure 6 (c) indicate that Conv can significantly enhance the performance of these two operations, suggesting that Conv may be even stronger when equipped with better basic operations.

Figure 6: Ablation Study Results
10
Conclusion
This paper proposes a general visual model HorNet based on recursive gated convolutions Conv. In this paper, the authors attribute the key factors for the success of visual Transformers to dynamic weights (referring to the values of the attention matrix being related to specific inputs, input-adaptive), long-distance modeling (long-range), and high-order spatial interactions (high-order). Previous works have satisfied the properties of dynamic weights and long-distance modeling, but they have not considered how to enable a convolutional neural network to achieve high-order spatial interactions. Conv can serve as a plug-and-play Token Mixer to replace the attention layers in visual Transformers; it is efficient, scalable, and possesses translation equivariance. The authors have also demonstrated the effectiveness of HorNet in common visual recognition tasks through extensive experiments.
References
-
^abcA ConvNet for the 2020s -
^abcGlobal Filter Networks for Image Classification -
^abScaling Up Your Kernels to 31×31: Revisiting Large Kernel Design in CNNs

Scan the QR code to add the assistant on WeChat
About Us

