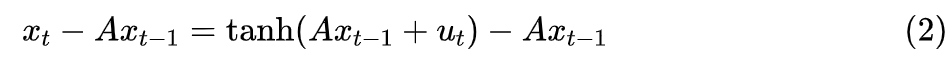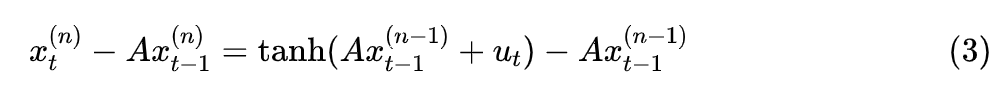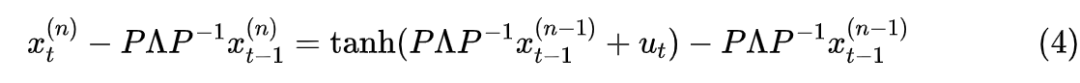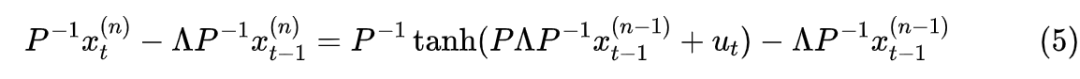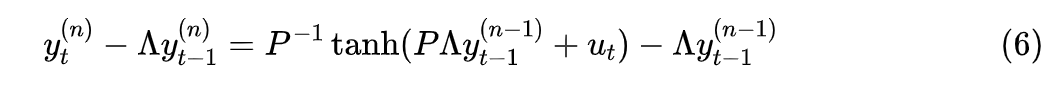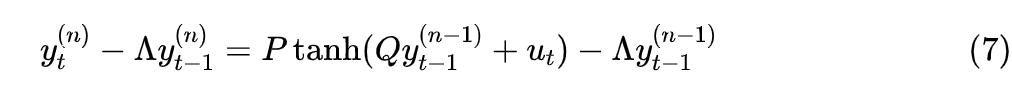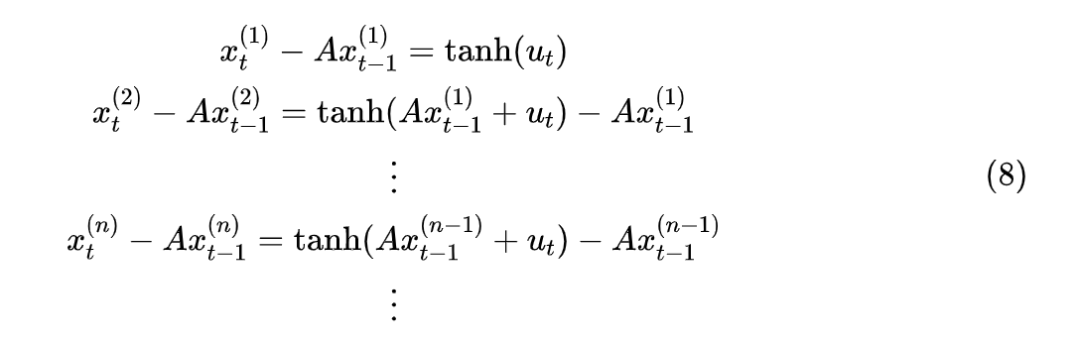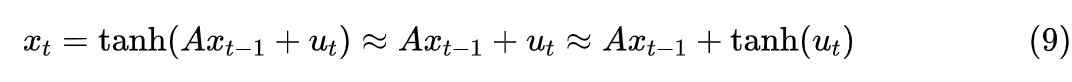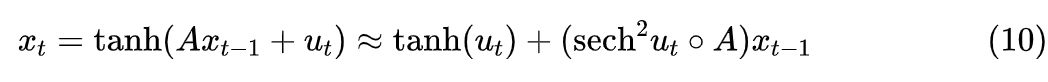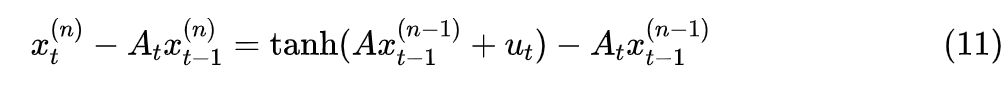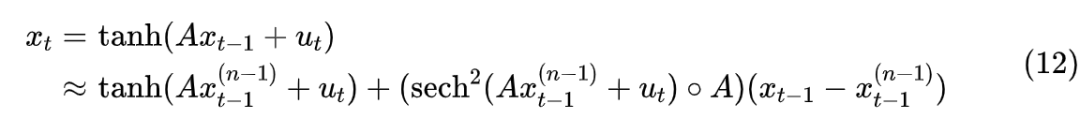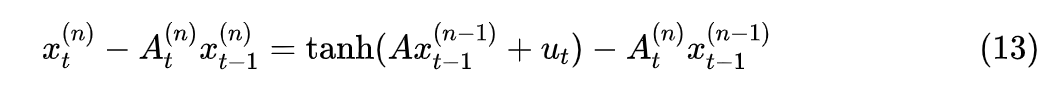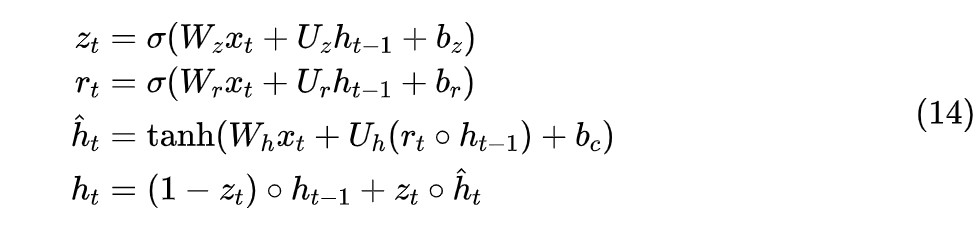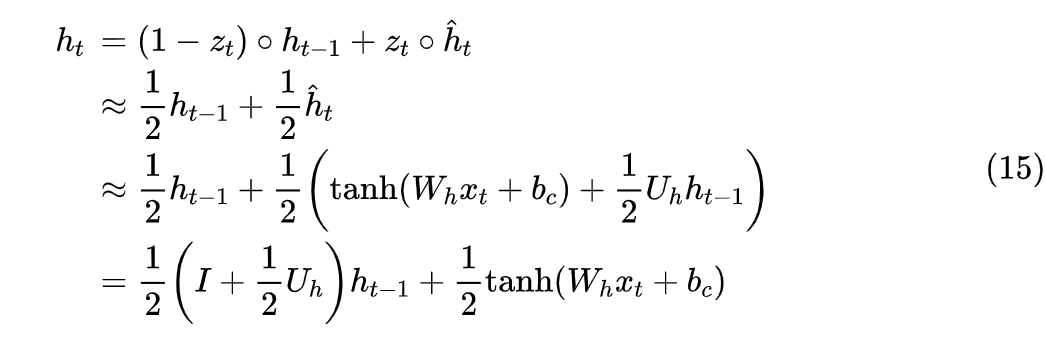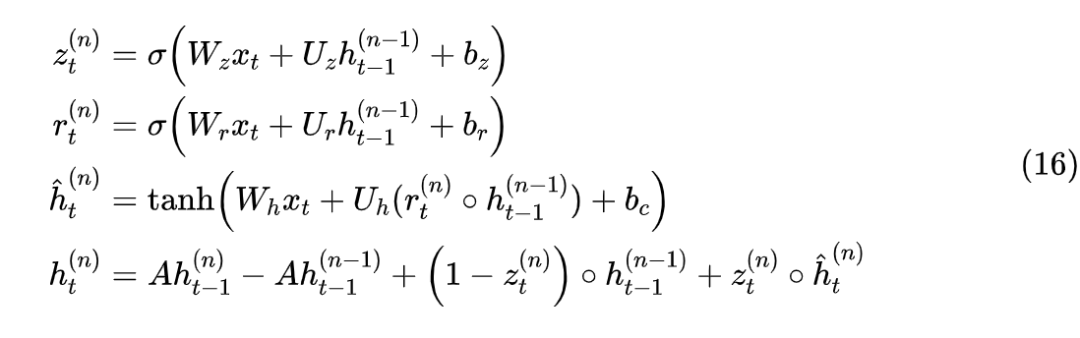©PaperWeekly Original · Author | Su Jianlin
Affiliation | Scientific Space
Research Direction | NLP, Neural Networks
In recent years, linear RNNs have attracted some researchers’ attention due to their characteristics such as parallel training and constant inference costs (for example, my previous article titled “Google’s New Work Attempts to ‘Revive’ RNN: Can RNN Shine Again?”). This allows RNNs to still have a “place” in the trend where Transformers are flourishing everywhere. However, it seems that this “place” only belongs to linear RNNs, as non-linear RNNs cannot be efficiently parallel trained, making them “powerless” in the architectural competition.
However, a paper titled “Parallelizing Non-Linear Sequential Models over the Sequence Length” has a different viewpoint. It proposes an iterative algorithm that claims to enable parallel training of non-linear RNNs! Is it really that magical? Let’s explore.

Paper Title:
Parallelizing Non-Linear Sequential Models over the Sequence Length
https://arxiv.org/pdf/2309.12252.pdf
Finding Fixed Points
The original paper provides a very general introduction to its methods, focusing on PDEs and ODEs. Here, we will directly tackle RNNs. Consider a common simple non-linear RNN:

Due to the presence of , it can only be computed serially.Now we subtract from both sides:
Of course, this does not change the essence of it being a non-linear RNN. However, we can see that if we replace the right side’s with a given vector like , then it becomes a linear RNN, which, according to the results from “Google’s New Work Attempts to ‘Revive’ RNN: Can RNN Shine Again?”, can be computed in parallel. At this point, agile readers may have guessed the next steps—iterative solving!
First, we change the above RNN to
Starting from the given , we repeatedly iterate the above equation, ideally converging to a fixed point , which is the original computation result of the non-linear RNN. Of course, theoretically, the total computational load of iterating through equation (3) is greater than directly computing through equation (1) recursively, but since each iterative step is a parallelizable linear RNN, and if the convergence speed is relatively fast, the number of iterations does not need to be too many, then the total time consumption is usually faster than direct non-linear RNN recursion (especially when the sequence length is large).

In fact, the reason why non-linear RNNs are slow and cannot be parallel computed is secondary; the key issue is that they involve a lot of non-element-wise operations, such as the matrix operations inside equation (1); while linear RNNs are fast not only because they allow parallel training but also because they can diagonalize to convert matrix multiplication into element-wise multiplication—element-wise multiplication is not too slow even in serial computation.
When we convert the non-linear RNN to a linear RNN iteration through equation (3), we also enjoy the “treatment” of linear RNNs being diagonalizable, thus improving computation speed. Specifically, in the complex domain, diagonalizing A to , then equation (3) becomes
Multiplying both sides by :
Letting , the above equation can be simplified to
Since RNNs are generally followed by a projection layer, the P in principle can be merged into the external projection layer, meaning that the above equation theoretically has the same expressive power as the original (1). However, since is a diagonal matrix, the recursive computational load will be significantly reduced. The above equation also introduces the inverse matrix, which not only increases the computational load but also complicates optimization, so we can simply replace and with two unrelated parameter matrices:
As long as the initialization is .

Perturbation Idea
Assuming , then equation (3) actually decomposes the original non-linear RNN into a series of linear RNNs:
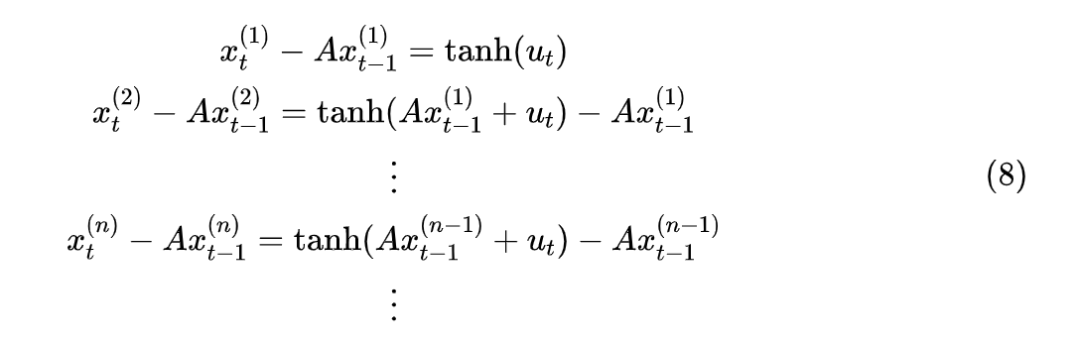
Assuming are small quantities, then using on the right side of equation (1) yields:
This is exactly the first equation in (8), so if the assumption holds, then might already be close enough to the ideal . From here we can see that “subtracting from both sides” is the key point, making the first iterative step of (3) close to the first-order linear approximation of the original non-linear RNN, which can improve convergence speed. This is a classic operation in mathematical physics known as “perturbation”.
According to the idea of perturbation methods, the key to improving convergence speed is to enhance the accuracy of the approximate expansion. A relatively simple improvement is to assume that is a small quantity, then according to the first-order Taylor expansion:
Thus, the improved result is that equation (3) becomes
Where . A more refined improvement is to expand based on the previous iteration result at each iterative step:
Thus, equation (3) becomes
Where . The final iterative format is essentially the “Newton’s method” for solving numerical equations, which has quadratic convergence speed.
Theoretically, equations (11) and (13) can indeed improve convergence speed; however, they make the matrix A of each linear recursion relate to t or even n, which greatly increases the complexity of parallelization and does not utilize the diagonalization technique from the “Simplified Form” section to accelerate. On the other hand, if we maintain the iterative format like (3), although there are many efficiency benefits, the convergence cannot be well guaranteed.
Does this contradiction between the two approaches have no way to reconcile? In fact, according to my perspective, the most straightforward approach is to “not worry about it”—after deriving (3) from the non-linear RNN, forget about the original non-linear RNN and treat (3) as the basic model. In other words, why worry whether (3) converges to the original non-linear RNN? Isn’t it better to treat it as a new starting point? The results learned by gradient descent are what they are; if the results learned by gradient descent do not converge to the original non-linear RNN, it means that not converging to the original RNN is more suitable.
Once we break free from this mental constraint, many issues become clear. First, even if equation (13) theoretically has very good convergence speed, it is conditional, and under the context of deep learning, ensuring these conditions can be quite extravagant. In other words, even the convergence of equation (13) is not absolutely guaranteed, so why should we criticize (3) for being “fifty steps laughing at a hundred steps”? Secondly, treating (3) as a new starting point allows us to understand it purely as a new use of linear RNNs, or an idea to address the shortcomings of linear RNNs (e.g., linear RNNs are not Turing complete), making it more operational.
Overall, ignoring its convergence seems to break the mental deadlock and explore more general results.

General Cases
The previous lengthy discussions revolved around the simple non-linear RNN, which is equation (1). What about more commonly used LSTM and GRU?
Taking GRU as an example, its original form is
In the initial stage, all gates can be approximately viewed as , then mimicking equation (9) gives
Thus, we can select , and rewrite GRU as an iteration
Overall, this transformation of non-linear RNNs into linear RNN iterations, from a practical perspective, leads to a method of parameter sharing and combination of multi-layer linear RNNs based on non-linear RNNs. After several iterations, the computational load of several layers of linear RNNs is naturally triggered. This raises a thought: unless it can be proven that non-linear RNNs like GRU and LSTM have absolute advantages, wouldn’t it be better to directly stack several layers of “linear RNN + MLP”?
Article Summary
This article briefly discusses the parallel computation issue of non-linear RNNs—through the “perturbation” idea in mathematical physics, we can convert non-linear RNNs into linear RNN iterations, thereby utilizing the parallelism of linear RNNs to achieve parallelism in non-linear RNNs.



Let Your Words Be Seen by More People
How can more quality content reach the reader group in a shorter path, reducing the cost of readers finding quality content? The answer is: people you don’t know.
There are always some people you don’t know who know what you want to know. PaperWeekly may serve as a bridge to facilitate the collision of scholars and academic inspirations from different backgrounds and directions, generating more possibilities.
PaperWeekly encourages university laboratories or individuals to share various quality content on our platform, which can be latest paper interpretations, analysis of academic hotspots, research insights, or competition experience explanations, etc. Our only goal is to make knowledge truly flow.
📝 Basic Requirements for Submissions:
• The article must indeed be a personal original work and has not been published in public channels. If it is an article already published or pending publication on other platforms, please indicate clearly.
• Manuscripts are recommended to be written in markdown format, and images in the text should be sent as attachments, requiring clear images with no copyright issues.
• PaperWeekly respects the author’s right to attribution and will provide competitively priced remuneration for each accepted original first-published manuscript, specifically based on the article’s readership and a tiered quality assessment.
📬 Submission Channel:
• Submission Email:[email protected]
• Please include your immediate contact information (WeChat) in your submission so we can contact the author as soon as the manuscript is selected.
• You can also directly add the editor’s WeChat (pwbot02) for quick submission, noting: Name – Submission.

△ Long press to add PaperWeekly editor
🔍
Now, you can also find us on “Zhihu”
Search for “PaperWeekly” on the Zhihu homepage
Click “Follow” to subscribe to our column