Doctoral Innovation Forum
Issue Seventy
On the morning of March 1, 2024, the seventieth issue of the Doctoral Innovation Forum was held online.PhD student Qin Yubin from Tsinghua University’s School of Integrated Circuits presented an academic report titled “High-Efficiency Attention Model Architecture Design”. The report focuses on the attention-based Transformer model, discussing optimization methods for attention operators and layers in response to issues such as high computational load, diverse computational operators, and severe memory bottlenecks.Dr. Qin Yubin was invited to provide a detailed written commentary for this report, with a recommended reading and highlights of the Q&A session attached at the end. Let’s revisit the exciting report of the seventieth issue through text and video together!

01. Report Outline

02. Background Introduction and Main Content
1. Attention Models
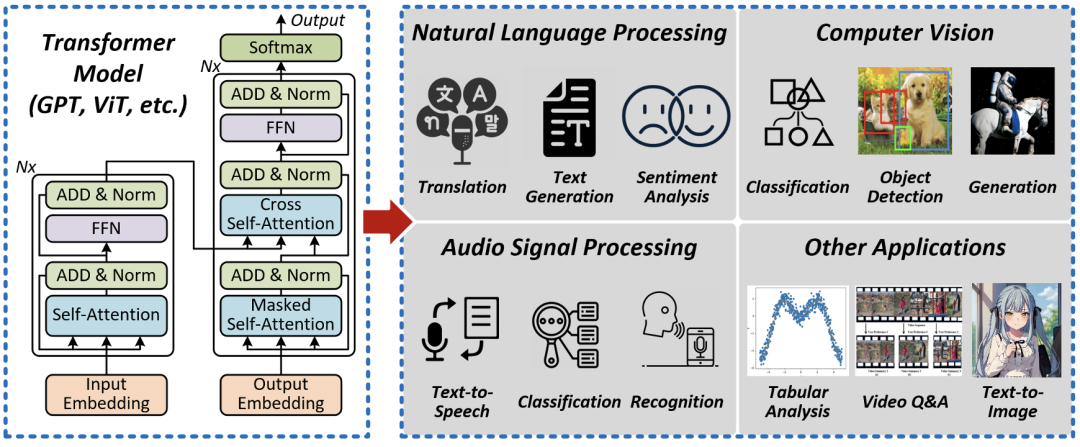
The Transformer model based on the attention mechanism has gradually swept various fields of artificial intelligence since its introduction in 2017, including language modeling, generation, image classification, segmentation, and more. Researchers have found that Transformer models typically exhibit very high accuracy or modeling capability, achieving strong task performance supported by large datasets. Well-known examples of successful Transformer models include GPT, LLAMA, OPT, and the newly proposed video generation model Sora. The powerful performance of Transformers can be attributed to their unique attention mechanism—attention mechanism. It calculates the correlation between any two sets of data in the input and weights the computation process accordingly. For instance, in image tasks, it computes the correlation between any two pixel blocks, while in language tasks, it calculates the correlation between any two words. With the influence of this attention mechanism, Transformer models can achieve very high accuracy at the cost of increased computation and parameter size, such as being difficult to overfit and capable of training on large datasets. However, this leads to a surge in computational load and model scale, posing challenges and obstacles to the use of Transformer models.
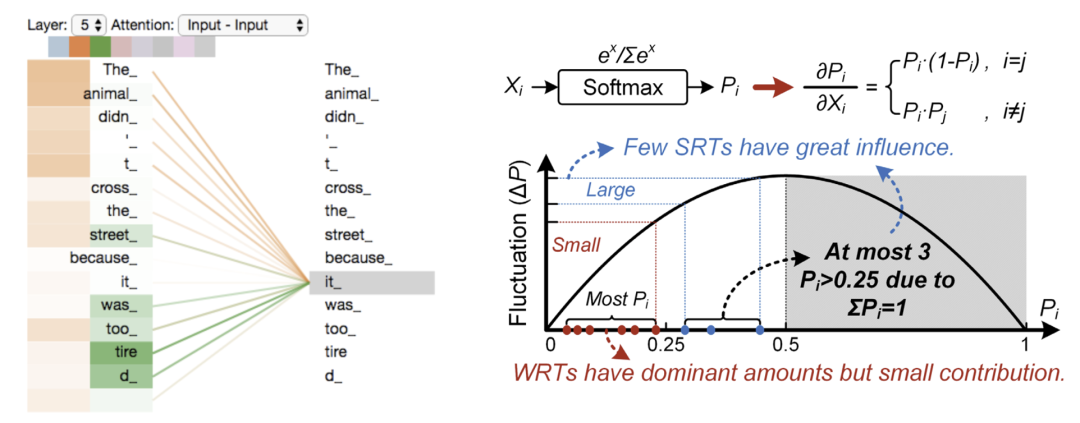
Within attention computation, there exists a special matrix: attention score matrix, which is obtained from the product of the query and key matrices after applying the softmax operation. Since the output of softmax is a probability distribution, meaning all data lies between 0 and 1 and sums to 1, there are many very small scores in the attention score matrix that are very close to 0. Furthermore, based on the error characteristics of the softmax function, it can be deduced that these scores have a high error tolerance, which provides a possibility for optimizing the computation of attention models.
2. Optimization Design of Attention Operators
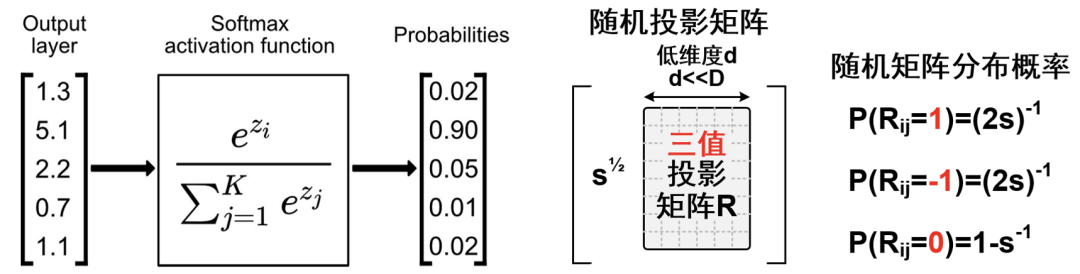
When processing long sequence inputs, the attention operator becomes a computational bottleneck due to its characteristic of having computational load that grows quadratically with input size. To address this, we propose an optimization method based on random projection. The random projection algorithm can perform dimensionality reduction on matrices while preserving the distance characteristics between vectors. This feature aligns well with the requirement to predict attention scores. Additionally, research has shown that attention prediction focuses only on the relative size relationship of values, leading us to propose a prediction method that uses a three-valued sparse random matrix as the projection matrix. By approximating the query and key matrices to predict the attention matrix and using its top-k results as a guide for sparse attention computation, we can significantly reduce the computational demand for attention scores.
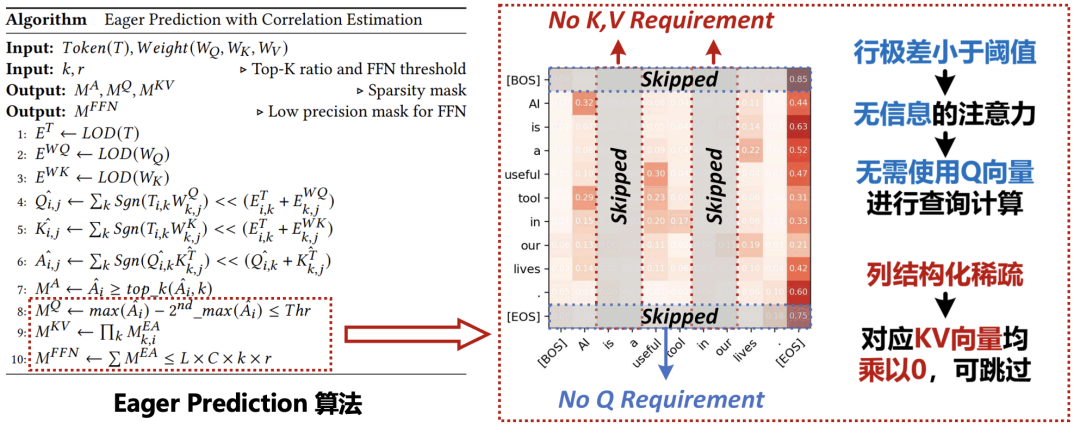
3. Optimization Design of Attention Layers
In processing many common tasks, the computational load of the attention operator is far less than that of the QKV linear layer and FFN linear layer. To achieve effective model acceleration, it is necessary to consider a computation scheme that optimizes the linear layer based on the characteristics of the attention operator. To this end, we propose the Eager Prediction detection algorithm. Its goal is to complete the prediction of attention scores as early as possible, even before the computation of the QKV linear layer begins. The EP algorithm is divided into two parts: the prediction branch and the computation branch. It takes the input token embedding of a layer and the linear weight generated by QK as input. First, it approximates the generated Q and K matrices, then uses this result to estimate the attention matrix, and through topk and threshold operations, derives the sparse computation mask. In the third step, using the obtained mask, it deduces the computation optimization configuration for the QKV linear layer and FFN linear layer both forwards and backwards. Finally, it executes the optimized computation for the entire layer. For the FFN layer after the attention layer, the EP algorithm proposes a dynamic precision adjustment computation scheme. Intuitively, the sparsity of the attention layer reflects the tokens that this layer focuses on. EP counts the tokens that need to be computed after sparsification, finds the important tokens based on a threshold, and performs full-precision FFN computation only for those important tokens, while the rest are computed using MSB. This method can adaptively allocate computation precision for each transformer layer based on its attention, significantly reducing the computational load of low-contribution calculations.
03. Recommended Reading
[1] Y. Qin, et al., “FACT: FFN-Attention Co-optimized Transformer Architecture with Eager Correlation Prediction.” In Proceedings of the 50th Annual International Symposium on Computer Architecture (ISCA`23). Association for Computing Machinery, New York, NY, USA, Article 22, 1–14, doi:10.1145/3579371.3589057
[2] Y. Qin et al., ” A 28nm 49.7TOPS/W Sparse Transformer Processor with Random-Projection-Based Speculation, Multi-Stationary Dataflow, and Redundant Partial Product Elimination.” 2023 IEEE Asian Solid-State Circuits Conference (A-SSCC), Hainan, China, 2023
[3] Y. Wang, et al., “A 28nm 77.35TOPS/W Similar Vectors Traceable Transformer Processor with Principal-Component-Prior Speculating and Dynamic Bit-wise Stationary Computing,” 2023 IEEE Symposium on VLSI Technology and Circuits (VLSI Technology and Circuits), Kyoto, Japan, 2023, pp. 1-2, doi:10.23919/VLSITechnologyandCir57934.2023.10185403.
[4] Y. Wang, et al., “A 28nm 276.55TFLOPS/W Sparse Deep-Neural-Network Training Processor with Implicit Redundancy Speculation and Batch Normalization Reformulation,” 2021 Symposium on VLSI Circuits, Kyoto, Japan, 2021, pp. 1-2, doi: 10.23919/VLSICircuits52068.2021.9492420.
[5] T. J. Ham, Y. Lee, S. H. Seo, S. Kim, H. Choi, S. J. Jung, and J. W. Lee, “Elsa: Hardware-software co-design for efficient, lightweight self-attention mechanism in neural networks,” in 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture (ISCA), pp. 692–705, 2021.
[6] L. Lu, Y. Jin, H. Bi, Z. Luo, P. Li, T. Wang, and Y. Liang, “Sanger: A co-design framework for enabling sparse attention using reconfigurable architecture,” in MICRO-54: 54th Annual IEEE/ACM International Symposium on Microarchitecture, MICRO ’21, (New York, NY, USA), p. 977–991, Association for Computing Machinery, 2021.
[7] Z. Qu, L. Liu, F. Tu, Z. Chen, Y. Ding, and Y. Xie, “Dota: Detect and omit weak attentions for scalable transformer acceleration,” in Proceedings of the 27th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS ’22, (New York, NY, USA), p. 14–26, Association for Computing Machinery, 2022.
[8] H. Wang, Z. Zhang, and S. Han, “Spatten: Efficient sparse attention architecture with cascade token and head pruning,” in IEEE International Symposium on High-Performance Computer Architecture, HPCA 2021, Seoul, South Korea, February 27 – March 3, 2021, pp. 97–110, IEEE, 2021.
04. Highlights of Q&A
Q1: Can the optimization techniques mentioned earlier be applied to the video generation model Sora?
A1: Currently, the Sora model has not been open-sourced, so we cannot provide a definitive conclusion on whether the optimization strategies mentioned in the report can be used as optimizations for Sora. However, it is generally believed that Sora is developed based on the DiT model, which is a Transformer model that projects the input into Latent Space first, computes the output Latent through a structure similar to ViT, and finally obtains the output through a VAE Decoder. This process is very similar to how ViT performs image tasks, so we believe the proposed methods should be feasible. Additionally, Sora is a diffusion model that performs iterative computations during inference, gradually denoising. A DiT will undergo dozens or hundreds of runs to achieve the final generation result, and whether there is further optimization space in this process needs further exploration.
Q2: Will using sparse optimization methods affect the model’s accuracy?
A2: Yes. We have considered the loss of accuracy in our optimization effect tests. For different sparsity configurations, there will be different acceleration effects and accuracy losses. In our experiments, we set a 1% accuracy loss limit for most tasks. By simulating in Pytorch, we retained sparse configurations within the allowable range of accuracy loss and obtained acceleration experimental results based on this.
Q3: Does the proposed hardware architecture design need to support fine-tuning?
A3: Our architecture is designed for high-efficiency inference and does not need to support fine-tuning. It only needs to compute according to the models and computation graphs optimized through the proposed hardware-software co-optimization. However, since some methods may introduce computational losses, such as sparse attention matrices or skipping unnecessary linear layer computations, this may introduce accuracy loss in the model. We compensated for this using hardware-aware fine-tuning on the GPU. The resulting model can conform to the optimized sparse computation flow and can be deployed on our proposed computational architecture for high-efficiency inference.
05. Review Video
