
Source: DeepHub IMBA
This article is about 4000 words long and is recommended to be read in over 10 minutes.
This article will delve into KL divergence and other important divergence concepts.
In the fields of information theory, machine learning, and statistics, KL divergence (Kullback-Leibler divergence) serves as a fundamental concept, playing a key role in quantifying the differences between probability distributions. It is commonly used to measure the information loss when one probability distribution is used to approximate another. This article will delve into KL divergence and other important related divergence concepts.

KL Divergence
KL divergence, also known as relative entropy, is an effective way to measure the difference between two probability distributions P and Q. Its mathematical expression is as follows:
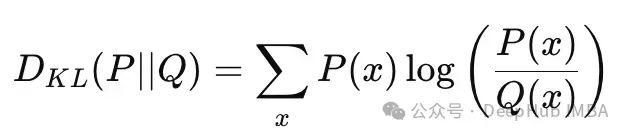
The KL divergence between discrete distributions P(x) and Q(x):
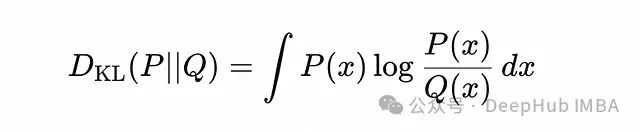
The KL divergence between continuous distributions P(x) and Q(x).
These equations compare the true distribution P with the approximate distribution Q. In practical applications, KL divergence can be understood as the additional coding cost incurred when using a coding system optimized for distribution Q to compress data from distribution P. If Q is close to P, the KL divergence value is small, indicating less information loss; conversely, if Q and P differ significantly, the KL divergence value is large, indicating more information loss. In other words, KL divergence quantifies the additional number of bits required to encode data from the P distribution using a coding scheme designed for Q.
The Relationship Between KL Divergence and Shannon Entropy
To deeply understand KL divergence, it is crucial to relate it to the concept of entropy. Entropy is a measure of the uncertainty or randomness of a distribution. The definition of Shannon entropy is as follows:
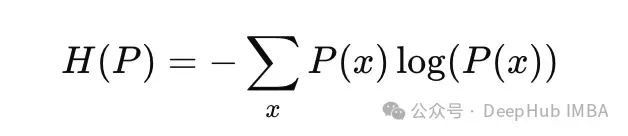
Shannon Entropy of Distribution P(x)
Entropy is a measure of uncertainty, where a lower value indicates a higher certainty about the outcome, meaning more information is possessed. In the binary case, when the probability p=0.5, entropy reaches its maximum, representing maximum uncertainty.
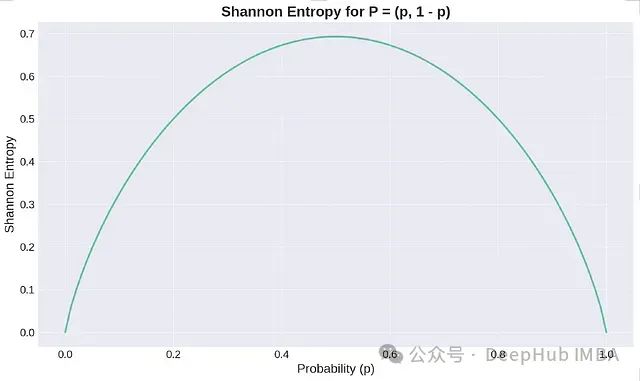
Shannon entropy graph (logarithm base e, can also use base 2).
KL divergence can be viewed as the difference between the entropy of P and the “cross-entropy” between P and Q. Therefore, KL divergence actually measures the additional uncertainty introduced by using Q instead of P.
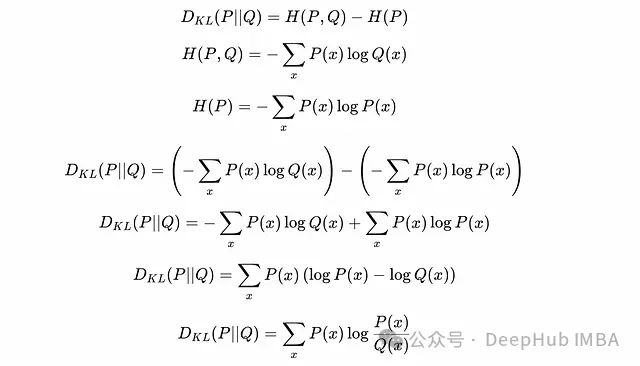
Deriving KL divergence from entropy.
Key Properties of KL Divergence
Non-negativity: KL divergence is always greater than or equal to zero.
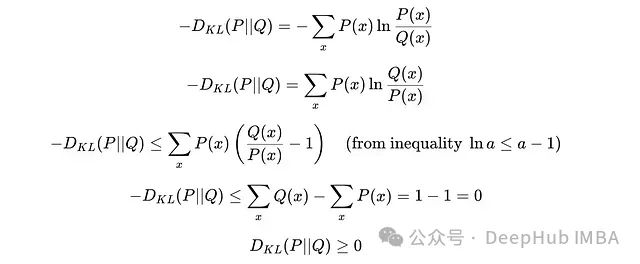
Proof of Non-negativity
Asymmetry: Unlike many distance metrics, KL divergence is asymmetric.
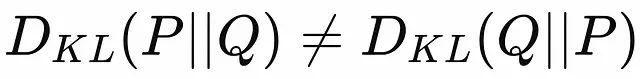
Asymmetry of KL Divergence
Applications of KL Divergence
- Variational Autoencoders (VAE): In VAE, KL divergence acts as a regularizer, ensuring that the latent variable distribution is close to the prior distribution (usually a standard Gaussian distribution).
- Data Compression: KL divergence quantifies the efficiency loss when using one probability distribution to compress data from another distribution, which is extremely useful in designing and analyzing data compression algorithms.
- Reinforcement Learning: In reinforcement learning, such as the Proximal Policy Optimization (PPO) algorithm, KL divergence is used to control the degree of deviation between the new policy and the old policy.
-
Data Drift Detection: In industrial applications, KL divergence is widely used to detect changes in data distribution over time.
Jensen-Shannon Divergence
Jensen-Shannon divergence (JS divergence) is a symmetric divergence measure used to quantify the similarity between two probability distributions. It is built on KL divergence but overcomes the asymmetry limitations of KL divergence. Given two probability distributions P and Q, JS divergence is defined as follows:
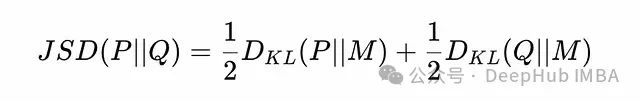
Jensen-Shannon Divergence
Where M is the average (or mixed) distribution of P and Q:
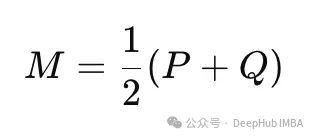
Mixed Distribution
The first term of JS divergence measures the information loss when M is used to approximate P, while the second term measures the information loss when M approximates Q. By calculating the average of the two KL divergences relative to the average distribution M, JS divergence provides a more balanced method for comparing distributions.
This method addresses the asymmetry issue in KL divergence when comparing distributions. JS divergence does not treat P or Q as the “standard” distribution but evaluates their combined behavior through the mixed distribution M. This makes JS divergence particularly useful in scenarios where unbiased comparison of distributions is required.
Renyi Entropy and Renyi Divergence
Renyi entropy is a generalization of Shannon entropy, providing us with a more flexible way to measure the uncertainty of a distribution. The Renyi entropy of a distribution is defined as:
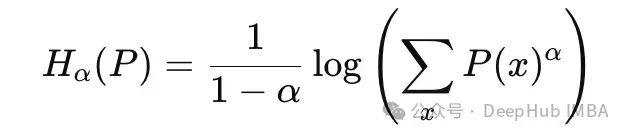
The Renyi entropy of distribution P(x), parameterized by α.
Renyi entropy is controlled by the parameter α > 0, which determines the weight distribution among different probabilities in the distribution.
When α = 1, Renyi entropy is equivalent to Shannon entropy, giving equal weight to all possible events. This can be proven through limits and L’Hôpital’s rule:
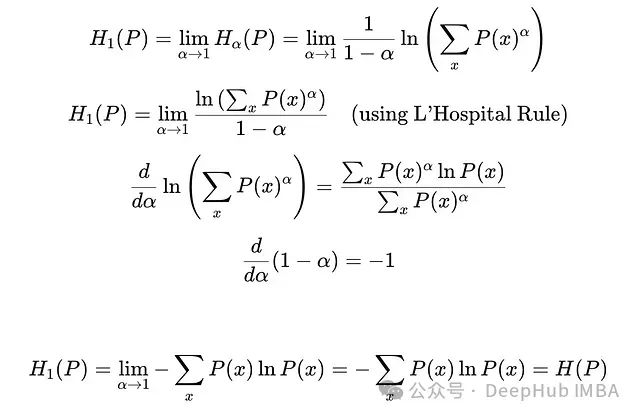
Deriving Shannon Entropy from Renyi Entropy
When α < 1, the entropy calculation is more sensitive to low-probability events (rare events), focusing more on the diversity or dispersion of the distribution.
When α > 1, the entropy calculation is more sensitive to high-probability events, focusing more on the concentration or dominant events of the distribution.
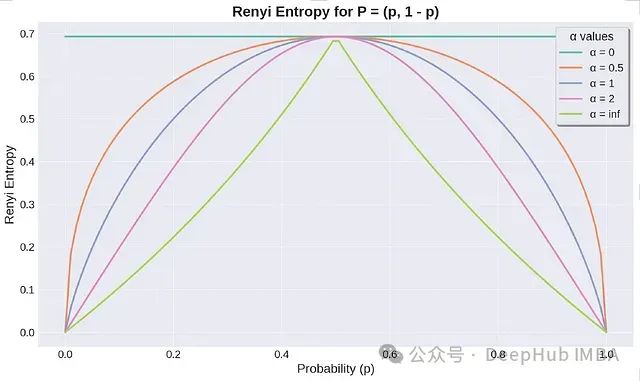
The Renyi entropy graph for different α values (logarithm base e, can also use base 2).
When α = 0, Renyi entropy approaches the logarithm of the number of possible outcomes (assuming all outcome probabilities are non-zero), which is known as Hartley entropy.
When α → ∞, Renyi entropy becomes the minimum entropy, focusing only on the most likely outcomes:
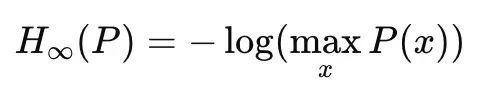
Minimum Entropy
Based on Renyi entropy, we can define Renyi divergence, which is a generalization of KL divergence. The Renyi divergence between two distributions P and Q, parameterized by α, is defined as follows:
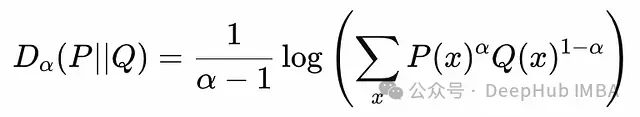
The Renyi divergence between two discrete distributions P(x) and Q(x), parameterized by α.
KL divergence is a special case of Renyi divergence when α = 1:
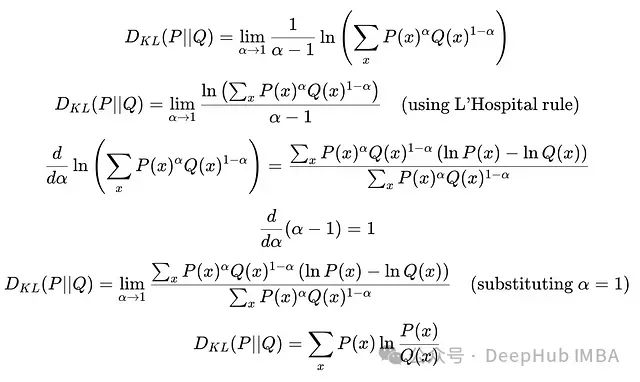
Deriving KL Divergence from Renyi Divergence
The properties of Renyi divergence change with the value of α:
When α < 1, the divergence calculation is more focused on rare events, being more sensitive to the tails of the distribution.
When α > 1, the divergence calculation focuses more on common events, being more sensitive to high-probability areas.
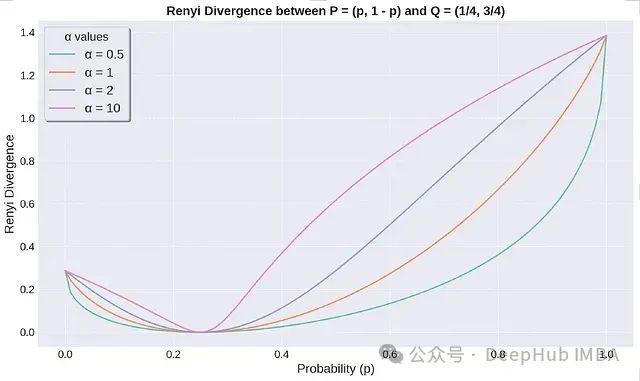
Graph of Renyi divergence between P and Q.
Renyi divergence is always non-negative and equals zero if and only if P = Q. The above graph shows how the divergence changes when distribution P changes. The divergence increases with the value of α, with higher α values making Renyi divergence more sensitive to changes in probability distributions.
Applications of Renyi Divergence
Renyi divergence has found significant applications in the field of Differential Privacy, a key concept in privacy-preserving machine learning. Differential privacy provides a mathematical framework to ensure the privacy of individual data points in a dataset. It ensures that the output of an algorithm does not change significantly due to the presence or absence of a single data point.
Renyi Differential Privacy (RDP) is an extension of differential privacy that utilizes Renyi divergence to provide more precise privacy guarantees. This method is particularly useful in scenarios where finer-grained privacy control is needed.
Case Study: Detecting Data Drift in E-Commerce
In the e-commerce sector, the underlying probability distributions of user behavior may change over time, leading to data drift. This drift can affect various business aspects such as product recommendations. Below, we will demonstrate how to use different divergence metrics to detect this drift through a simplified example.
Consider an e-commerce platform that tracks customer purchasing behavior across five product categories: electronics, clothing, books, home & kitchen, and toys. The platform collects click-through rate data for each category weekly, represented as probability distributions. Here are the data for seven consecutive weeks:
weeks = { 'Week 1': np.array([0.3, 0.4, 0.2, 0.05, 0.05]), 'Week 2': np.array([0.25, 0.45, 0.2, 0.05, 0.05]), 'Week 3': np.array([0.2, 0.5, 0.2, 0.05, 0.05]), 'Week 4': np.array([0.15, 0.55, 0.2, 0.05, 0.05]), 'Week 5': np.array([0.1, 0.6, 0.2, 0.05, 0.05]), 'Week 6': np.array([0.1, 0.55, 0.25, 0.05, 0.05]), 'Week 7': np.array([0.05, 0.65, 0.25, 0.025, 0.025]), }
The data analysis shows the following trends:
- From Week 1 to Week 2: A slight drift is observed, with a slight increase in the click-through rate of the second category (clothing).
- Week 3: A more pronounced drift occurs, further enhancing the dominance of the clothing category.
-
From Week 5 to Week 7: Significant changes occur, with the clothing category continuing to increase its click share, while other categories, especially electronics, see a relative decline in importance.
To quantify these changes, we can implement the following divergence calculation functions:
# KL divergence calculation def kl_divergence(p, q): return np.sum(kl_div(p, q))
# Jensen-Shannon divergence calculation def js_divergence(p, q): m = 0.5 * (p + q) return 0.5 * (kl_divergence(p, m) + kl_divergence(q, m))
# Renyi divergence calculation def renyi_divergence(p, q, alpha): return (1 / (alpha - 1)) * np.log(np.sum(np.power(p, alpha) * np.power(q, 1 - alpha)))
Using these functions, we can calculate and plot the changes in different divergences over time: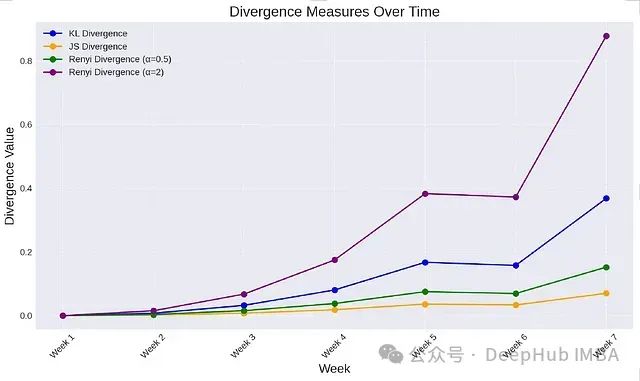
Divergence measurements over time.
Results Analysis
- KL Divergence: Shows an upward trend over time, indicating that the purchasing distribution is gradually deviating from the initial baseline. The increase in KL divergence from Week 1 to Week 7 highlights the continued dominance of the second category (clothing).
- Jensen-Shannon Divergence: Exhibits a similar steady upward trend, further confirming the gradual changes in the distribution. JS divergence captures the overall drift across categories.
- Renyi Divergence: Shows different patterns of change based on the selected α value:
- When α = 0.5: The divergence is more sensitive to rare categories (such as home & kitchen, toys). It can capture drift earlier when fluctuations occur in these categories (especially from Week 6 to Week 7, when their probabilities drop to 0.025).
-
When α = 2: The divergence highlights the continued growth of the clothing category, reflecting changes in high-probability events and indicating that the distribution is becoming more concentrated.
Application Value
By continuously monitoring these divergence metrics, e-commerce platforms can:
- Timely detect changes in user behavior patterns.
- Adjust business strategies based on detected drifts, such as retraining recommendation systems.
-
Conduct in-depth analysis of potential factors leading to drift, such as seasonal trends or the impact of marketing activities.
This case illustrates how theoretical concepts can be applied to real business scenarios, highlighting the unique advantages of different divergence metrics in capturing changes in data distribution. By comprehensively utilizing these tools, businesses can better grasp market dynamics and make data-driven decisions.
Conclusion
This article has explored several core concepts in information theory, machine learning, and statistics: entropy, KL divergence, Jensen-Shannon divergence, and Renyi divergence. These concepts are not only the foundation of theoretical research but also important tools in modern data analysis and machine learning applications.
Entropy, as a foundation of information theory, provides us with a mathematical framework for quantifying information and uncertainty. Various divergence measures further extend this concept, allowing us to compare and analyze different probability distributions. KL divergence, with its unique properties in measuring distribution differences, plays a key role in areas such as variational inference and model compression. Jensen-Shannon divergence, through its symmetric property, provides us with a more balanced method for comparing distributions, especially suitable for scenarios requiring unbiased comparisons. Renyi divergence, with its adjustable parameter α, offers a series of flexible divergence measures that can focus on different aspects of distributions based on specific needs.
The practical value of these theoretical concepts cannot be ignored. As seen in the case of detecting data drift in e-commerce, these divergence metrics can effectively capture changes in data distribution over time. This is not limited to e-commerce; these concepts have wide applications in various fields such as financial risk assessment, bioinformatics, and natural language processing.
As we move deeper into the era of big data and the continuous advancement of artificial intelligence technologies, precise analysis and comparison of data distributions become increasingly important. Entropy and various divergence metrics provide us with powerful tools to extract valuable information from massive datasets, identify potential patterns and trends, and make data-driven decisions.
Looking ahead, these concepts are likely to find applications in more emerging fields, such as information processing in quantum computing and complex network analysis. At the same time, researchers are continuously exploring new variants and extensions of these concepts to address increasingly complex data analysis challenges.
In summary, entropy, KL divergence, JS divergence, and Renyi divergence are not only important topics in theoretical research but also serve as a bridge connecting abstract mathematical concepts with practical data analysis. Mastering these tools will enable us to gain a deeper understanding and analysis of complex data worlds, providing strong support for scientific research and technological innovation.
Author: Saankhya Mondal
Editor: Huang Jiyan
About Us
Data派THU, as a public account focused on data science, is backed by Tsinghua University’s Big Data Research Center, sharing cutting-edge data science and big data technology innovation research dynamics, continuously disseminating data science knowledge, and striving to build a platform for gathering data talent, creating the strongest group in China’s big data.

Sina Weibo: @数据派THU
WeChat Video Account: 数据派THU
Today’s Headlines: 数据派THU
