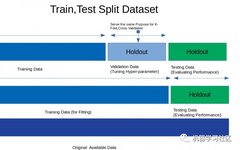
Explaining 7 Cross-Validation Methods in Machine Learning

Source: Machine Learning Community, Data Science THU

During the model building phase of any supervised machine learning project, the goal of training the model is to learn the best values for weights and biases from labeled examples.

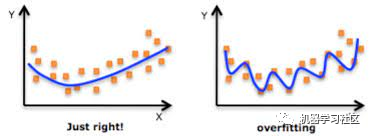
If we use the same labeled examples to test our model, it will be a methodological error because a model that only repeats the labels of the samples it just saw would achieve perfect scores but would not be able to predict anything useful – future data, a situation known as overfitting.

To overcome the problem of overfitting, we use cross-validation. So you need to know what cross-validation is? And how does it solve the problem of overfitting?

What is Cross-Validation?

Cross-validation is a statistical method used to estimate the performance of machine learning models. It is a way to evaluate how the results of statistical analyses generalize to an independent data set.

How Does It Solve the Problem of Overfitting?

In cross-validation, we generate multiple small training-test splits from the training data and use these splits to tune your model. For example, in standard k-fold cross-validation, we divide the data into k subsets. Then, we iterate the training algorithm on k-1 subsets while using the remaining subset as the test set. This way, we can test our model on data that was not involved in the training.In this article, I will share 7 of the most commonly used cross-validation techniques and their pros and cons. I also provide code snippets for each technique, welcome to bookmark and learn, and please like to support.Below are these techniques:

HoldOut Cross-Validation
K-Fold Cross-Validation
Stratified K-Fold Cross-Validation
Leave P Out Cross-Validation
Leave One Out Cross-Validation
Monte Carlo (Shuffle-Split)
Time Series (Rolling Cross-Validation)

1. HoldOut Cross-Validation

In this cross-validation technique, the entire dataset is randomly divided into a training set and a validation set. Empirically, about 70% of the entire dataset is used as the training set, and the remaining 30% is used as the validation set.

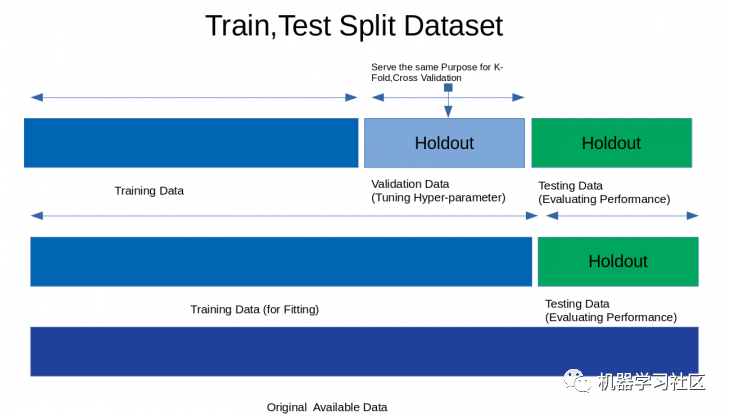
Advantages:1. Fast execution: Because we only need to split the dataset into a training set and a validation set once, and the model will only be built once on the training set, it can be executed quickly.Disadvantages:1. Not suitable for imbalanced datasets: Suppose we have an imbalanced dataset with class “0” and class “1”. If 80% of the data belongs to class “0” and the remaining 20% belongs to class “1”, during the training-test split with a training set size of 80% and a test data size of 20%, it may happen that all 80% of class “0” data is in the training set while all data of class “1” is in the test set. Thus, our model cannot generalize well to our test data because it has not seen any data from class “1” before;2. A significant amount of data cannot train the model.In the case of small datasets, retaining a portion for testing the model may miss important features that our model could have learned from that data.Code Snippet:

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
iris=load_iris()
X=iris.data
Y=iris.target
print("Size of Dataset {}".format(len(X)))
logreg=LogisticRegression()
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.3,random_state=42)
logreg.fit(x_train,y_train)
predict=logreg.predict(x_test)
print("Accuracy score on training set is {}".format(accuracy_score(logreg.predict(x_train),y_train)))
print("Accuracy score on test set is {}".format(accuracy_score(predict,y_test)))

Explaining 7 Cross-Validation Methods in Machine Learning

2. K-Fold Cross-Validation

In this K-fold cross-validation technique, the entire dataset is divided into K equal-sized parts. Each partition is called a “fold”. Therefore, since we have K parts, we call it K-fold. One fold is used as a validation set, and the remaining K-1 folds are used as the training set.This technique repeats K times until each fold has been used as a validation set and the remaining folds as the training set.The final accuracy of the model is calculated by averaging the accuracy of k models on the validation data.

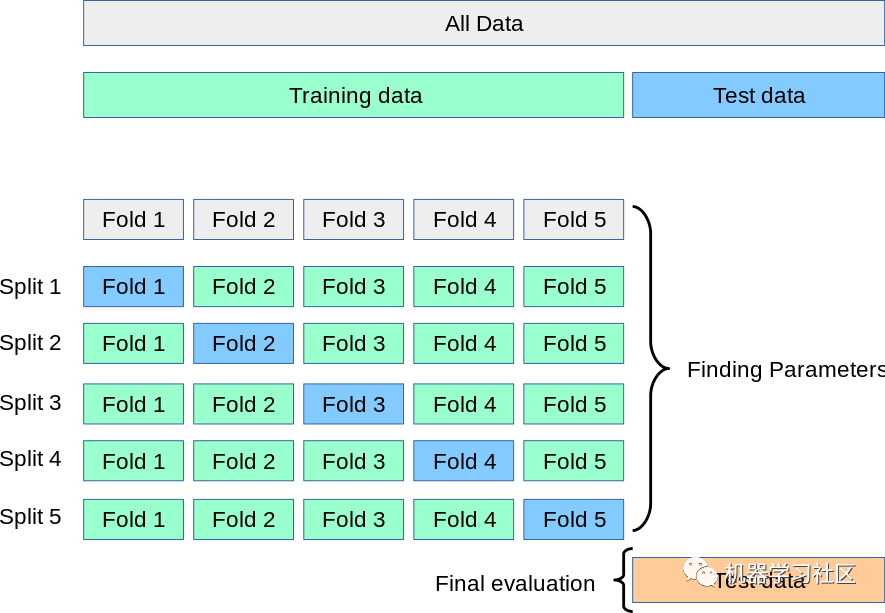
Advantages:1. The entire dataset is used as both the training set and the validation set.Disadvantages:1. Not for imbalanced datasets: As discussed in the HoldOut cross-validation case, it can also happen in K-Fold validation that all samples in the training set do not have samples of class “1”, only class “0”. The validation set will have a sample of class “1”;2. Not suitable for time series data: For time series data, the order of samples is important. However, in K-fold cross-validation, samples are selected in random order.Code Snippet:

from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score,KFold
from sklearn.linear_model import LogisticRegression
iris=load_iris()
X=iris.data
Y=iris.target
logreg=LogisticRegression()
kf=KFold(n_splits=5)
score=cross_val_score(logreg,X,Y,cv=kf)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))

3. Stratified K-Fold Cross-Validation

Stratified K-Fold is an enhanced version of K-Fold cross-validation, primarily used for imbalanced datasets. Like K-fold, the entire dataset is divided into K folds of equal size.However, in this technique, each fold will have the same ratio of target variable instances as in the entire dataset.

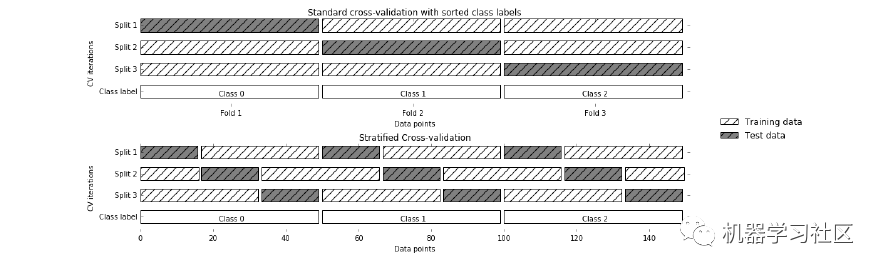
Advantages:1. Very effective for imbalanced data: Each fold in stratified cross-validation will represent all classes of data at the same ratio as in the entire dataset.Disadvantages:1. Not suitable for time series data: For time series data, the order of samples is important. However, in stratified cross-validation, samples are selected in random order.Code Snippet:

from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score,StratifiedKFold
from sklearn.linear_model import LogisticRegression
iris=load_iris()
X=iris.data
Y=iris.target
logreg=LogisticRegression()
stratifiedkf=StratifiedKFold(n_splits=5)
score=cross_val_score(logreg,X,Y,cv=stratifiedkf)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))

4. Leave P Out Cross-Validation

Leave P Out cross-validation is an exhaustive cross-validation technique where p samples are used as the validation set, and the remaining n-p samples are used as the training set.Assuming we have 100 samples in the dataset. If we use p=10, then in each iteration, 10 values will be used as the validation set, while the remaining 90 samples will be used as the training set.This process repeats until the entire dataset is partitioned into p samples and n-p training samples for the validation set.Advantages:1. All data samples are used as training and validation samples.Disadvantages:1. Long computation time: Since the above technique continuously repeats until all samples are used as the validation set, the computation time will be longer;2. Not suitable for imbalanced datasets: Similar to K-fold cross-validation, if we only have samples of one class in the training set, our model will not generalize to the validation set.Code Snippet:

from sklearn.model_selection import LeavePOut,cross_val_score
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
iris=load_iris()
X=iris.data
Y=iris.target
lpo=LeavePOut(p=2)
lpo.get_n_splits(X)
tree=RandomForestClassifier(n_estimators=10,max_depth=5,n_jobs=-1)
score=cross_val_score(tree,X,Y,cv=lpo)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))

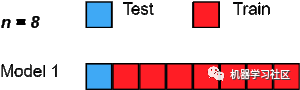
5. Leave One Out Cross-Validation

Leave One Out cross-validation is an exhaustive cross-validation technique where 1 sample point is used as the validation set, and the remaining n-1 samples are used as the training set.Assuming we have 100 samples in the dataset. Then in each iteration, 1 value will be used as the validation set, while the remaining 99 samples are used as the training set. Thus, this process repeats until each sample in the dataset has been used as a validation point.It is the same as using p=1 in LeavePOut cross-validation.

Code Snippet:

from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import LeaveOneOut,cross_val_score
iris=load_iris()
X=iris.data
Y=iris.target
loo=LeaveOneOut()
tree=RandomForestClassifier(n_estimators=10,max_depth=5,n_jobs=-1)
score=cross_val_score(tree,X,Y,cv=loo)
print("Cross Validation Scores are {}".format(score))
print("Average Cross Validation score :{}".format(score.mean()))

6. Monte Carlo Cross-Validation (Shuffle Split)

Monte Carlo cross-validation, also known as Shuffle Split cross-validation, is a very flexible cross-validation strategy. In this technique, the dataset is randomly divided into training and validation sets.We have already decided the percentage of the dataset to be used as the training set and the percentage to be used as the validation set. If the sum of the percentages of the training and validation set sizes is not 100, the remaining dataset will not be used for the training or validation set.Assuming we have 100 samples, where 60% of the samples are used as the training set and 20% of the samples are used as the validation set, then the remaining 20% (100-(60+20)) will not be used.This split will be repeated as many times as we specify.

Advantages:1. We can freely use the size of the training and validation sets;2. We can choose the number of repetitions without relying on the number of folds.Disadvantages:1. May not select very few samples for the training or validation sets;2. Not suitable for imbalanced datasets: Once we define the sizes of the training and validation sets, all samples are randomly selected, so the training set may not include data categories present in the test set, and the model will not generalize to unseen data.Code Snippet:

from sklearn.model_selection import ShuffleSplit,cross_val_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
logreg=LogisticRegression()
shuffle_split=ShuffleSplit(test_size=0.3,train_size=0.5,n_splits=10)
scores=cross_val_score(logreg,iris.data,iris.target,cv=shuffle_split)
print("cross Validation scores:n {}".format(scores))
print("Average Cross Validation score :{}".format(scores.mean()))

7. Time Series Cross-Validation

What is Time Series Data?Time series data is data collected at different time points. Since data points are collected in adjacent time periods, there may be correlations between observations. This is one of the distinguishing features of time series data from cross-sectional data.How to Perform Cross-Validation for Time Series Data?In the case of time series data, we cannot choose random samples and assign them to the training or validation sets because it makes no sense to use values from future data to predict values from past data.Since the order of data is crucial for time series-related problems, we split the data into training and validation sets based on time, also known as the “forward chaining” method or rolling cross-validation.We start with a small portion of data as the training set. Based on that set, we predict later data points and check the accuracy.Then the predicted samples are included as part of the next training dataset and predictions are made for subsequent samples.

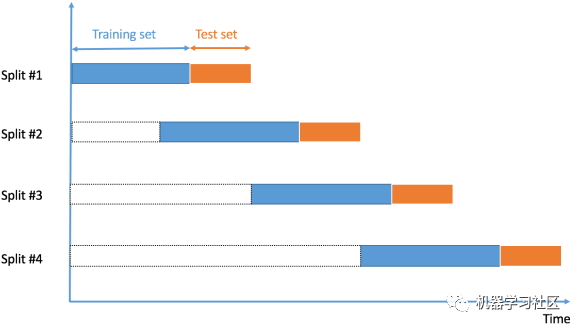
Advantages:1. One of the best techniques.Disadvantages:1. Not suitable for validation of other data types: Like other techniques, we choose random samples as training or validation sets, but in this technique, the order of data is very important.Code Snippet:

import numpy as np
from sklearn.model_selection import TimeSeriesSplit
X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
y = np.array([1, 2, 3, 4, 5, 6])
time_series = TimeSeriesSplit()
print(time_series)
for train_index, test_index in time_series.split(X):
    print("TRAIN:", train_index, "TEST:", test_index)
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

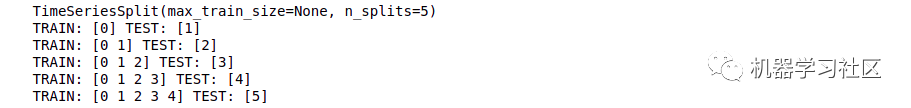
Conclusion

In this article, I tried to outline how various cross-validation techniques work and what we should keep in mind when implementing these techniques. I sincerely hope this helps you on your data science journey.

For reference links, click the bottom left corner to read the original text. For academic sharing only, if there is any infringement, please delete immediately.

Editor / Garvey

Review / Fan Ruiqiang

Recheck / Fan Ruiqiang

Transmitted from: Mathematics China