Can Light Compute Like the Brain? Photonic Neural Networks

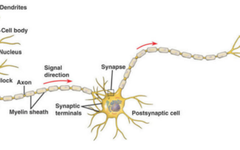
The human brain is a complex network structure composed of approximately 100 billion neurons, each of which is a highly sophisticated cell containing a cell body and an axon, along with many dendrites and synapses. Dendrites extend like branches from the cell body, receiving signals from other neurons. After receiving these signals, they are integrated and processed in the cell body, and when the combined input reaches a certain threshold, the neuron generates a neural impulse. This neural impulse is transmitted via the axon to other neurons or cells. These neurons are interconnected through synapses, forming a vast and complex communication network responsible for processing information, controlling bodily functions, and supporting consciousness and thought activities.

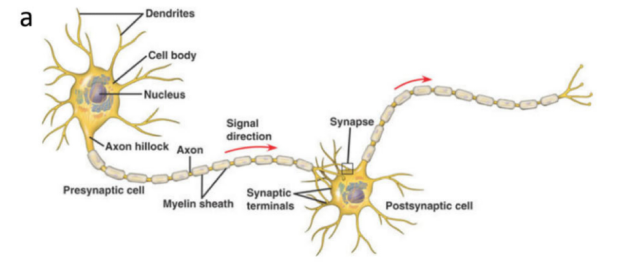
Figure 1 Structure of a Neuron[1]

In 1940, mathematician Warren McCulloch and neurophysiologist Walter Pitts proposed a simple neuron model known as the McCulloch-Pitts model to describe the basic computational functions of neurons. In 1943, they published a paper titled “A Logical Calculus of the Ideas Immanent in Nervous Activity,” which first introduced the concept of neural networks[2], laying the foundation for the field of artificial neural networks. In 1957, psychologist Frank Rosenblatt introduced the perceptron model, a simple and classic neural network model. According to this model, when a perceptron receives a set of inputs, it performs a weighted sum and compares the result with an activation function. If the result exceeds the activation function, it produces an output. This provides a mathematical description of the function of a neuron.

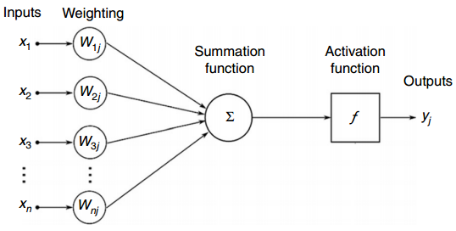
Figure 2 Mathematical Model of a Perceptron

However, the perceptron model has its limitations, yet this foundational design has inspired significant developments in neural networks over time. Later, multilayer perceptrons and more complex activation functions were introduced, and subsequently, the concept of backpropagation was proposed, making multilayer artificial neural networks more complex and better trained to learn more complex content. In summary, neural networks can change the weights of each node through training, allowing the model to produce the desired output for various inputs.

By 2010, with the improvement of computing power and the development of big data, deep learning experienced unprecedented growth. Some deep learning models, such as convolutional neural networks and recurrent neural networks, achieved significant results in fields like image processing and natural language processing. Expanding the scale of deep neural networks enables them to perform more complex tasks; over the past decade, deep neural network models have evolved from 100 million parameters to one trillion parameters[3]. The human brain has about 100 billion neurons, with approximately 1 trillion synapses connecting them[4]. Therefore, constructing larger-scale deep neural networks will be a future development goal, requiring higher computational efficiency and data throughput. Currently, transistor circuits are gradually approaching physical limits in size and quantity. Using electronics for computation leads to a series of issues such as heat generation, bandwidth limitations, and crosstalk due to the intrinsic properties of electrons. These problems restrict the development of electronic deep neural networks. At this point, the concept of optical computing gradually came into view, which has many advantages, such as immense bandwidth, electromagnetic interference resistance, and lossless propagation characteristics. Some devices developed using photonic properties have already replaced electronic devices, such as communication optical fibers. Optical neural networks aim to leverage these properties of photons to achieve lower energy consumption and more efficient neural networks.

Currently, many classic optical neural network structures have been proposed. For example, in 2017, Shen Yichen and others introduced a novel photonic neural network with 56 programmable Mach-Zehnder interferometer elements in their paper “Deep Learning with Coherent Nanophotonic Circuits,” demonstrating vowel recognition[5]. In 2018, Lin Xing and others proposed a diffractive all-optical deep learning structure in their paper “All-optical machine learning using diffractive deep neural networks,” and used a diffraction plate to create this structure, achieving accurate results in handwritten digit recognition and clothing classification tasks[6].

Figure 3 Novel Photonic Neural Network Based on MZI Interferometer

The two optical neural networks mentioned above are constructed based on the principles of interference and diffraction, respectively. We know that interference is a phenomenon caused by the superposition of waves, resulting in a redistribution of intensity, requiring the waves to have the same frequency, parallel vibration components, and stable phase differences. Similarly, the diffraction phenomenon refers to the deviation of light waves from straight-line propagation, where the formation of stable diffraction patterns requires relative stability of wave crests and troughs. Using coherent light sources can achieve the most pronounced interference and diffraction effects. Furthermore, many classical theoretical derivations of interference and diffraction propagation are based on the assumption of coherent light waves, allowing for the formulation of many concise and effective formulas to accurately describe the propagation process of light waves.

Therefore, using a coherent light source can conveniently and effectively perform optical computations or construct optical neural networks. In coherent light, the vibrations of light waves are ordered and coordinated. This means that the phase relationships between peaks and peaks, and troughs and troughs are stable. Lasers are an ideal coherent light source, and the development of photonic neural networks relies on various characteristics of lasers.

Let’s first review the concept of a laser. Laser, also known as LASER (Light Amplification by Stimulated Emission of Radiation), can be referred to as stimulated emission light amplification or sometimes as stimulated emission light oscillation. As the name suggests, it refers to the light amplification caused by stimulated emission.

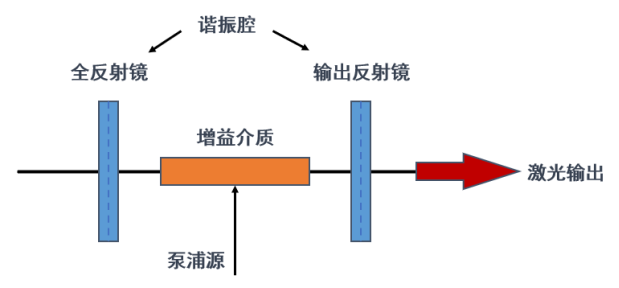
Figure 4 Schematic Diagram of a Laser Structure

So what is “stimulated emission” mentioned multiple times above? Stimulated emission refers to the process in which an atom or molecule, when excited by external light, falls from a high energy level to a low energy level, simultaneously releasing a beam of light with the same frequency and phase as the exciting light. In a laser, a medium (gain medium) absorbs energy (pumping), causing its atoms or molecules to transition from a low energy level to a high energy level, and then through stimulated emission, more photons are generated. These photons have the same frequency and phase as the incident light. Additionally, the laser has two reflective surfaces forming a cavity (resonant cavity), and when these photons repeatedly move back and forth in the cavity, they continuously trigger stimulated emissions, leading to amplification, and finally output from the laser. The light sources we generally use for illumination are incoherent light sources, which rely on spontaneous emission. Spontaneous emission occurs when atoms or molecules fall back from an excited state to a ground state, emitting light randomly, resulting in random phase, frequency, and amplitude, lacking coherence.

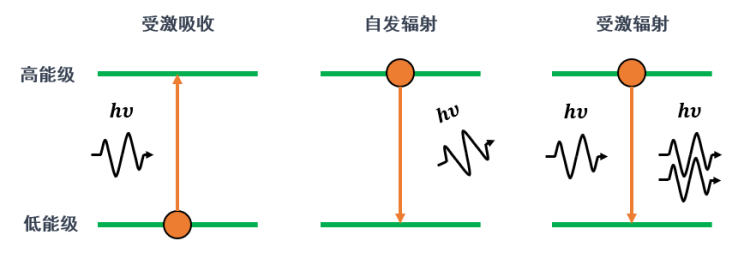
Figure 5 Schematic Diagram of Stimulated Absorption, Spontaneous Emission, and Stimulated Emission

Long ago in the 17th century, the widely accepted theory of light propagation was the particle theory. At that time, an Italian physicist named Grimaldi conducted an experiment using a very small light source to illuminate a small hole on an opaque screen and observed the light intensity on the screen behind it. Because the size of the light source was very small, it avoided the blurring effect caused by the penumbra (for example, the edges of a shadow in sunlight are fuzzy) due to the size of the light source. According to the particle theory, a sharply defined outline should appear on the screen. However, in the experiment, Grimaldi observed that the edges of the image were blurred; he described and summarized this phenomenon, accurately reporting the diffraction phenomenon for the first time. At that time, lasers had not yet been proposed or invented, and the spectra of ordinary light sources were relatively broad, with poor coherence. Today, if we use a laser to repeat his experiment, we would observe distinct diffraction rings on the screen. Thus, a light source with good coherence is also a crucial condition for optical neural network experiments to align with design.

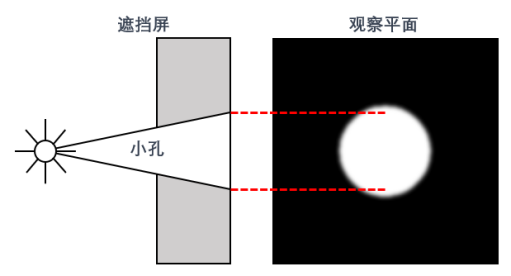
Figure 6 Grimaldi’s Small Hole Experiment

With the conditions of having lasers as coherent light sources, combined with the theory of light propagation, researchers began to find ways to utilize the propagation of light to simulate signal transmission in neural networks, that is, to design the structure of optical neural networks. Next, we will introduce the structure and principles of deep diffractive neural networks.

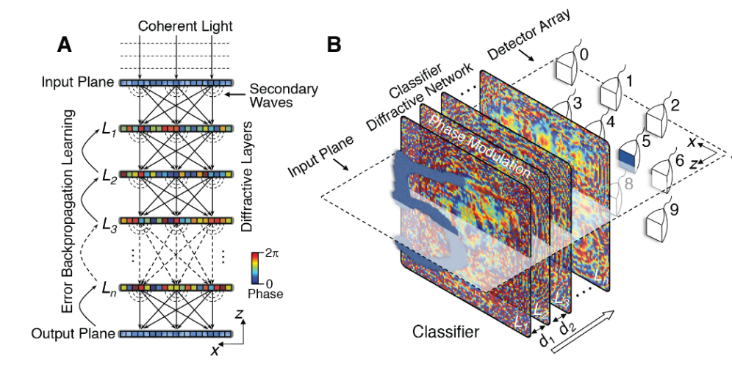
Figure 7 Schematic Diagram of a Deep Diffractive Neural Network

As shown in the figure, the diffractive neural network is a structure composed of many diffraction layers, each of which consists of many “pixels” that can modulate the phase of light waves. The incident light, loaded with input information, enters the diffractive neural network, and as it passes through each “pixel,” it undergoes phase modulation. Upon leaving the pixel, diffraction occurs, and the diffracted light wave is transmitted to the next diffraction layer, where it is modulated by the next layer’s pixels and diffracted again, propagating layer by layer until it reaches the output plane. Therefore, the diffractive neural network follows the principle of coherent superposition of sub-waves and the diffraction equation, mapping the input plane to the output plane in a neural network structure.

Compared to the human neural network, each pixel in the diffractive neural network corresponds to a neuron, responsible for performing weighted summation on the input and outputting to the next neuron. However, if each “pixel” randomly modulates the phase of the light wave, the desired results cannot be achieved for a given light wave input. Therefore, it is necessary to train each “pixel” regarding the degree of modulation it applies to the light wave. Taking the handwritten digit dataset as an example, if we want the diffractive neural network to classify handwritten digits, we first need to input images of the handwritten digits. After passing through the neural network, it produces an output, which is then compared with the ideal output to calculate the error. This error is backpropagated through the neural network, leading to a small update for each “pixel,” which constitutes the training process. Training this neural network with a large amount of data enables it to classify handwritten digits. Even if the input is a digit that the network has not been trained on, it can recognize and classify it.

However, currently, the diffractive neural network cannot complete the entire training process optically. Some steps must be performed on a computer, so accurate modeling of the diffraction process of light is still required in the computer. The diffractive neural network is based on the Fresnel-Huygens principle, which was proposed by Fresnel in 1818 based on previous work. He believed that any point P outside the wavefront is the result of the coherent superposition of infinitely many spherical sub-waves from the wavefront. Later, Kirchhoff used this theory as an idea to derive the Fresnel-Kirchhoff diffraction equation based on the Helmholtz equation derived from Maxwell’s equations combined with Green’s theorem. This equation can accurately describe the diffraction process of light waves in space. Later, Sommerfeld resolved the mathematical inconsistency of Kirchhoff’s diffraction theory and proposed the Rayleigh-Sommerfeld diffraction. In the diffractive neural network, the first kind of Rayleigh-Sommerfeld diffraction integral is used to model the propagation of light waves within the network. By simulating the propagation of light in the diffractive neural network using this mathematical model in a computer and completing backpropagation and pixel weight updates through deep learning frameworks, the neural network can be trained and tested. Finally, when the accuracy of the neural network reaches a certain level, the modulation data of the diffractive layers are saved and processed into diffractive components to form the diffractive neural network. The resulting diffractive neural network can recognize and classify handwritten digits at the speed of light.

It can be said that lasers are a significant invention that has opened the door to modern optical research and applications. The unique characteristics of lasers make them play an unparalleled role in the field of optics, providing unprecedented precision tools in scientific research and having a profound impact across various fields, including medicine, communication, and material processing. Compared to natural light, laser photons are highly coherent, meaning the vibrations of light waves can maintain a high degree of order and coordination. This coherence allows lasers to exhibit remarkable characteristics in phenomena such as interference and diffraction, providing a theoretical and practical foundation for the development of holography and optical information technology. Therefore, lasers have become an essential tool driving in-depth optical research and playing a crucial role in many fields. From fundamental science to practical applications, lasers have become indispensable instruments in the field of optics, bringing unprecedented brightness to humanity.

References:

[1] Mohammed H S. Design and Study of Interactive Systems based on Brain-Computer Interfaces and Augmented Reality[D]. INSA de Rennes, 2019.

[2] McCulloch W S, Pitts W. A logical calculus of the ideas immanent in nervous activity[J]. The bulletin of mathematical biophysics, 1943, 5: 115-133.

[3]:Villalobos P, Sevilla J, Besiroglu T, et al. Machine learning model sizes and the parameter gap[J]. arXiv preprint arXiv:2207.02852, 2022.

[4]:Zhang J. Basic neural units of the brain: neurons, synapses and action potential[J]. arXiv preprint arXiv:1906.01703, 2019.

[5] Shen Y, Harris N C, Skirlo S, et al. Deep learning with coherent nanophotonic circuits[J]. Nature photonics, 2017, 11(7): 441-446.

[6] Lin X, Rivenson Y, Yardimci N T, et al. All-optical machine learning using diffractive deep neural networks[J]. Science, 2018, 361(6406): 1004-1008.