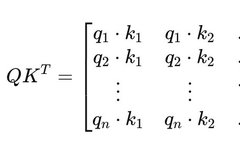Advanced Attention Mechanisms in Transformers for Long Sequences

When handling long sequences, Transformers face challenges such as attention dispersion and increased noise. As the sequence length increases, each token must compete for attention scores with more tokens, which can lead to diluted attention scores. This dilution can result in less concentrated and relevant contextual representations, particularly affecting tokens that are far apart from each other.

Moreover, longer sequences are more likely to contain irrelevant or less relevant information, introducing noise that further disperses the attention mechanism, preventing it from focusing on the important parts of the input.

Therefore, this article focuses on exploring the mathematical complexity and theoretical foundations of advanced attention mechanisms applied to long sequences, which can effectively manage the computational and cognitive challenges posed by long sequences in Transformer models.

Impact of Sequence Length on Attention

To understand how longer sequences dilute attention scores and increase noise, we need to delve into the mathematical principles of the attention mechanisms used in models like Transformers.

The attention mechanism in the Transformer is based on scaled dot-product attention, defined as:

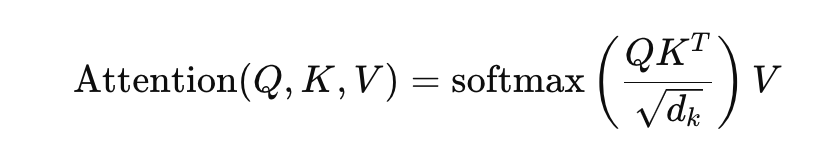
Q (Query), K (Key), and V (Value) are matrices derived from the input embeddings. Dk is the dimensionality of the vectors used to scale the dot product to prevent large values that could destabilize the softmax function.

Consider a simple example where Q and K are the same, and each element is equally relevant:

As n (the sequence length) increases, the sum of each row in the matrix QK^T (before applying softmax) increases because more terms are added, which may lead to a situation where the impact of any single k_j on a given q_i is weakened, as it approaches the average:

As n increases, the denominator grows, dispersing attention across more tokens. This “dilution” reduces the model’s ability to focus on the most relevant items.

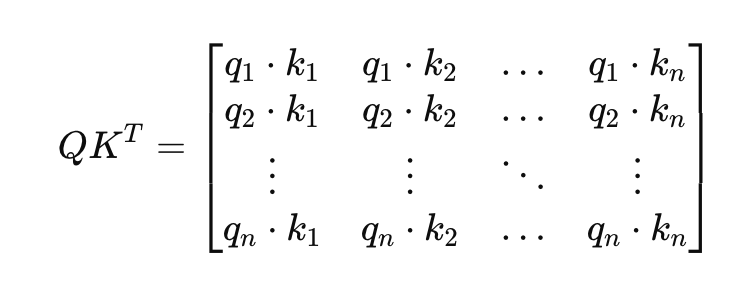
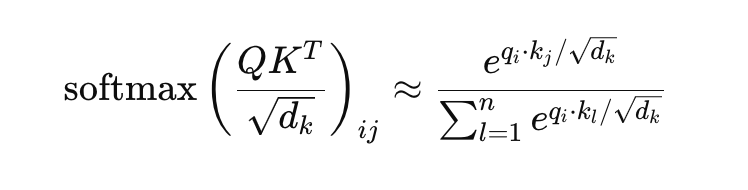
Additionally, longer sequences often contain segments that are less relevant to the current context being processed. These less relevant or “noisy” segments still compute dot products in the attention mechanism:

As n increases, the probability that q_i aligns with several k_j representing noise (or less relevant information) also increases. This noise impacts the softmax function’s ability to effectively prioritize the most relevant items, thereby diminishing the overall quality of attention-driven context understanding.

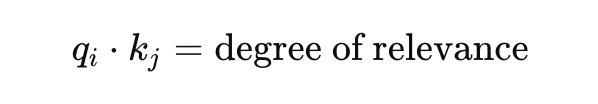
Locality-Sensitive Hashing (LSH)

Reduces computational demands by limiting the number of interactions between tokens. Tokens are hashed into buckets, and attention is only computed within buckets, simplifying the attention matrix.

Each token is projected into a lower-dimensional space defined by a hash function:

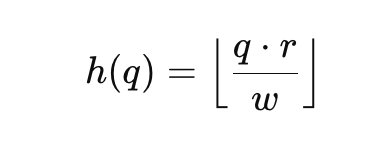
Attention is computed only within buckets:

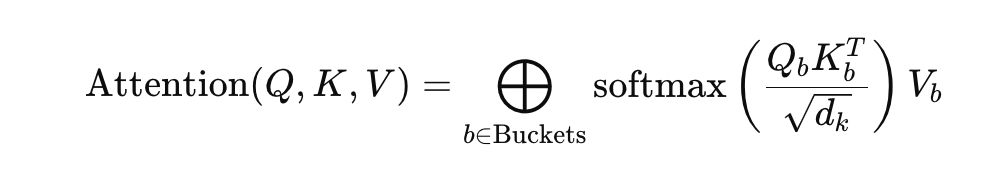
This mechanism selectively concentrates the model’s computational resources, reducing overall complexity from O(n²) to O(n log n).

Low-Rank Attention

Low-rank attention is a method of optimizing the attention mechanism by decomposing the attention matrix into low-rank matrices, effectively simplifying the computational process. Low-rank decomposition assumes that the interaction space can be effectively captured by smaller subspaces, reducing the need for full n×n attention calculations.

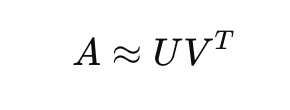
Here, U and V are low-rank matrices that significantly reduce complexity, enhancing the manageability of attention across long sequences. Thus, the attention computation becomes:

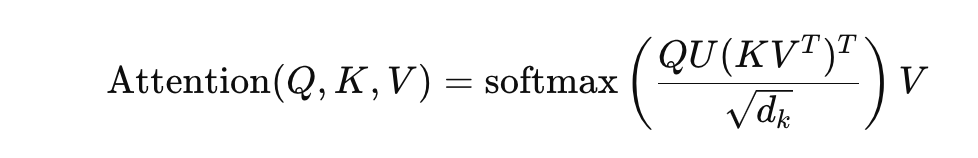
This method can significantly reduce computational load from O(n²) to O(nk).

Segmented Attention

Reduces computational complexity and memory requirements by partitioning the input sequence into smaller segments and computing attention independently over these segments.

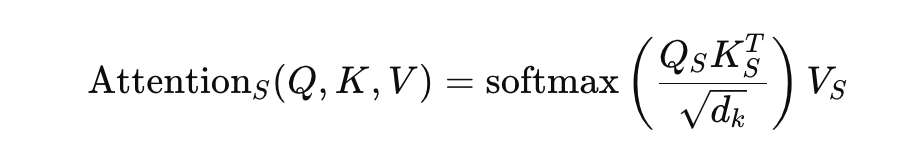Standard attention mechanisms are performed on each independent segment. This means that elements within each segment only interact with other elements within the same segment, rather than with elements across the entire sequence.

In some implementations, an additional step may be added after segmented attention to integrate information across different segments, ensuring that global context is not lost. This can be achieved through another layer of inter-segment attention or simple sequence-level operations (such as pooling or concatenation).

Hierarchical Attention

This attention model applies attention mechanisms hierarchically at different levels, allowing for more effective capture of structure and relationships in the data.

Data is organized into multiple levels, for example, in text processing, data can be structured into levels such as characters, words, sentences, and paragraphs. The model first computes attention at lower levels and then passes the results to higher levels. Each layer has its own representations for queries (Q), keys (K), and values (V), and attention weights are locally computed at each level and normalized through the softmax function. Higher-level attention mechanisms can synthesize outputs from lower levels to extract broader contextual information.

Here, G(⋅) represents a function that aggregates outputs across segments or layers, possibly incorporating additional transformations to refine attention processes across layers.

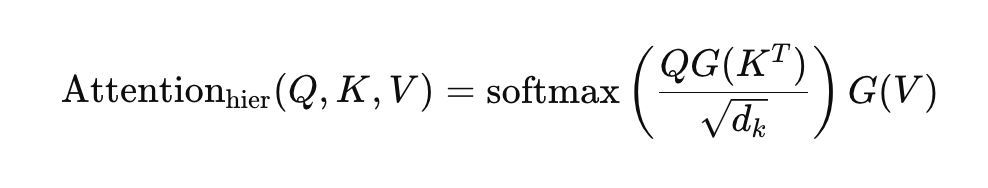
Recursive Memory

Incorporating memory into Transformers allows them to “remember” past computations, enhancing their ability to maintain context over longer sequences.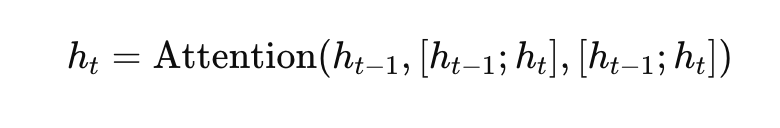

This recursive call integrates historical information, providing a continuous contextual clue that is essential for understanding sequences that extend beyond the current processing window.

Attention Mechanism with Routing

The attention mechanism with routing is an advanced neural network architecture often used in applications that require processing with complex internal structures or fine-tuning of information flow. This approach combines the flexibility of the attention mechanism with the decision-making process of dynamic routing protocols, achieving more efficient information processing.

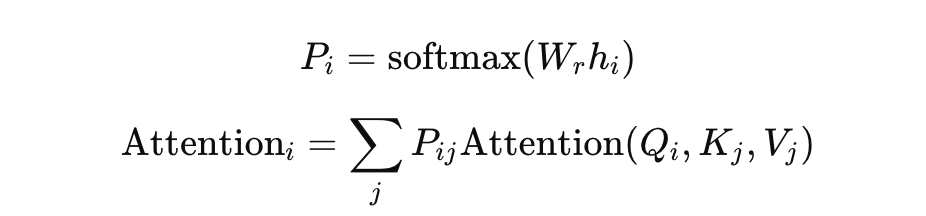
Here, W_r is a routing matrix that determines the probability distribution across different attention paths, allowing the model to dynamically adjust its focus based on the nature of the input.

In routing-based attention models, rather than simply applying the same attention weight computation method to all inputs, the flow of information is dynamically adjusted based on the characteristics and context of the input. This can be achieved through multiple attention heads, each responsible for processing different types of information. Routing decisions can be based on additional networks (such as dynamic routing algorithms in capsule networks), which use iterative processes to dynamically adjust the connection strengths between different components.

Relative Position Encoding

Relative position encoding uses the differences between positions to compute attention, rather than absolute position information.

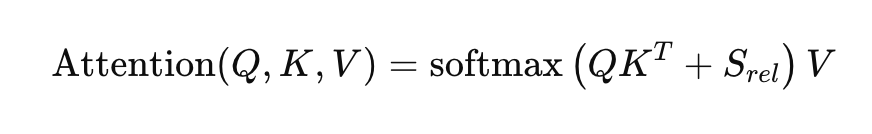S_rel represents the relative position bias, allowing the model to adjust its attention based on the relative distances and arrangements of tokens, enhancing its ability to handle different sequence lengths and structures.

Relative position encoding provides a more powerful and flexible way for Transformers and their variants to understand and process sequence data, which is particularly important for advanced tasks that require precise capture of complex relationships between elements.

Conclusion

This article comprehensively introduces several advanced attention mechanisms, by combining these methods, the Transformer architecture not only achieves computational efficiency but also enhances its ability to understand and generate context-rich and coherent outputs on extended sequences. These techniques not only improve the model’s capacity to handle complex data but also enhance its efficiency and generalization capabilities, showing broad application potential in various fields such as natural language processing and computer vision.

This article is sourced from STUDIO, copyright belongs to the original author, and is shared for informational purposes only. If there is any infringement, it will be removed immediately.

Editor / Garvey

Reviewer / Fan Ruiqiang

Verification / Garvey

Click below