[Introduction] Embedding representation learning is a current research hotspot. From Word2Vec to Node2Vec to Graph2Vec, a large number of X2Vec algorithms have emerged. But how can we construct a theory of vector embeddings to guide algorithm design? Recently, Professor Martin Grohe, a computer science professor at RWTH Aachen University and ACM Fellow, gave a report titled “X2Vec: Towards a Theory of Vector Embeddings for Structured Data,” which was very informative!

https://sigmod2020.org/pods_keynote.shtml

Martin Grohe is a computer scientist known for his research in parameterized complexity, mathematical logic, finite model theory, graph logic, database theory, and descriptive complexity theory. He is a professor of computer science at RWTH Aachen University, where he holds the chair of Discrete Systems Logic and Theory. In 1999, he received the Heinz Maier-Leibnitz Award from the German Research Foundation. He was elected as an ACM Fellow in 2017 for his contributions to logic in computer science, database theory, algorithms, and computational complexity.
Word2Vec, Node2Vec, Graph2Vec, X2Vec: Towards a Theory of Vector Embeddings of Structured Data
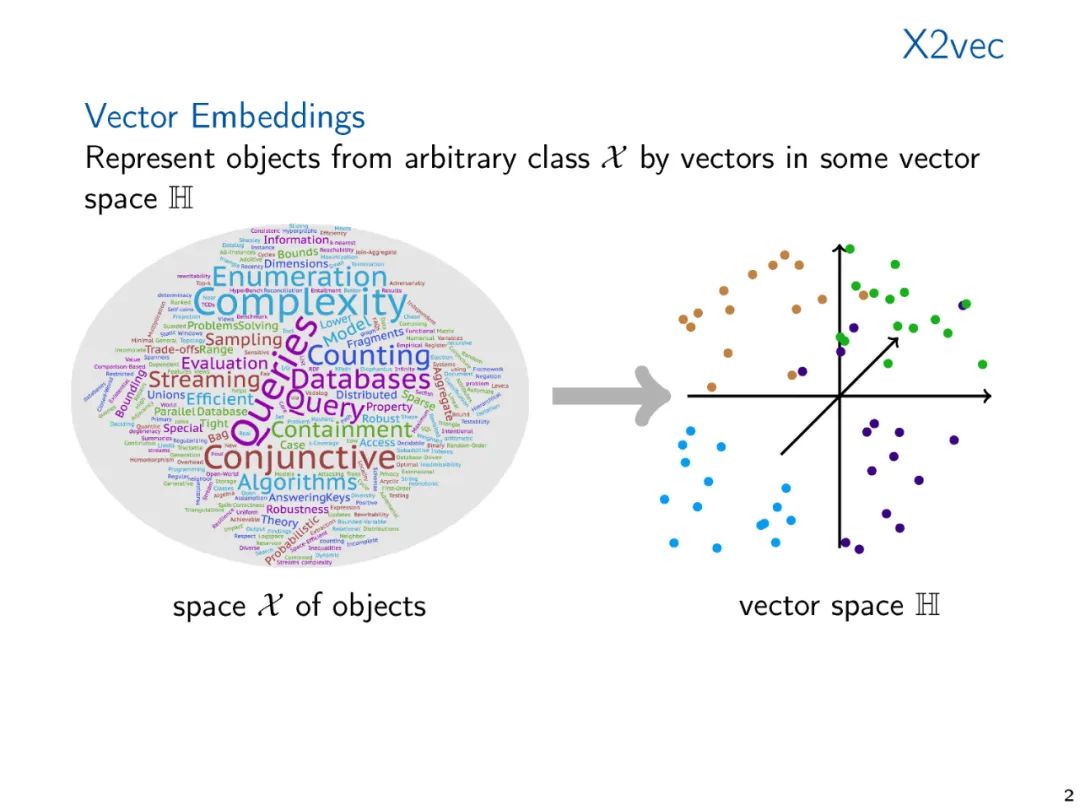
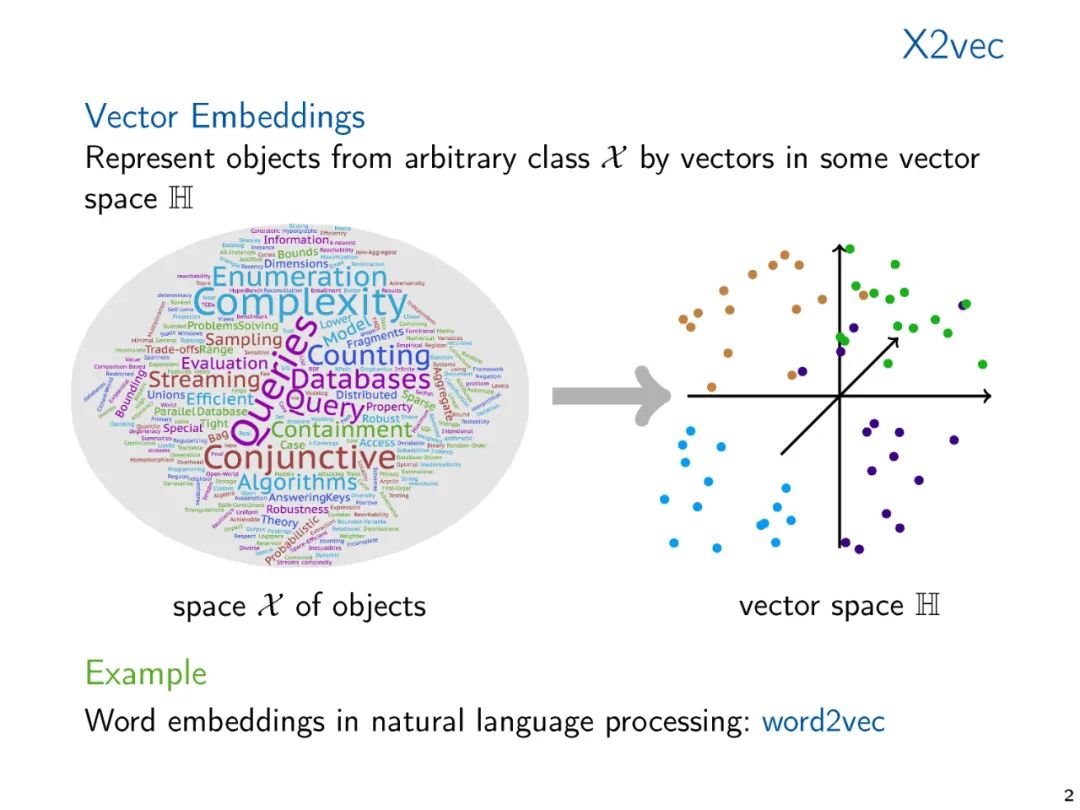
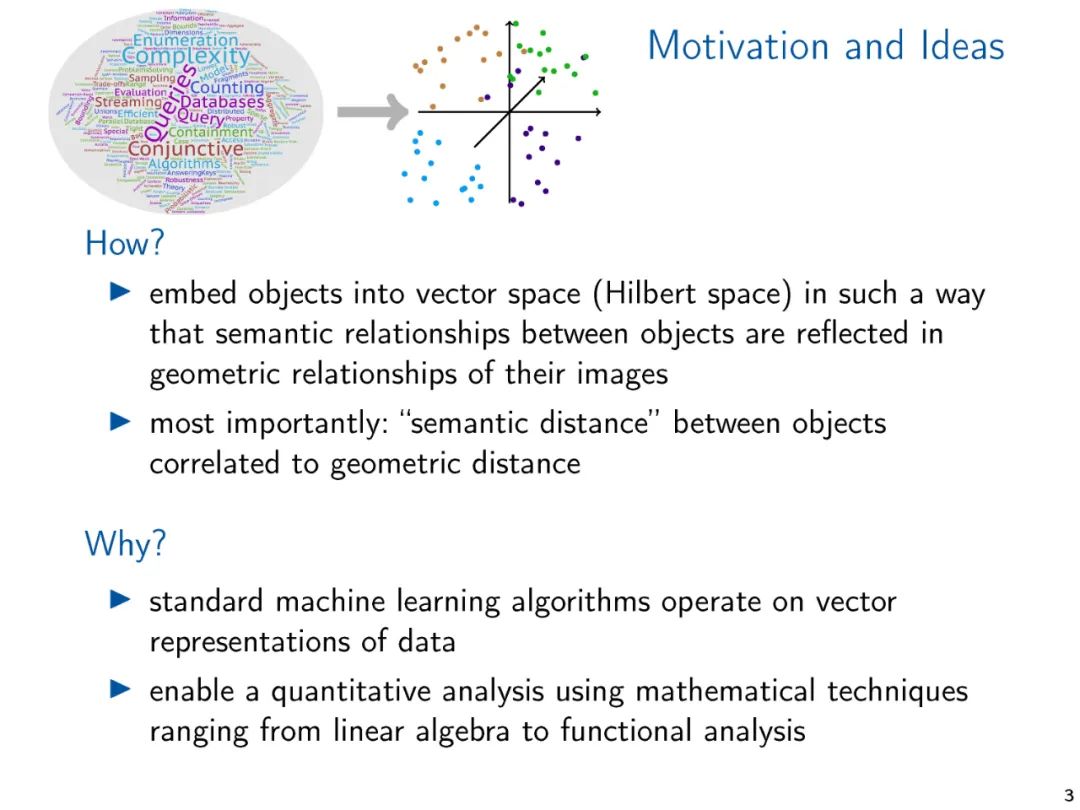
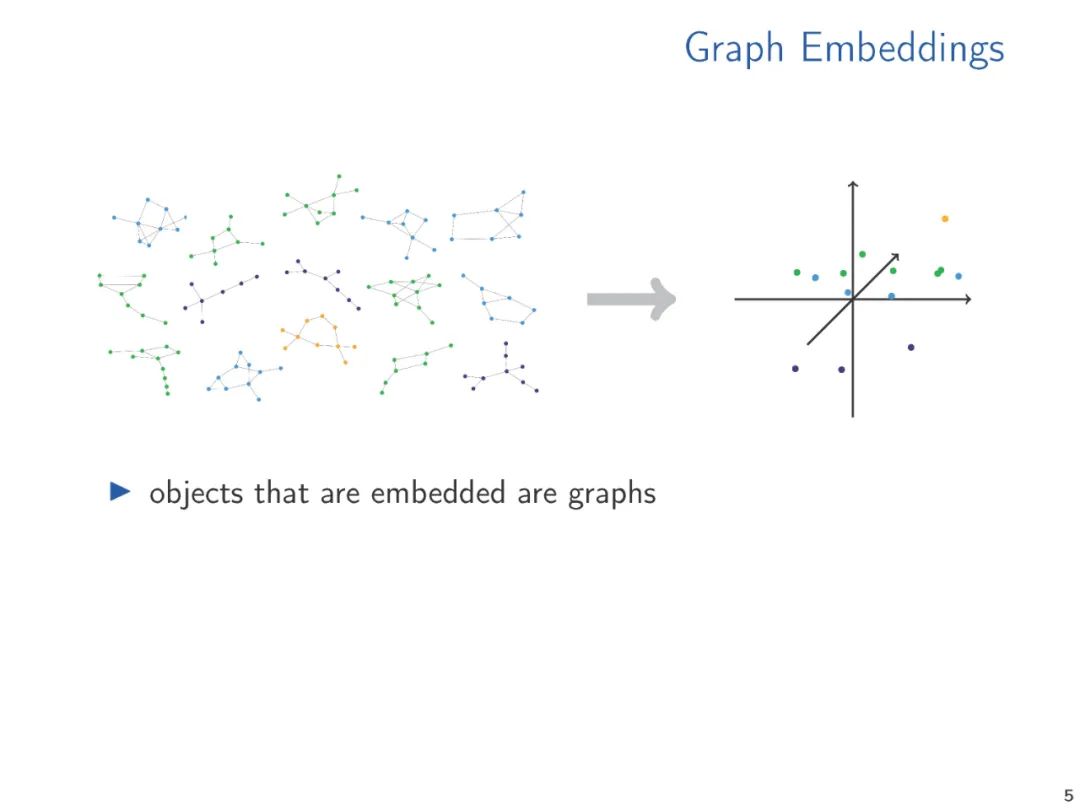
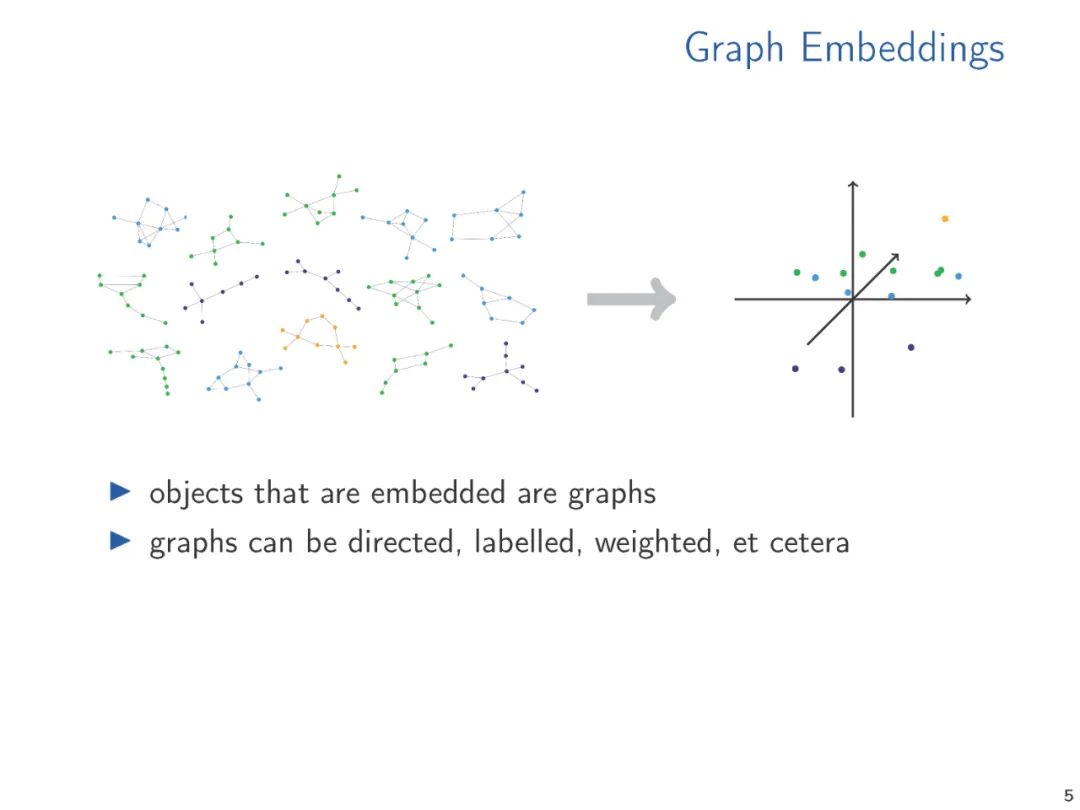
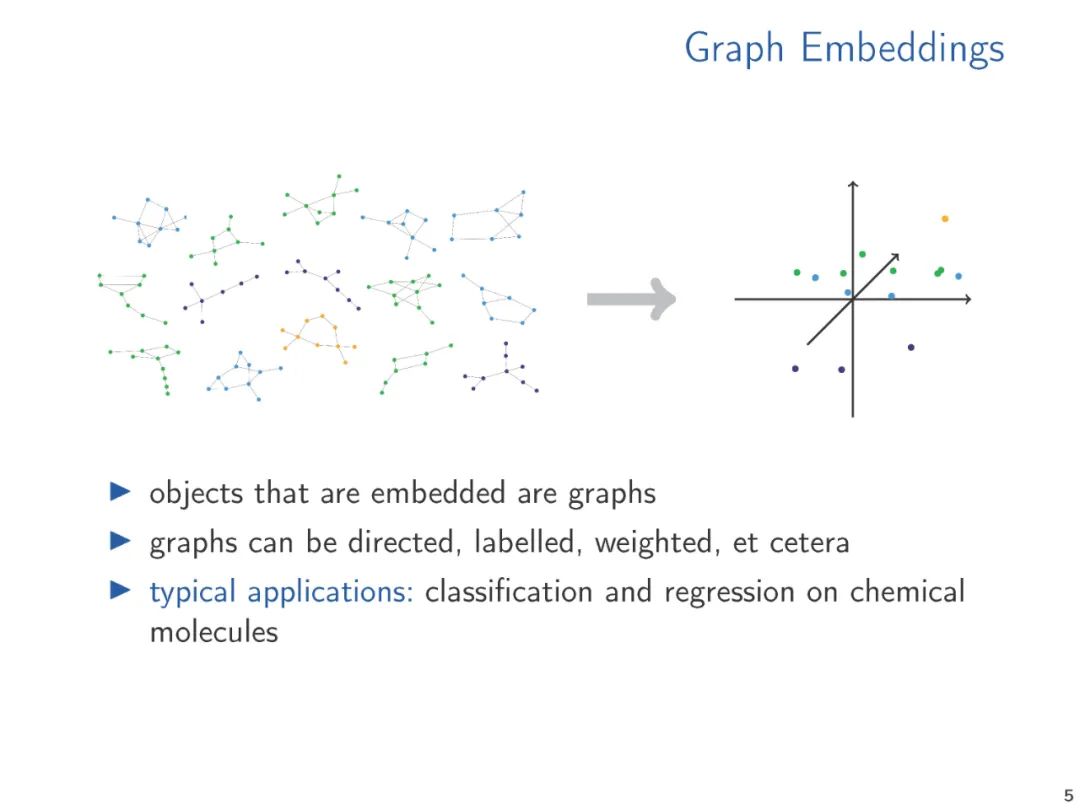
The vector representation of graphs and relational structures, whether hand-crafted feature vectors or learned representations, enables us to apply standard data analysis and machine learning techniques to structures. The methods for generating such embeddings have been widely studied in the machine learning and knowledge representation literature. However, from a theoretical perspective, vector embeddings have received relatively little attention. Starting with a survey of embedding techniques already in practical use, in this talk, we propose two theoretical approaches that we believe are central to understanding the foundations of vector embeddings. We connect various methods and propose directions for future research.
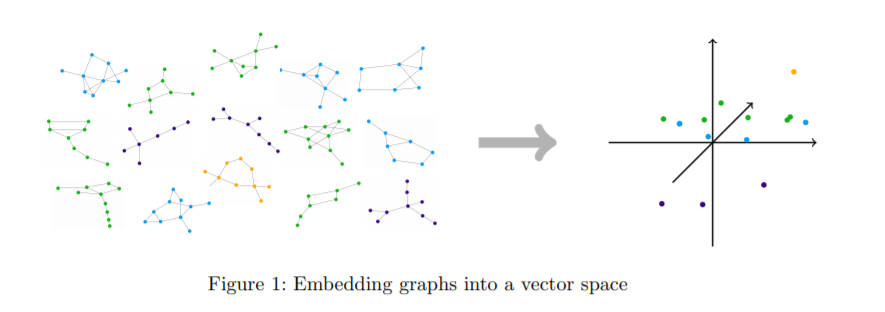
Typical machine learning algorithms require that symbolic data is represented as numerical vectors to perform computations on structured data. The vector representation of data ranges from manually designed features to learned representations, either computed through dedicated embedding algorithms or implicitly computed through learning architectures like graph neural networks. The performance of machine learning methods is critically dependent on the quality of the vector representations. Therefore, a large body of research has proposed a wide range of vector embedding methods for various applications. Most of this research is empirical, often targeting specific application domains. Given the importance of the topic, it is surprising that theoretical work on vector embeddings is relatively scarce, especially when it represents structural information that goes beyond metric information (i.e., distances in graphs).
The purpose of this paper is to outline various embedding techniques for structured data used in practice and to introduce theoretical ideas that can help understand and analyze these embedding techniques. The research prospects for vector embeddings are awkward, as different application domains (such as social network analysis, knowledge graphs, cheminformatics, computational biology, etc.) have driven several communities to largely study related issues independently. Therefore, we need to be selective and focus on the common ideas and connections we observe.
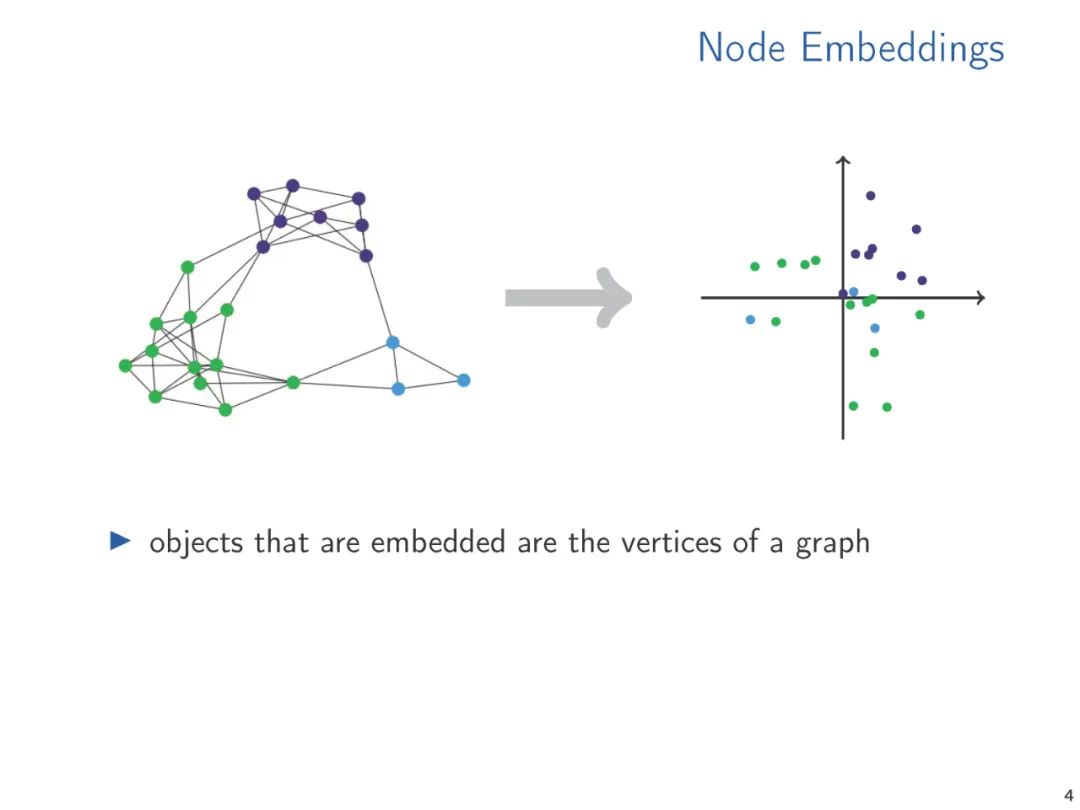
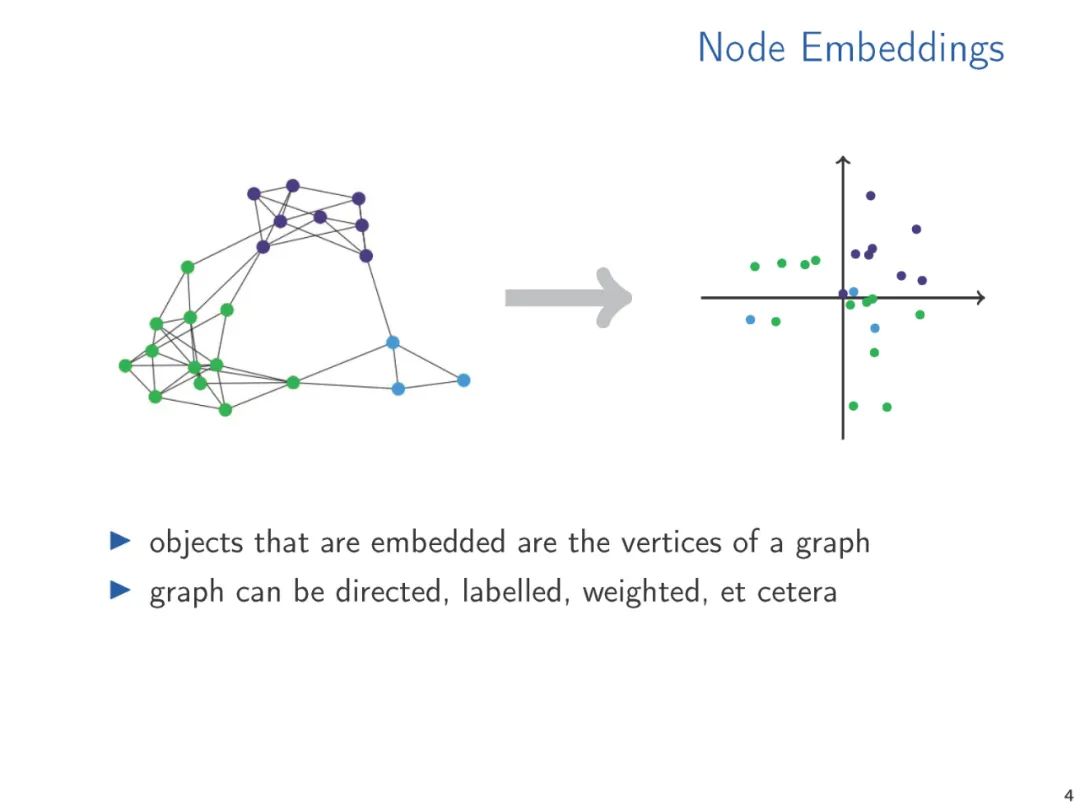
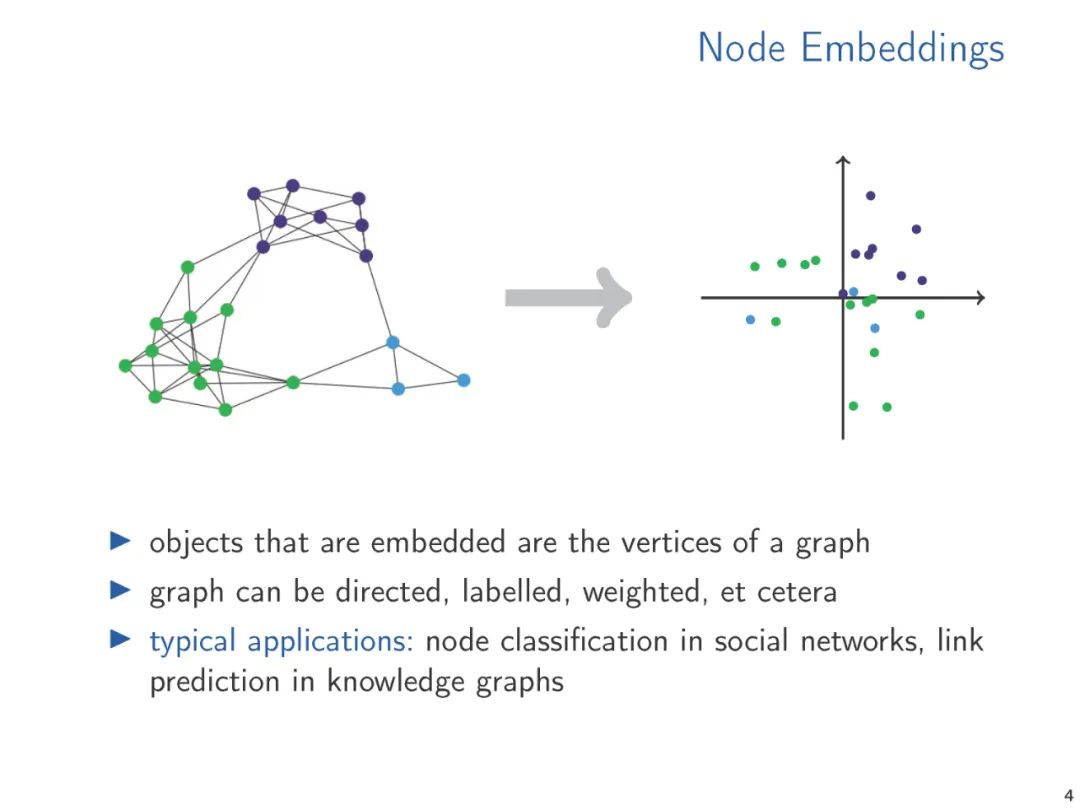
Vector embeddings can bridge the “discrete” world of relational data and the “differentiable” world of machine learning, thus having tremendous potential in database research. However, relatively little work has been done on embeddings of relational data beyond binary relations in knowledge graphs. Throughout the paper, I will attempt to point out potential directions for database-related research questions concerning vector embeddings.












Quick Access to Professional Knowledge
Convenient Download, please follow theProfessional Knowledge public account (click the blue above to follow)
Reply “x2vec” in the background to get the《Word2Vec, Node2Vec, Graph2Vec, X2Vec: Theory of Vector Embeddings, 120-page PPT》download link index