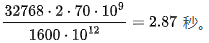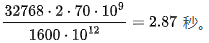Author | Aman Sanger
Compiled by OneFlow
Translation | Yang Ting, Wan Zi Lin
LLaMA-2-70B can be seen as a replacement for GPT-3.5, but if you are looking for cost-effectiveness, it is not wise to abandon OpenAI’s API.
Considering price and latency:
We should not use LLaMA-2 for strong generation-heavy workloads.
On the contrary, LLaMA is most suitable for prompt-heavy tasks like classification. The following situations are also suitable for choosing LLaMA-2:
In other tasks, GPT-3.5 is cheaper and faster than LLaMA 2.
Simply stated: one reason to use LLaMA instead of GPT-3.5 is fine-tuning (1). However, in this article, we only discuss cost and latency. I will not compare LLaMA-2 with GPT-4, as the former is closer to a 3.5-level model. Benchmark performance tests also support this view:
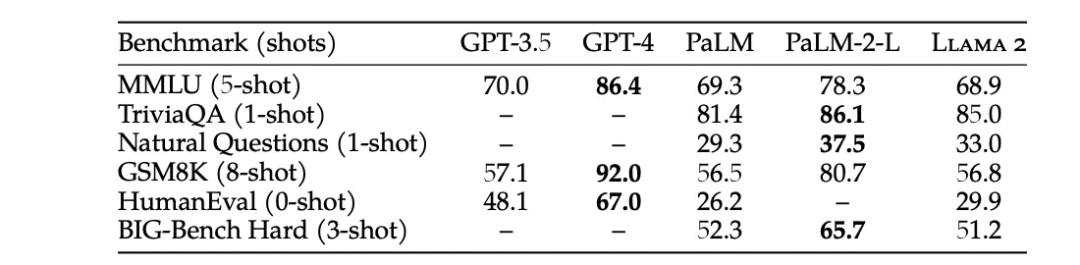
Figure 1: GPT-3.5 outperforms LLaMA in all benchmark tests (2)
With approximately the same latency, I will demonstrate the above assertion by comparing the costs of serving models using LLaMA-2-70B and GPT-3.5-turbo. We deployed LLaMA on 2 A100 GPUs with 80GB each, which is the minimum configuration required to load LLaMA into memory (16-bit precision) (3).
When testing with 2 A100s, we found that the pricing for LLaMA generating tokens is higher than that of GPT-3.5. We speculate that if tested with 8 A100 GPUs, LLaMA’s pricing would be more competitive, but at the cost of unacceptable high latency.
On the other hand, in terms of prompt tokens, LLaMA is over 3 times cheaper than GPT-3.5.
1 Basic Mathematical Principles of Transformers
Using some simple mathematical formulas, we derive the following formula for LLaMA-2. When the sequence length is N and the batch size is B :
Where 140 is twice the number of parameters of the model, and 320 KB/s is derived through arithmetic deduction. The following will explain how these numbers are derived.
There are also some papers and/or blog posts that provide excellent explanations of the mathematical principles of Transformers. For the inference part, Kipply’s article provides a good reference (4). Additionally, I believe the scaling law (5) generalizes the simplified formula used for Transformer FLOPs.
To verify these numbers, we start with the architectural details of LLaMA. The hidden dimension is 4096, the number of attention heads is 64, the number of layers is 80, and the dimension of each attention head is 128:
2 CalculationFloating Point Operations (FLOPs) of the Model
The FLOPs for forward propagation is approximately 2P, where P is the number of parameters in the model. Each parameter in the model belongs to a weight matrix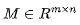 . For each input token, each matrix performs one operation with the vector representing that token.
For each M, we left-multiply with a vector x of dimension m. The total FLOPs for this vector-matrix multiplication is 2mn (6), which is twice the number of elements in the weight matrix. The total number of elements in all weight matrices of the Transformer is the total number of parameters of the model P, so ignoring the attention mechanism, there are a total of 2P FLOPs.
For relatively short sequences in large models like LLaMA, the contribution of attention to FLOPs can be neglected. The attention operations for each layer and each attention head are as follows:
. For each input token, each matrix performs one operation with the vector representing that token.
For each M, we left-multiply with a vector x of dimension m. The total FLOPs for this vector-matrix multiplication is 2mn (6), which is twice the number of elements in the weight matrix. The total number of elements in all weight matrices of the Transformer is the total number of parameters of the model P, so ignoring the attention mechanism, there are a total of 2P FLOPs.
For relatively short sequences in large models like LLaMA, the contribution of attention to FLOPs can be neglected. The attention operations for each layer and each attention head are as follows:
 It requires multiplying a
It requires multiplying a 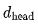 vector with a
vector with a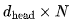 matrix to obtain
matrix to obtain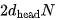 FLOPs. The scaling factor and Softmax can be neglected. Finally, multiplying the Attention vector with V requires additional
FLOPs. The scaling factor and Softmax can be neglected. Finally, multiplying the Attention vector with V requires additional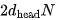 FLOPs. Summing the computations of all attention heads and layers gives
FLOPs. Summing the computations of all attention heads and layers gives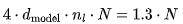 MFLOPs. Therefore, for the maximum sequence length of 8192, attention operations account for only 10.5 GFLOPs of the total 140 GFLOPs. This can be neglected for simplification.
3 Memory Requirements for Generation Tasks Are Higher Than for Prompt Tasks
When generating tokens, we need to re-read all model weights and the KV cache for each token generated. This means that to perform any matrix multiplication, we need to load the weights of each matrix from RAM into the GPU registers. When there are enough unique matrices, the actual loading of weights rather than the matrix multiplication itself becomes the bottleneck, so let’s compare the processing paths of prompt tokens and generated tokens in the model.
Memory Path for Generating Tokens through Transformers:
To illustrate this, we can roughly describe the path of a simple 1-layer Transformer generating a batch of tokens:
MFLOPs. Therefore, for the maximum sequence length of 8192, attention operations account for only 10.5 GFLOPs of the total 140 GFLOPs. This can be neglected for simplification.
3 Memory Requirements for Generation Tasks Are Higher Than for Prompt Tasks
When generating tokens, we need to re-read all model weights and the KV cache for each token generated. This means that to perform any matrix multiplication, we need to load the weights of each matrix from RAM into the GPU registers. When there are enough unique matrices, the actual loading of weights rather than the matrix multiplication itself becomes the bottleneck, so let’s compare the processing paths of prompt tokens and generated tokens in the model.
Memory Path for Generating Tokens through Transformers:
To illustrate this, we can roughly describe the path of a simple 1-layer Transformer generating a batch of tokens:
1. Read the input embedding matrix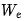 , and compute the corresponding embedding vectors for each input in the batch.
, and compute the corresponding embedding vectors for each input in the batch.
2. Read each matrix from memory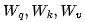 to compute the vectors for each input
to compute the vectors for each input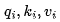 .
.
3. Attention operations – this requires reading the cached keys (key) and values (value). A vector is returned for each input.
4. Read from memory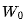 and multiply it with the output from the previous step.
and multiply it with the output from the previous step.
5. Read the output from step 1 and add it to the output from step 4, then perform layer normalization.
6. Read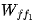 and perform multiplication to obtain the output of the first feedforward layer.
and perform multiplication to obtain the output of the first feedforward layer.
7. Read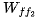 and perform multiplication to obtain the output of the second feedforward layer.
and perform multiplication to obtain the output of the second feedforward layer.
8. Read the output from step 5 and add it to the output from step 7, then perform layer normalization.
9. Read the non-embedding layer , then perform matrix multiplication to obtain the token probabilities for each input in the batch.
, then perform matrix multiplication to obtain the token probabilities for each input in the batch.
10. Sample the next token and feed it back to step 1.
Now let’s calculate the memory requirements. In steps 1, 2, 4, 6, 7, and 9, we roughly read all the parameters of the model once. (7) In step 3, we read the KV cache for each batch element. In all steps, we read intermediate activation values that can be neglected compared to the model size. Therefore, the memory bandwidth requirement is model weights + KV cache. Except for the KV cache, as the batch size increases, the memory requirement remains basically unchanged, which will be discussed in detail later. Note that this is the memory requirement for a single token.
Memory Path for Processing Prompt Tokens through Transformers:
When processing prompts, we read all model weights at once but incur the memory overhead of the attention mechanism. Consider the approximate path of a batch of sequences through the same Transformer:
-
Read the input embedding matrix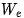 , and compute the corresponding embedding matrix for each sequence in the batch.
, and compute the corresponding embedding matrix for each sequence in the batch.
-
Read from memory 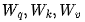 matrix to compute the matrix
matrix to compute the matrix 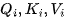 .
.
-
Perform attention operations.
-
Read from memory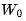 and multiply with the output from the previous step.
and multiply with the output from the previous step.
-
Read the output from step 1 and add it to the output from step 4, then perform layer normalization.
-
Read from memory 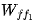 and perform multiplication to obtain the output of the first feedforward layer.
and perform multiplication to obtain the output of the first feedforward layer.
-
Read from memory 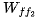 and perform multiplication to obtain the output of the second feedforward layer.
and perform multiplication to obtain the output of the second feedforward layer.
-
Read the output from step 5 and add it to the output from step 7, then perform layer normalization.
-
Read the non-embedding layer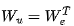 , then perform matrix multiplication to obtain the token probabilities for the prompt sequence.
, then perform matrix multiplication to obtain the token probabilities for the prompt sequence.
In steps 1, 2, 4, 6, 7, we read all the parameters of the model. In step 3, we perform attention operations, where the memory bandwidth needed for FlashAttention is significantly lower than that needed for reading model weights (applicable for reasonably long sequences and batch sizes). In all steps, we read activation values, which can be neglected compared to the model size (also applicable for reasonably long sequences and/or batches). Note that this is the memory requirement for all tokens.
In summary, the memory requirement for each token processed in prompt handling is significantly lower than that for generating tokens since we perform matrix multiplications in batches across the sequence dimension of the prompt tokens.
Memory Bandwidth Required for Model Weights:
Model weights at 16-bit precision occupy 140GB of memory.
Memory Bandwidth Required for KV Cache:
The size of the KV cache is the total size of all key-value pairs across all layers and attention heads in the neural network, with each token and batch element occupying 320MB for all previous tokens.
LLaMA 2 decides to remove multi-head attention. However, they use grouped query attention instead of multi-query attention to improve performance. This leads to 8 heads (or groups) for keys and values,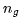 instead of the usual 128 heads for multi-head attention, and 1 head for multi-query attention.
For N tokens, the size of the KV cache is
instead of the usual 128 heads for multi-head attention, and 1 head for multi-query attention.
For N tokens, the size of the KV cache is 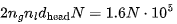 heads. Using 16-bit precision means 320N KB. Given a batch size of B, we get 320 ⋅NB KB.
For generation tasks, the memory requirement per token is:
For shorter sequences/small batches, the first term dominates. Otherwise, the second term becomes much larger. However, since we only have 160GB of memory and the model occupies 140GB, in our experiments, the KV cache will have some impact on memory bandwidth.
The memory bandwidth for prompt tokens is approximately:
Communication Computation Overhead:
For simplicity, we ignore the communication costs, as the parallel computation of the model significantly increases complexity. We can reasonably assume it will not slow down computation too much (especially since we split LLaMA across 2 GPUs).
4 The Cost of Prompt Processing Is Very Low
Prompt processing or the first token’s time is the most efficient part of Transformer inference, and it is expected to reduce the price by 3 times compared to GPT-3.5.
For a model with P parameters and a prompt of length N, the memory requirement for processing the prompt is approximately 2P bytes, and the computational requirement is 2PN FLOPs. Since the A100 can handle 312 TFLOPs of matrix multiplication and 2TB/s of memory bandwidth, when the sequence length N>156, computation becomes the limiting factor. (9)
On the A100, FLOPs utilization may approach 70% of the maximum floating-point computation execution rate (MFU), approximately 200 TFLOPs. The cost of two 80GB A100 GPUs is about $4.42 per hour (10), which is $0.0012 per second. The FLOPs required for each token of LLaMA is 140 TFLOPs. Considering the total FLOPs requirement of 2 A100 GPUs, the number of tokens per second can be derived as:
Compared to the price of GPT-3.5 at $0.0015 per 1000 tokens, this price is very affordable! It has nearly reduced by four times!
The latency is also very short! On our two GPUs, it should be able to process 512 tokens in 170 milliseconds and 1536 tokens in 530 milliseconds.
We can validate the above statements with actual data. We used the internal branch of HuggingFace’s text-generation-inference repository to measure the cost and latency of LLaMA-2.
heads. Using 16-bit precision means 320N KB. Given a batch size of B, we get 320 ⋅NB KB.
For generation tasks, the memory requirement per token is:
For shorter sequences/small batches, the first term dominates. Otherwise, the second term becomes much larger. However, since we only have 160GB of memory and the model occupies 140GB, in our experiments, the KV cache will have some impact on memory bandwidth.
The memory bandwidth for prompt tokens is approximately:
Communication Computation Overhead:
For simplicity, we ignore the communication costs, as the parallel computation of the model significantly increases complexity. We can reasonably assume it will not slow down computation too much (especially since we split LLaMA across 2 GPUs).
4 The Cost of Prompt Processing Is Very Low
Prompt processing or the first token’s time is the most efficient part of Transformer inference, and it is expected to reduce the price by 3 times compared to GPT-3.5.
For a model with P parameters and a prompt of length N, the memory requirement for processing the prompt is approximately 2P bytes, and the computational requirement is 2PN FLOPs. Since the A100 can handle 312 TFLOPs of matrix multiplication and 2TB/s of memory bandwidth, when the sequence length N>156, computation becomes the limiting factor. (9)
On the A100, FLOPs utilization may approach 70% of the maximum floating-point computation execution rate (MFU), approximately 200 TFLOPs. The cost of two 80GB A100 GPUs is about $4.42 per hour (10), which is $0.0012 per second. The FLOPs required for each token of LLaMA is 140 TFLOPs. Considering the total FLOPs requirement of 2 A100 GPUs, the number of tokens per second can be derived as:
Compared to the price of GPT-3.5 at $0.0015 per 1000 tokens, this price is very affordable! It has nearly reduced by four times!
The latency is also very short! On our two GPUs, it should be able to process 512 tokens in 170 milliseconds and 1536 tokens in 530 milliseconds.
We can validate the above statements with actual data. We used the internal branch of HuggingFace’s text-generation-inference repository to measure the cost and latency of LLaMA-2.
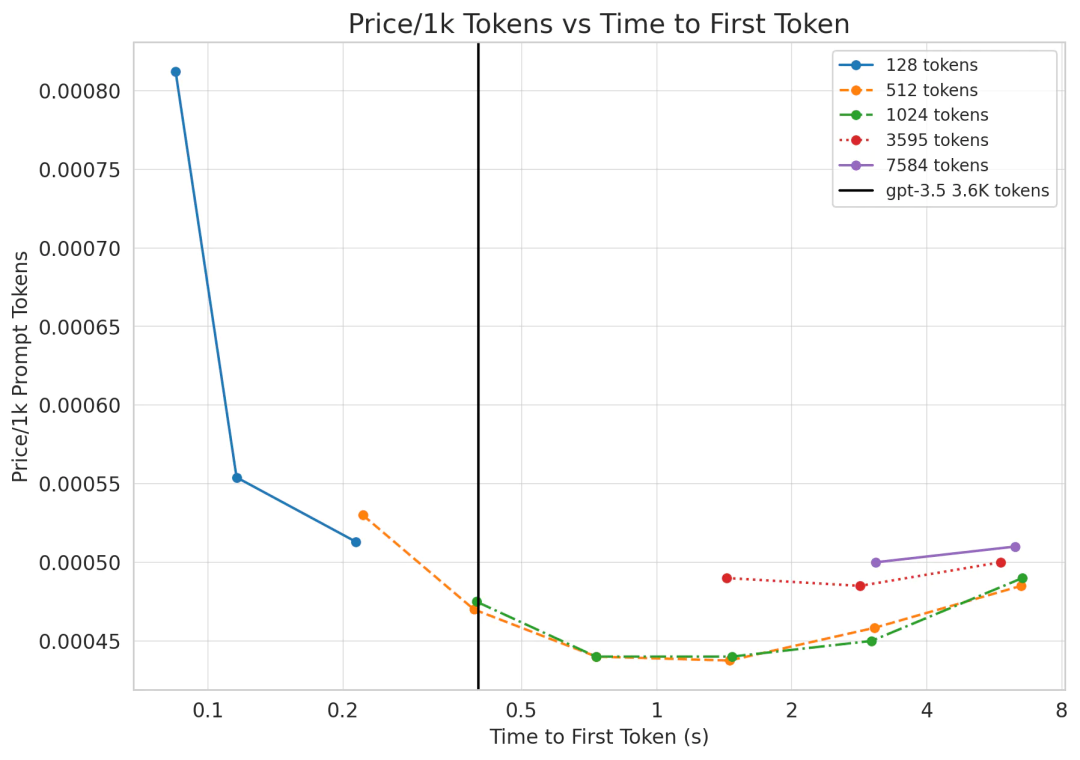
Figure 2: Each data point represents different batch sizes. For prompt tokens, LLaMA’s pricing is always much lower than GPT-3.5, but when generating 3.6K tokens, LLaMA’s latency slightly lags behind GPT-3.5’s 0.4 seconds.
As shown in the figure, compared to GPT-3.5’s price of $0.0015 per 1000 tokens, LLaMA’s price per 1000 tokens is much cheaper! For longer sequences, the latency of the first token seems slightly behind, but the solution is very simple. If LLaMA is parallelized across 8 GPUs (instead of 2 GPUs), the speed will increase nearly 4 times, meaning in prompt tasks, LLaMA-2 significantly outperforms GPT-3.5!
5 Token Generation Is Slow and Expensive
Theoretically, LLaMA-2’s token generation price in text generation is comparable to GPT-3.5, but in practice, the generation price of LLaMA-2 is higher and less competitive.
When generating tokens, we shift from a compute-bound state to a memory-bound state (11). Assuming a batch size of 1, we then determine the throughput we can achieve.
The peak memory bandwidth of each 80GB A100 GPU is 2TB/s per GPU. However, just like FLOPs utilization, in inference workloads (1.3 TB/s), you can only achieve about 60-70% utilization. Since the KV cache can be neglected in small batch processing, the throughput we can achieve on two A100 GPU chips is:
The new pricing is less competitive. Calculating at a price of $0.0012 per second, the cost is:
This pricing and speed are terrible for models at the level of GPT-3.5. But the previous notes about batch size indicate that due to such severe memory bottlenecks, we can increase the batch size without reducing generation speed. The larger the batch, the lower the cost.
However, we cannot increase the batch size indefinitely, as the KV cache will eventually occupy all GPU RAM. Fortunately, grouped query attention can alleviate this issue. In the case of N tokens and a batch size of B with 16-bit precision, the cache size is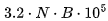 bytes. For example, with 4096 tokens and a batch size of 1, the cache size is 1.3GB. On two A100 GPUs, we have 160GB of space. Of this, the model occupies 135GB, leaving only 25GB available for the KV cache. Due to the additional inefficiency of memory storage, for longer sequence lengths, our maximum batch size is about 8.
With speed increasing (approximately) 8 times, we expect a price of $0.00825 per 1000 tokens. Although this price is still higher than that of gpt-3.5-turbo, it is getting closer. For shorter sequence lengths (totaling one thousand tokens), we can increase the batch size to 32, which means a price of $0.00206 per 1000 tokens. Theoretically, this price is competitive compared to gpt-3.5-turbo.
Another option is that we can also increase the number of GPUs. By renting 8 A100 GPUs with 80GB each, we get 1.28TB of memory. After removing the model weights, we still have over 1TB of memory available for the KV cache, which means a batch size of over 512 tokens can be achieved. It is worth noting that actual costs will not decrease by 512 times since the memory bandwidth occupied by the KV cache is 8 times larger than the model size, so costs may decrease by nearly 64 times.
Increasing computational resources can also solve latency issues. The throughput of GPT-3.5 is about 70 TPS. If the model is distributed over 8 GPUs instead of 2 GPUs, the throughput can increase to about 74.4 tokens per second.
While we did not use 8 A100 GPUs for this experiment, let’s look at the numerical situation on 2 80GB A100 GPUs.
6 Measured Generation Performance
bytes. For example, with 4096 tokens and a batch size of 1, the cache size is 1.3GB. On two A100 GPUs, we have 160GB of space. Of this, the model occupies 135GB, leaving only 25GB available for the KV cache. Due to the additional inefficiency of memory storage, for longer sequence lengths, our maximum batch size is about 8.
With speed increasing (approximately) 8 times, we expect a price of $0.00825 per 1000 tokens. Although this price is still higher than that of gpt-3.5-turbo, it is getting closer. For shorter sequence lengths (totaling one thousand tokens), we can increase the batch size to 32, which means a price of $0.00206 per 1000 tokens. Theoretically, this price is competitive compared to gpt-3.5-turbo.
Another option is that we can also increase the number of GPUs. By renting 8 A100 GPUs with 80GB each, we get 1.28TB of memory. After removing the model weights, we still have over 1TB of memory available for the KV cache, which means a batch size of over 512 tokens can be achieved. It is worth noting that actual costs will not decrease by 512 times since the memory bandwidth occupied by the KV cache is 8 times larger than the model size, so costs may decrease by nearly 64 times.
Increasing computational resources can also solve latency issues. The throughput of GPT-3.5 is about 70 TPS. If the model is distributed over 8 GPUs instead of 2 GPUs, the throughput can increase to about 74.4 tokens per second.
While we did not use 8 A100 GPUs for this experiment, let’s look at the numerical situation on 2 80GB A100 GPUs.
6 Measured Generation Performance
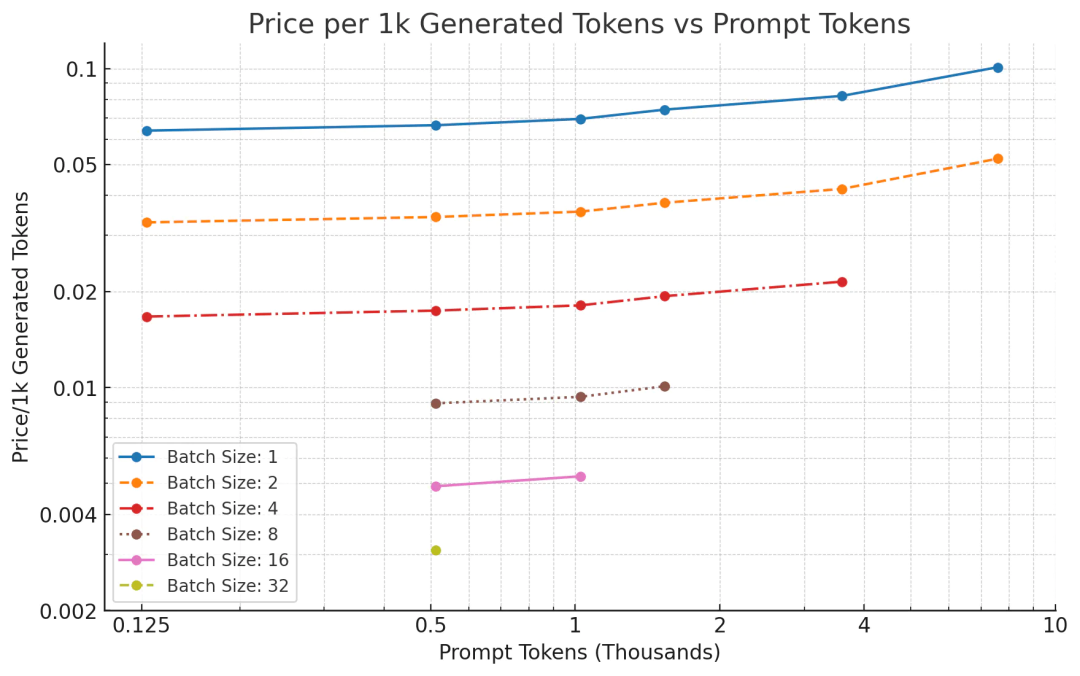
Figure 3: For all data points, we measured the cost of generating a single token when generating 512 tokens
These numbers are very close to the expected values calculated based on memory bandwidth.
However, as shown in the chart, although the generation cost per 1000 tokens decreases linearly with increasing batch size, there is still a gap compared to GPT-3.5’s pricing of $0.002 per 1000 tokens, especially for longer sequence lengths.
7 Large Batch Sizes Mean Unacceptable Latency
Using large batch sizes for generation can achieve pricing comparable to GPT-3.5, but will significantly increase the generation time of the first token. As the batch size increases, costs decrease linearly, but the generation time for the first token increases linearly.
When the batch size is 64, we can achieve a better price advantage than GPT-4, but will face the following situation:
For only 512 tokens, the generation time for the first token is close to 3 seconds! (12) When the batch size is 64 and the number of tokens is 3596, the generation time is 20.1 seconds. (13) Therefore, compared to OpenAI’s API, LLaMA-2 is more suitable for the following types of workloads:
1. Scenarios with a lot of prompts but few or zero generated tokens – very simple to handle pure prompt tasks.
2. Scenarios with few prompts or no prompts for token generation – we can adjust the batch size to above 64 to achieve competitive pricing compared to gpt-3.5-turbo without sacrificing latency.
3. Offline batch processing tasks that do not prioritize latency.
Increasing batch size requires a relatively large workload, which is not feasible for most startups! For most users and most workloads, the usage is extremely unstable. Of course, one solution is to automatically adjust the GPU scaling based on demand, but even so, on average each GPU is expected to only reach 50% of the maximum throughput – especially when considering cold start times.
Based on the above situation, we recommend using open-source models for prompt-based tasks and leaving generation tasks to closed-source models like GPT-3.5.
Most quantization methods incur losses, which means performance will decline. Through 8-bit quantization, we are likely to achieve performance with basic competitiveness, reducing all computed prices by 2 times! Although quantization and imperfect utilization will offset each other, considering this factor comprehensively, we expect the prices to be comparable to the measured prices.
However, most open-source quantization methods aim to make models easy to deploy on a small scale of consumer-grade GPUs rather than optimizing throughput at scale.
Several open-source libraries are specifically optimized for lower precision quantization while maintaining performance. However, these libraries are optimized for deploying models on a small scale of non-datacenter GPUs and are not designed for large-scale throughput needs. Specifically, they are mainly optimized for low-batch inference scenarios (mainly batch size of 1). While they can provide (in the best case) a 3-4 times speedup, the generation still costs $0.017 per 1000 tokens.
The Bits and Bytes library provides (effectively) lossless quantization, meaning it does not affect performance. However, its main advantage is reducing memory usage rather than improving speed. For example, the recent NF4 representation can only speed up matrix multiplication but not the inference throughput speed. Empirically, it seems that no speed improvements have been measured in this regard. (14)
It is still unclear how it will scale to larger batches.
The LLaMA.cpp library is mainly optimized for Apple hardware but also supports CUDA and fast 4-bit precision inference, but naive quantization here may significantly reduce performance.
Additionally, the LLaMA.cpp library is optimized for low-batch scenarios.
GPT-Q is another quantization library. Although I have not yet tested GPT-Q, I have been planning to do so. I hope we can use GPT-Q to reduce prices by 2 times!
Again, it is emphasized that this implementation is optimized for low-batch scenarios. Additionally, the speedup of more than 3 times mentioned in the paper only applies to 3-bit quantization, which has too great a loss for our use case.
10 How Are Closed-Source Model Prices Cheaper?
Closed-source models employ several methods to accelerate the inference process.
As mentioned earlier, we have several reliable open-source quantization methods, but I believe that OpenAI’s quantization implementation is more suitable for large-batch optimization.
It is widely speculated that GPT-4 uses the mixture of experts technique (15). If GPT-3.5-turbo also uses this technology, then to achieve the same performance level, you can deploy a smaller (and thus faster) model.
Adaptive sampling avoids the slow decoding of language models by allowing a smaller model to continuously generate multiple tokens (16). It is noteworthy that in the long run, this does not significantly improve throughput but can greatly reduce latency. As a reference, this codebase(https://github.com/dust-tt/llama-ssp.git) implements a simplified version of adaptive sampling.
Large-Scale Inference Techniques
During large-scale inference, OpenAI may use some techniques, such as allocating multiple 8-GPU nodes for pre-filling a batch of requests and then allocating a separate 8-GPU node for generating tokens for that request batch. This can take advantage of both advantages, allowing for batch sizes greater than 64 while achieving extremely low first token generation times.
We apply the above findings to guide companies on how and when to use open-source models. We find that open-source models are very suitable for prompt-based tasks such as classification or reordering.
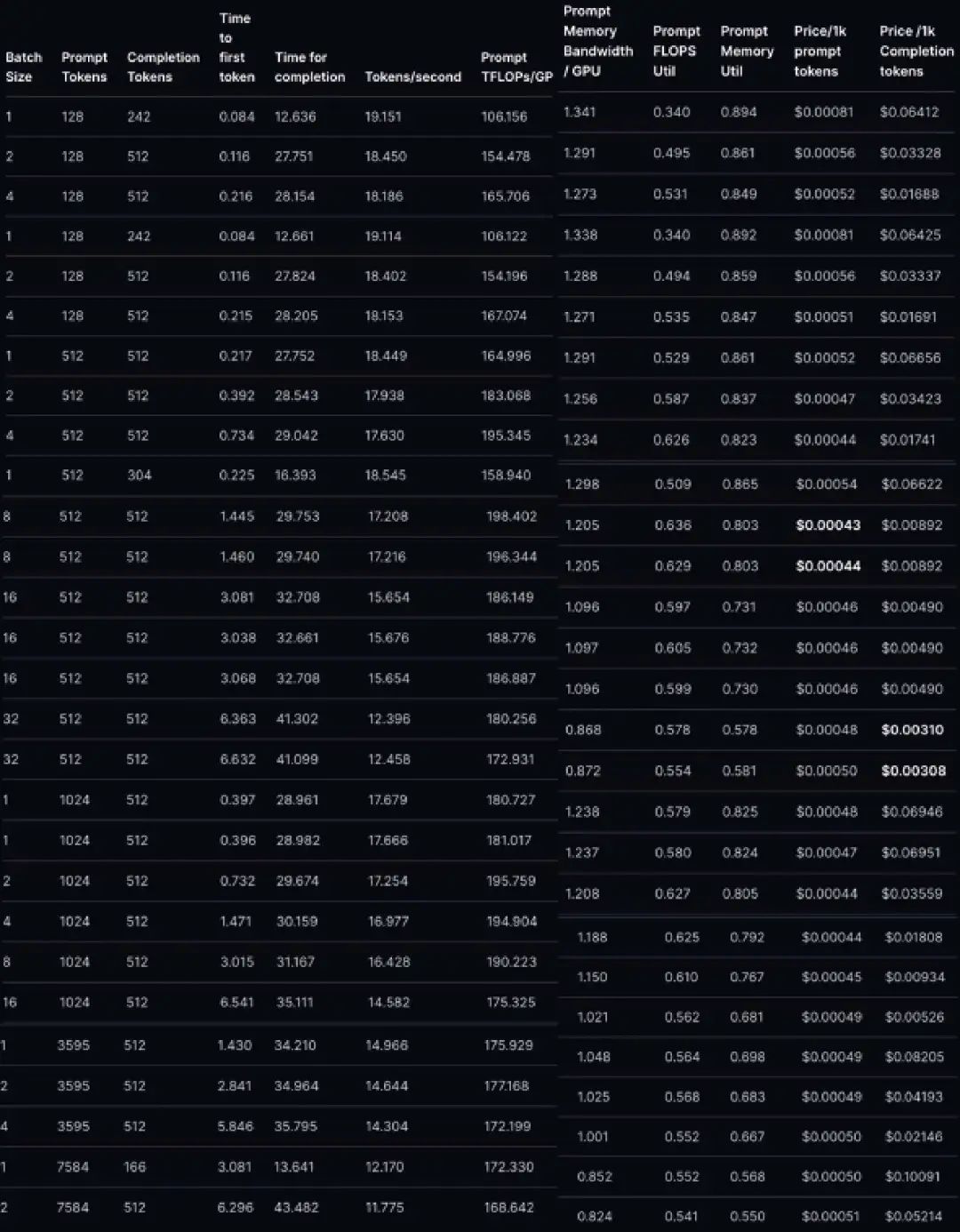
The following table shows the latency data points for LLaMA-2-70B, along with some additional computational metrics.
(1) Although we are funded by OpenAI, we have tried to maintain a fair and impartial attitude in the analysis of this article. For example, we believe that open-source models are more suitable for handling prompt-based tasks than gpt-3.5.
(2) https://ai.meta.com/research/publications/LLaMA-2-open-foundation-and-fine-tuned-chat-models/
(3) Despite the capacity, I could not configure any 4/8-GPU nodes.
(4) Chen, Carol. “Transformer Inference Arithmetic”,https://kipp.ly/blog/transformer-inference-arithmetic/, 2022.
(5) https://arxiv.org/abs/2001.08361
(6) In the multiplication of matrix 1xm and matrix mxn, the calculation of FLOPs can be proved by simple deduction. The dot product between two k-dimensional vectors requires 2k FLOPs because we perform k independent multiplication operations and then k addition operations to sum the array of products. Matrix multiplication executes l·n dot product operations, where each vector is m-dimensional. This means the total FLOPs for matrix multiplication is 2mnl. In vector-matrix multiplication, l=1, so the FLOPs are only 2mn.
(7) We read the embedding matrix twice, but compared to the model size, it is very small and can even be neglected.
(8) At sufficiently large sequence lengths, the actual stored intermediate activations will use more memory bandwidth than the model weights, comparable to the usage of flash-attention. This paper used techniques similar to flash-attention to reduce the memory bandwidth consumption of these intermediate activations: https://arxiv.org/pdf/2305.19370.pdf
(9) In fact, this may be the reason why the generation time for the first token on short prompts is almost constant. Computation/token and memory bandwidth per token can be represented as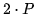 or 2 times. Since A100’s FLOPs at 16-bit precision are 312, memory bandwidth only depends on the number of tokens generated, while FLOPs depend on the number of prompt and generated tokens, thus until the number of prompt tokens reaches
or 2 times. Since A100’s FLOPs at 16-bit precision are 312, memory bandwidth only depends on the number of tokens generated, while FLOPs depend on the number of prompt and generated tokens, thus until the number of prompt tokens reaches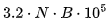 tokens, the time for the first token is limited by memory bandwidth (thus remains constant).
(10) https://www.coreweave.com/gpu-cloud-pricing
(11) Considering LLaMA’s memory and computational requirements, convince yourself this is true.
(12) On 8-A100s, we can expect to perform
tokens, the time for the first token is limited by memory bandwidth (thus remains constant).
(10) https://www.coreweave.com/gpu-cloud-pricing
(11) Considering LLaMA’s memory and computational requirements, convince yourself this is true.
(12) On 8-A100s, we can expect to perform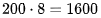 TFLOPs of computation. However, for the case of 64 batch size, 512 prompt tokens, totaling 32768 tokens, this means the delay for computation will be
TFLOPs of computation. However, for the case of 64 batch size, 512 prompt tokens, totaling 32768 tokens, this means the delay for computation will be
(13) In the same case where we can perform 1600 TFLOPs of computation, we need to process 3596 prompt tokens. First, in this sequence length and batch size, we are likely to again be limited by memory bandwidth, further slowing processing speed. Even without considering memory bandwidth limitations, processing time will slow down by 7 times compared to before, meaning it will take 20.09 seconds.
(14) See the blog post from huggingface and this tweet.
(15) https://www.semianalysis.com/p/gpt-4-architecture-infrastructure
(16) https://arxiv.org/pdf/2302.01318.pdf




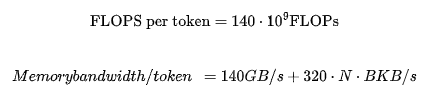
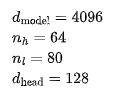
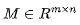 . For each input token, each matrix performs one operation with the vector representing that token.
. For each input token, each matrix performs one operation with the vector representing that token.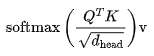
 It requires multiplying a
It requires multiplying a 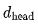 vector with a
vector with a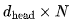 matrix to obtain
matrix to obtain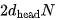 FLOPs. The scaling factor and Softmax can be neglected. Finally, multiplying the Attention vector with V requires additional
FLOPs. The scaling factor and Softmax can be neglected. Finally, multiplying the Attention vector with V requires additional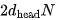
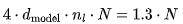 MFLOPs. Therefore, for the maximum sequence length of 8192, attention operations account for only 10.5 GFLOPs of the total 140 GFLOPs. This can be neglected for simplification.
MFLOPs. Therefore, for the maximum sequence length of 8192, attention operations account for only 10.5 GFLOPs of the total 140 GFLOPs. This can be neglected for simplification.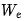 , and compute the corresponding embedding vectors for each input in the batch.
, and compute the corresponding embedding vectors for each input in the batch.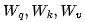 to compute the vectors for each input
to compute the vectors for each input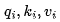 .
.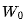 and multiply it with the output from the previous step.
and multiply it with the output from the previous step.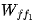 and perform multiplication to obtain the output of the first feedforward layer.
and perform multiplication to obtain the output of the first feedforward layer.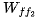 and perform multiplication to obtain the output of the second feedforward layer.
and perform multiplication to obtain the output of the second feedforward layer. , then perform matrix multiplication to obtain the token probabilities for each input in the batch.
, then perform matrix multiplication to obtain the token probabilities for each input in the batch.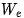 , and compute the corresponding embedding matrix for each sequence in the batch.
, and compute the corresponding embedding matrix for each sequence in the batch.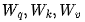 matrix to compute the matrix
matrix to compute the matrix 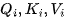
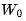
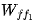 and perform multiplication to obtain the output of the first feedforward layer.
and perform multiplication to obtain the output of the first feedforward layer.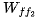 and perform multiplication to obtain the output of the second feedforward layer.
and perform multiplication to obtain the output of the second feedforward layer.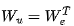
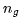 instead of the usual 128 heads for multi-head attention, and 1 head for multi-query attention.
instead of the usual 128 heads for multi-head attention, and 1 head for multi-query attention.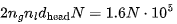 heads. Using 16-bit precision means 320N
heads. Using 16-bit precision means 320N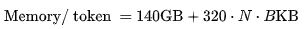
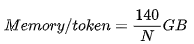
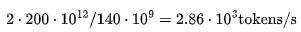
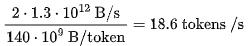
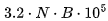 bytes. For example, with 4096 tokens and a batch size of 1, the cache size is 1.3GB. On two A100 GPUs, we have 160GB of space. Of this, the model occupies 135GB, leaving only 25GB available for the KV cache. Due to the additional inefficiency of memory storage, for longer sequence lengths, our maximum batch size is about 8.
bytes. For example, with 4096 tokens and a batch size of 1, the cache size is 1.3GB. On two A100 GPUs, we have 160GB of space. Of this, the model occupies 135GB, leaving only 25GB available for the KV cache. Due to the additional inefficiency of memory storage, for longer sequence lengths, our maximum batch size is about 8.

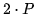 or 2 times. Since A100’s FLOPs at 16-bit precision are 312, memory bandwidth only depends on the number of tokens generated, while FLOPs depend on the number of prompt and generated tokens, thus until the number of prompt tokens reaches
or 2 times. Since A100’s FLOPs at 16-bit precision are 312, memory bandwidth only depends on the number of tokens generated, while FLOPs depend on the number of prompt and generated tokens, thus until the number of prompt tokens reaches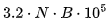 tokens, the time for the first token is limited by memory bandwidth (thus remains constant).
tokens, the time for the first token is limited by memory bandwidth (thus remains constant).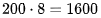 TFLOPs of computation. However, for the case of 64 batch size, 512 prompt tokens, totaling 32768 tokens, this means the delay for computation will be
TFLOPs of computation. However, for the case of 64 batch size, 512 prompt tokens, totaling 32768 tokens, this means the delay for computation will be