
Source: Machine Heart
This article is about 4500 words long and is recommended to be read in 5 minutes.
What can a 13-layer Transformer do? It can simulate a basic calculator, a basic linear algebra library, and execute an in-context learning algorithm using backpropagation.
Transformers have become a popular choice for various machine learning tasks, achieving great results. So how else can they be used? Researchers with open minds have even thought about using them to design programmable computers!
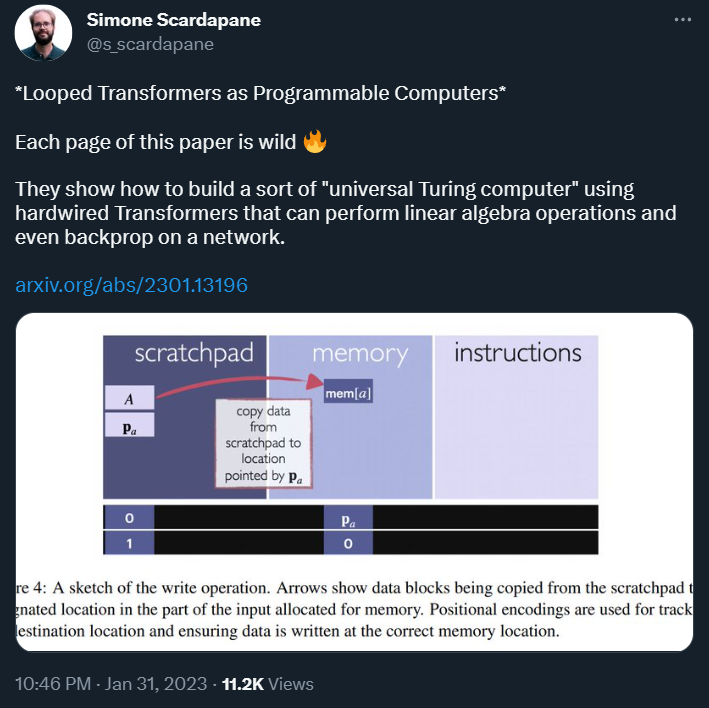
The authors of this paper are from Princeton University and the University of Wisconsin, titled “Looped Transformers as Programmable Computers,” aiming to explore how to implement a universal computer using Transformers.
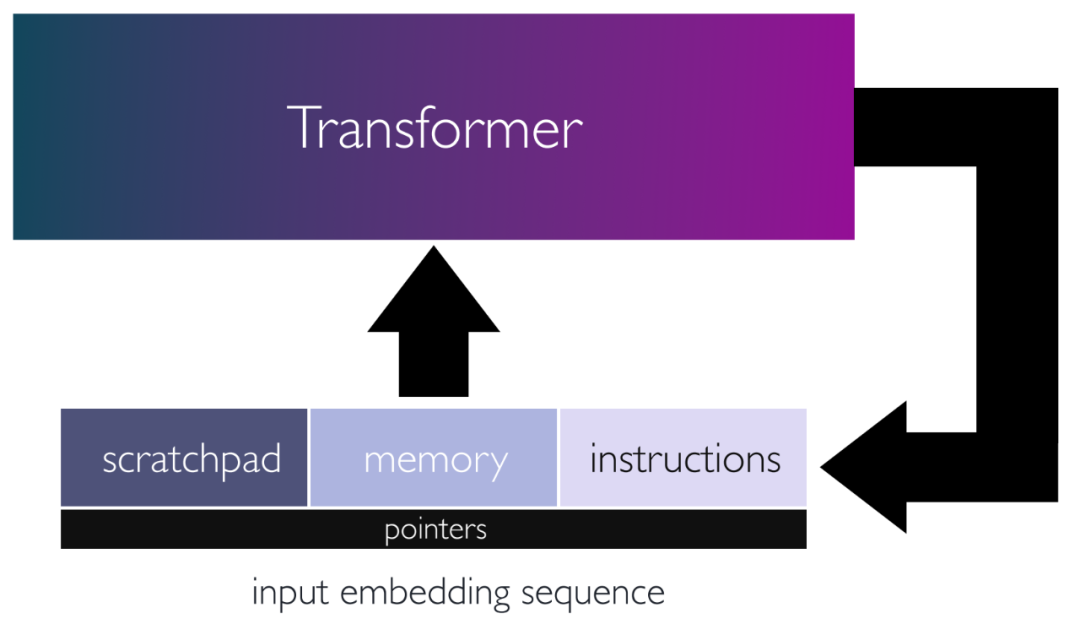
Specifically, the authors propose a framework that uses transformer networks as universal computers by programming them with specific weights and placing them in a loop. In this framework, the input sequence acts as punched cards, consisting of instructions and memory for data read/write.
The authors demonstrate that a constant number of encoder layers can simulate basic computational blocks. Using these building blocks, they simulate a small instruction set computer. This allows them to map iterative algorithms to programs that can be executed by a looped 13-layer transformer. They show how this transformer can simulate a basic calculator, a basic linear algebra library, and an in-context learning algorithm using backpropagation, under the guidance of its input. This work highlights the versatility of the attention mechanism and demonstrates that even shallow transformers can execute mature universal programs.
Paper Overview
Transformers (TF) have become a popular choice for various machine learning tasks, achieving state-of-the-art results in many problems in fields such as natural language processing and computer vision. One key reason for the success of Transformers is their ability to capture higher-order relationships and long-range dependencies through the attention mechanism. This enables TF to model contextual information, making it more effective in tasks like machine translation and language modeling, where Transformer performance has consistently outperformed other methods.
Language models with hundreds of billions of parameters, such as GPT-3 (175B parameters) and PaLM (540B parameters), have achieved state-of-the-art performance on many natural language processing tasks. Interestingly, some of these large language models (LLMs) can also perform in-context learning (ICL), adapting and executing specific tasks based on brief prompts and examples in real-time. The ICL capability of LLMs exists without needing retraining, allowing these large models to effectively perform new tasks without updating weights.
Surprisingly, through ICL, LLMs can perform algorithmic tasks and reasoning, and works by [Nye et al. [2021], Wei et al. [2022c], Lewkowycz et al. [2022], Wei et al. [2022b], Zhou et al. [2022]] have demonstrated its feasibility. Work by [Zhou et al. [2022]] has shown that when given a prompt with a multi-digit addition algorithm and some addition examples, LLMs can successfully perform addition on unknown cases. These results indicate that LLMs can execute pre-instructed commands based on algorithm principles during reasoning, as if interpreting natural language as code.
There is evidence that Transformers can simulate Turing machines or recursive links between attention layers with sufficient depth [Pérez et al. [2021], Pérez et al. [2019], Wei et al. [2022a]]. This demonstrates the potential of Transformer networks to precisely follow algorithmic instructions specified by the input. However, these constructs are relatively vague and do not provide deep insights into how to create Transformers capable of executing specific algorithmic tasks.
However, more specialized designs can enable TF to execute more advanced programs. For example, [Weiss et al. [2021]] designed a computational model and a programming language that maps simple selection and aggregation commands to indexed input tokens. This language can be used to create various interesting algorithms, such as token counting, sorting, creating histograms, and recognizing Dyck-k languages. Programs written in a restricted access sequence processing language (RASP) can then be mapped to Transformer networks, which typically vary in size with the size of the program.
Another study demonstrated a method for selecting Transformer model weights to serve as an optimization algorithm for dynamically learning linear regression models, performing implicit training during inference when given training data as input. These methods typically require a number of layers proportional to the number of iterations of the learning algorithm and are limited to a single loss function and model set.
Programming Transformer models to simulate abstract computations of Turing machines, specialized commands of languages like RASP, and specific algorithms of ICL highlights the potential of Transformer networks as versatile programmable computers.
The research by the authors of this paper aims to explore this promising prospect, revealing how the attention mechanism can simulate universal computers inspired by instruction set architectures.
Using Transformers as Programmable Computers
In this paper, the authors demonstrate that Transformer networks can simulate complex algorithms and programs by hard-coding them with specific weights and placing them in a loop. They achieve this by reverse engineering the attention to simulate basic computational blocks, such as editing operations on input sequences, nonlinear functions, function calls, program counters, and conditional branches. The authors’ paper proves the importance of connecting the output sequence of the Transformer back to its input using a single loop or recursion, avoiding the need for deep models.

Paper link:https://arxiv.org/pdf/2301.13196.pdf
The authors achieve this by designing a Transformer that can execute programs written in a universal version of a single instruction, called SUBLEQ (A,B,C), which means subtract and branch if less than or equal to zero. SUBLEQ is a single instruction language that defines a one-instruction set computer (OISC). SUBLEQ consists of three memory address operations; when executed, it subtracts the value at memory address A from the value at memory address B, storing the result back in B. If the result in B is less than or equal to 0, it jumps to address C; otherwise, it continues to execute the next instruction. However, this instruction can define a universal computer.
The authors constructed an explicit Transformer to implement a program similar to SUBLEQ, referred to as FLEQ, which is a more flexible single instruction with the form
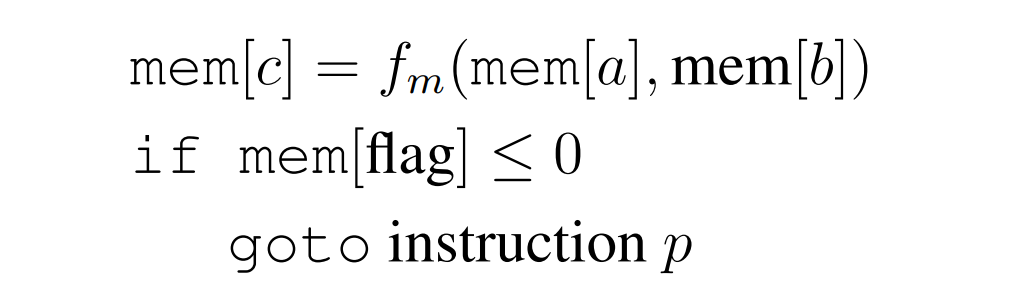
where f_m can be selected from a set of functions (matrix multiplication/nonlinear functions/polynomials, etc.) and can be hard-coded into the network. The depth of the looped Transformer that can execute FLEQ programs does not depend on the depth of the program or the number of lines of code, but rather on the depth required to implement a single FLEQ instruction, which remains constant. This is achieved by running the Transformer in a loop over the input sequence, similar to how a CPU operates.
Using this framework, the authors demonstrate the ability to simulate various functions during inference, including a basic calculator, a basic linear algebra library (matrix transposition, multiplication, inversion, power iteration), and implementing backpropagation in implicit fully connected networks for ICL. The input sequence or prompt can be treated as punched cards, including the instructions the Transformer needs to execute while providing space for storing and processing variables used in the program. The depth of the Transformer networks used to execute these programs is less than or equal to 13, and all weight matrices of these models are provided. The theorem below summarizes the authors’ main findings:
Theorem 1: There exists a looped Transformer with fewer than 13 layers that can simulate a universal computer (as described in Section 5 of the paper), a basic calculator (as described in Section 7), numerical linear algebra methods such as approximate matrix inversion and power iteration (as described in Section 8), and neural network-based ICL algorithms (such as SGD) (as described in Section 9).
The authors’ research emphasizes the flexibility of the attention mechanism and the importance of a single loop, enabling the design of models capable of simulating complex iterative algorithms and executing universal programs. It further demonstrates the ability of Transformer models to efficiently perform complex mathematical and algorithmic tasks. It can be imagined that modern Transformers (like GPT-3), when executing various tasks, use similar internal subroutines. To some extent, when given contextual examples and instructions, these models can be inspired to perform specific techniques or algorithms, similar to function calls. However, this hypothesis should be approached with caution, as the way the authors designed the structure has no resemblance to how real-world language models are trained.
The authors hope their research will encourage further exploration of the potential of the attention mechanism and the ability of language models to execute algorithmic instructions. The design proposed by the authors can help determine the minimum size of Transformer networks required to perform specific algorithmic tasks. Additionally, the authors hope their findings will contribute to inspiring the development of methods that leverage smaller, reverse-engineered Transformer networks to accomplish specific algorithmic tasks, thereby enhancing the training capabilities of language models.
Building Transformer Modules for Universal Computation
To construct a universal computational framework using Transformer networks, specialized computational blocks are needed. These blocks are assembled to create the desired final functionality. Below, various operations that Transformer layers can perform are highlighted. These operations will provide the foundation for creating more complex routines and algorithms. The purpose of these operations is to be interoperable with each other, leveraging attention to perform various tasks such as generating approximate permutation matrices and approximating general functions through sigmoid functions.
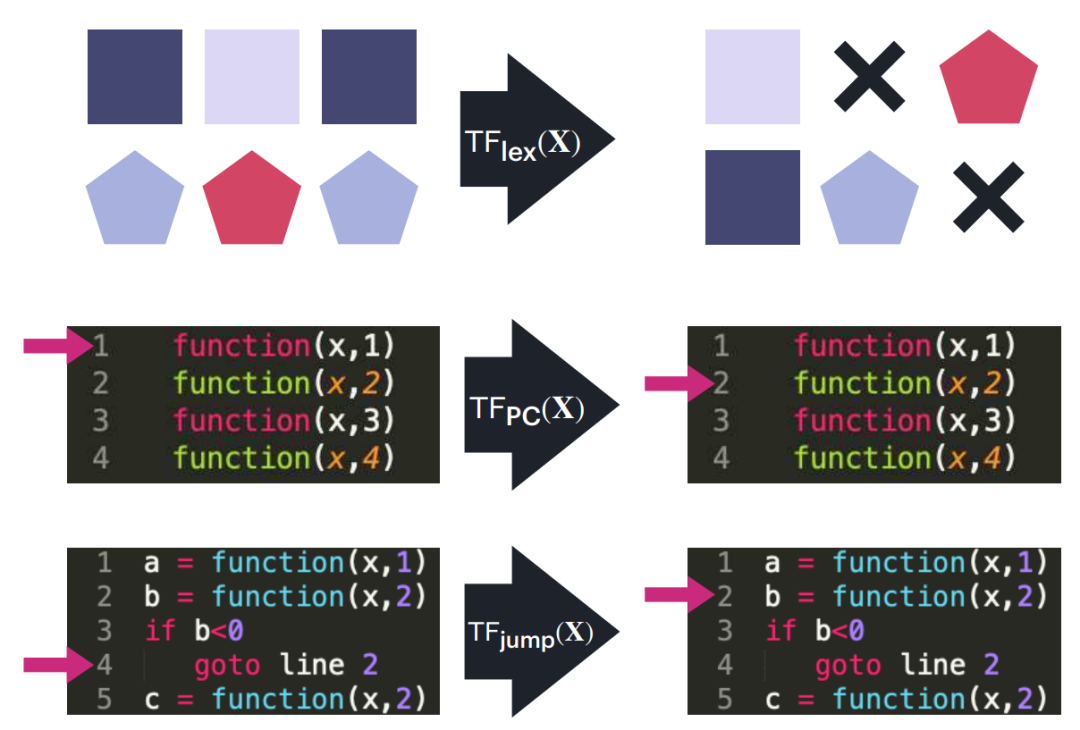
Positional Encoding, Program Counter, and Data Pointer
Transformers typically need to perform iterative algorithms or execute a series of commands. To achieve this, the authors use a loop to access the commands via a program counter. The counter contains encodings that store the position of the next command. Additionally, commands may have data pointers pointing to the data locations that need to be read and written. Both the program counter and data pointer use the same positional encoding discussed in the previous section.

The authors’ positional encoding scheme can also be used to point to specific data locations for reading or writing, which will be discussed in the next section. This is achieved by using the same binary vector for the positional encodings of both the program counter and data pointer. Furthermore, this technique for pointing to specific data locations allows the Transformer to efficiently read/write data during the execution of algorithms or command sequences being constructed.
Read/Write: Copying Data and Instructions to or from Registers
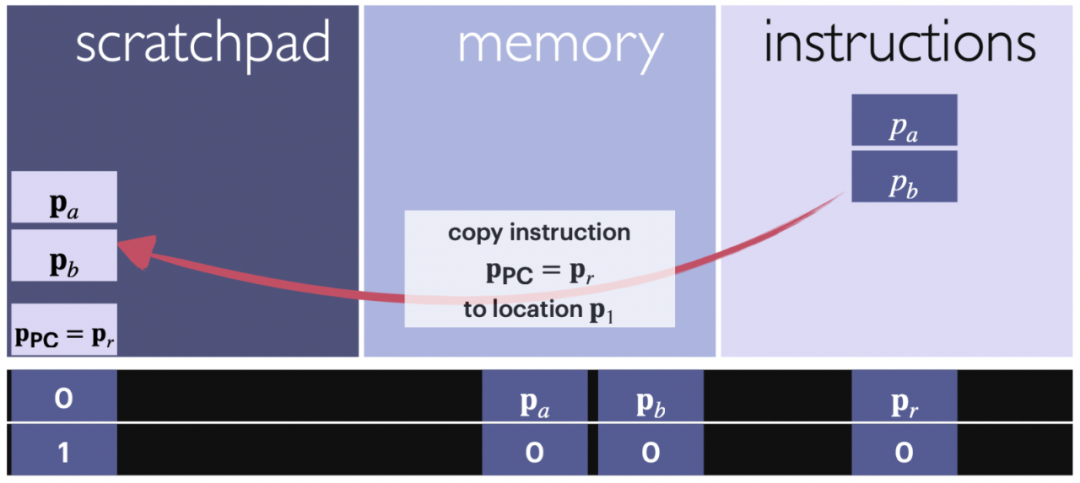
The following lemma illustrates that the command pointed to by the program counter or the data specified in the current command can be copied to the register for further computation. The location of the program counter is typically just below the contents of the register, but can be changed arbitrarily. Keeping it at a specific location throughout the computation helps maintain good organization of the structure.

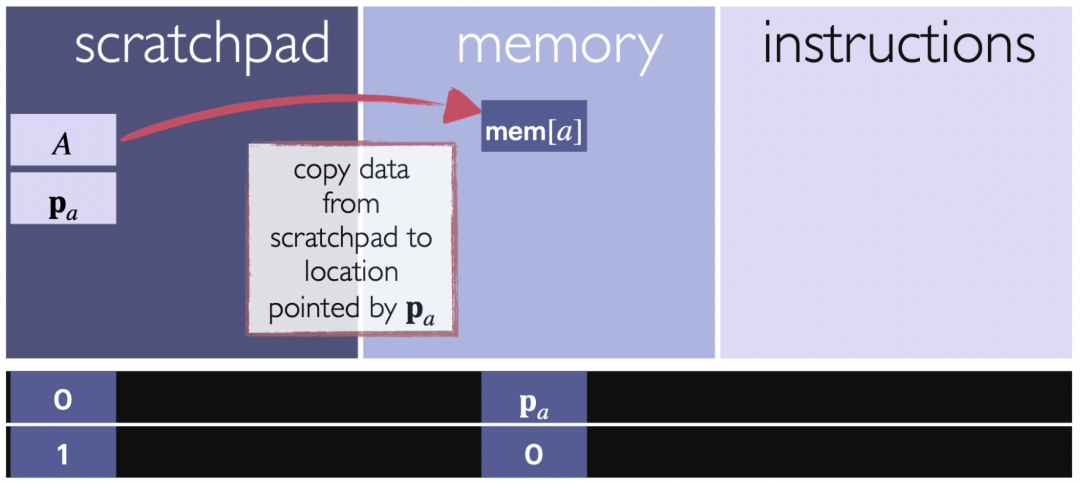
The next lemma explains that the vector v stored in the register can be copied to a specified location in memory, as specified by the register itself. This allows data to be transferred from the register to specific locations in memory for further use or storage.

Conditional Branching
In this section, the authors implement a conditional branch instruction that evaluates a condition and sets the program counter to a specified location if true, or increments the program counter by 1 if false.
The command takes the form: if mem [a] ≤ 0, then go to i, where mem [a] is the value at some location in the memory portion of the input sequence. This command consists of two parts: evaluating the inequality and modifying the program counter.
Simulating a Universal Single Instruction Set Computer
SUBLEQ Transformer
Mavaddat and Parhami demonstrated as early as 1988 that there exists an instruction that any computer program can be converted into a program composed of instances of this instruction. A variant of this instruction is SUBLEQ, which can access different registers or memory locations.
SUBLEQ works simply. It accesses two registers in memory, obtains the difference of their contents, and stores it back in one of the registers, then jumps to a different predefined line of code if the result is negative, or continues executing the next instruction of the current line. Computers built to execute SUBLEQ programs are called single instruction set computers and are universal computers, meaning they are Turing complete if infinite memory is accessible.

The following describes the construction of a looped Transformer that can execute programs written in a specific instruction set. The Transformer tracks code lines, memory locations, and the program counter, using the input memory portion as memory registers and the command portion as code lines/instructions. Registers are used to record additions and pointers involved in each instruction, read, write, conditional branching operations, etc.

FLEQ: A More Flexible Attention-Based Computer
In this section, the authors introduce FLEQ, which is an extension of SUBLEQ, defining a more flexible reduced instruction set computer. This implicit additional instruction set is based on a more advanced version of SUBLEQ, allowing multiple functionalities to be implemented within the same Transformer network. The authors use the term FLEQ to refer to the instructions, language, and the attention-based computer it defines.
The design of FLEQ allows for the implementation of complex algorithms by generating more general functions than simple subtraction, such as matrix multiplication, square root calculations, activation functions, etc.
The attention-based computer executes cycles. In each iteration of the looped Transformer, an instruction is extracted from the instruction set in the input based on the program counter. The instruction is then copied to the register. Depending on the functionality to be achieved, different functional blocks record the results of that functionality locally. Once the result is computed, it is copied back to the specified memory location provided by the instruction.
The execution cycle is similar to that of the single instruction set computer (OISC) described in the previous section, with the main difference being that for each instruction, a selection can be made from a pre-selected list of functions, which are input in arbitrary arrays such as matrices, vectors, and scalars.
Input sequence format. As shown in Figure 6, the input X of the looped Transformer can execute a program composed of a series of FLEQ instructions (X consists of three parts: registers, memory, instructions, etc.).
Format of functional blocks based on Transformer. Each functional block is located in the lower left part of the input X, as shown in Figure 6.
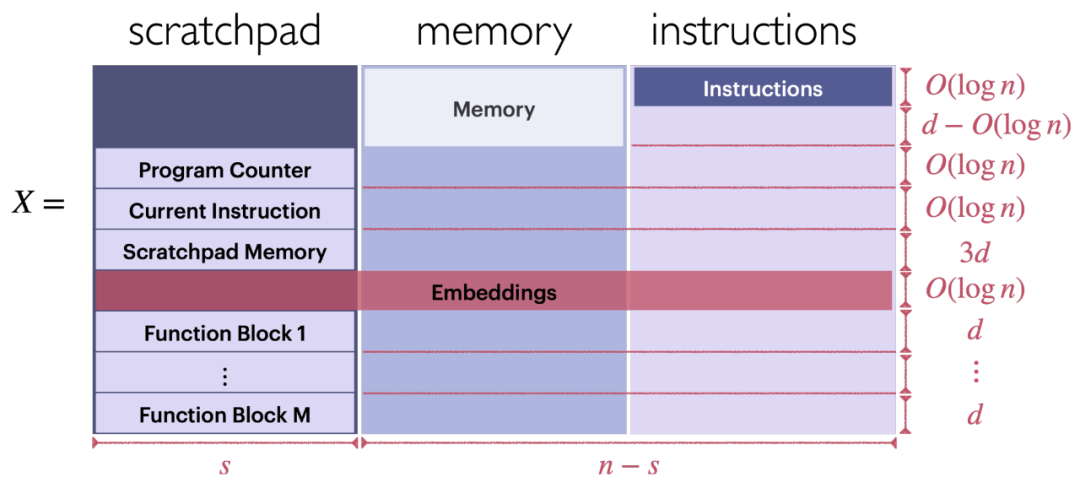
Figure 6: Structure of the input X executing FLEQ commands.
For more technical details and examples, please refer to the original paper.

