Source: Machine Heart
In VGG, U-Net, TCN networks… CNNs are powerful, but they must be customized for specific problems, data types, lengths, and resolutions to perform effectively. One may wonder, can a single CNN be designed to perform well across all these networks?
In this article, researchers from Vrije Universiteit Amsterdam, University of Amsterdam, and Stanford University propose CCNN, a single CNN that can achieve SOTA across multiple datasets (e.g., LRA)!
In 1998, LeCun et al. proposed Convolutional Neural Networks (CNN), a class of deep learning models widely used in machine learning. Due to the high performance and efficiency of CNNs, they achieve SOTA performance across multiple applications involving cross-sequence, vision, and high-dimensional data. However, CNNs (and neural networks in general) have a significant flaw; these architectures must be customized for specific applications to handle different data lengths, resolutions, and dimensions.This, in turn, leads to a plethora of task-specific CNN architectures.
Data can vary widely in length; for example, images can be 32×32 or 1024×1024. The problem with standard CNNs is that their convolutional kernels are local, requiring a carefully selected stride and pooling layer tailored for each length to capture the entire context in a custom architecture. Furthermore, many data types are inherently continuous, possessing the same semantic meaning at different resolutions; for instance, images can be captured at any resolution and retain the same semantic content, and audio can be sampled at 16kHz or 44.1kHz, yet still sound the same to the human ear.
However, due to the discreteness of convolutional kernels, traditional CNNs cannot be used across resolutions. When considering data of different dimensions with the same CNN, these two issues are exacerbated; for example, sequences (1D), vision (2D), and high-dimensional data (3D, 4D) operate at different feature lengths and resolutions, such as the length of one second of audio easily reaching 16000, which starkly contrasts the image sizes in benchmark datasets.
In this article, researchers propose a step towards a universal CNN architecture. The goal is to construct a single CNN architecture that can be used for data of arbitrary resolutions, lengths, and dimensions. Standard CNNs require task-specific architectures because the discreteness of their convolutional kernels binds the kernels to specific data resolutions, and due to the large number of parameters needed to construct large discrete convolutional kernels, they are not suitable for modeling global context.
Thus, to construct a universal CNN architecture, the key is to develop a resolution-agnostic convolutional layer that can model long-range dependencies in a parameter-efficient manner. This research was selected for ICML 2022.
Paper link:
https://arxiv.org/pdf/2206.03398.pdf
Code link:
https://github.com/david-knigge/ccnn
Contributions of this article
-
This research proposes Continuous CNN (CCNN): a simple, universal CNN that can be used across data resolutions and dimensions without structural modifications. CCNN outperforms SOTA on tasks involving sequences (1D), vision (2D), and irregularly sampled data with varying test-time resolutions.
-
This research provides several improvements to existing CCNN methods, enabling them to match current SOTA methods like S4. Major improvements include the initialization of the kernel generator network, modifications to the convolutional layers, and overall structure of the CNN.
Continuous Kernel Convolution
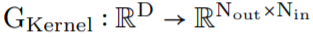as a kernel generator network while parameterizing the convolutional kernels as continuous functions. This network maps coordinates
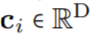to the convolutional kernel values at that position:
(Figure 1a). By passing a vector of K coordinates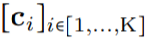
through G_Kernel, a convolutional kernel K of the same size can be constructed, i.e.,
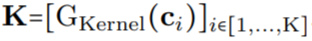. Subsequently, a convolution operation is performed between the input signal
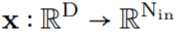and the generated convolutional kernel
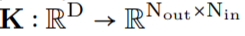to construct the output feature representation
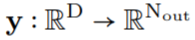, i.e.,
.
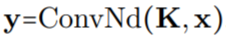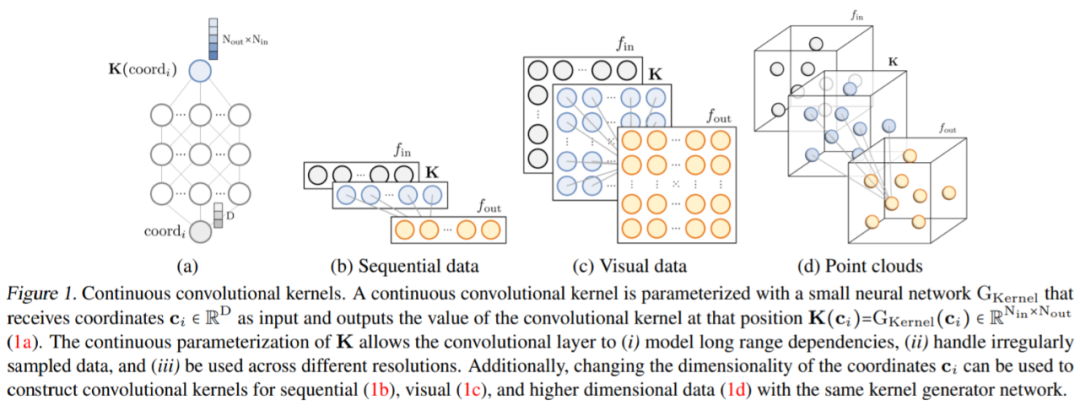
General operation for arbitrary data dimensions. By changing the dimensionality D of the input coordinates c_i, the kernel generator network G_Kernel can be used to construct convolutional kernels of arbitrary dimensions. Therefore, the same operation can be used to handle sequences D=1, vision D=2, and higher-dimensional data D≥3.
Equivalent responses for different input resolutions. If the input signal x has a resolution change, such as audio initially observed at 8KHz now observed at 16KHz, convolving with discrete convolutional kernels will yield different responses, as the kernels will cover different subsets of the input at each resolution. In contrast, continuous kernels are resolution-agnostic and can recognize inputs regardless of the input’s resolution.
When presented with input at different resolutions (e.g., higher resolution), it is sufficient to pass a finer coordinate grid through the kernel generator network to construct the same kernel at the corresponding resolution. For signals x sampled at resolutions r (1) and r (2) and continuous convolutional kernels K, the convolutions at the two resolutions are approximately equal to a factor proportional to the resolution change:
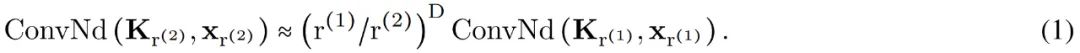
CCNN: Modeling Long-Range Dependencies in ND
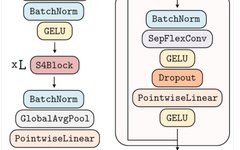
Improvements to residual blocks with continuous kernel convolution. This research modifies the FlexNet architecture, where the residual network consists of blocks similar to the S4 network. The CCNN architecture is shown in Figure 2 below.
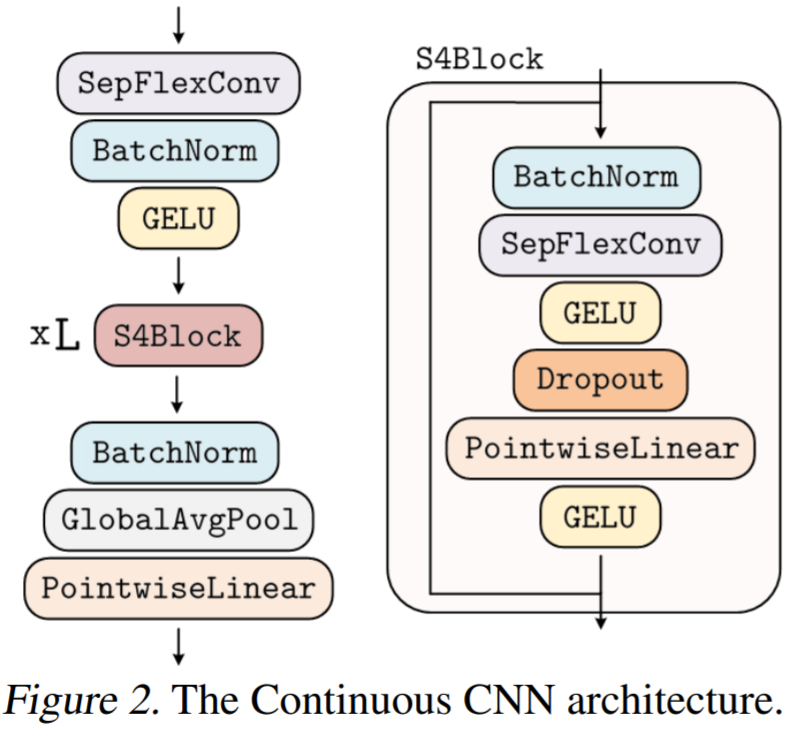
Based on these observations, this research constructs a depth-wise separable version of FlexConv, where channel-wise convolutions are computed using kernels generated by the kernel generator network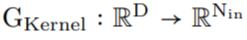
, followed by point-wise convolutions from N_in to N_out. This modification allows for constructing a broader CCNN—from 30 to 110 hidden channels—without increasing network parameters or computational complexity.
Correct initialization of the kernel generator network G_Kernel. This research observed that previous studies did not correctly initialize the kernel generator network. Before initialization, it is desired that the variance of the input and output of the convolutional layer remains equal to avoid gradient explosion and vanishing, i.e., Var (x)=Var (y). Thus, the convolutional kernels were initialized to have variance Var (K)=gain^2 /(in channels ⋅ kernel size), where the gain depends on the nonlinearity used.
However, the initialization of the neural network preserves the unitary variance of the input in the output. Therefore, when used as a kernel generator network, the standard initialization method results in kernels having unitary variance, i.e., Var (K)=1. As a result, CNNs using neural networks as kernel generator networks experienced a layer-wise increase in feature representation variance proportional to channel ⋅ kernel size. For instance, researchers observed that CKCNNs and FlexNets had logits of about 1e^19 at initialization. This is undesirable as it may lead to training instability and necessitate low learning rates.
To address this issue, this research requires G_Kernel to output variance equal to gain^2 /(in_channels⋅kernel_size) instead of 1. They achieved this by re-weighting the last layer of the kernel generator network. Thus, the variance of the output from the kernel generator network follows the initialization of traditional convolutional kernels, and the logits of CCNN present unitary variance at initialization.
Experimental Results
As shown in Tables 1-4, the CCNN model performs well across all tasks.
First, the 1D image classification CCNN achieves SOTA on multiple continuous benchmarks such as Long Range Arena, speech recognition, and 1D image classification, all within a single architecture. CCNN typically has a simpler architecture with fewer parameters than other model methods.
Next, for 2D image classification: through a single architecture, CCNN can match and surpass deeper CNNs.
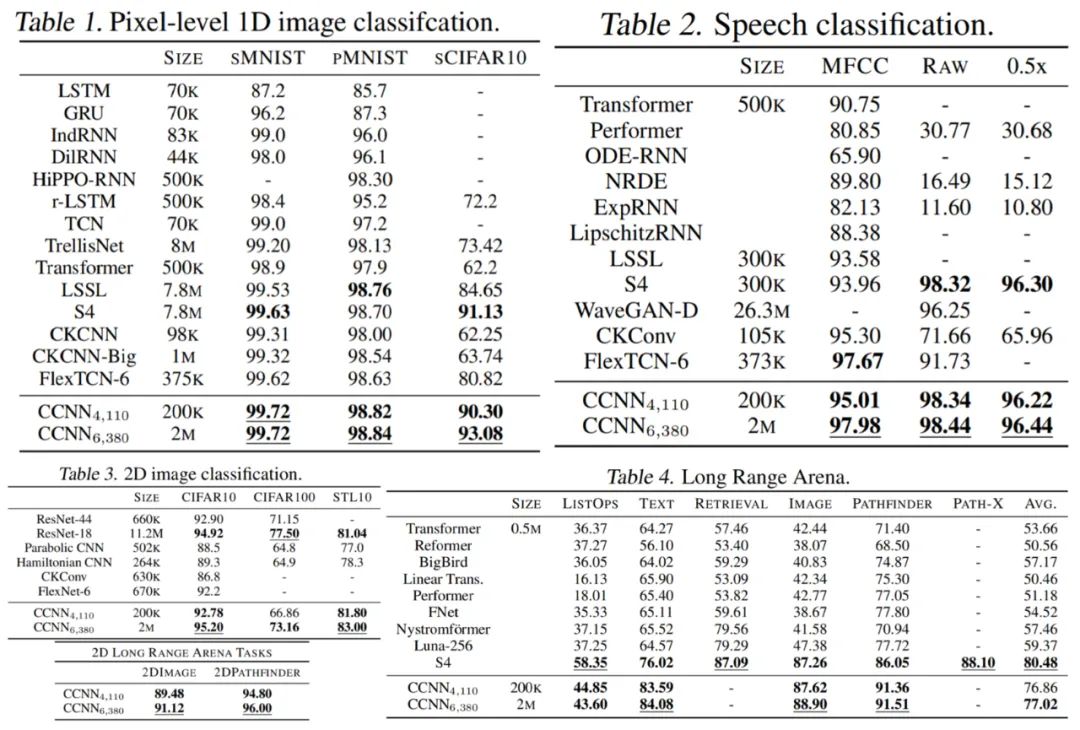
The importance of modeling long-range dependencies in ND. In principle, all tasks can be viewed as sequence tasks without considering the 2D structure; this research can easily define CCNN in multi-dimensional space by merely changing the dimensionality of the coordinates entering the kernel generator network. Interestingly, this research observed that considering the 2D characteristics of images and Pathfinder tasks in the LRA benchmark yielded better results (see Table 3).
In the PathFinder with 2D images, the largest CCNN achieved an accuracy of 96.00%, nearly 10 points higher than the previous SOTA, and performed significantly better than CCNN on flat images.
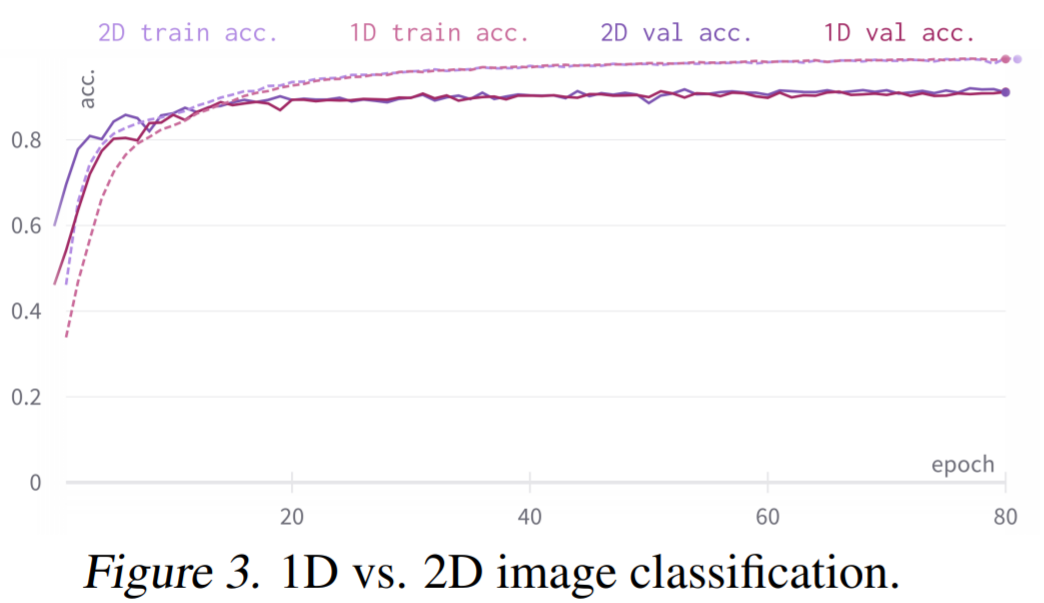
Moreover, models trained on original 2D data exhibited faster convergence than their sequential counterparts (Figure 3). 2D CNNs with small convolutional kernels, such as ResNet-18, fail to resolve Pathfinder due to a lack of fine-grained global context modeling from intermediate pooling layers.
Editor: Yu Tengkai
Proofreader: Lin Yilin
