Vector distances are crucial in various fields such as mathematics, physics, engineering, and computer science. They are used to measure physical quantities, analyze data, identify similarities, and determine relationships between vectors. This article will provide an overview of vector distances and their applications in data science.
What Is Vector Distance?
Vector distance, also known as distance metric or similarity metric, is a mathematical function used to quantify the similarity or dissimilarity between two vectors. These vectors can represent various datasets, and vector distance helps to understand how close or far apart the vectors are in the feature space. Therefore, vector distance is essential in various machine learning algorithms, enabling these algorithms to make decisions based on the relationships between vectors.
For distance measurement, we can choose between geometric distance measures and statistical distance measures, depending on the type of data. Features may have different data types (e.g., real values, boolean values, categorical values), and the data may be multidimensional or consist of geospatial data.
What Are the Applications of Vector Distance in Machine Learning?
Never underestimate the power of vector distance. Vector distance has a wide range of applications in the field of machine learning.
Firstly, in clustering tasks, vector distance helps to group similar vectors into clusters. Algorithms such as k-means, hierarchical clustering, and DBSCAN rely on vector distance to determine which vectors belong to the same cluster.
In classification tasks, algorithms like kNN classification determine the classification of a vector by calculating its distance to its k nearest neighbor vectors, thereby assigning the vector to the cluster with the most neighbors. In Natural Language Processing (NLP), vector distance is used to compute document similarity, perform sentiment analysis, and cluster text documents.
In data preprocessing steps, vector distance is crucial for feature scaling, normalization, and outlier removal, ensuring that data can better fit machine learning algorithms.
In neural network training, vector distance serves as a loss function or regularization term, encouraging a certain relationship to be maintained between the output vector and the target vector, thus improving model performance. In anomaly detection tasks, measuring the distance between a vector and the center cluster or other vectors can detect anomalies or outliers, as these vectors are considered anomalies due to their distance from the majority of vectors.
Dimensionality reduction techniques such as UMAP and t-SNE utilize vector distance to create low-dimensional representations of high-dimensional data while preserving pairwise distances as much as possible, aiding in data visualization and understanding.
In summary, vector distance is the cornerstone of many machine learning tasks and applications, and choosing the appropriate vector distance is crucial for the algorithm’s ability to capture the relationships between vector data.
What Are the Types of Vector Similarity?
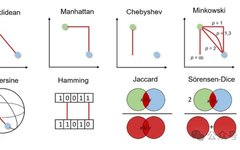
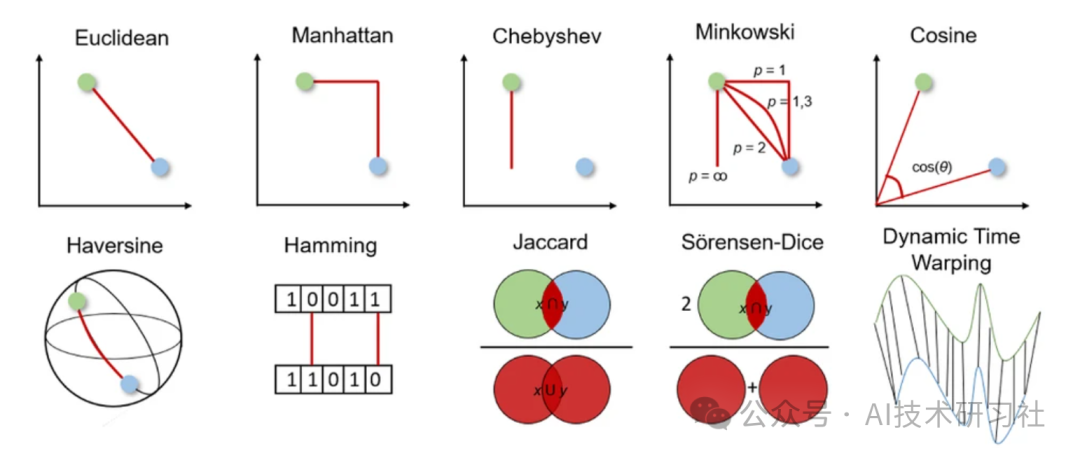
1. Euclidean Distance
Euclidean distance measures the shortest distance between two real-valued vectors. Due to its intuitiveness, ease of use, and good results for many use cases, it is the most commonly used distance metric and the default distance metric for many applications.
Euclidean distance is also known as the l2 norm, calculated as follows:
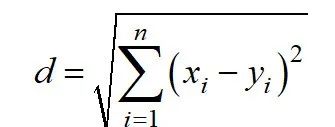
Python code is as follows:
from scipy.spatial import distance
distance.euclidean(vector_1, vector_2)Euclidean distance has two main drawbacks. First, the distance measurement is not suitable for data in dimensions higher than 2D or 3D space. Second, if we do not normalize and/or standardize the features, the distance may be skewed due to differences in units.
2. Manhattan Distance
Manhattan distance is also known as taxi or city block distance because the distance between two real-valued vectors is calculated based on the assumption that one can only move at right angles. This distance metric is often used for discrete and binary attributes, as it provides a true path.
Manhattan distance is based on the l1 norm, calculated as follows:
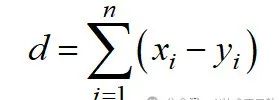
Python code is as follows:
from scipy.spatial import distance
distance.cityblock(vector_1, vector_2)Manhattan distance has two main drawbacks. It is not as intuitive as Euclidean distance in high-dimensional space, and it does not show the possible shortest path. While this may not be an issue, we should be aware that this is not the shortest distance.
3. Chebyshev Distance
Chebyshev distance is also known as chessboard distance because it is the maximum distance between two real-valued vectors in any dimension. It is commonly used in warehouse logistics, where the longest path determines the time required to get from one point to another.
Chebyshev distance is calculated using the l-infinity norm:
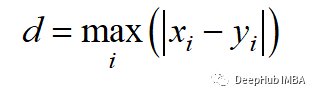
Python code is as follows:
from scipy.spatial import distance
distance.chebyshev(vector_1, vector_2)Chebyshev distance has very specific use cases, so it is rarely used.
4. Minkowski Distance
Minkowski distance is a generalization of the distances mentioned above. It can be used for the same use cases while providing high flexibility. We can choose the p value to find the most suitable distance metric.
Minkowski distance is calculated as follows:
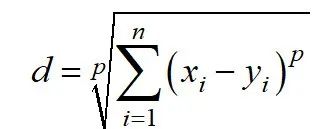
Python code is as follows:
from scipy.spatial import distance
distance.minkowski(vector_1, vector_2, p)Since Minkowski distance represents different distance metrics, it shares the same main drawbacks as them, such as issues in high-dimensional space and dependency on feature units. Additionally, the flexibility of the p value can also be a drawback, as it may reduce computational efficiency since finding the correct p value requires multiple calculations.
5. Cosine Similarity and Distance
Cosine similarity measures direction, determined by the cosine of the angle between two vectors, and ignores the size of the vectors. Cosine similarity is often used in high dimensions where the size of the data is not important, such as in recommendation systems or text analysis.
Cosine similarity can range between -1 (opposite direction) and 1 (same direction), calculated as follows:
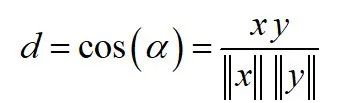
Cosine similarity is commonly used in positive space ranging from 0 to 1. Cosine distance is simply 1 minus cosine similarity, which lies between 0 (similar) and 1 (dissimilar).
Python code is as follows:
from scipy.spatial import distance
distance.cosine(vector_1, vector_2)The main drawback of cosine distance is that it does not consider size but only the direction of the vectors. Thus, it does not fully account for the differences in values.
6. Haversine Distance
Haversine distance measures the shortest distance between two points on the surface of a sphere. It is commonly used in navigation, where longitude and latitude and curvature affect the calculations.
The formula for Haversine distance is as follows:
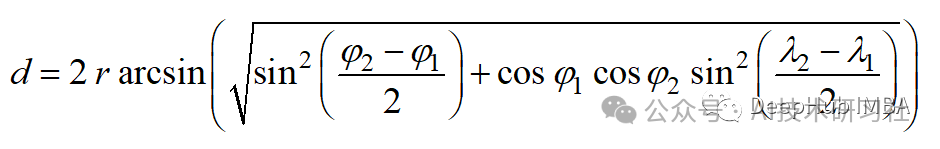where r is the radius of the sphere, φ and λ are the longitude and latitude.
Python code is as follows:
from sklearn.metrics.pairwise import haversine_distances
haversine_distances([vector_1, vector_2])The main drawback of Haversine distance is the assumption of a spherical shape, which rarely occurs.
7. Hamming Distance
Hamming distance measures the difference between two binary vectors or strings.
It compares the vectors element-wise and averages the number of differences. If two vectors are the same, the resulting distance is 0; if two vectors are completely different, the resulting distance is 1.
Python code is as follows:
from scipy.spatial import distance
distance.hamming(vector_1, vector_2)Hamming distance has two main drawbacks. The distance measurement can only compare vectors of the same length, and it cannot provide the magnitude of the differences. Therefore, it is not recommended to use Hamming distance when the magnitude of differences is important.
Statistical distance measures can be used for hypothesis testing, goodness-of-fit testing, classification tasks, or outlier detection.
8. Jaccard Index and Distance
The Jaccard index is used to determine the similarity between two sample sets. It reflects how many one-to-one matches exist compared to the entire dataset. The Jaccard index is often used for binary data, such as comparing predictions from deep learning models in image recognition with labeled data, or comparing text patterns in documents based on word overlap.
The Jaccard distance is calculated as follows:
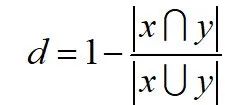
Python code is as follows:
from scipy.spatial import distance
distance.jaccard(vector_1, vector_2)The main drawback of the Jaccard index and distance is that it is strongly influenced by the scale of the data, meaning the weight of each item is inversely proportional to the size of the dataset.
9. Sørensen-Dice Index
The Sørensen-Dice index is similar to the Jaccard index, measuring the similarity and diversity of sample sets. This index is more intuitive as it calculates the percentage of overlap. The Sørensen-Dice index is commonly used in image segmentation and text similarity analysis.
The calculation formula is as follows:
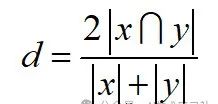
Python code is as follows:
from scipy.spatial import distance
distance.dice(vector_1, vector_2)The main drawback is also that it is significantly affected by the size of the dataset.
Popular Software Libraries for Using Vector Distances
Applications of Faiss Vector Retrieval Library
Faiss is an efficient vector retrieval library developed by the Facebook AI research team, widely used for similarity search and clustering of high-dimensional vectors. Here are some common operations of Faiss:
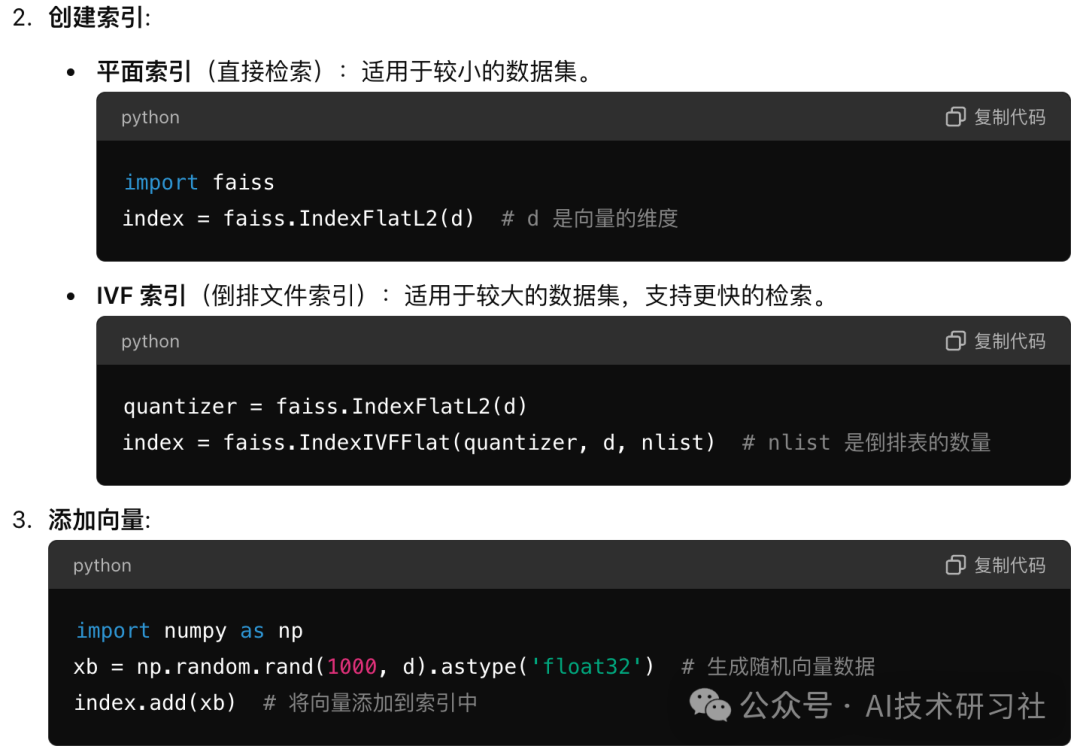
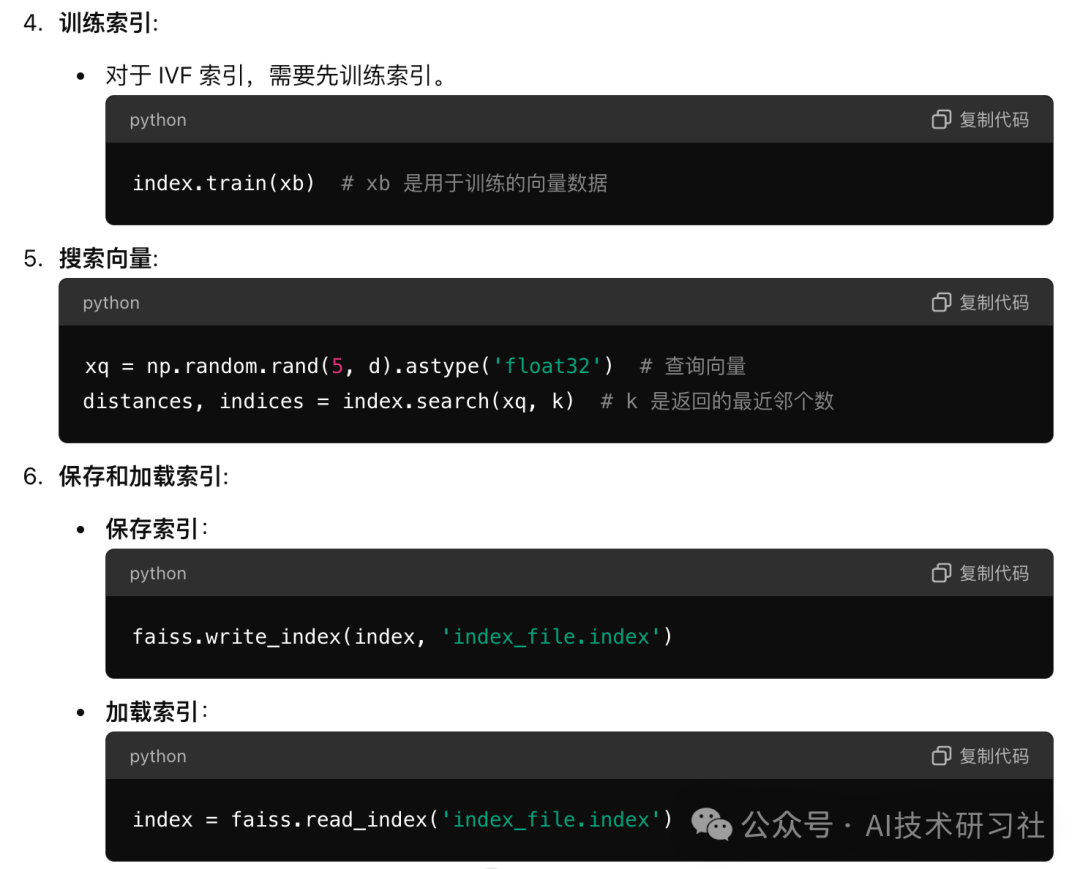
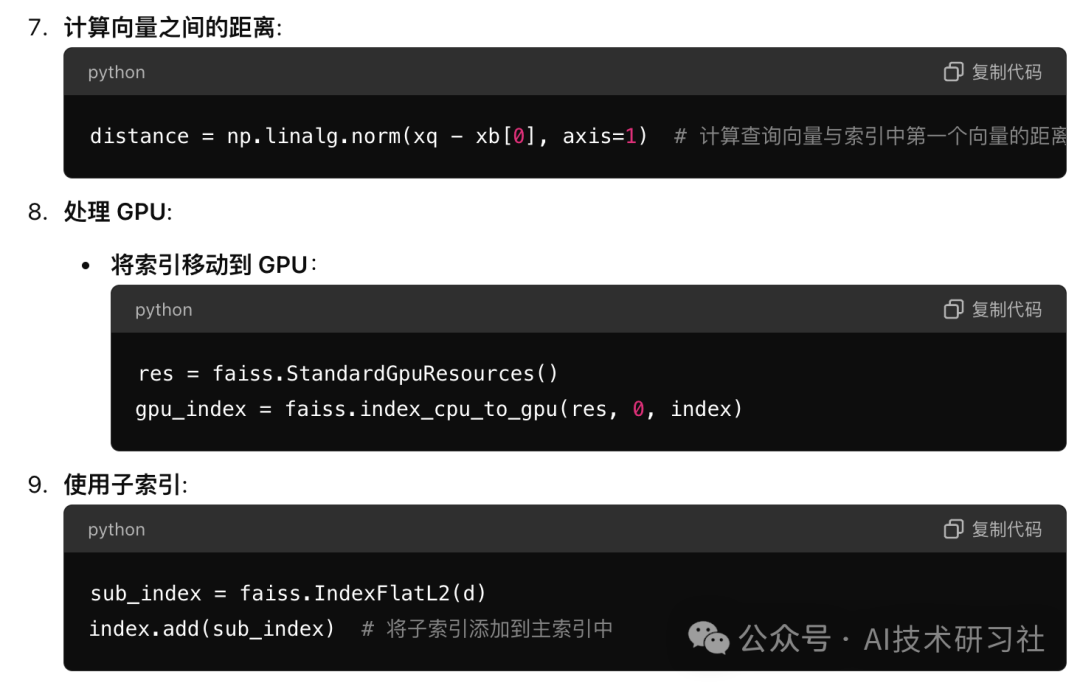
These operations cover the basic use cases of Faiss, including creating indexes, adding and searching vectors, and compatibility with GPUs. Depending on the actual application requirements, you can choose the appropriate index type and optimization method.
Overall, the value of vector database distances lies in their core role in efficient retrieval and processing of large-scale data.
By quantifying the similarity or dissimilarity between vectors, vector distances enable machine learning algorithms to accurately classify, cluster, and predict data in feature space. It not only enhances the accuracy in fields such as Natural Language Processing, image recognition, and anomaly detection, but also plays a key role in data preprocessing and dimensionality reduction processes.
Vector distance is a foundational tool for achieving intelligent data analysis and decision-making, greatly advancing AI and machine learning technologies.
References:
-
https://zilliz.com.cn/glossary/%E5%90%91%E9%87%8F%E8%B7%9D%E7%A6%BB
-
https://segmentfault.com/a/1190000042705356