XGBoost (eXtreme Gradient Boosting) has become quite popular in various competitions in recent years due to its excellent predictive performance. Below, we will introduce its principles.
Principle
First, we need to understand that XGBoost is an improvement of the GBDT algorithm.

During the k-th iteration, the loss function of GBDT can be denoted as L(y,F[k](x)). Its second-order Taylor expansion at F[k-1](x) is given by
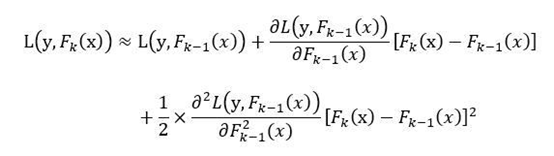
According to the forward distribution algorithm, we have
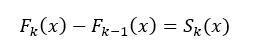
Substituting this into the previous loss function, letting a equal the first derivative and b equal the second derivative, the loss function can be expressed as
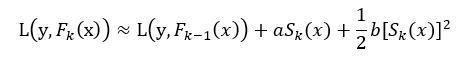
Where, a and b are
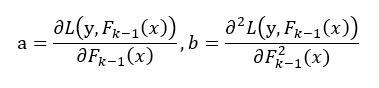
Thus, for all samples, the loss function is
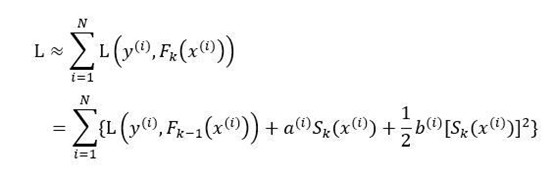
Optimizing the above expression is equivalent to optimizing
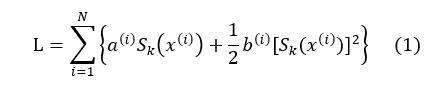
The specific reason has been discussed when introducing the AdaBoost algorithm, so we will not elaborate here.
Regularization
To prevent overfitting, we often need to add a regularization term when optimizing the loss function.
Then, the loss function with the regularization term added is
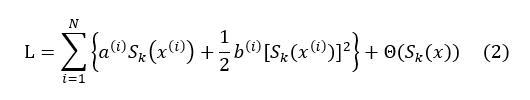
In the previous article, we introduced
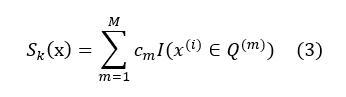
And the regularization term is constructed by the following formula
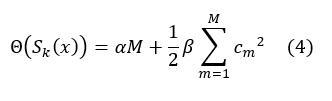
Where, M is the number of leaf nodes, and α and β are parameters of the regularization term used to control the complexity of the model.
Substituting (3) and (4) into (2), we get
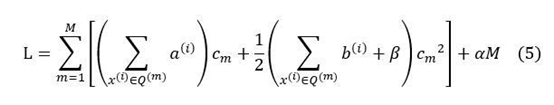
To find the minimum of (5), we need to take the partial derivative of c[m], that is
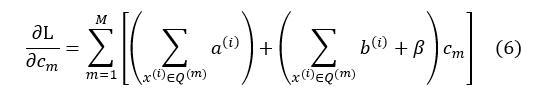
Then set (6) to 0, we get
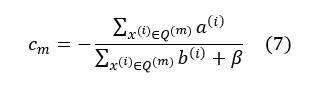
Next, we substitute (7) back into (5) to obtain the loss function L as
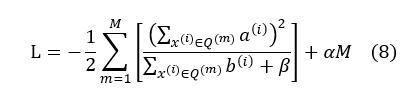
(8) is the loss function obtained in the k-th round.
Looking back at the entire process, we find that XGBoost is essentially about performing a second-order Taylor expansion of the loss function to obtain a solution, and then substituting it back into the loss function. In other words, it uses this solution to help construct the decision trees, thereby minimizing the residuals and achieving optimal model performance.
UA Academy is enrolling! Students who want to build foundational capabilities in the AI era, please pay attention!
