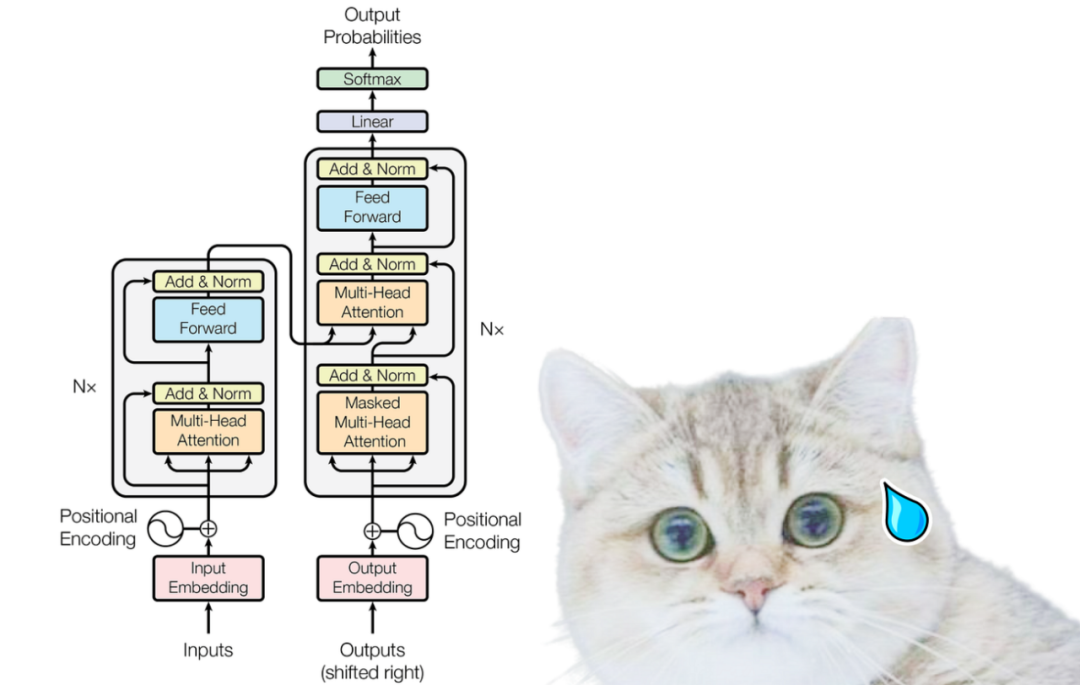
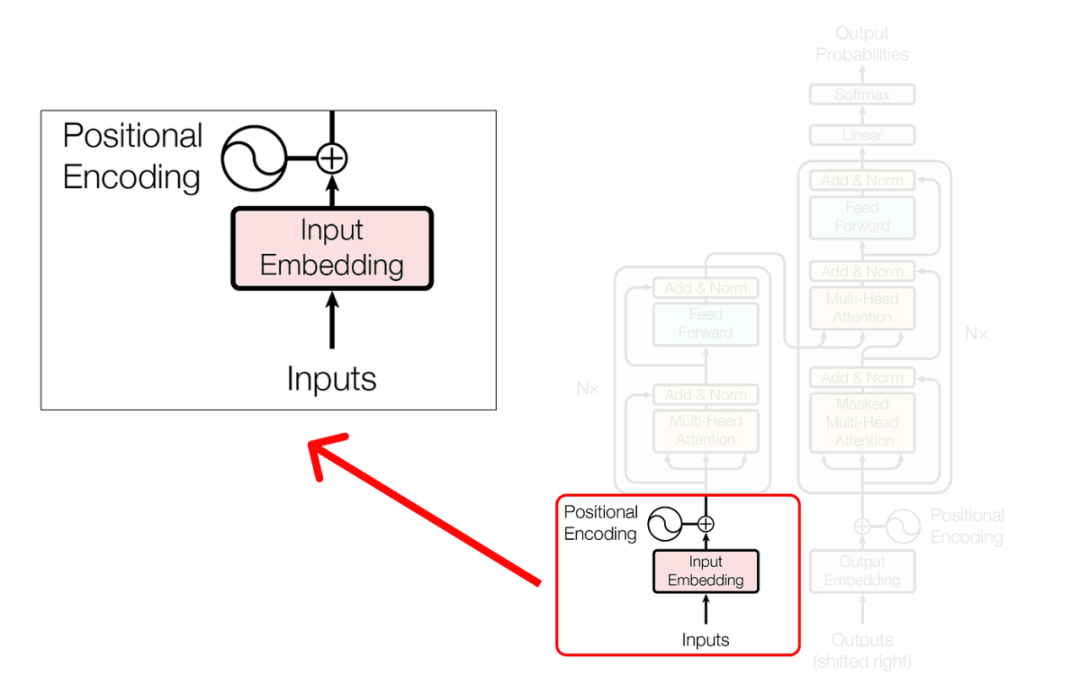
Inputs and Positional Encoding

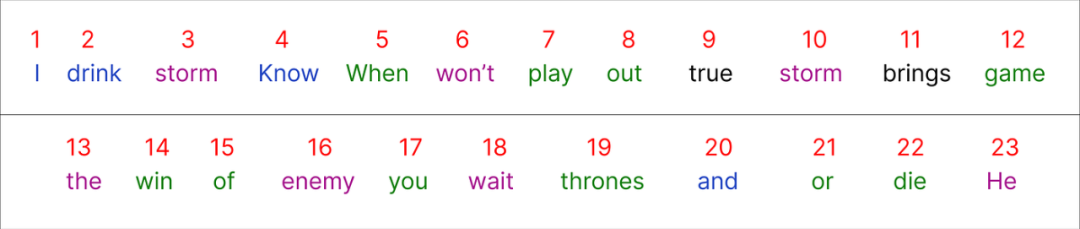
Step 1 (Defining the Data)

Step 2 (Finding the Vocab Size)

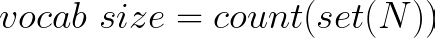




Step 3 (Encoding and Embedding)


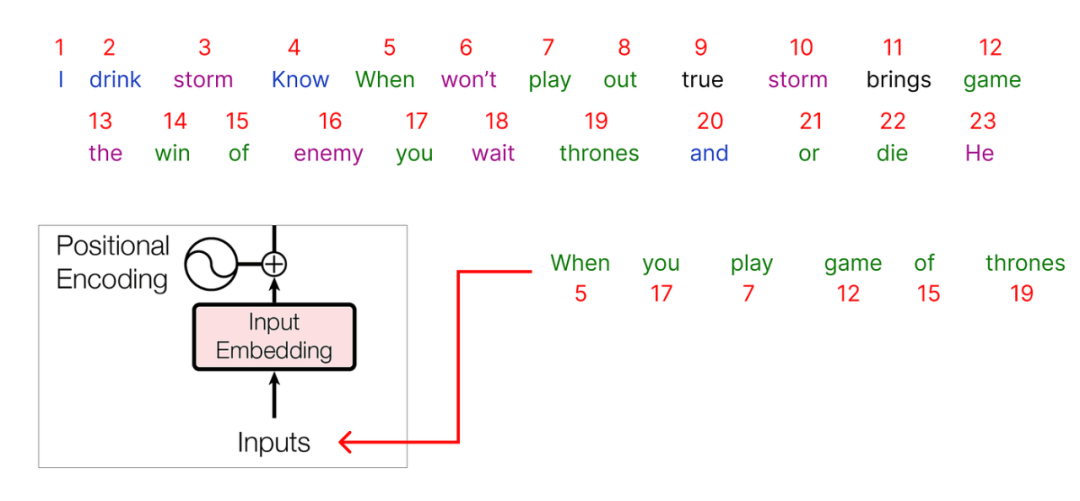

-
These embeddings can be found using Google Word2Vec (vector representation of words). In our numerical example, we will assume that the embedding vector for each word is filled with random values between (0 and 1).
-
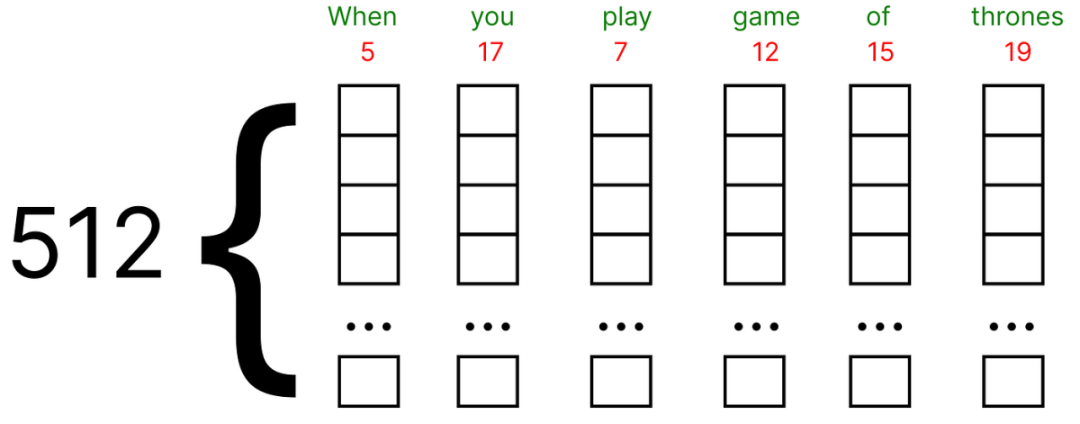
Additionally, the original paper uses an embedding vector of 512 dimensions, while we will consider a very small dimension of 5 for the numerical example.

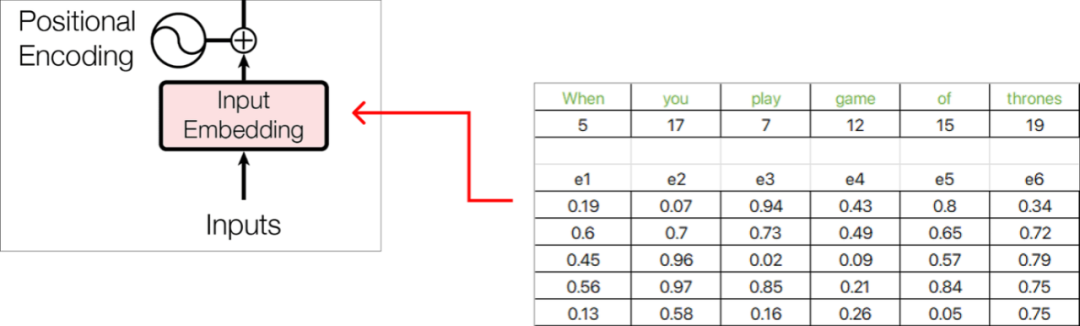
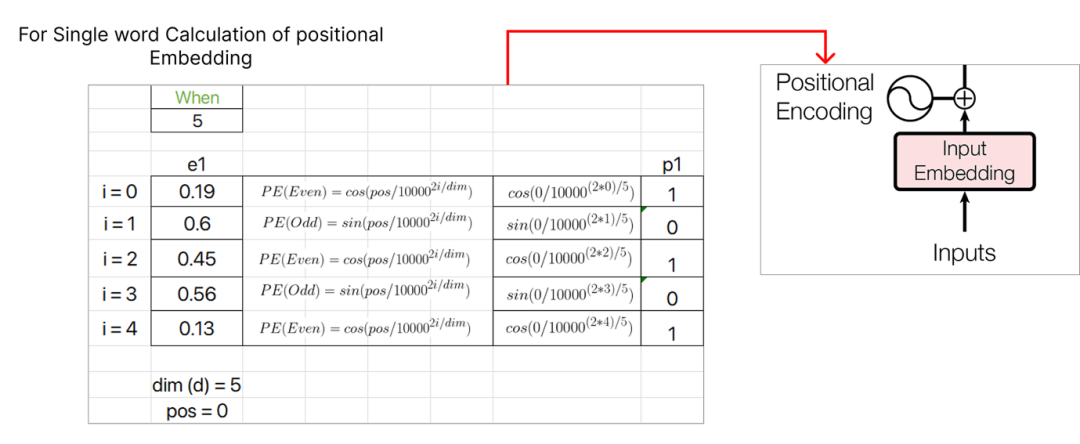
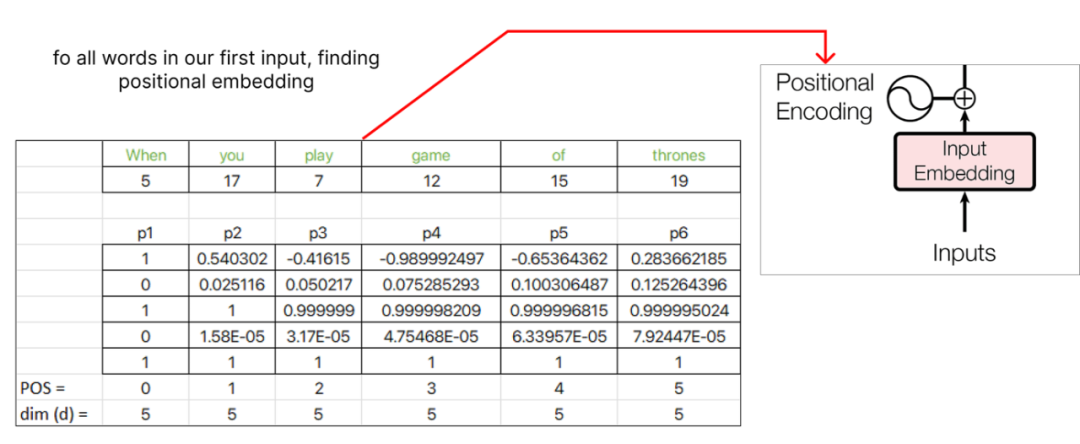
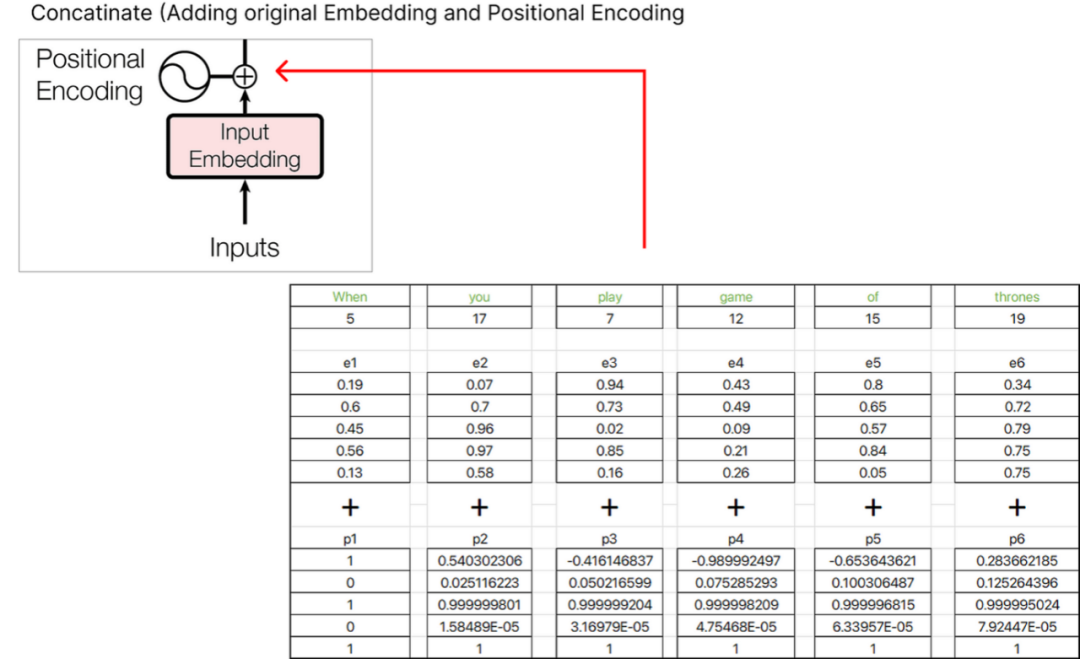
Step 4 (Positional Embedding)
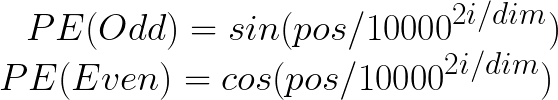



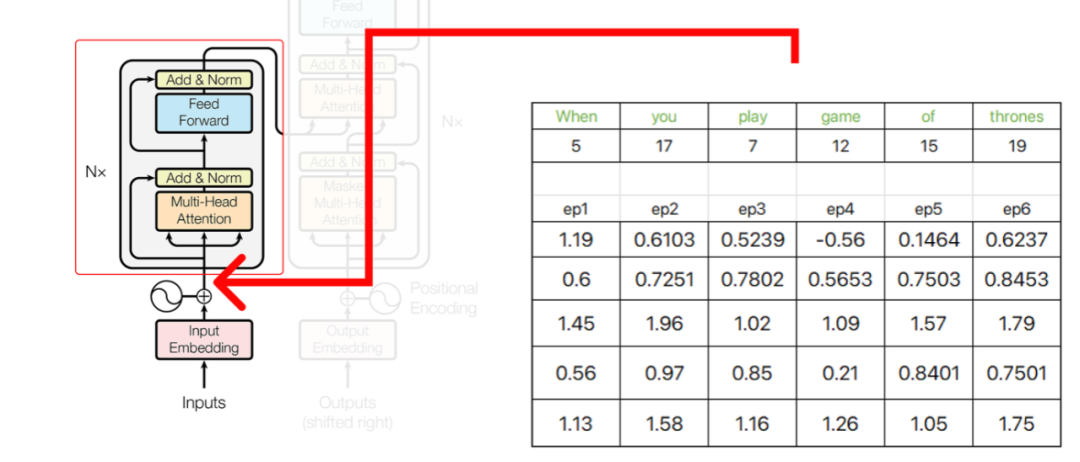

Encoder

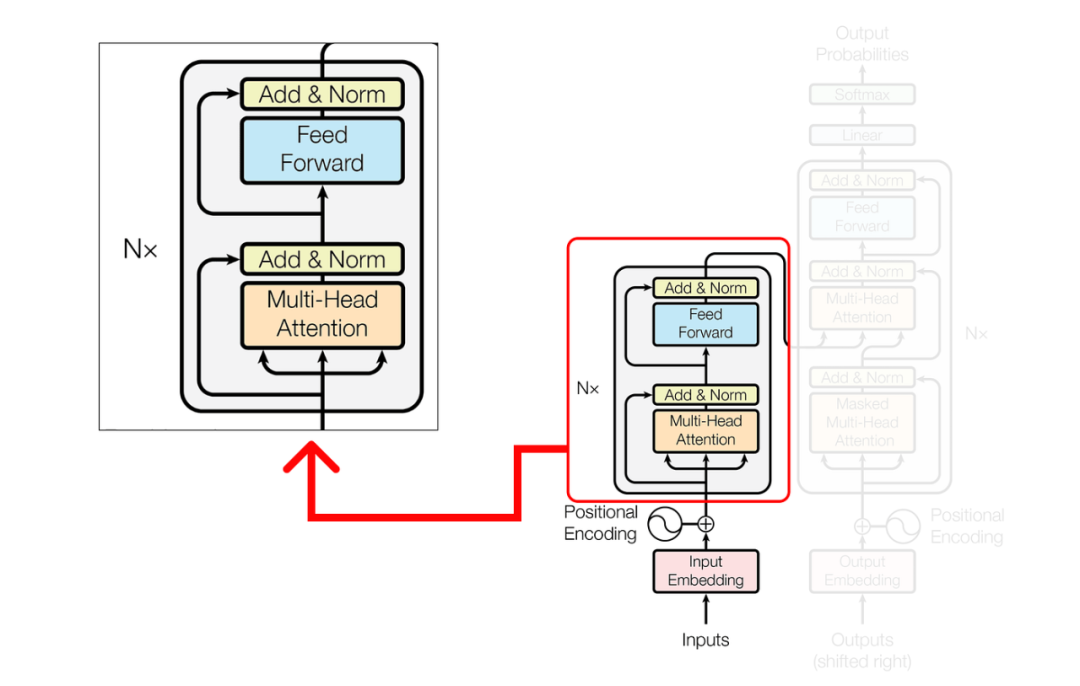

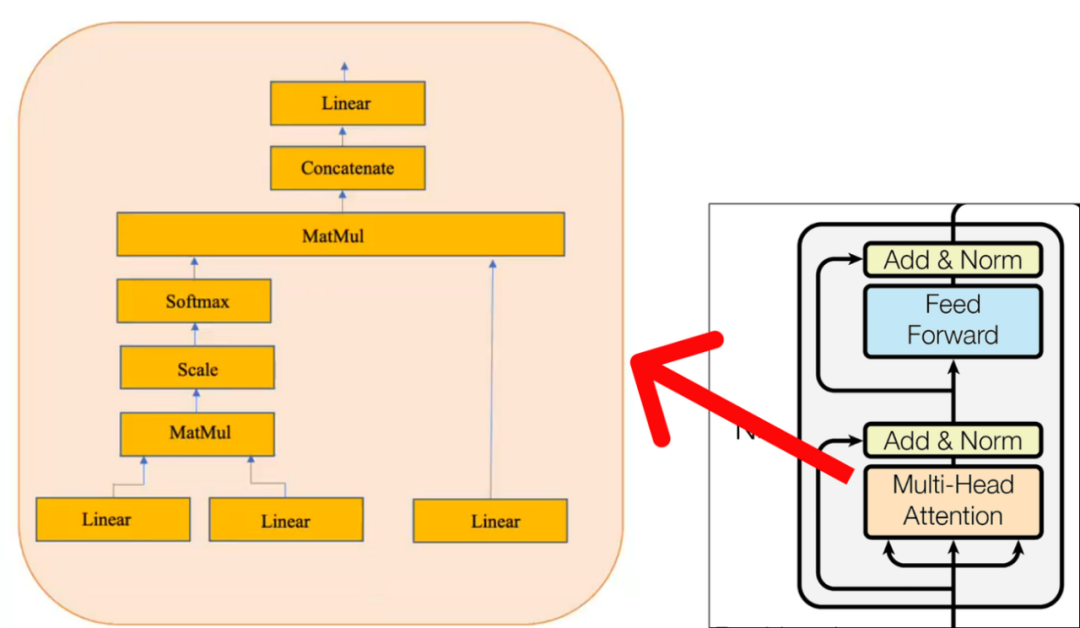
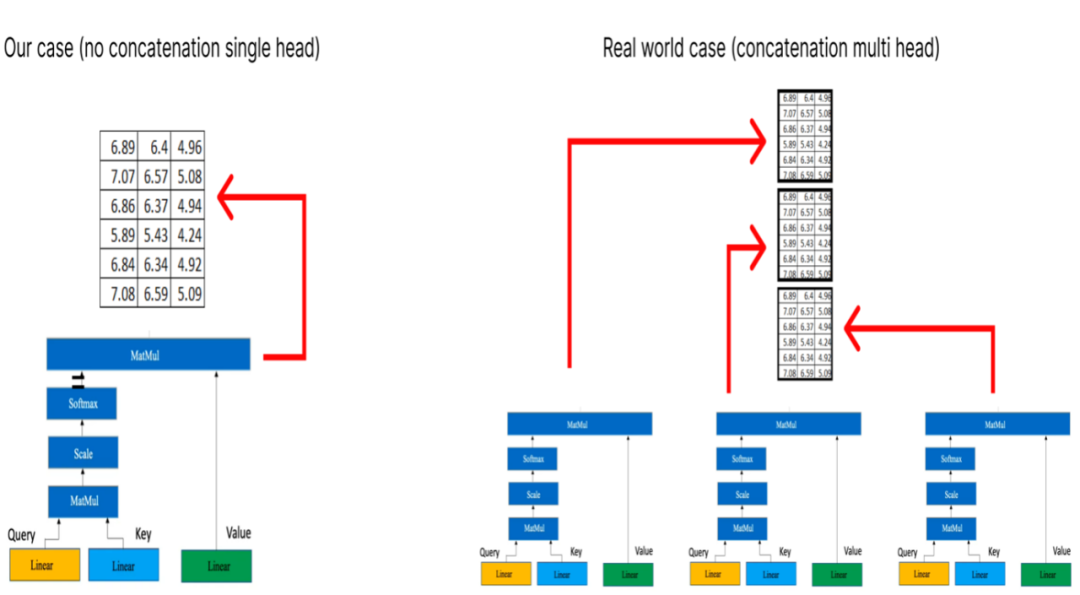
Step 1 (Performing Single Head Attention)
-
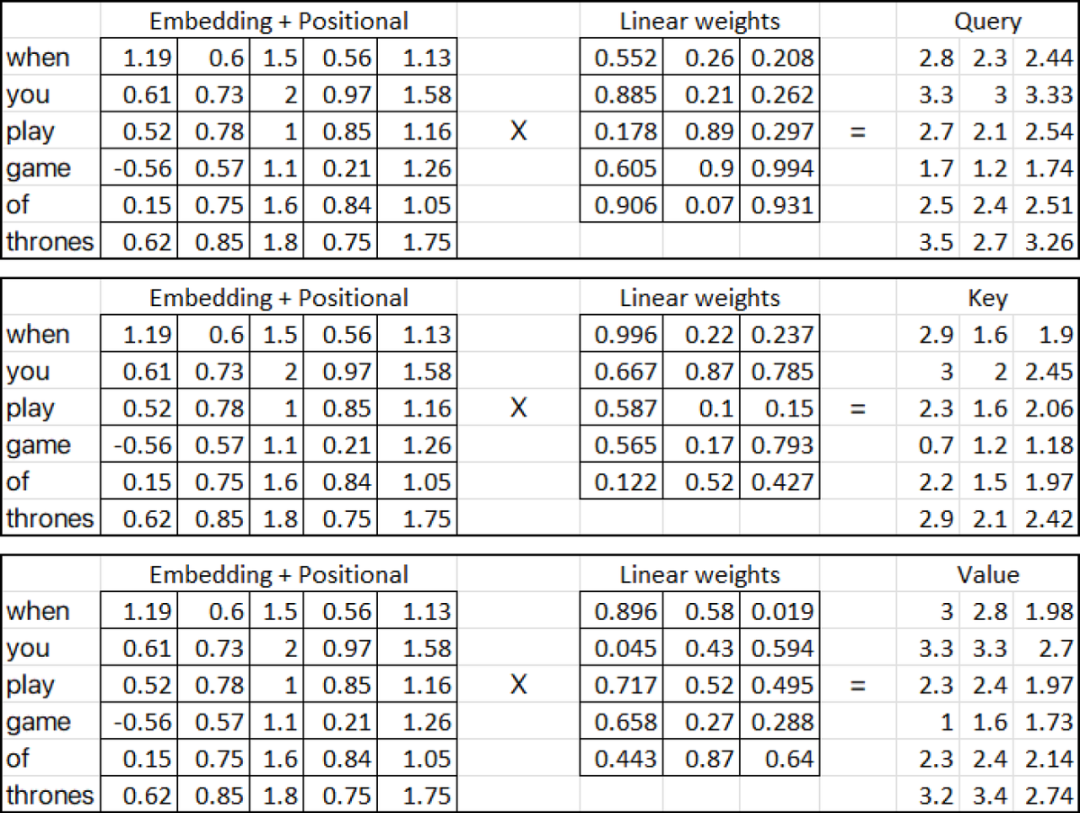
Query
-
Key
-
Value





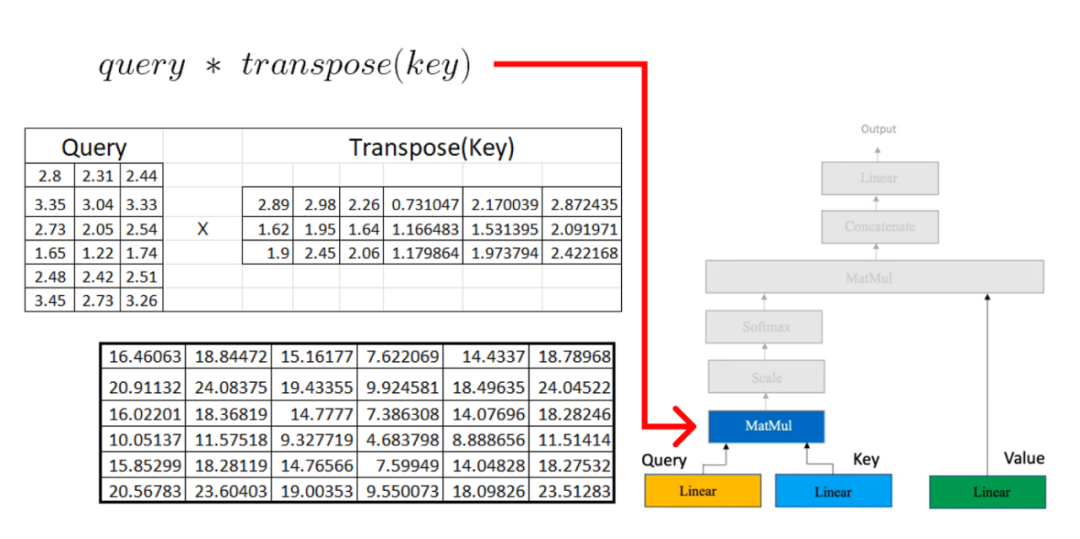
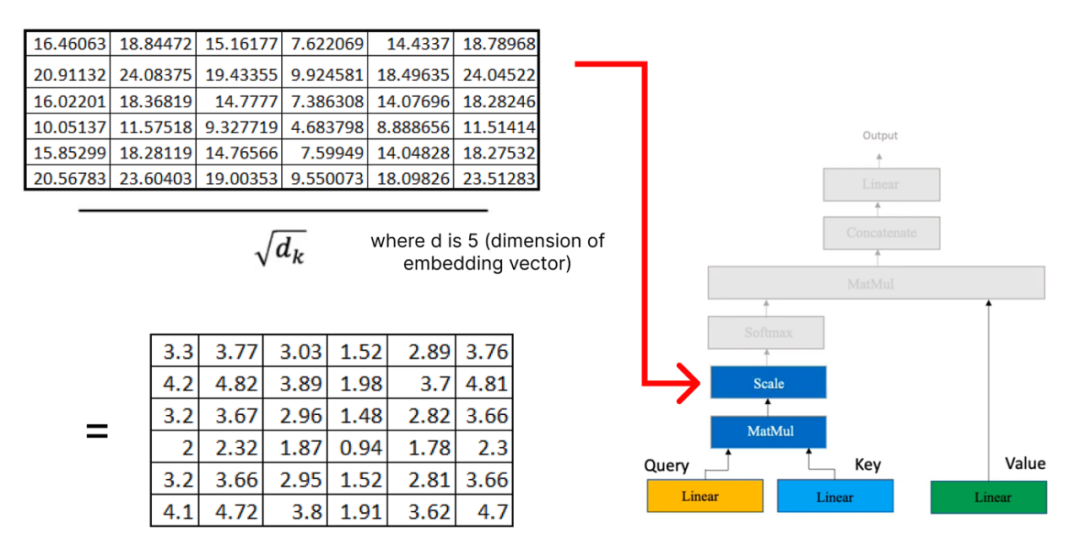

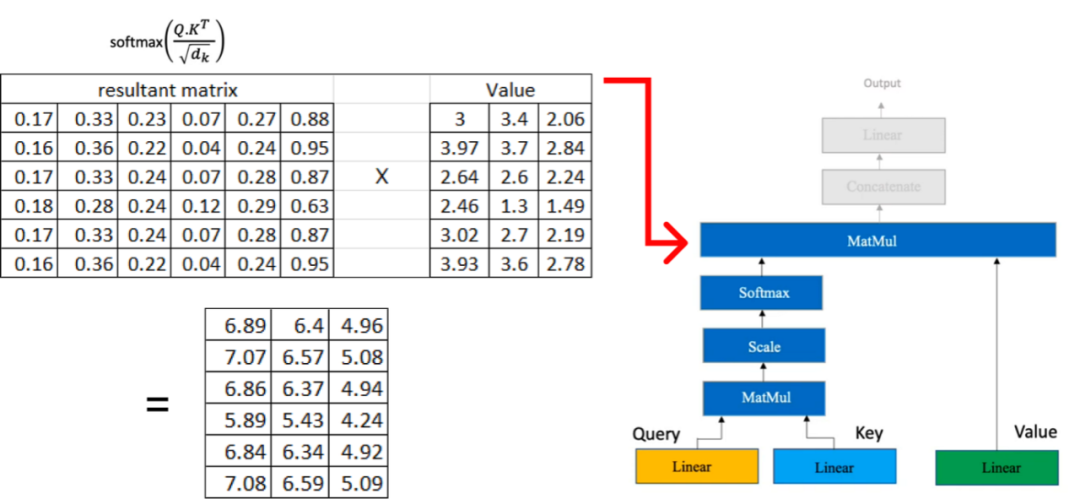
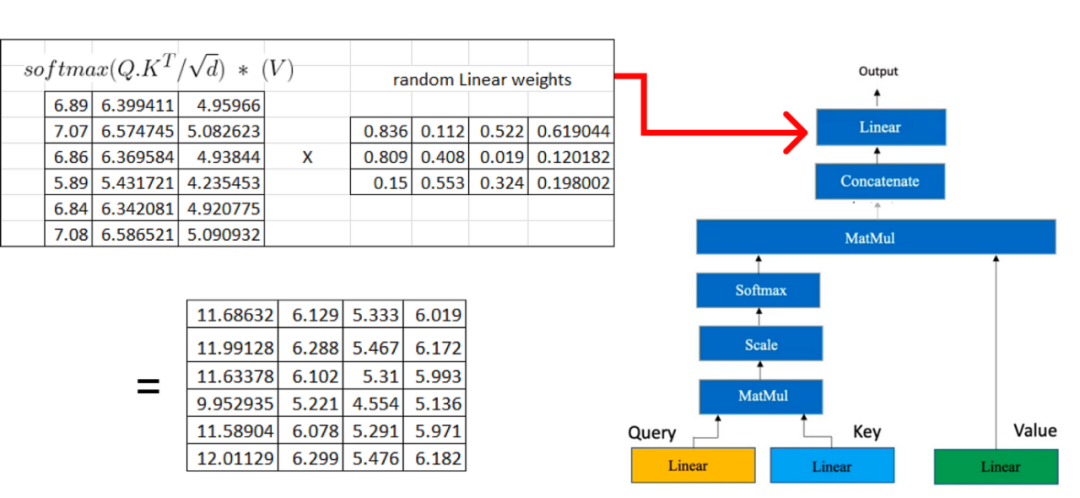
 Now, we will multiply the result matrix with the value matrix we computed earlier:
Now, we will multiply the result matrix with the value matrix we computed earlier: