
New Intelligence Report
New Intelligence Report
Source: deeplearning.ai
Editor: Daming
【New Intelligence Guide】The initialization of neural networks is a crucial step in the training process, significantly affecting the model’s performance, convergence, and convergence speed. This article is a technical blog from deeplearning.ai, which points out that improper selection of initialization values can lead to problems such as gradient explosion or gradient vanishing, and proposes targeted solutions.
Initialization has a significant impact on the training time and convergence of deep neural network models. Simple initialization methods can accelerate training, but caution is needed to avoid common pitfalls. This article will explain how to effectively initialize the parameters of a neural network.
To build a machine learning algorithm, one typically defines an architecture (e.g., logistic regression, support vector machine, neural network) and trains it to learn parameters. Here are some common steps for training a neural network:
Initialize parameters
Select optimization algorithm
Then repeat the following steps:
1. Forward propagate inputs
2. Compute cost function
3. Use backpropagation to compute cost gradients with respect to parameters
4. Update each parameter based on the optimization algorithm using gradients
Then, given a new data point, use the model to predict its type.
The initialization step is critical for the model’s final performance and requires the correct method. For instance, consider the three-layer neural network below. Different methods can be tried to initialize this network and observe their impact on learning.

In each iteration of the optimization loop (forward, cost, backward, update), we observe that as we move from the output layer to the input layer, the gradients from backpropagation are either amplified or minimized.
Assuming all activation functions are linear (identity function), the output activation is:
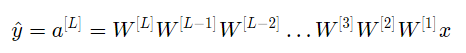
Where L=10, and W[1], W[2]…W[L-1] are 2*2 matrices, as there are 2 neurons receiving 2 inputs from the 1st layer to the L-1 layer. For ease of analysis, if we assume W[1]=W[2]=…=W[L-1]=W, then the output prediction is
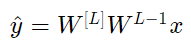
What happens if the initialization value is too large or too small?
Case 1: Too large initialization values lead to gradient explosion
If the initialization values for each weight are slightly larger than the identity matrix, i.e.,
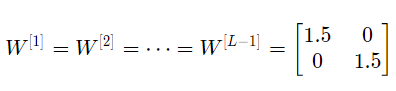
It can be simplified as
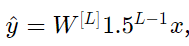
And the value of a[l] grows exponentially with l. When these activations are used for backpropagation, it leads to gradient explosion. That is, the cost gradients associated with the parameters are too large. This causes the cost to oscillate around its minimum.
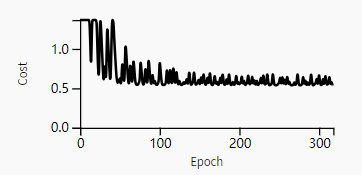
Initialization values that are too large cause the cost to oscillate around its minimum.
Case 2: Too small initialization values lead to gradient vanishing
Similarly, if the initialization values for each weight are slightly smaller than the identity matrix, i.e.,
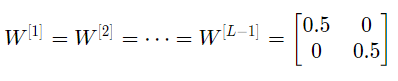
It can be simplified as
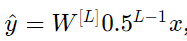
And the value of a[l] decreases exponentially with l. When these activations are used for backpropagation, it may lead to gradient vanishing. That is, the cost gradients associated with the parameters are too small. This results in the cost converging before reaching its minimum.
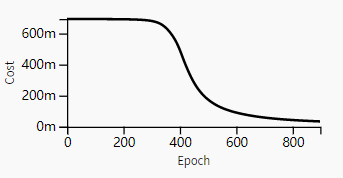
Initialization values that are too small lead to premature convergence of the model.
In summary, using inappropriate values for weights will lead to divergence of the neural network or slow down the training speed. Although we used simple symmetric weight matrices to illustrate the gradient explosion/vanishing problem, this phenomenon can be generalized to any inappropriate initialization values.
To prevent the above problems, we can adhere to the following empirical principles:
1. The mean of activations should be zero.
2. The variance of activations should remain unchanged at each layer.
Under these two assumptions, the gradient signals in backpropagation should not be multiplied by values that are too small or too large at any layer. The gradients should be able to move to the input layer without exploding or vanishing.
More specifically, for layer l, its forward propagation is:
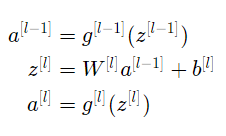
We want the following to hold:
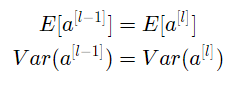
Ensuring the mean is zero and maintaining the variance of each layer’s input can guarantee that the signal does not explode or vanish. This method applies to both forward propagation (for activations) and backward propagation (for gradients of the cost with respect to activations). Here, it is recommended to use Xavier initialization (or its derived initialization methods), where for each layer l, we have:
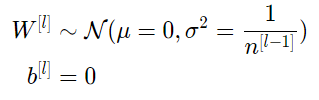
All weights in layer l are randomly selected from a normal distribution, with mean μ=0 and variance E= 1/( n[l−1]), where n[l−1] is the number of neurons in the (l-1)th layer of the network. Biases are initialized to zero.
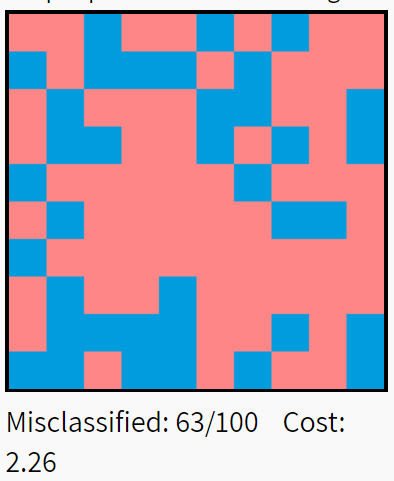
The following figure illustrates the impact of Xavier initialization on a five-layer fully connected neural network. The dataset consists of 10,000 handwritten digits selected from MNIST, with red boxes indicating misclassifications and blue indicating correct classifications.

The results show that Xavier initialization significantly outperforms uniform and standard normal distributions (from top to bottom: uniform, standard normal distribution, Xavier).


Conclusion
In practice, machine learning engineers using Xavier initialization will initialize weights as N(0,1/( n[l−1])) or N(0,2/(n[l-1]+n[1])), where the variance of the latter distribution is the harmonic mean of n[l-1] and n[1].
Xavier initialization can be used with tanh activation. Additionally, there are many other initialization methods. For instance, when using ReLU, the usual initialization is He initialization, where the initialized weights are multiplied by 2 times the variance of Xavier initialization. Although this initialization proves to be slightly more complex, the idea is the same as that of tanh.
Reference link:
https://www.deeplearning.ai/ai-notes/initialization/
New Intelligence Spring Recruitment is Open, Join Us at the Peak of AI!
For job details, click here:

[Join the Community]
New Intelligence AI Technology + Industry Community is recruiting. Students interested in AI technology + industry implementation are welcome to add the assistant’s WeChat number:aiera2015_2 to join the group; after passing the review, we will invite you to join. Please ensure to modify the group note (Name – Company – Position); the professional group review is strict, please understand.
