Convolutional Neural Networks are a type of feedforward neural network that includes convolutional operations and has a deep structure, representing one of the key algorithms in deep learning. This article aims to introduce the basic concepts and structures of CNN, as well as the fundamental ideas behind CNN architecture design.
This article is packed with valuable information and is worth saving! At the end, there is a link to GNN resources for easy access and study.
【1】Introduction
Without further ado, let’s begin.
When presented with an image, the simplest question is: what is this image?
For example, I am going to train the simplest CNN to recognize whether the letter in the image is an X or an O.

To the human eye, it’s obvious that it’s an X, but the computer doesn’t understand what X is. So we label this image, commonly known as a label, with Label=X, informing the computer that this image represents X. It then memorizes the appearance of X.
However, not all Xs look the same. For example…

These four are all Xs, but they clearly look different from the previous X, and the computer has never seen them before, so it doesn’t recognize them.
(Here we can introduce the term “underfitting” in machine learning.)
If it doesn’t recognize them, what can we do? We can recall if it has seen something similar. At this point, what CNN needs to do is to extract the features of images that represent X.
As we know, images are stored in the computer as pixel values, meaning that to the computer, two Xs actually look like this.


Here, 1 represents white, and -1 represents black.
If we compare each pixel one by one, it is certainly not scientific, leading to incorrect results and low efficiency. Therefore, alternative matching methods were proposed.
We call this patch matching.
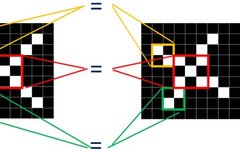
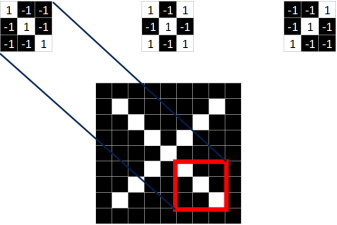
By observing these two X images, we can see that although pixel values do not correspond one-to-one, there are still some common features.
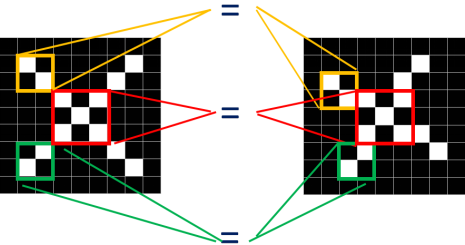
As shown in the figure, the structure of the three same-colored areas in both images is completely identical!
Therefore, we consider whether we can relate these two images. We cannot correspond all pixels, but can we match locally?
The answer is definitely yes.
For instance, if I want to locate a face in a photo, but CNN doesn’t know what a face is, I tell it: a face has three features: how the eyes, nose, and mouth look. Then I show it what these three look like. As long as CNN searches the entire image and finds the locations of these three features, it can locate the face.
Similarly, we extract three features from the standard X image.
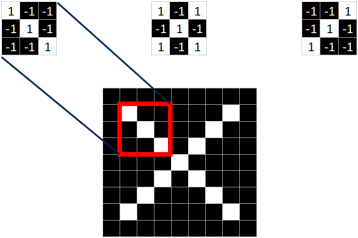
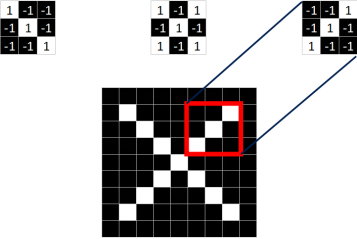
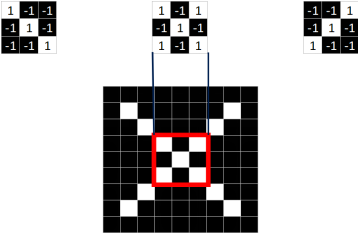
We find that we can locate a certain part of X using just these three features.
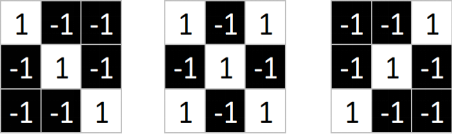
Features in CNN are also known as convolution kernels (filters), typically sized 3×3 or 5×5.
【2】Convolution Operation
After so much discussion, we finally get to the term convolution!
But!! Friends! The convolution in CNN has nothing to do with the convolution operation in signal processing! I even specifically reviewed the convolution operation from calculus! Ugh!

These!! Are unrelated to our CNN!!!
Alright, let’s continue with the calculations. Four words: multiply and correspond. Look at the diagram.
Take the (1,1) element value from the feature and the (1,1) element value from the blue box in the image, multiply them, resulting in 1. Fill this result of 1 into the new image.

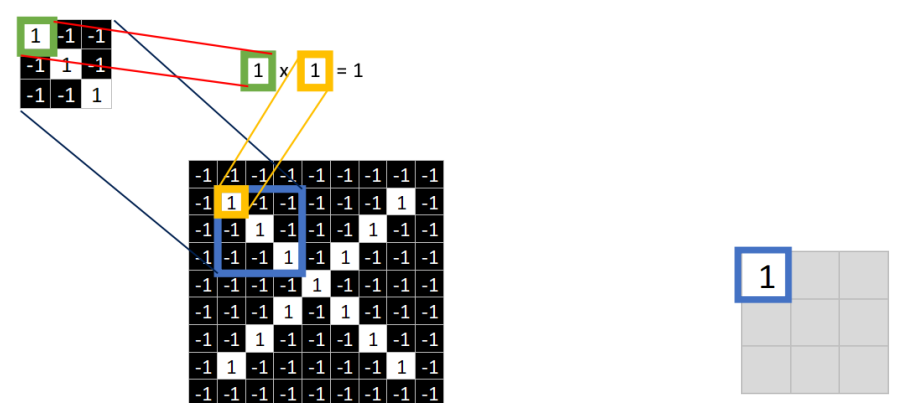
Similarly, continue calculating the values at the other eight coordinates
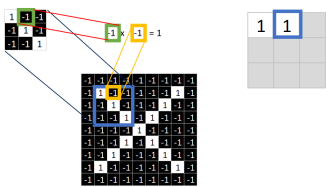
After calculating all nine, it will look like this.

The next step is to average the nine values on the right, obtaining a mean value, which is then filled into a new image.
This new image is called the feature map.

Some little friends may want to raise their hands and ask why the blue box is placed in this position in the image?
This is just an example. This blue box is called a “window,” and its property is that it can slide.
Initially, it should be at the starting position.

After performing the convolution corresponding multiplication operation and calculating the mean, the sliding window begins to move to the right. The sliding distance depends on the chosen stride.
For example, if the stride = 1, it moves one pixel to the right.

If the stride = 2, it moves two pixels to the right.
After moving to the far right, it returns to the left and starts the second row. Similarly, if the stride = 1, it moves down one pixel; if the stride = 2, it moves down two pixels.
Finally, after a series of convolutions and averaging operations, we fill a complete feature map.
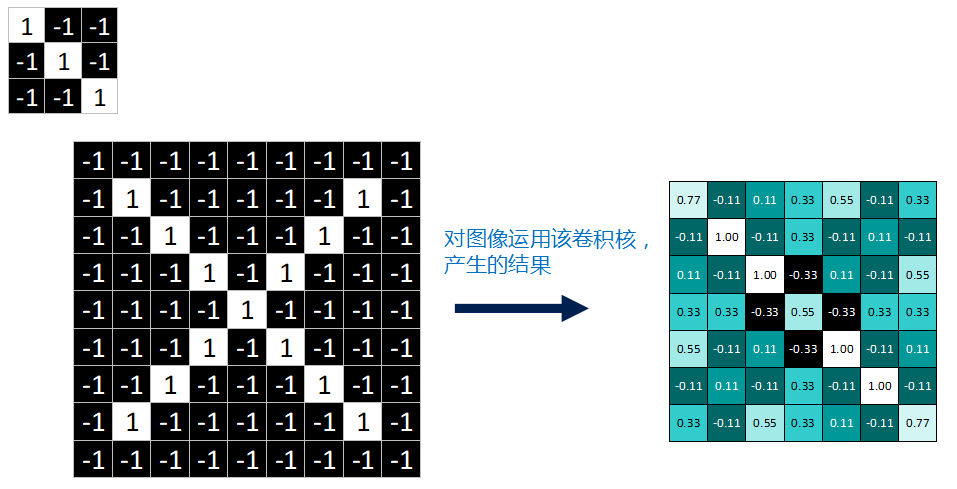
The feature map is the “features” extracted from the original image for each feature. The values within it, the closer they are to 1, indicate a more complete match at that position with the feature, while values closer to -1 indicate a more complete opposite match, and values close to 0 indicate no match or correlation.
One feature produces one feature map for the image, and for this X image, we use three features, thus producing three feature maps in total.

Thus, the section on convolution operations is complete!
Recently, I have also compiled a collection of GNN resources, which includes videos, books, papers, and projects. Interested students can click on my business card to get it.
【3】Non-linear Activation Layer
The convolution layer performs multiple convolutions on the original image, producing a set of linear activation responses, while the non-linear activation layer applies a non-linear activation response to the previous results.
This is a very formal statement, and I wonder if everyone feels confused reading it.
Well~ it’s really not that complicated!
This series of articles adheres to the principle of “speaking in plain language!” and aims to explain those incomprehensible concepts in books using the simplest and most accessible language.
The most commonly used non-linear activation function in neural networks is the ReLU function, defined as follows:
f(x) = max(0, x)
That is, it retains values greater than or equal to 0, while all values less than 0 are directly rewritten as 0.
Why do we do this? As mentioned earlier, the values in the feature map produced after convolution, the closer they are to 1, indicate a stronger association with that feature, while values closer to -1 indicate a weaker association. To make the data less and operations easier during feature extraction, we directly discard those unrelated data.
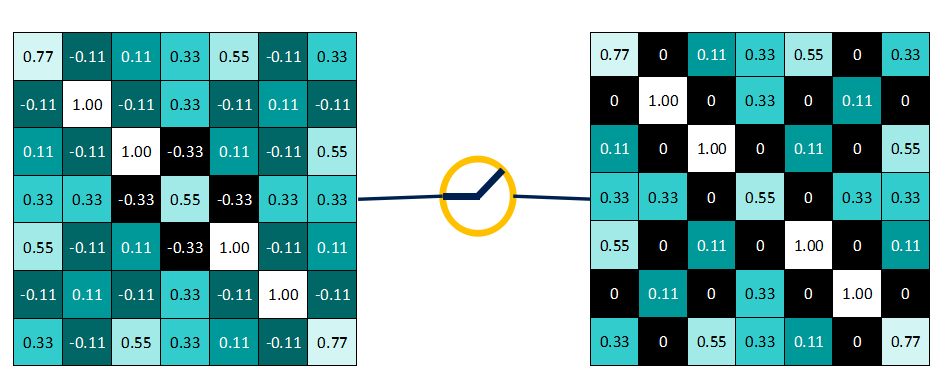
As shown in the figure: values >= 0 remain unchanged.

And values < 0 are all rewritten as 0.
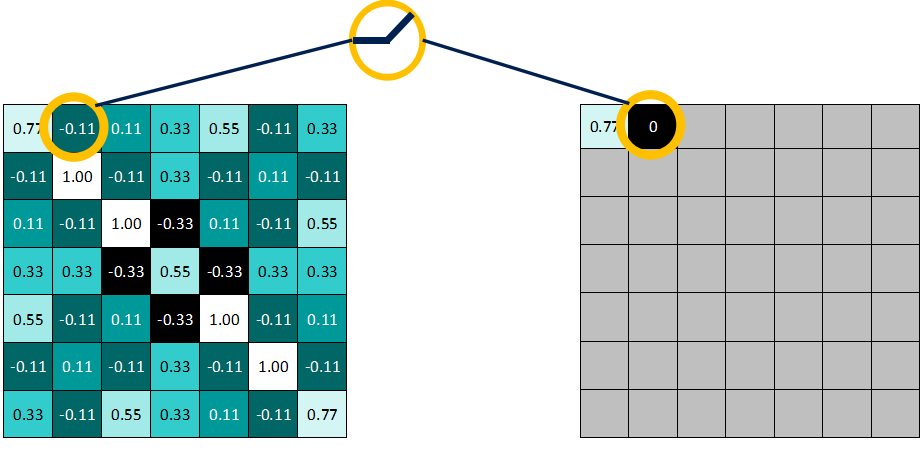
Result after applying the non-linear activation function:
【4】Pooling Layer
After the convolution operation, we obtain various feature maps with different values. Although the data volume is much smaller than the original image, it is still too large (considering that deep learning often involves hundreds of thousands of training images). Therefore, the subsequent pooling operation can play its role, with the primary goal of reducing data volume.
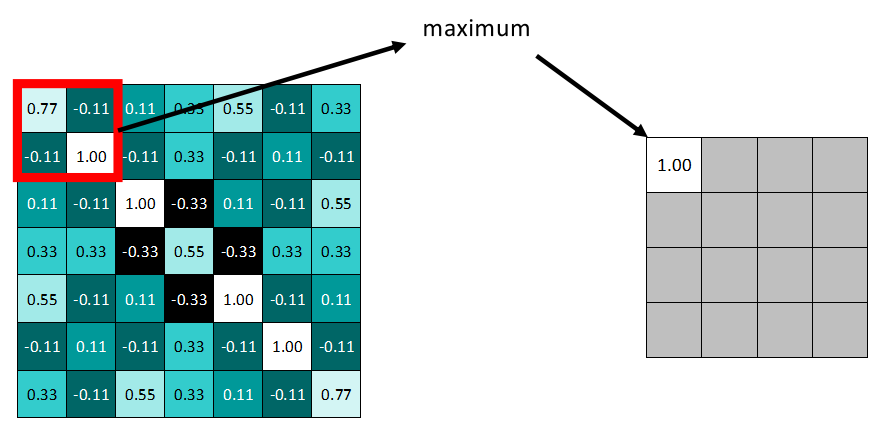
Pooling is divided into two types: Max Pooling and Average Pooling. As the names suggest, Max Pooling takes the maximum value, while Average Pooling takes the average value.
Taking Max Pooling as an example: selecting a pooling size of 2×2, we choose the maximum value within that 2×2 window to update into the new feature map.
Similarly, slide the window to the right based on the stride.
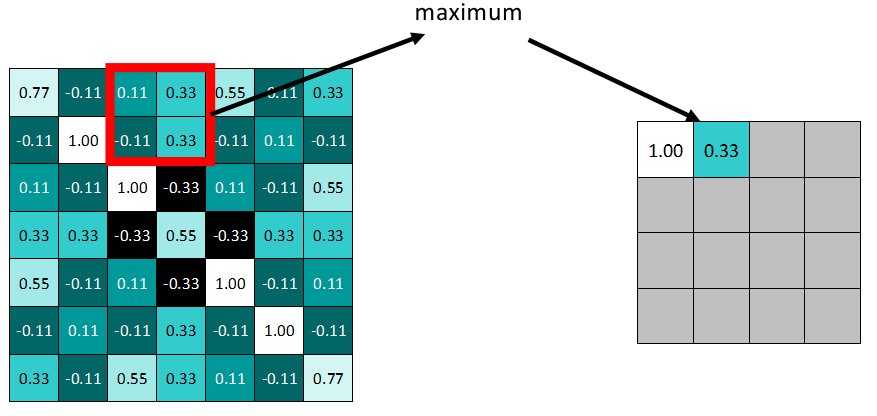

Ultimately, we get the pooled feature map. It is evident that the data volume has significantly reduced.
Since Max Pooling retains the maximum value from each small block, it effectively preserves the best matching result within that block (because values closer to 1 indicate better matching). This means it does not specifically focus on which exact location within the window matched, but rather whether some location matched. This demonstrates that CNN can identify whether an image contains a certain feature without caring where that feature is located. This helps resolve the rigid approach of matching each pixel individually.
At this point, we have introduced the basic configuration of CNN—the convolution layer, the ReLU layer, and the pooling layer.
In several common CNN architectures, these three layers can be stacked, using the output of the previous layer as the input for the next. For example:
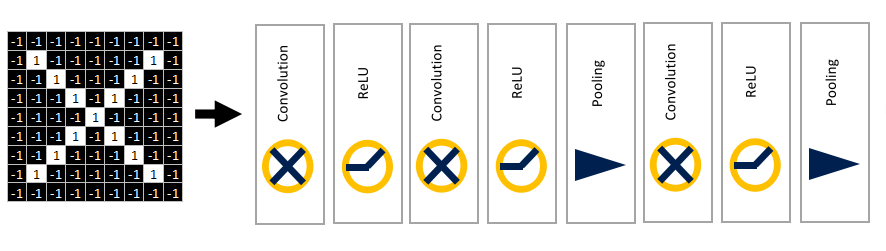
More layers can also be added to create more complex neural networks.
Finally, there are fully connected layers and the training and optimization of the neural network.
Recently, I also compiled a collection of GNN resources, including videos, books, papers, and projects. Interested students can click on my business card to get it.