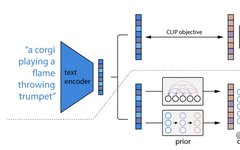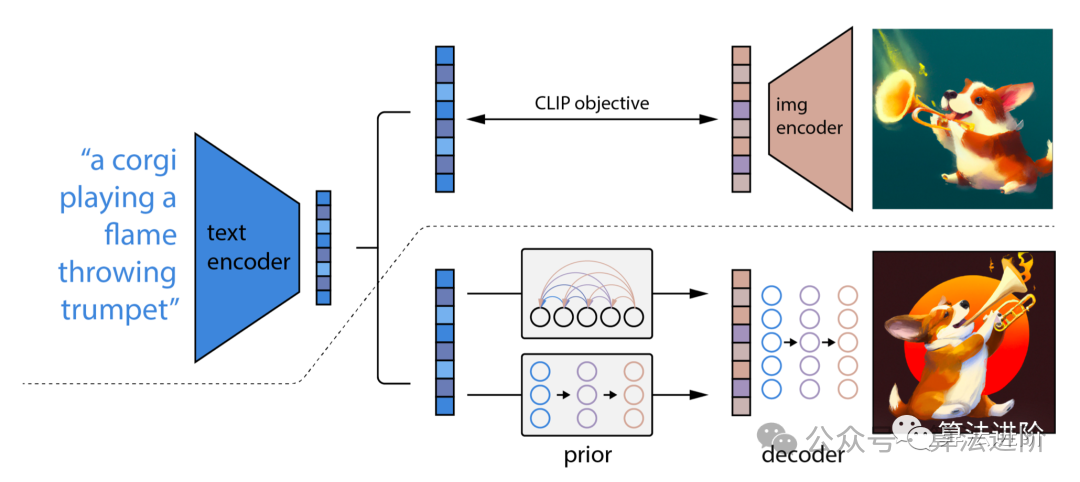
The catalyst for diffusion models began with the introduction of DDPM (Denoising Diffusion Probabilistic Model) in 2020. Before delving into the details of how the denoising diffusion probabilistic model (DDPM) works, let’s first look at some developments in existing generative artificial intelligence, which are foundational studies for DDPM:
VAE
VAEs utilize an encoder, probabilistic latent space, and decoder. During training, the encoder predicts the mean and variance for each image. These values are then sampled from a Gaussian distribution and passed to the decoder, where the input image is expected to resemble the output image. This process includes using KL Divergence to compute the loss. A significant advantage of VAEs is their ability to generate a wide variety of images. In the sampling phase, simply sampling from the Gaussian distribution allows the decoder to create a new image.
GAN
Just a year after the introduction of variational autoencoders (VAEs), a groundbreaking generative family model emerged—Generative Adversarial Networks (GANs), marking the beginning of a new class of generative models characterized by the collaboration of two neural networks: a generator and a discriminator, involving an adversarial training process. The generator’s goal is to produce realistic data, such as images, from random noise, while the discriminator works to distinguish real data from generated data. Throughout the training phase, the generator and discriminator continuously refine their abilities through a competitive learning process. The generator creates increasingly convincing data, becoming smarter than the discriminator, while the discriminator enhances its ability to differentiate between real and generated samples. This adversarial interaction peaks when the generator produces high-quality, realistic data. In the sampling phase, after GAN training, the generator produces new samples from input random noise, transforming this noise into data that typically reflects real examples.
Why Do We Need Diffusion Models: DDPM
Both models have different issues; while GANs excel at generating realistic images that closely resemble those in the training set, VAEs are good at creating a variety of images, albeit with a tendency to produce blurry images. However, existing models have not successfully combined these two functionalities—creating images that are both highly realistic and diverse. This challenge presents a significant barrier for researchers to overcome.
Six years after the first GAN paper was published and seven years after the VAE paper was released, a groundbreaking model emerged: the Denoising Diffusion Probabilistic Model (DDPM). DDPM combines the advantages of both models, excelling at creating diverse and realistic images.

In this article, we will delve into the complexities of DDPM, covering its training process, including the forward and reverse processes, and exploring how to perform sampling. Throughout this exploration, we will use PyTorch to build DDPM from scratch and complete its full training.
It is assumed that you are already familiar with the basics of deep learning and have a solid foundation in deep computer vision. We will not introduce these basic concepts; our goal is to generate images that humans are convinced of their authenticity.
Diffusion Model DDPM
The Denoising Diffusion Probabilistic Model (DDPM) is a cutting-edge method in the field of generative models. Unlike traditional models that rely on explicit likelihood functions, DDPM operates by iteratively denoising through a diffusion process. This involves gradually adding noise to an image and attempting to remove that noise. Its fundamental theory is based on the idea that by transforming a simple distribution, such as a Gaussian distribution, through a series of diffusion steps, one can obtain a complex and expressive image data distribution. In other words, by transferring samples from the original image distribution to a Gaussian distribution, we can create a model to reverse this process. This allows us to start from a fully Gaussian distribution and end with an image distribution, effectively generating new images.
The training of DDPM includes two basic steps: generating noisy images, which is a fixed and non-learnable forward process, followed by the reverse process. The main goal of the reverse process is to denoise the image using a specialized machine learning model.
Forward Diffusion Process
The forward process is a fixed and non-learnable step, but it requires some predefined settings. Before delving into these settings, let’s first understand how it works.
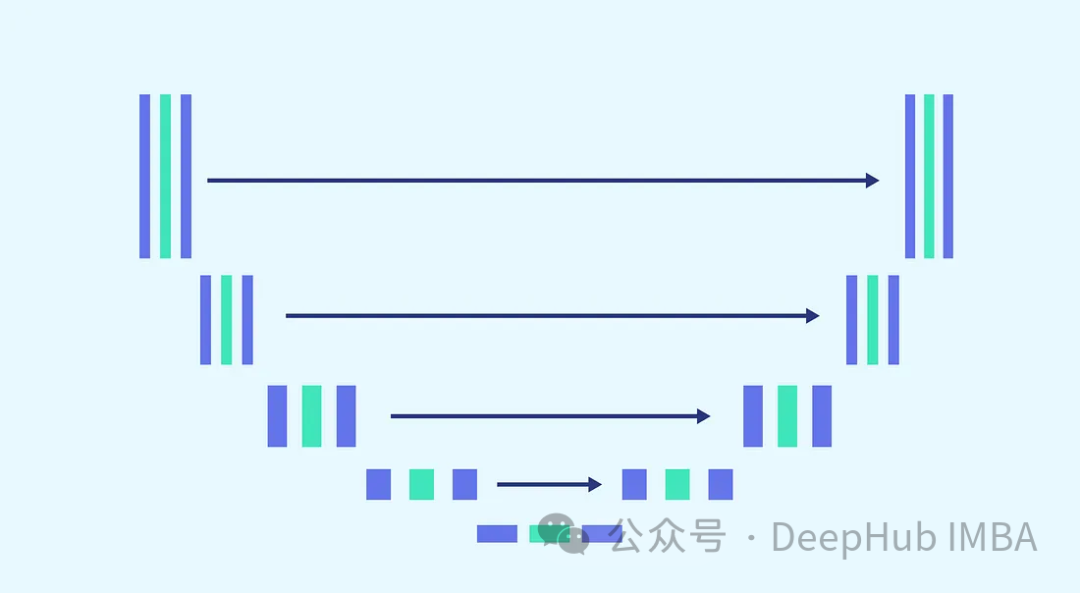
The core concept of this process is to start with a clear image. At a specific step denoted by “T”, a small amount of noise is gradually introduced according to a Gaussian distribution.

As can be seen from the image, the noise is incrementally added at each step, and we will delve into the mathematical representation of this noise.
The noise is sampled from a Gaussian distribution. To introduce a small amount of noise at each step, we use a Markov chain. To generate the image at the current timestamp, we only need the image from the previous timestamp. The concept of the Markov chain is key here and is crucial for the subsequent mathematical details.
A Markov chain is a stochastic process where the probability of transitioning to any specific state depends only on the current state and the elapsed time, rather than the sequence of events that preceded it. This property simplifies the modeling of the noise addition process, making it easier for mathematical analysis.
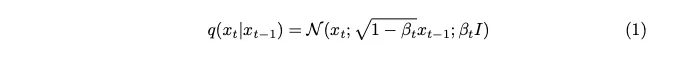
The variance parameter denoted by beta is deliberately set to a very small value, with the aim of introducing only a minimal amount of noise at each step.
The step parameter “T” determines the number of steps required to generate a fully noisy image. In this article, this parameter is set to 1000, which may seem large. Do we really need to create 1000 noisy images for each original image in the dataset? The aspect of the Markov chain proves helpful in addressing this issue. Since we only need the previous image to predict the next one, and the noise added at each step remains constant, we can simplify the computation by generating the noisy image for a specific timestamp. The right reparameterization technique allows us to further simplify the equations.

By incorporating the new parameters introduced in equation (3) into equation (2), we have developed equation (2) to obtain the result.
Reverse Diffusion Process
Now that we have introduced noise into the image, the next step is to perform the reverse operation. Mathematically, it is impossible to denoise the image unless we know the initial conditions, namely the denoised image at t = 0. Our goal is to sample directly from noise to create new images, where the lack of information about the outcome poses a challenge. Therefore, I need to design a method to progressively denoise the image without knowing the result. This leads to the solution of using a deep learning model to approximate this complex mathematical function.
With a bit of mathematical background, the model will approximate equation (5). A notable detail is that we will adhere to the original DDPM paper and maintain a fixed variance, although it is also possible to allow the model to learn it.

The task of the model is to predict the average noise added between the current timestamp and the previous timestamp. By doing so, we can effectively remove noise and achieve the desired effect. But what if our goal is to have the model predict the noise added from the “original image” to the last timestamp?
Mathematically, performing the reverse process is challenging unless we know the initial image without noise, so let’s start by defining the posterior variance.

The task of the model is to predict the noise of the image added at timestamp t from the initial image. The forward process allows us to perform this operation, starting from a clear image and progressing to a noisy image at timestamp t.
Training Algorithm
We assume that the architecture of the model used for prediction will be a U-Net. The goal during the training phase is: for each image in the dataset, randomly select a timestamp within the range [0, T] and compute the forward diffusion process. This produces a clear, slightly noisy image, along with the actual noise used. Then, using our understanding of the reverse process, we utilize the model to predict the noise added to the image. With the real and predicted noise, we seem to have entered a supervised machine learning problem.
The main question arises: which loss function should we use to train our model? Given that we are dealing with a probabilistic latent space, Kullback-Leibler (KL) divergence is a suitable choice.
KL divergence measures the difference between two probability distributions, in our case, the distribution predicted by the model and the expected distribution. Including KL divergence in the loss function not only guides the model to produce accurate predictions but also ensures that the latent space representation conforms to the desired probabilistic structure.
KL divergence can be approximated as an L2 loss function, so we can derive the following loss function:

Ultimately, we arrive at the training algorithm proposed in the paper.

Sampling
The reverse process has been explained, and now we will discuss how to use it. Starting from a completely random image at timestamp T and using the reverse process T times, we ultimately arrive at timestamp 0. This constitutes the second algorithm outlined in this article.

Parameters
We have many different parameters such as beta, beta_tildes, alpha, alpha_hat, etc. Currently, it is not known how to select these parameters. However, the only known parameter at this time is T, which is set to 1000.
For all the listed parameters, their selection depends on beta. In a sense, beta determines the amount of noise we want to add at each step. Therefore, careful selection of beta is crucial for the success of the algorithm. As for the other parameters, please refer to the paper as there are too many.
Various sampling methods were explored during the experimental phase of the original paper. The initial linear sampling method resulted in images that were either under-noised or became overly noisy. To address this issue, another more commonly used method, cosine sampling, was adopted. Cosine sampling provides smoother and more consistent noise addition.
Implementing Diffusion Models in PyTorch
We will utilize the U-Net architecture for noise prediction; the reason for choosing U-Net is that it is an ideal architecture for image processing, capturing spatial and feature maps, and providing output sizes that match the input.
Considering the complexity of the task and the requirement to use the same model for each step (where the model needs to denoise both completely noisy images and slightly noisy images with the same weights), adjusting the model is essential. This includes merging more complex blocks and introducing temporal awareness through sinusoidal embedding steps. The purpose of these enhancements is to make the model an expert in the denoising task. Before proceeding to build the complete model, we will introduce each block.
ConvNext Block
To meet the need for increased model complexity, convolutional blocks play a crucial role. Here, we cannot solely rely on the basic blocks from the U-Net paper; we will incorporate ConvNext.
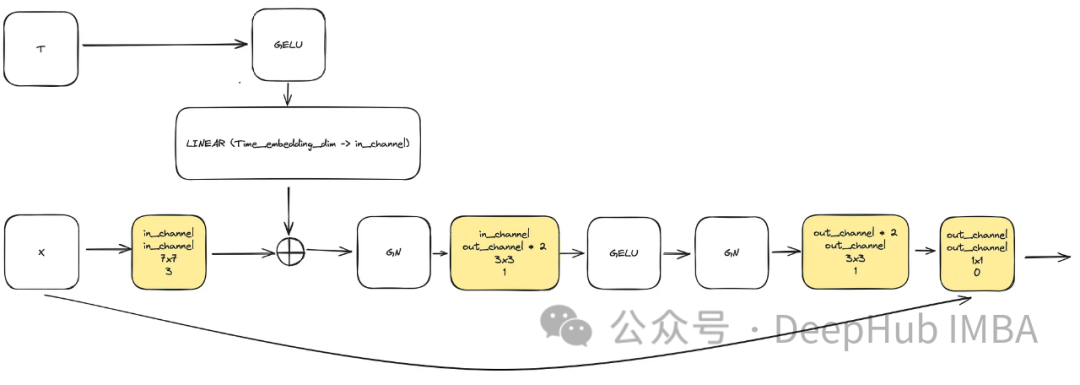
The input consists of the image represented by “x” and the timestamp visualization of size “time_embedding_dim” denoted by “t”. Due to the complexity of the blocks and the residual connections with the input and final layer, the blocks play a key role in learning spatial and feature mapping throughout the process.
class ConvNextBlock(nn.Module):
def __init__(self,
in_channels,
out_channels,
mult=2,
time_embedding_dim=None,
norm=True,
group=8,
):
super().__init__()
self.mlp = (
nn.Sequential(nn.GELU(), nn.Linear(time_embedding_dim, in_channels))
if time_embedding_dim
else None
)
self.in_conv = nn.Conv2d(
in_channels, in_channels, 7, padding=3, groups=in_channels
)
self.block = nn.Sequential(
nn.GroupNorm(1, in_channels) if norm else nn.Identity(),
nn.Conv2d(in_channels, out_channels * mult, 3, padding=1),
nn.GELU(),
nn.GroupNorm(1, out_channels * mult),
nn.Conv2d(out_channels * mult, out_channels, 3, padding=1),
)
self.residual_conv = (
nn.Conv2d(in_channels, out_channels, 1)
if in_channels != out_channels
else nn.Identity()
)
def forward(self, x, time_embedding=None):
h = self.in_conv(x)
if self.mlp is not None and time_embedding is not None:
assert self.mlp is not None, "MLP is None"
h = h + rearrange(self.mlp(time_embedding), "b c -> b c 1 1")
h = self.block(h)
return h + self.residual_conv(x)Sinusoidal Timestamp Embedding
One of the key blocks in the model is the sinusoidal timestamp embedding block, which allows the encoding of the given timestamp to retain information about the current time needed for the model’s decoding, as the model will be used for all different timestamps.
This is a very classic implementation and is applied everywhere, so we will directly paste the code here.
class SinusoidalPosEmb(nn.Module):
def __init__(self, dim, theta=10000):
super().__init__()
self.dim = dim
self.theta = theta
def forward(self, x):
device = x.device
half_dim = self.dim // 2
emb = math.log(self.theta) / (half_dim - 1)
emb = torch.exp(torch.arange(half_dim, device=device) * -emb)
emb = x[:, None] * emb[None, :]
emb = torch.cat((emb.sin(), emb.cos()), dim=-1)
return embDownSample & UpSample
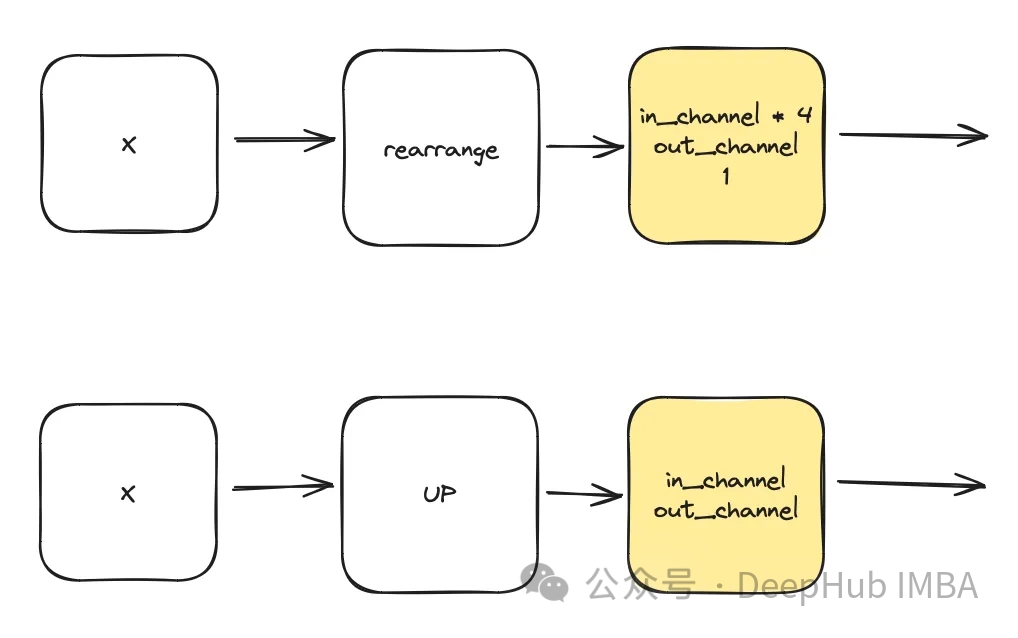
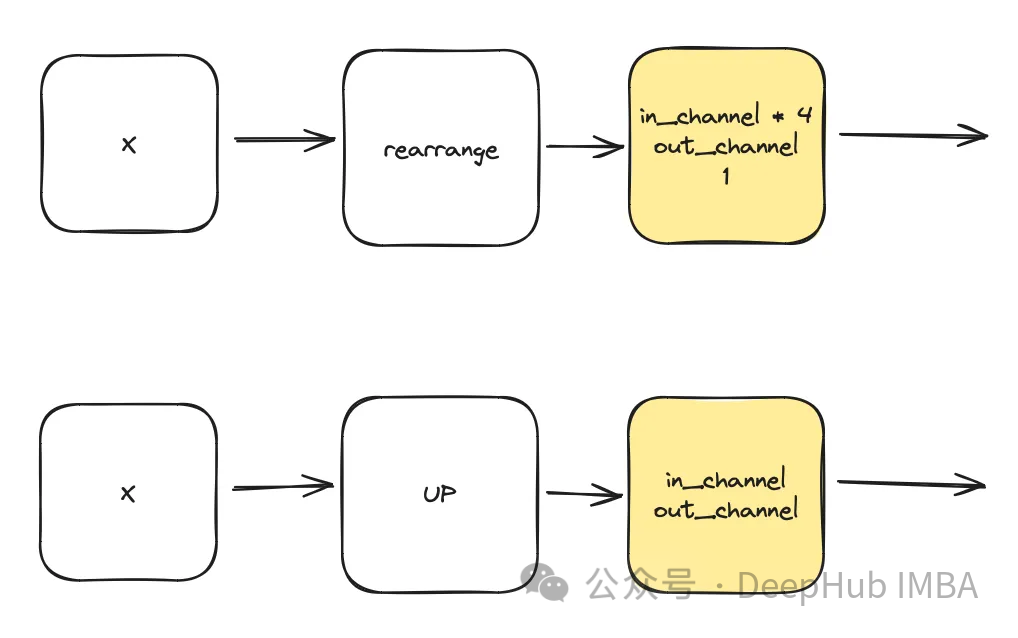
class DownSample(nn.Module):
def __init__(self, dim, dim_out=None):
super().__init__()
self.net = nn.Sequential(
Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),
nn.Conv2d(dim * 4, default(dim_out, dim), 1),
)
def forward(self, x):
return self.net(x)
class Upsample(nn.Module):
def __init__(self, dim, dim_out=None):
super().__init__()
self.net = nn.Sequential(
nn.Upsample(scale_factor=2, mode="nearest"),
nn.Conv2d(dim, dim_out or dim, kernel_size=3, padding=1),
)
def forward(self, x):
return self.net(x)Time Multi-Layer Perceptron
This module utilizes it to create time representations based on the given timestamp t. The output of this multi-layer perceptron (MLP) will also serve as input “t” for all modified ConvNext blocks.

Here, “dim” is a hyperparameter of the model representing the number of channels required for the first block. It serves as the basic calculation for the number of channels in subsequent blocks.
sinu_pos_emb = SinusoidalPosEmb(dim, theta=10000)
time_dim = dim * 4
time_mlp = nn.Sequential(
sinu_pos_emb,
nn.Linear(dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim),
)Attention
This is an optional component used in the U-Net. Attention helps enhance the role of residual connections in learning. It focuses more on important spatial information obtained from the left side of the Unet through a residual connection calculated with an attention mechanism and feature mapping in the mid-low latent space. It originates from the ACC-UNet paper.
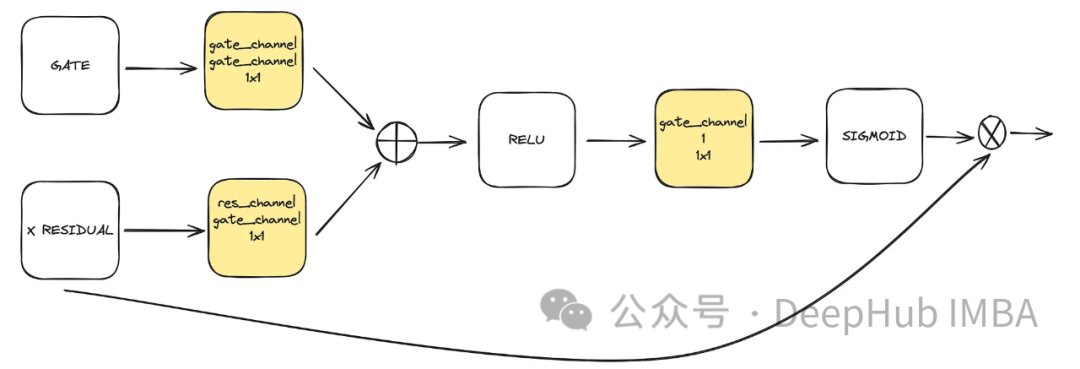
The gate represents the upsampling output of the lower block, while the residual x indicates the residual connection at the level where attention is applied.
class BlockAttention(nn.Module):
def __init__(self, gate_in_channel, residual_in_channel, scale_factor):
super().__init__()
self.gate_conv = nn.Conv2d(gate_in_channel, gate_in_channel, kernel_size=1, stride=1)
self.residual_conv = nn.Conv2d(residual_in_channel, gate_in_channel, kernel_size=1, stride=1)
self.in_conv = nn.Conv2d(gate_in_channel, 1, kernel_size=1, stride=1)
self.relu = nn.ReLU()
self.sigmoid = nn.Sigmoid()
def forward(self, x: torch.Tensor, g: torch.Tensor) -> torch.Tensor:
in_attention = self.relu(self.gate_conv(g) + self.residual_conv(x))
in_attention = self.in_conv(in_attention)
in_attention = self.sigmoid(in_attention)
return in_attention * xFinal Integration
Integrate all the blocks discussed earlier (excluding the attention block) into a U-Net. Each block contains two residual connections instead of one. This modification is to address potential overfitting issues.

class TwoResUNet(nn.Module):
def __init__(self,
dim,
init_dim=None,
out_dim=None,
dim_mults=(1, 2, 4, 8),
channels=3,
sinusoidal_pos_emb_theta=10000,
convnext_block_groups=8,
):
super().__init__()
self.channels = channels
input_channels = channels
self.init_dim = default(init_dim, dim)
self.init_conv = nn.Conv2d(input_channels, self.init_dim, 7, padding=3)
dims = [self.init_dim, *map(lambda m: dim * m, dim_mults)]
in_out = list(zip(dims[:-1], dims[1:]))
sinu_pos_emb = SinusoidalPosEmb(dim, theta=sinusoidal_pos_emb_theta)
time_dim = dim * 4
self.time_mlp = nn.Sequential(
sinu_pos_emb,
nn.Linear(dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim),
)
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out)
for ind, (dim_in, dim_out) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1)
self.downs.append(
nn.ModuleList(
[
ConvNextBlock(
in_channels=dim_in,
out_channels=dim_in,
time_embedding_dim=time_dim,
group=convnext_block_groups,
),
ConvNextBlock(
in_channels=dim_in,
out_channels=dim_in,
time_embedding_dim=time_dim,
group=convnext_block_groups,
),
DownSample(dim_in, dim_out)
if not is_last
else nn.Conv2d(dim_in, dim_out, 3, padding=1),
]
)
)
mid_dim = dims[-1]
self.mid_block1 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)
self.mid_block2 = ConvNextBlock(mid_dim, mid_dim, time_embedding_dim=time_dim)
for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):
is_last = ind == (len(in_out) - 1)
is_first = ind == 0
self.ups.append(
nn.ModuleList(
[
ConvNextBlock(
in_channels=dim_out + dim_in,
out_channels=dim_out,
time_embedding_dim=time_dim,
group=convnext_block_groups,
),
ConvNextBlock(
in_channels=dim_out + dim_in,
out_channels=dim_out,
time_embedding_dim=time_dim,
group=convnext_block_groups,
),
Upsample(dim_out, dim_in)
if not is_last
else nn.Conv2d(dim_out, dim_in, 3, padding=1)
]
)
)
default_out_dim = channels
self.out_dim = default(out_dim, default_out_dim)
self.final_res_block = ConvNextBlock(dim * 2, dim, time_embedding_dim=time_dim)
self.final_conv = nn.Conv2d(dim, self.out_dim, 1)
def forward(self, x, time):
b, _, h, w = x.shape
x = self.init_conv(x)
r = x.clone()
t = self.time_mlp(time)
unet_stack = []
for down1, down2, downsample in self.downs:
x = down1(x, t)
unet_stack.append(x)
x = down2(x, t)
unet_stack.append(x)
x = downsample(x)
x = self.mid_block1(x, t)
x = self.mid_block2(x, t)
for up1, up2, upsample in self.ups:
x = torch.cat((x, unet_stack.pop()), dim=1)
x = up1(x, t)
x = torch.cat((x, unet_stack.pop()), dim=1)
x = up2(x, t)
x = upsample(x)
x = torch.cat((x, r), dim=1)
x = self.final_res_block(x, t)
return self.final_conv(x)Implementation of the Diffusion Process
Finally, we will introduce how diffusion is implemented. Since we have already covered all the mathematical theories for the forward, reverse, and sampling processes, we will focus on the code here.
class DiffusionModel(nn.Module):
SCHEDULER_MAPPING = {
"linear": linear_beta_schedule,
"cosine": cosine_beta_schedule,
"sigmoid": sigmoid_beta_schedule,
}
def __init__(self,
model: nn.Module,
image_size: int,
*,
beta_scheduler: str = "linear",
timesteps: int = 1000,
schedule_fn_kwargs: dict | None = None,
auto_normalize: bool = True,
) -> None:
super().__init__()
self.model = model
self.channels = self.model.channels
self.image_size = image_size
self.beta_scheduler_fn = self.SCHEDULER_MAPPING.get(beta_scheduler)
if self.beta_scheduler_fn is None:
raise ValueError(f"unknown beta schedule {beta_scheduler}")
if schedule_fn_kwargs is None:
schedule_fn_kwargs = {}
betas = self.beta_scheduler_fn(timesteps, **schedule_fn_kwargs)
alphas = 1.0 - betas
alphas_cumprod = torch.cumprod(alphas, dim=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
posterior_variance = (
betas * (1.0 - alphas_cumprod_prev) / (1.0 - alphas_cumprod)
)
register_buffer = lambda name, val: self.register_buffer(
name, val.to(torch.float32)
)
register_buffer("betas", betas)
register_buffer("alphas_cumprod", alphas_cumprod)
register_buffer("alphas_cumprod_prev", alphas_cumprod_prev)
register_buffer("sqrt_recip_alphas", torch.sqrt(1.0 / alphas))
register_buffer("sqrt_alphas_cumprod", torch.sqrt(alphas_cumprod))
register_buffer(
"sqrt_one_minus_alphas_cumprod", torch.sqrt(1.0 - alphas_cumprod)
)
register_buffer("posterior_variance", posterior_variance)
timesteps, *_ = betas.shape
self.num_timesteps = int(timesteps)
self.sampling_timesteps = timesteps
self.normalize = normalize_to_neg_one_to_one if auto_normalize else identity
self.unnormalize = unnormalize_to_zero_to_one if auto_normalize else identity
@torch.inference_mode()
def p_sample(self, x: torch.Tensor, timestamp: int) -> torch.Tensor:
b, *_, device = *x.shape, x.device
batched_timestamps = torch.full(
(b,), timestamp, device=device, dtype=torch.long
)
preds = self.model(x, batched_timestamps)
betas_t = extract(self.betas, batched_timestamps, x.shape)
sqrt_recip_alphas_t = extract(
self.sqrt_recip_alphas, batched_timestamps, x.shape
)
sqrt_one_minus_alphas_cumprod_t = extract(
self.sqrt_one_minus_alphas_cumprod, batched_timestamps, x.shape
)
predicted_mean = sqrt_recip_alphas_t * (
x - betas_t * preds / sqrt_one_minus_alphas_cumprod_t
)
if timestamp == 0:
return predicted_mean
else:
posterior_variance = extract(
self.posterior_variance, batched_timestamps, x.shape
)
noise = torch.randn_like(x)
return predicted_mean + torch.sqrt(posterior_variance) * noise
@torch.inference_mode()
def p_sample_loop(
self, shape: tuple, return_all_timesteps: bool = False
) -> torch.Tensor:
batch, device = shape[0], "mps"
img = torch.randn(shape, device=device)
# This cause me a RunTimeError on MPS device due to MPS back out of memory
# No ideas how to resolve it at this point
# imgs = [img]
for t in tqdm(reversed(range(0, self.num_timesteps)), total=self.num_timesteps):
img = self.p_sample(img, t)
# imgs.append(img)
ret = img # if not return_all_timesteps else torch.stack(imgs, dim=1)
ret = self.unnormalize(ret)
return ret
def sample(
self, batch_size: int = 16, return_all_timesteps: bool = False
) -> torch.Tensor:
shape = (batch_size, self.channels, self.image_size, self.image_size)
return self.p_sample_loop(shape, return_all_timesteps=return_all_timesteps)
def q_sample(
self, x_start: torch.Tensor, t: int, noise: torch.Tensor = None
) -> torch.Tensor:
if noise is None:
noise = torch.randn_like(x_start)
sqrt_alphas_cumprod_t = extract(self.sqrt_alphas_cumprod, t, x_start.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
self.sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
def p_loss(
self,
x_start: torch.Tensor,
t: int,
noise: torch.Tensor = None,
loss_type: str = "l2",
) -> torch.Tensor:
if noise is None:
noise = torch.randn_like(x_start)
x_noised = self.q_sample(x_start, t, noise=noise)
predicted_noise = self.model(x_noised, t)
if loss_type == "l2":
loss = F.mse_loss(noise, predicted_noise)
elif loss_type == "l1":
loss = F.l1_loss(noise, predicted_noise)
else:
raise ValueError(f"unknown loss type {loss_type}")
return loss
def forward(self, x: torch.Tensor) -> torch.Tensor:
b, c, h, w, device, img_size = *x.shape, x.device, self.image_size
assert h == w == img_size, f"image size must be {img_size}"
timestamp = torch.randint(0, self.num_timesteps, (1,)).long().to(device)
x = self.normalize(x)
return self.p_loss(x, timestamp)The diffusion process is part of the training model. It opens a sampling interface that allows us to generate samples using the already trained model.
Summary of Training Points
For the training part, we set up 37,000 training steps with a batch size of 16. Due to GPU memory allocation limits, the image size is restricted to 128×128. Using exponential moving average (EMA) model weights, samples were generated every 1000 steps to smooth the sampling and save model versions.
In the initial 1000 training steps, the model began to capture some features but still missed certain areas. Around 10,000 steps, this model started to produce promising results, with progress becoming more apparent. By the end of 30,000 steps, the quality of the results significantly improved, but black images were still present. This was simply because the model did not have enough sample variety, and the data distribution of real images had not been fully mapped to the Gaussian distribution.

With the final model weights, we can generate some images. Although the image quality is limited due to the 128×128 size restriction, the model’s performance is still impressive.

Note: The dataset used in this article consists of satellite images of forest terrain; please refer to the ETL section in the source code for specific acquisition methods.
Conclusion
We have comprehensively introduced the necessary knowledge about diffusion models and provided a complete implementation using PyTorch.
The code for this article:
https://github.com/Camaltra/this-is-not-real-aerial-imagery/
Related Papers:
DDPM Paper https://arxiv.org/abs/2006.11239 ConvNext Paper https://arxiv.org/abs/2201.03545 UNet Paper: https://arxiv.org/abs/1505.04597 ACC UNet: https://arxiv.org/abs/2308.13680