Summary of Hessian Matrix Application in XGBoost

Important content delivered promptly

The most common application of the Hessian matrix is in the Newton method optimization algorithm, which primarily seeks the extrema of a function where the first derivative is zero. This article provides a clear summary of two applications of the Hessian matrix in the XGBoost algorithm: the weight quantile algorithm and the sample weight sum algorithm.

1. Definition of Hessian Matrix

2. Sample Weight Sum Algorithm

3. Weight Quantile Algorithm

4. Conclusion

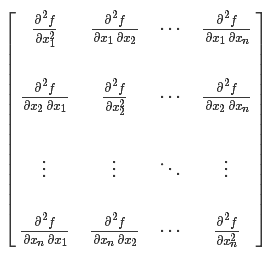
The Hessian matrix (Hessian matrix or Hessian) is a square matrix of second-order partial derivatives of a real-valued function with vector variables, defined as follows:

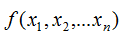
With vector variables:

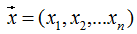
Thus, the Hessian matrix H(f) is defined as:

The official documentation defines the XGBoost algorithm parameter minimum leaf node sample weight sum (min_child_weight) as:

minimum sum of instance weight (hessian) needed in a child. If the tree partition step results in a leaf node with the sum of instance weight less than min_child_weight, then the building process will give up further partitioning. In linear regression mode, this simply corresponds to minimum number of instances needed to be in each node. The larger, the more conservative the algorithm will be.

Translation: min_child_weight is defined as the minimum leaf node sample weight sum (hessian). If the sum of sample weights in a leaf node produced by the tree partition step is less than min_child_weight, partitioning stops. In the linear regression model, the minimum number of instances reflects the minimum leaf node sample weight sum. The larger the min_child_weight, the more conservative the model will be, reducing model complexity and avoiding overfitting.

Next, we discuss the meaning of using hessian to represent node sample weights in tree models and linear models.

Do you remember the definition of the Hessian matrix? The hessian is the second derivative of the function value with respect to the variables. In the XGBoost algorithm, the Hessian is represented by the second derivative of the loss function with respect to the prediction value, as follows:

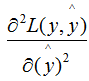
Where L represents the loss function, y and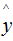 represent the true value and the predicted value, respectively.

2.1 Linear Regression Model

If the number of samples at a node is n, its loss function is:

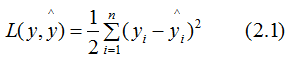
Taking the second derivative of (2.1):

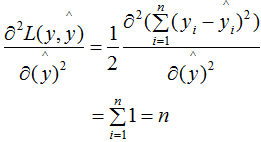
Thus, in the linear regression model, the number of samples at a node reflects the sample weight sum.

2.2 Tree Model

In the tree model, the sample weight is represented by the Hessian, and the condition for determining whether a node will split is to compare the sample weight sum of that node with min_child_weight; if greater, it will split; otherwise, it will not split (assuming other conditions for splitting are met).

To enhance understanding, this section uses binary classification logistic regression as an example:

The loss function for binary classification logistic regression is:

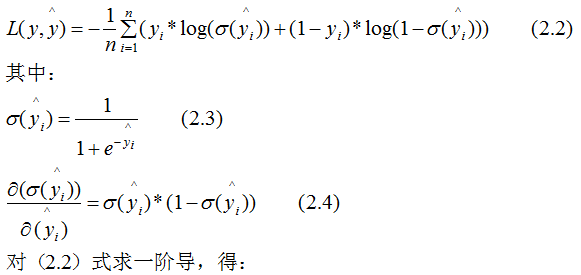
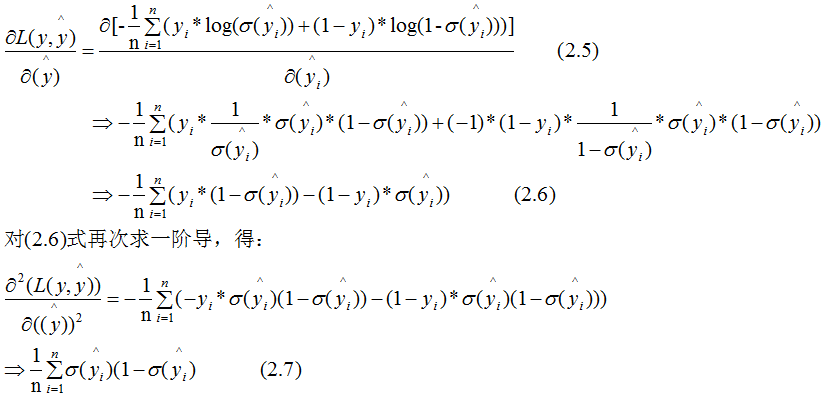
(2.7) represents the weight sum of all samples at a node, and we can qualitatively illustrate the relationship between (2.7) and min_child_weight:

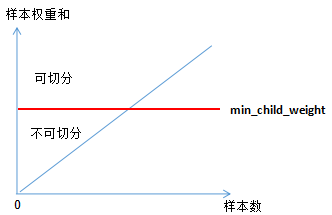
From the above figure, it can be seen that the number of samples is positively correlated with sample weight, thus the sample weight sum in the tree model reflects the number of samples to some extent.

From the properties of the XGBoost algorithm, we know:

(1) When yi is 1, the larger, the smaller the loss function, and (2.7) approaches 0.

(2) When yi is 0, the smaller, the smaller the loss function, and (2.7) approaches 0.

Thus, (2.7) can also represent the purity of a node; if the purity is greater than min_child_weight, the node can continue to split; if the purity is less than min_child_weight, it will not split.

Sort the second derivative values of the loss function, then split based on quantiles to choose the best split point. This will not be elaborated here; for specific algorithms, please refer toXGBoost Split Point Algorithm.

The XGBoost algorithm uses the second derivative of the loss function (Hessian) to represent sample weight. This idea reflects the number of samples at a node in the linear regression model and the purity of the node in the tree model.

Reference: https://stats.stackexchange.com/questions/317073/explanation-of-min-child-weight-in-xgboost-algorithm#

Good news!
The Beginner's Guide to Vision knowledge group is now open to the public👇👇👇





Download 1: OpenCV-Contrib Extension Module Chinese Version Tutorial
Reply "Extension Module Chinese Tutorial" in the WeChat public account backend to download the first OpenCV extension module tutorial in Chinese, covering installation of extension modules, SFM algorithms, stereo vision, object tracking, biological vision, super-resolution processing, and more than 20 chapters of content.

Download 2: Python Vision Practical Projects 52 Lectures
Reply "Python Vision Practical Projects" in the WeChat public account backend to download 31 practical vision projects including image segmentation, mask detection, lane line detection, vehicle counting, eyeliner addition, license plate recognition, character recognition, emotion detection, text content extraction, face recognition, etc., to help quickly learn computer vision.

Download 3: OpenCV Practical Projects 20 Lectures
Reply "OpenCV Practical Projects 20 Lectures" in the WeChat public account backend to download 20 practical projects based on OpenCV for advanced learning of OpenCV.

Group Chat

Welcome to join the WeChat group of public account readers to communicate with peers. Currently, there are WeChat groups for SLAM, 3D vision, sensors, autonomous driving, computational photography, detection, segmentation, recognition, medical imaging, GAN, algorithm competitions, etc. (which will gradually be subdivided in the future). Please scan the WeChat ID below to join the group, and note: "Nickname + School/Company + Research Direction", for example: "Zhang San + Shanghai Jiao Tong University + Vision SLAM". Please follow the format, otherwise, it will not be approved. After adding successfully, invitations will be sent to relevant WeChat groups based on research direction. Please do not send advertisements in the group, otherwise, you will be removed from the group. Thank you for your understanding~