New Intelligence Report
New Intelligence Report
Source: Reddit, Science
Editors: Daming, Pengfei
[New Intelligence Guide]Recently, Stanford University Chinese Professor Shanhui Fan’s team published an article in a sub-journal of Science, pointing out that whether it is sound waves, light waves, or other forms of waves, their descriptive equations can be equivalent to Recurrent Neural Networks (RNNs). This discovery may pave the way for the emergence of new types of simulation machine learning platforms. One of the authors also interacted with netizens on Reddit.Click the link on the right New Intelligence Mini Program to learn more!
Recently, the intersection between physics, mathematics, and machine learning has promoted the use of machine learning frameworks to optimize physical models, further facilitating researchers to develop many exciting new machine learning models (such as Neural ODEs, Hamiltonian Neural Networks, etc.) that draw on concepts from physics.
Researchers from Stanford University’s Shanhui Fan group are particularly interested in the idea that physics itself can be used as a computational engine. In other words, they are interested in physical systems that can serve as hardware accelerators or dedicated simulation processors for fast and efficient machine learning computations.

The corresponding author of this paper, Stanford University Professor Shanhui Fan
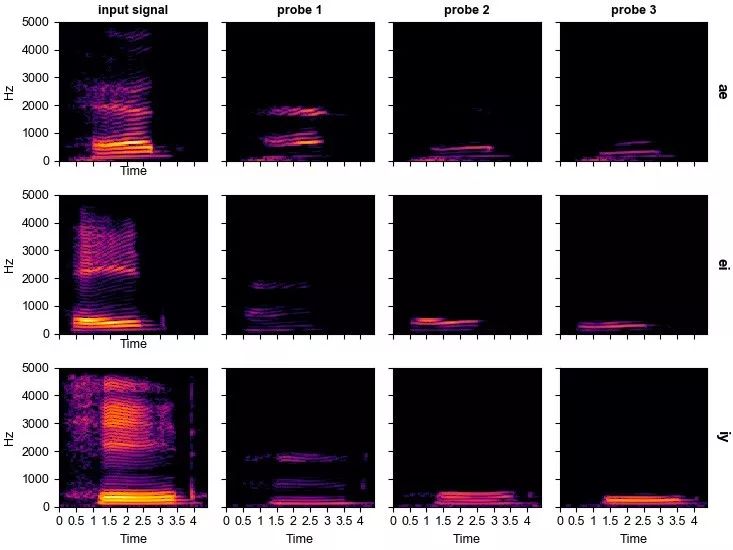
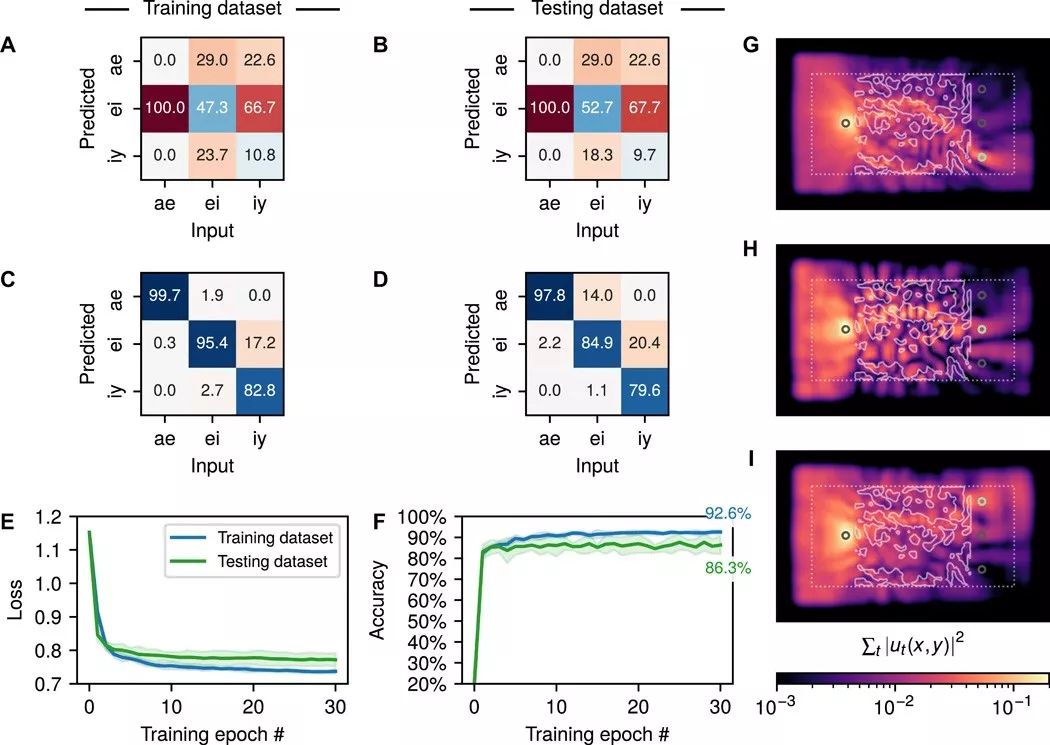
In their recent paper published in Science Advances, they demonstrated that the physical properties of waves can be directly mapped to the temporal dynamics of RNNs. Using this connection, researchers demonstrated that acoustic/optical systems (numerical models developed through PyTorch) can accurately classify vowels from recordings of human speakers. Essentially, this involves launching vowel waveforms into a physical model and allowing the optimizer to add and remove materials at 1000 points within the domain, effectively acting as the weights of the model.
Because this machine learning model corresponds to a physical system, it means that trained material distributions can be “printed” onto actual physical devices. The result will be similar to ASICs (Application-Specific Integrated Circuits) but used for specific RNN computations.
Researchers believe they indicate that, in addition to the energy carried by the pulse itself, it is also possible to perform complex recurrent machine learning computations completely passively, without energy consumption.
Paper Interpretation: Sound Waves, Light Waves Can Be Seen as Recurrent Neural Networks

Simulated machine learning hardware platforms are expected to be faster and more energy-efficient than digital platforms. Compared with digital models, sound waves and light waves in physics are natural choices for building analog processors for time-varying signals. This paper identifies the mapping between various forms of waves and computations in recurrent neural networks. This mapping indicates that standard training techniques for neural networks can be used to train physical wave systems, learning complex features in time data.
Inverse-designed inhomogeneous media can classify vowels from raw audio signals, achieving performance comparable to standard digital implementations of recurrent neural networks. These findings pave the way for new types of simulated machine learning platforms.
Equivalent Relationship Between Wave Dynamics and RNNs
RNNs convert an input sequence into an output sequence by applying the same basic operation to each member of the input sequence at each step of the input process. Memory of previous time steps is encoded as the hidden state of the RNN and updated at each step. The hidden state allows the RNN to retain past information and learn the temporal structure and long-term dependencies in the data. At a given time step t, the RNN operates on the current input vector xt of the sequence and the hidden state vector from the previous step ht-1 to generate the output vector yt and the updated hidden state vector ht.
Although RNNs have many forms of variants, a generally common implementation can be described by the following equations:
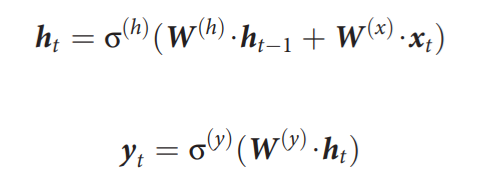
Similar to standard RNNs, the connection between the hidden state and the input and output of the wave dynamics equations is also defined by linear operators, which can be given as follows:
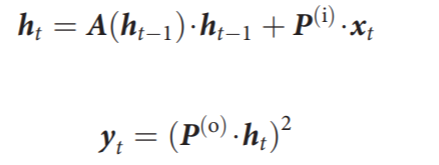
The input and output matrices define injection points and measurement points in the spatial domain. Unlike standard RNNs, the input and output matrices are dense, while the input and output matrices of the wave equation are sparse, as they are non-zero only at injection and measurement points, and these matrices do not change during training.
Conceptual Comparison Between RNNs and Wave Measurement Systems as Shown in Figure 1:
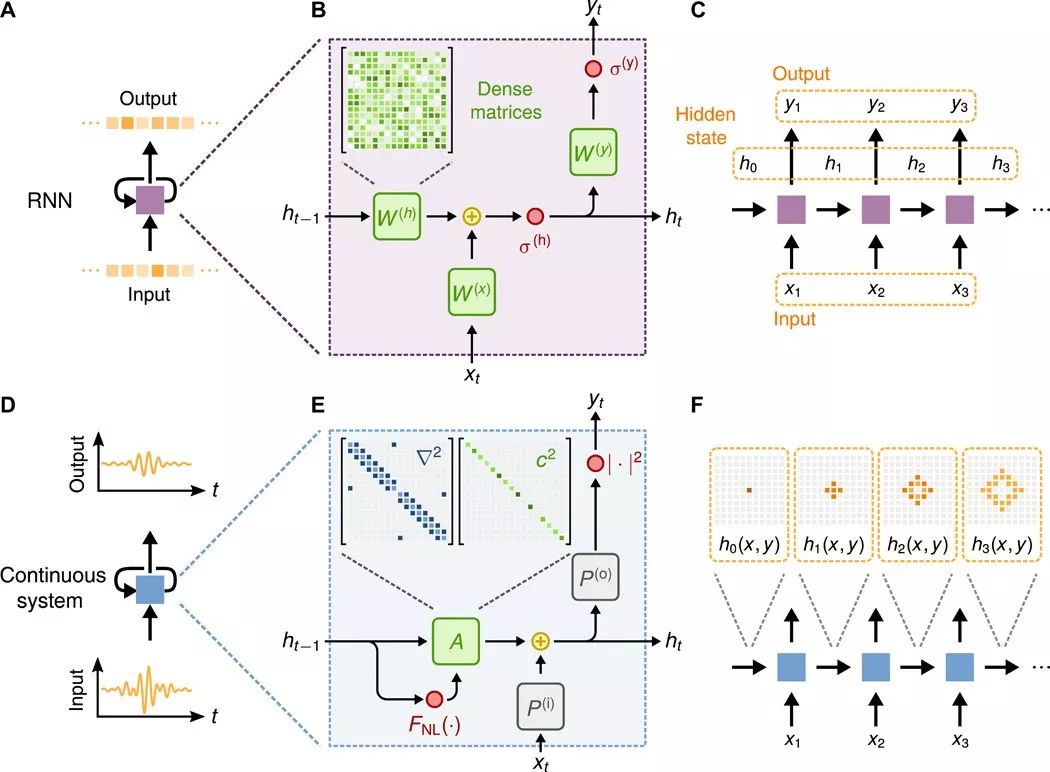
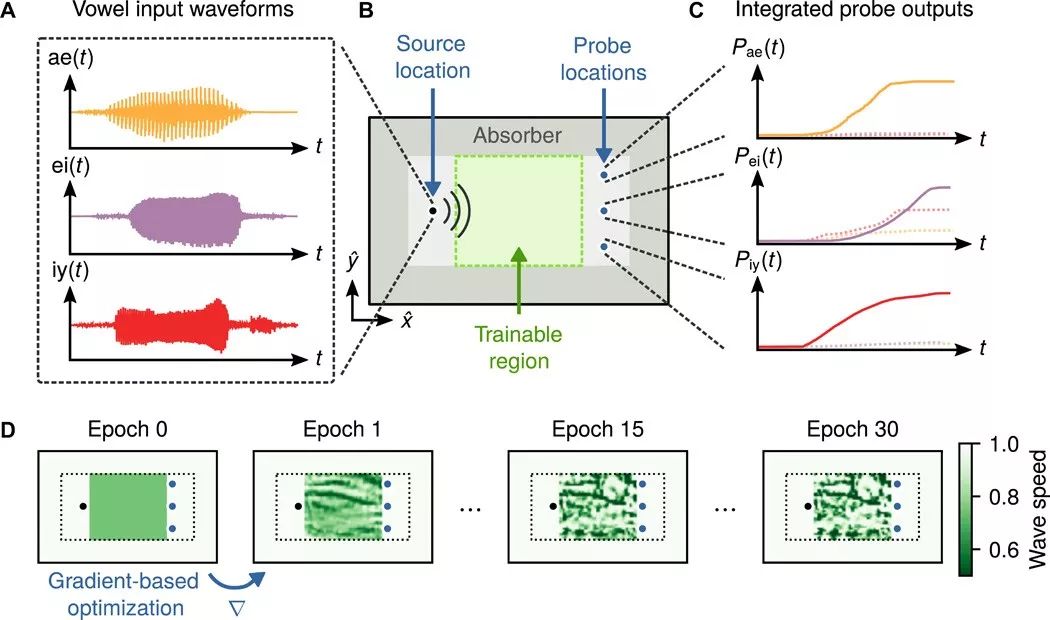
Future: Interconnection of Waves and RNN Concepts, New Platforms for Machine Learning Have Great Potential
The RNN based on wave principles introduced in this paper has many advantages, making it a promising successor for processing time-encoded information.
Moreover, unlike conventional RNNs, the wave equation enforces energy-saving constraints, preventing the norm of hidden states and output signals from growing indefinitely. In contrast, the unconstrained matrices defining the update relationships of standard RNNs can lead to vanishing and exploding gradients, which are significant issues to guard against when training traditional RNNs.
This paper proves that the wave dynamics equations can conceptually achieve equivalence with RNNs. This conceptual interconnection provides opportunities for the emergence of new types of simulated hardware platforms. This method of utilizing physics for computation may give rise to new platforms for simulated machine learning devices that have the potential to perform computational tasks more naturally and efficiently than their digital counterparts.

Reddit users showed great interest in this, but also had many questions about the research. The OP was very patient in answering.
Q: Is the nonlinearity in acoustics strong enough to make it more than just another glorious linear model?
A: In our scheme, the material response provides the hidden state non-linear activation function, while the detection circuit provides the output non-linearity. In acoustics, fluids present some interesting possibilities. For example, it is known that liquids with small bubbles have very strong non-linear acoustic responses. I believe these effects are easily encountered in medical ultrasound imaging. Typically, linear operations are still very expensive on digital processors, so having a very high-performance linear unit (e.g., in ONNs) still has a lot of value. Related to this, we also have another paper proposing activation functions for ONNs based on electro-optical circuits.
Q: Is the output created by actually playing somewhere and using a probe or speaker to measure the way sound propagates in the medium, or is it simulating a digital environment and using it to create different outputs?
A: Numerical simulation for demonstration. In the precise configuration of this paper, the microphone probe or receiver circuit also needs to perform some time integration of its recordings, as well as some additional comparison logic between time-integrated signals at different probes. However, most of the classification workload in the scheme has been transferred to the propagation and scattering of waves in the training medium.
Q: You talk a lot about physics, but this paper does not demonstrate the fundamental knowledge behind the physics of the phenomena being studied. I’ve completed online vowel recognition with 3-5 neuron MLPs (each vowel), so I know this is not difficult..
A: The focus is not to say that this specific task is too difficult for other models. Our work focuses on saying that wave-based physical systems can be compelling analog computing engines for recurrent machine learning (perhaps generally for computation).
Q: This is likely to encounter the “reality gap,” where training will utilize phenomena that exist in the physical model but do not exist or differ in reality. With so many self-interacting degrees of freedom (due to nonlinearity), even small discrete errors can produce surprising discrepancies with reality everywhere.
A: We operate in a simulation environment that (ideally) converges in terms of discretization error. This means that if we assume the simulation parameters (e.g., wave speed and non-linear material parameters) can reflect real-world values, then the simulation should represent the real situation well. We may want to improve constraints on the smallest feature sizes in the structure. We also need to consider three-dimensional effects (the demonstration in this paper is only two-dimensional). However, there should be no fundamental issues in solving these problems.
Q: Interesting research! Do you know what the upper limit of computational power such methods can reach?
A: That is definitely a good question, but it is difficult to provide a closed-form answer, which is something we are actively researching. The wave equation has some properties, such as causality and energy conservation, that we can expect will limit the forms of response that the system can produce.
Live Broadcast|New Intelligence Mini Program Technical Open Class Phase 1!
On the evening of January 6, author of the 16-volume Python series, Dong Fuguo, will reveal in the New Intelligence Mini Program “How to Write Python Code with ‘Python Flavor’?” There will also be opportunities for online interaction with industry experts to answer questions. Now scan the QR code below to grab a free reservation spot.

