Short-Term Traffic Speed Prediction Based on Spatio-Temporal Correlation Weighted LSTM

Liuyishi1, Guan Xuefeng1,2, Wu Huayi1,2, Cao Jun1, Zhang Na1

(1. Key Laboratory of Surveying and Mapping Remote Sensing Information Engineering, Wuhan University, Wuhan, Hubei 430079; 2. Collaborative Innovation Center of Geospatial Information Technology, Wuhan, Hubei 430079)

0 Introduction

In order to solve traffic problems such as road congestion and frequent accidents, with the popularity of vehicle GPS and the improvement of traffic sensor accuracy, traffic speed (referring to the speed of vehicles passing through a road segment) has gradually become one of the key focuses of current traffic prediction as a core element reflecting road traffic status. Since vehicle passing speeds fluctuate over time and across different road segments, accurately mining the characteristics of traffic speed in both time and space has become crucial for traffic speed prediction.

Traditional data-driven traffic prediction methods are mainly divided into two categories: statistical analysis-based prediction methods and general machine learning methods. Statistical analysis methods such as Kalman Filtering (KF) and Auto-Regressive Integrated Moving Average (ARIMA) heavily rely on prior knowledge and cannot effectively mine the information inherent in traffic data; general machine learning methods such as k-Nearest Neighbors (KNN) and Support Vector Regression (SVR) have enhanced information mining capabilities but lack deep feature extraction capabilities due to their single structural hierarchy. With the ability to obtain deep features, many deep learning models have begun to be applied to traffic speed prediction. For example, literature [7] proposed a method combining time series models and artificial neural networks (Time Series-Artificial Neural Network, TS-ANN) to model and predict real-time and historical speed data; literature [8] designed a short-term average speed prediction model based on Stacked Auto-Encoder (SAE) according to the spatio-temporal distribution characteristics of average road segment speeds; literature [9] combined Restricted Boltzmann Machines (RBM) with Recurrent Neural Networks (RNN) to predict taxi data in Ningbo; literature [10] constructed a speed-time matrix of roads and converted it into images for input into Convolutional Neural Networks (CNN) for feature learning; literature [11] used microwave detector data to learn long-term sequential dependency features of traffic speed sequences through Long Short-Term Memory Neural Networks (LSTM-NN); to capture the reverse dependency features of traffic data over time, literature [12] utilized Bi-directional LSTM for traffic speed prediction on a large-scale highway; literature [13] transformed the speed distribution map of the road network into a time-series grayscale image, combining CNN and LSTM models for speed prediction. Among these models, CNN can extract implicit spatial features, while LSTM can effectively learn long sequential patterns.

However, the above studies have not effectively correlated and quantified the temporal and spatial features for traffic speed prediction. The spatial features of road segment traffic speed are usually represented by spatial adjacency relationships or graph structures, while temporal features can be further divided into two types: the historical dependency features of the segment itself and the temporal similarity features of speed changes between segments. Taking traffic congestion as an example, when a certain road segment experiences congestion, surrounding segments may also experience corresponding delays; when congestion disappears, the speeds of adjacent segments will gradually increase, indicating a certain similarity and lag in the change patterns between the two. This correlation information of speed sequences manifests spatially as the topological adjacency relationships of segments and temporally as the similarity correlation of speed changes, significantly influencing traffic speed variations. To fully reflect this correlation information, we need to consider both spatial and temporal features comprehensively and provide a quantification method to distinguish the importance of different correlation information to enhance the effectiveness of traffic speed prediction.

To input the spatio-temporal correlation features into the model, this paper first designs a spatio-temporal correlation degree to quantify the correlation degree between speed sequences from both temporal and spatial dimensions, and processes it by weighting the speed sequences. Based on this, this paper proposes a spatio-temporal correlation weighted LSTM model (STC-LSTM) for traffic speed prediction. The model first defines a temporal correlation degree through Summation Dynamic Time Warping (SDTW); then combines it with the adjacency relationships of road segments to form a spatio-temporal correlation degree to comprehensively describe the spatio-temporal features of the correlation degree between segments; finally, this spatio-temporal correlation degree is used as weights in conjunction with LSTM for traffic speed prediction.

1 Temporal Correlation Degree Based on SDTW

The temporal correlation degree is a measure used to determine the closeness of two given speed sequence variation curves, essentially a measure of similarity. In similarity measures for time series, commonly used distance functions include Euclidean Distance (ED), Mahalanobis Distance (MD), and Cosine Distance (CD). For univariate sequences with consistent sampling intervals and equal lengths, Euclidean Distance is generally used as the similarity measure. Given two speed time series X={x1,x2,⋯,xn} and Y={y1,y2,⋯,yn}, where X and Y are vectors, the distance DED(X,Y) is:

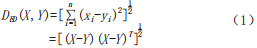
Commonly used time series similarity distance measurement methods include Discrete Fourier Transform (DFT) based on ED, Discrete Wavelet Transform (DWT) based on ED, and Dynamic Time Warping (DTW). The Discrete Fourier Transform and Discrete Wavelet Transform decompose sequence signals in the frequency domain and compute distances between different components, which can help with noise reduction and classification; Dynamic Time Warping aligns time scales by considering numerical similarities, effectively addressing issues such as time axis offsets and scale distortions. Since traffic flow consists of dispersed vehicles, its speed variations occur through transmission, which requires time; thus, the influence of speed variations between segments has a certain lag characteristic, and similar sequences may exhibit offset phenomena. Considering this, we choose to use the Dynamic Time Warping method. However, since Dynamic Time Warping only considers numerical characteristics when solving time axis offsets, it cannot effectively address offsets on the numerical axis. This can lead to situations where a point from one sequence maps to a large portion of another sequence, incorrectly calculating similarity distances, leading to the “singularity problem.” To solve the singularity problem, it is necessary to introduce gradient features in the time dimension based on Dynamic Time Warping, thereby reducing the situation where a point maps to continuous areas. A more effective method is SDTW.

SDTW first defines the feature value Fs(x(i)) containing both numerical features and gradient features as:

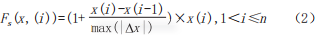
Where, x(i) represents the i-th value in the sequence X={x1,x2,…,xn}, max(|∆x|) represents the maximum value of x(i)-x(i-1) in sequence X, which indicates the maximum gradient of speed values, where the difference of adjacent points represents the gradient of a certain point, such as using x(i)-x(i-1) to represent the gradient of x(i). The role of max(|∆x|) is to constrain the sizes of gradients within [-1,1], thus incorporating gradient information into features in a ratio format. The ratio of numerical features is 1, which is greater than that of gradient features, playing a larger role in building features, while gradient information plays a supporting role. Therefore, feature Fs is not overly sensitive to small deviations in numerical values. Combining with formula (1), we can obtain the local distance d(i,j) from the i-th value in sequence X to the j-th value in sequence Y as:

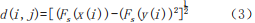
From the n×n local distances d, a distance matrix D can be constructed. Thus, under the constraints of boundary conditions, continuity, and monotonicity, we can obtain the regularized distance SDTW(x,y) between sequences X and Y as:

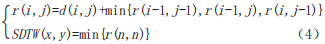
Where, r(i,j) is the cumulative distance of local distances along the path from (0,0) to (i,j) in the distance matrix D. According to continuity and monotonicity constraints, a point can only be reached from (i-1,j-1), (i-1,j) or (i,j-1), min{r(i-1,j-1),r(i-1,j),r(i,j-1)} indicates the point with the minimum cumulative distance among the three as the starting point. Based on the above, the similarity distance between any two road segment speed sequences can be calculated, forming the SDTW distance matrix.

Define the temporal correlation degree T between two road segment speed sequences XY as:

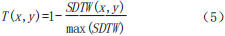
Where, max(SDTW) is the maximum value in the SDTW distance matrix. After normalization, the range of temporal correlation degree T is [0,1], with each segment’s temporal correlation degree with itself being 1, and the temporal correlation degree of two segments with the farthest SDTW distance being 0. The lower the similarity between the speed sequences of two segments, the larger their SDTW distance and the smaller the temporal correlation degree; the greater the similarity, the smaller the SDTW distance and the larger the temporal correlation degree.

2 Spatio-Temporal Correlation Degree Combined with Spatial Adjacency Relationships

Considering the direction of traffic flow on road segments, urban traffic networks are generally abstracted as directed graphs. However, unlike ordinary directed graphs, for first-order adjacency relationships, the influence of traffic states between upstream and downstream is bidirectional. When a road segment is clear, the influence mainly transmits from upstream to downstream segments; when a road segment is congested, the traffic of downstream segments will affect the traffic state of upstream segments. Therefore, we can obtain the first-order adjacency matrix S of the road network:

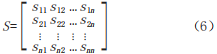
Where, g represents the adjacency relationship between segments. However, the traffic flow relationships between road networks are not limited to first-order adjacency relationships. For example, although segment a and segment b are adjacent, they do not have an upstream-downstream relationship. The traffic flow from segment a and segment b flows to downstream segment c; when the traffic flow of segment a increases, it will inevitably cause an increase in the flow of segment c, resulting in traffic delays, while the delay phenomenon of segment c will also affect upstream segment b, causing the vehicle speed of segment b to slow down correspondingly. The traffic flow between segment a and segment b is not directly related; their influence occurs indirectly through segment c, thus viewing them as second-order adjacency relationships.

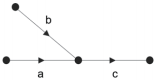
Figure 1 Influence of Road Traffic Statuses

Figure 1 Influence of Road Traffic Statuses

The second-order adjacency relationship can be described as the first-order adjacency matrix of the first-order adjacency, and so on. By iterating, we can obtain the k-th order adjacency relationship of road segments. Based on this, the adjacency matrix G of the entire road network containing n road segments is defined as:

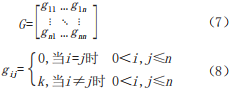
Where, i and j represent any two road segments in the network, and k represents the order of adjacency relationship between road segment i and a different road segment j. The closer the adjacency relationship between two segments, the smaller g; the farther the adjacency relationship, the larger g.

Based on spatial adjacency relationships and temporal correlation degrees, we define the spatio-temporal correlation degree wij between two segments as:

Where, using the form 1/(g+1) ensures that the value range is in (0,1], which not only ensures that the fraction is meaningful (the denominator is greater than 0), but also guarantees that the spatio-temporal correlation degree is positively correlated with the correlation degree between road segments. Using the natural constant as the base for exponentiation can elevate the temporal and spatial features of spatio-temporal correlation degree on the vertical axis, expanding the differences and enhancing the expression of spatio-temporal features, which is beneficial for the next step of weighting. Ultimately, the spatio-temporal correlation degree matrix Wx can be obtained, where a larger spatio-temporal correlation degree w indicates a greater correlation of speed time series data between segments.

3 LSTM Model Based on Spatio-Temporal Correlation Weighting

This paper proposes a Long Short-Term Memory (LSTM) model based on spatio-temporal correlation weighting (STC-LSTM), which includes a spatio-temporal correlation weighting part, an LSTM layer, and a fully connected layer. The specific structure is shown in Figure 2.

Figure 2 Weighted LSTM Model Based on Spatio-Temporal Correlation

Figure 2 Weighted LSTM Model Based on Spatio-Temporal Correlation

The model’s input consists of the historical speed data of n road segments for m time periods prior to time t, and the model’s output is the predicted speed value of segment x at time t+1. To improve prediction accuracy, the model integrates temporal and spatial features into the weight matrix, predicting by weighting the input speeds. This retains the correlation information of speed variations between segments and further emphasizes the speed sequences of segments that are more closely related to the predicted segment, enhancing the learning ability regarding the spatial adjacency relationships and speed variation similarity features.

The weight matrix Wx in the figure is the spatio-temporal correlation degree matrix mentioned above. When the number of input segments is n, the matrix size is n×n, representing the weights of speed values in each segment’s speed sequences, which are multiplied by the corresponding speed values in the speed sequences and then summed, thus completing the weighting process of the spatio-temporal correlation degree matrix Wx. The historical speed data inputted through the spatio-temporal correlation degree matrix Wx can yield m weighted speed sequences, denoted as S={st–m+1,st–m+2,…,st}.

Where, wxi is the spatio-temporal correlation degree between the predicted segment x and the current segment i, and vi is the speed value at time i. As indicated by the spatio-temporal correlation degree formula, the spatio-temporal correlation degree between the segment to be predicted and itself is always the largest, ensuring a positive correlation between the weighted speed sequence size and the degree of correlation. The processing of input data as the object of feature extraction in the prediction model directly affects the selection of features and the accuracy of prediction results. This weighting method reflects the different degrees of correlation between speed sequences by altering the predicted input speed values, emphasizing the speed sequences that are more closely related to the predicted segment.

Subsequently, these t weighted speed sequences are input into each LSTM unit for prediction. The hidden state Ht outputted by the LSTM layer is processed through a fully connected layer, and the final predicted speed 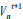can be calculated using the weight matrix W2 and the bias b2, with the activation function being Tanh.

4 Experiments and Analysis

4.1 Experimental Data and Model Parameters

The experimental data in this paper consists of trajectory data from 2,330 taxis in Wuhan City over a 30-day period in June 2014, with text fields including taxi ID, sampling time, latitude and longitude, instantaneous speed, travel direction, etc., with a sampling frequency of approximately every 40 seconds, totaling 91 million trajectory records. First, the trajectory data underwent preprocessing, including outlier cleaning, segmentation, and road network matching, then segments with relatively high coverage of trajectory points were selected to form a sub-region of the road network for the study area, which contains a total of 34 segments, as shown in Figure 3 (blue and red segments).

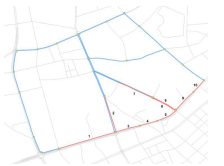
Figure 3 Road Network Structure of Study Area

Figure 3 Road Network Structure of Study Area

From the study area, we selected segments numbered 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 (red segments) as predicted segments, while the 34 segments in the study area served as input segments, providing correlation sequence information for the predicted segments, which were input into the model for prediction.

The traffic speed of a segment is the average speed of road traffic flow; thus, we need to process the instantaneous speed. Based on the sampling frequency and actual distribution of the trajectory data, we employed a 20-minute time interval, resulting in a length of 2,160 for the speed sequence of each segment (3×24×30). After categorizing all trajectory points by segment and time period, the mean of all instantaneous speeds of trajectory points for each segment within each time period was calculated as the observed speed value for the segment.

The prediction task of the experiment is to use the historical speed data of the input segments for the first 12 time periods (each time period being 20 minutes) to predict the speed of the predicted segments for the next time period. 80% of the data samples were used as the training dataset, and 20% as the testing dataset. For each segment, the first 1,728 speed values were used for training data, and the last 432 speed values were used for testing data. The three-dimensional tensor input of the model , where N_S is the number of historical speed data for the input segments (1,728), N_T is the number of historical time periods (12), and N_R is the number of input segments (34).

The experiment utilized Stochastic Gradient Descent (SGD) as the model optimizer, with a learning rate and decay value set to 0.001 and 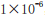respectively. The loss function used was Mean Squared Error (MSE). During training, the batch size was set to 128, and the epochs were set to 500. The number of LSTM neurons was initialized to 40, and the number of neurons in the output fully connected layer was set to 1, with the activation function chosen as tanh, totaling 41 parameters, with a total of 7,360 parameters.

4.2 Experimental Results and Analysis

The experiment employed three metrics to evaluate the model’s prediction accuracy on the test set, namely Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), and Root Mean Square Error (RMSE), with their calculation formulas as follows (where Y is the model output value, and is the true value):

The prediction results of the STC-LSTM model compared to the ARIMA model, SVR model, and LSTM model are shown in Table 1.

Table 1 Model Prediction Results

Table 1 Model Prediction Results

From the speed prediction results in Table 1, it can be seen that the prediction accuracy of the model varies significantly across different road segments, with the average percentage error as low as 8% and as high as 29%. This variation is due to the different traffic change patterns of each segment, which may exhibit certain spatial heterogeneity, leading to different prediction effects for different segments.

However, overall, the prediction results of the STC-LSTM model show an average MAPE better than other models. The average MAPE of the STC-LSTM model is 15.76%, with an average MAE of 1.2136 km/h, compared to the LSTM model, which shows a reduction of 1.07% in average MAPE and a reduction of 0.054 km/h in average MAE. This indicates that the spatio-temporal correlation weighting approach is effective in speed prediction, reflecting the spatio-temporal characteristics of speed variations between road segments to some extent.

Nonetheless, the root mean square error of the LSTM model based on spatio-temporal correlation weighting fluctuates between 1.17 and 2.02, indicating that the predicted speeds have a certain bias. Taking segments 1, 2, and 3 as examples, combined with Figures 4, 5, and 6, it can be seen that the predicted speed values can reflect the general trend of speed variations, but the actual speed fluctuates significantly and frequently. This aspect is challenging for the proposed model to simulate. One reason may be that the recorded true values contain errors or anomalies, failing to adequately reflect the actual driving conditions; another reason is a common issue with most prediction models, where high-frequency fluctuations exhibit strong randomness, making them difficult to simulate through learning.

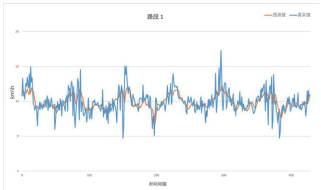
Figure 4 Comparison of Prediction Value and Observed Value for Road 1

Figure 4 Comparison of Prediction Value and Observed Value for Road 1

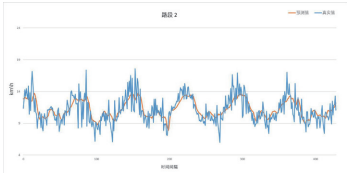
Figure 5 Comparison of Prediction Value and Observed Value for Road 2

Figure 5 Comparison of Prediction Value and Observed Value for Road 2

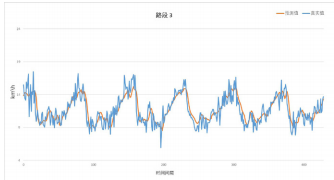
Figure 6 Comparison of Prediction Value and Observed Value for Road 3

Figure 6 Comparison of Prediction Value and Observed Value for Road 3

To further explore the impact of correlation degree measurement methods on prediction accuracy, the temporal correlation degree and spatial adjacency relationships were weighted separately and compared with the overall weighting method (ST) of spatio-temporal correlation degree. The STC-LSTM model is the original prediction model that comprehensively considers spatial and temporal correlation degrees; the SC-LSTM model (Spatio Correlation Long Short-Term Memory) is a prediction model that only considers spatial correlation degree, with a different calculation method for correlation degree w than the original model; the TC-LSTM model (Temporal Correlation Long Short-Term Memory) is a prediction model that only considers temporal correlation degree. The prediction results of the three models are shown in Table 2.

Table 2 Prediction Results of Roads with Different Spatio-Temporal Patterns of Speeds

Table 2 Prediction Results of Roads with Different Spatio-Temporal Patterns of Speeds

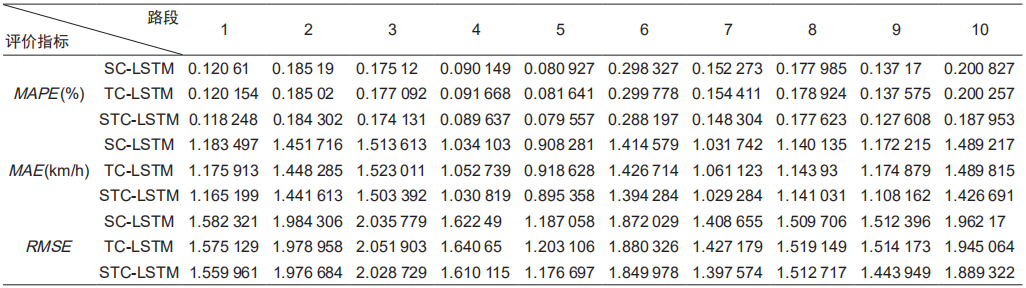
In Table 2, taking MAPE as an example, among all predicted segments, the average MAPE of STC-LSTM is 0.157556, while the average MAPE of SC-LSTM and TC-LSTM are 0.1618578 and 0.162652, respectively, and the average MAPE of unweighted LSTM from Table 1 is 0.1683369. It can be observed that the overall weighting of spatio-temporal correlation degree yields better prediction accuracy than the individual weighting methods of temporal correlation degree and spatial adjacency relationships, while both temporal correlation degree weighting and spatial adjacency relationship weighting outperform the unweighted LSTM. The conclusion is similar when comparing segment by segment. This indicates that both temporal correlation degree and spatial adjacency relationships can enhance predictions, with a more significant improvement when both are combined.

5 Conclusion

Traffic speed varies significantly over time and across different road segments. For the problem of traffic speed prediction, this paper constructs an LSTM model based on spatio-temporal correlation weighting. The model explores the variation characteristics of traffic speed in time and space, quantifying the correlation features of speed variations in spatio-temporal dimensions using spatio-temporal correlation degree, and fully utilizes the LSTM model’s ability to learn long-term dependency patterns, achieving traffic speed prediction. Compared to ordinary Long Short-Term Memory network models, the LSTM model based on spatio-temporal correlation weighting achieves a significant improvement in accuracy, proving the model’s effectiveness.

The traffic speed prediction model designed in this paper still has room for further research and improvement. On one hand, the sampling frequency of the data itself limits the prediction results, resulting in significant differences in model prediction accuracy across different segments; on the other hand, the model’s division of correlation features in spatio-temporal dimensions has some overlap, which requires further exploration.

This Issue Review