As we all know, LLMs are powerful, but their ability to perform complex reasoning is still not strong enough.
For example, on the GSM8K dataset, Mistral-7B can only achieve an accuracy of 36.5% even with techniques like Chain of Thought (CoT). Although fine-tuning can effectively enhance reasoning capabilities, most LLMs rely on fine-tuning data that has been distilled from more powerful models like GPT-4, or may have originally been synthesized from these powerful models.
At the same time, researchers are actively developing a more challenging method that can provide assistance: using a superior teacher LLM to enhance reasoning capabilities.
To improve reasoning capabilities without a superior model, a promising paradigm is to leverage the knowledge within the LLM itself. For example, a method called RAP adopts a self-exploratory solution that iteratively improves the reasoning performance of LLMs through self-reward feedback. Unfortunately, research shows that this paradigm has two fundamental problems.
First, when performing reasoning, LLMs often struggle to effectively explore the answer space. This self-exploratory approach often gets stuck in an answer space due to poor quality of reasoning steps, even after multiple attempts.
Second, even if self-exploration finds high-quality reasoning steps, small language models (SLMs) struggle to discern which reasoning steps are of higher quality and to determine if the final answer is correct, making it difficult to effectively guide self-exploration. Research shows that results guided by basic conventional rewards from self-exploration are not better than random guessing.
Moreover, SLMs are more prone to the above two problems because they are less capable. For example, GPT-4 can optimize its output through self-optimization, but SLMs find it challenging to do so, which may even lead to a decrease in output quality. This severely hinders the promotion and application of neural language models.
To address these issues, a research team from Microsoft Research Asia and Harvard University proposed Self-play muTuAl Reasoning, abbreviated as rStar. In simple terms, this method is akin to having two average students check each other’s answers on an exam, ultimately improving their scores to even match that of top students. The team claims that rStar “can enhance the reasoning ability of SLMs without fine-tuning or superior models.”

Paper Title:
Mutual Reasoning Makes Smaller LLMs Stronger Problem-Solvers
Paper Address:
https://arxiv.org/pdf/2408.06195
Code Link:
https://github.com/zhentingqi/rStar (to be released)
Method
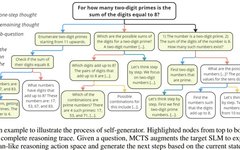
To solve the above challenges, rStar divides the reasoning process into answer generation and mutual verification, as shown in Figure 2.
To address the first challenge, the team introduced a set of rich human-like reasoning actions to thoroughly explore various reasoning task spaces.
For the second challenge, they designed a reward function specifically for SLMs that evaluates intermediate steps, thus avoiding reliance on their often unreliable self-assessment.
Additionally, the team used another SLM as a discriminator to enhance the MCTS process, mutually verifying the correctness of each trajectory with the discriminator SLM.
Using MCTS Rollout to Generate Reasoning Trajectories
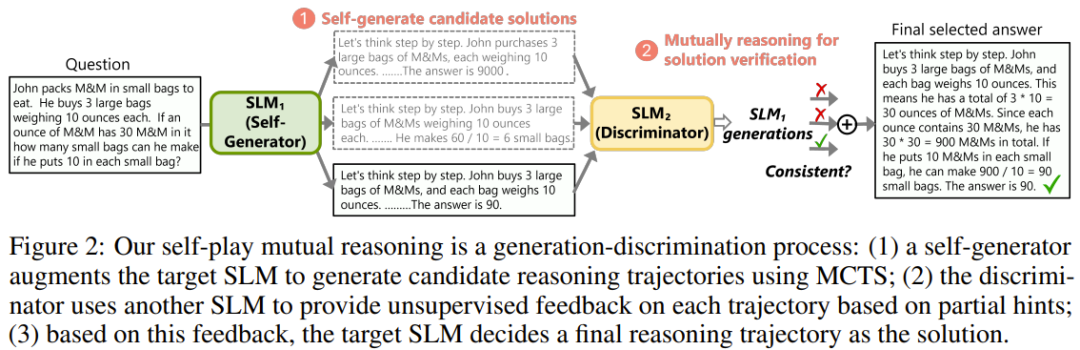
A set of rich human-like reasoning actions. The core of MCTS generation lies in the action space, which defines the scope of tree exploration. Most MCTS-based methods use a single action type when constructing the tree. For example, the action in RAP is to propose the next sub-question, while the actions in AlphaMath and MindStar are to generate the next reasoning step. However, relying on a single action type may lead to poor exploration of the space.
To address this issue, the team reviewed how humans perform reasoning. Different people solve problems in different ways: some break the problem down into sub-problems, others solve it directly, and some rephrase the problem from a different perspective. Moreover, people adjust their methods based on the current state and choose different actions as needed.
Inspired by the human reasoning process, the team constructed a more diverse dataset containing five types of actions to maximize the potential of SLMs to correctly solve complex reasoning problems.
Action 1: Propose a step of reasoning. For a given problem, this action allows the LLM to generate the next step of reasoning based on existing reasoning steps.
Action 2: Propose the remaining reasoning steps. This action, like standard CoT, can achieve “fast thinking” to solve simple problems that require few steps. Given the already generated reasoning steps, it allows the LLM to directly generate the remaining steps until reaching the final answer.
Action 3: Propose the next sub-question and its answer.
Action 4: Answer this sub-question again. Considering that action 3 might not correctly answer the corresponding sub-question, this action serves to answer it again.
Action 5: Rephrase the problem/sub-question. This new action reformulates the problem in a simpler way. Specifically, it asks the LLM to clearly list all conditions in the problem statement.
The above five actions define a highly diverse action space {A1, A2, A3, A4, A5}.
At each step i, MCTS selects an action a_i from this space. Then, based on the current state (i.e., the previously generated trajectory x ⊕ s_1 ⊕ s_2 ⊕ … ⊕ s_{i−1}), it uses action a_i to generate the next reasoning step s_i. Note that some actions need to be executed in sequence. Figure 3 provides an example.
As shown in Table 1, each action plays an important role in improving the final reasoning accuracy.

-
Reward Function
Another key component of MCTS is the reward function, which evaluates the value of each action and provides guidance for tree expansion. For SLMs, the team designed a simple yet effective reward function. Their method is inspired by AlphaGo, scoring each intermediate node based on its contribution to the final correct answer. This way, actions that frequently yield correct answers receive higher rewards, making them more likely to be selected in future MCTS tree expansions.
Here, the reward value of a node s generated after executing action a is defined as Q (s, a). Initially, all unexplored nodes are assigned Q (s_i, a_i) = 0, enabling random tree expansion. Upon reaching the first terminal node n_d, a reward score Q (s_d, a_d) is calculated based on whether it yields the correct answer.
Then, along the trajectory t = x ⊕ s_1 ⊕ s_2 ⊕ … ⊕ s_d, this score is backpropagated to each intermediate node. Specifically, for each s_i, its Q value is updated as follows: Q (s_i, a_i) = Q (s_i, a_i) + Q (s_d, a_d). The reward value used to calculate the Q (s_d, a_d) at the terminal node is the likelihood (confidence) of a self-consistent majority vote.
-
Using MCTS Rollout to Generate Answers
The following describes how MCTS generates candidate reasoning trajectories. Starting from the initial root node s_0, various searches are performed, including selection, expansion, simulation, and backpropagation. Specifically, the simulation uses the default Rollout strategy. To obtain more accurate reward estimates, the team performs multiple Rollouts. To balance exploration and exploitation, they use the well-known UCT (Upper Confidence bounds for Trees) to select each node. The mathematical form of this selection process is:
where N (s, a) is the number of times node s has been visited in previous iterations, and N_parent (s) represents the number of visits to the parent node of s. Q (s, a) is the estimated reward value, which will be updated during the backpropagation process. c is a constant that balances exploration and exploitation.
Once the search reaches a terminal node (which may be a terminal state or may have reached a predefined maximum tree depth d), a trajectory from root to terminal node is obtained. All trajectories iteratively obtained from Rollout are collected as candidate answers. Next, they need to be verified.
Using Mutual Consistency to Select Reasoning Trajectories
Based on all collected trajectories, the team proposed using reasoning mutual consistency to select answers.
-
Achieving Reasoning Mutual Consistency through a Discriminator SLM
As shown in Figure 2, in addition to the target SLM, the team also introduced a discriminator SLM, which provides external unsupervised feedback for each candidate trajectory.
Specifically, for t = x ⊕ s_1 ⊕ s_2 ⊕ … ⊕ s_d, the reasoning steps starting from a randomly sampled step i are masked. The previous reasoning trajectory t = x ⊕ s_1 ⊕ s_2 ⊕ … ⊕ s_{i-1} is then provided as a prompt to the discriminator SLM to complete the remaining steps. Since the previous i-1 reasoning steps are used as a prompt, the difficulty is reduced, making it more likely for the discriminator SLM to provide the correct answer.
Figure 4 compares whether the answer completed by the discriminator SLM matches the original trajectory t. If they match, t is considered a validated trajectory that can be ultimately selected.

The final trajectory is selected by the target SLM. After applying reasoning mutual consistency to all candidate trajectories, the target SLM is then asked to select the final trajectory from the validated ones. To calculate the final score for each trajectory, the team multiplies its reward by the confidence score obtained through Rollout at its terminal node. The trajectory with the highest final score is selected as the answer.
Experiments
Experimental Setup
rStar is applicable to various LLMs and reasoning tasks. The team evaluated five SLMs: Phi3-mini, LLaMA2-7B, Mistral-7B, LLaMA3-8B, and LLaMA3-8B-Instruct.
The reasoning tasks tested include five, among which four are mathematical tasks (GSM8K, GSM-Hard, MATH, SVAMP) and one is a common sense task (StrategyQA).
For experimental details, please refer to the original paper.
Main Results
The team first evaluated the effectiveness of rStar on general reasoning benchmarks. Table 2 compares the accuracy of rStar and other current best methods on different SLMs and reasoning datasets. To demonstrate the effectiveness of the new generator, the team also provided the accuracy of rStar (generator @maj), which achieved accuracy by validating answers solely through majority voting without using the discriminator.
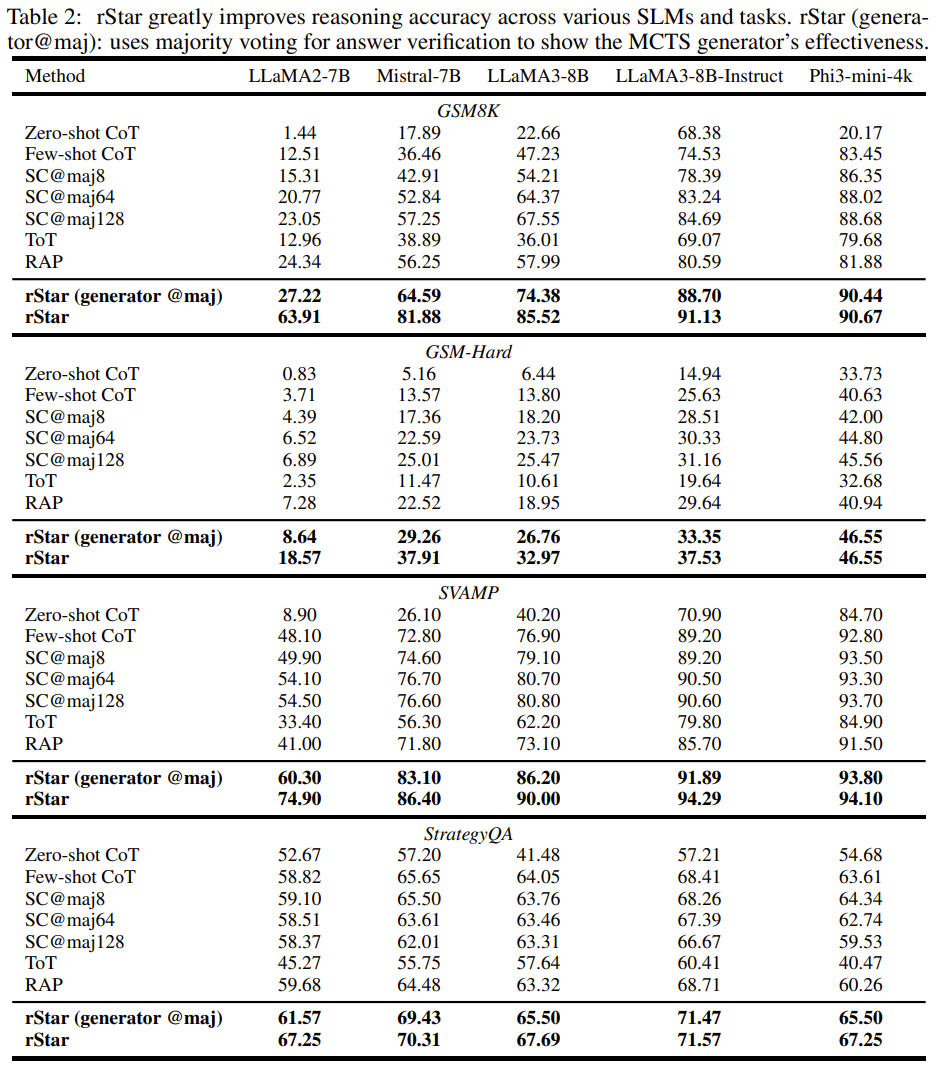
The team pointed out three key results:
1. SLMs aided by rStar have stronger problem-solving capabilities. For example, on the GSM8K dataset, the accuracy of LLaMA2-7B with few-shot CoT is only 12.51%. However, with the assistance of rStar, its accuracy improved to 63.91%, a result close to that obtained through fine-tuning, as shown in Figure 1. Similarly, the performance of Mistral with rStar even surpassed that of the fine-tuned MetaMath by 4.18%. This improvement indicates that SLMs already possess strong reasoning capabilities but need guidance to generate and select correct answers.
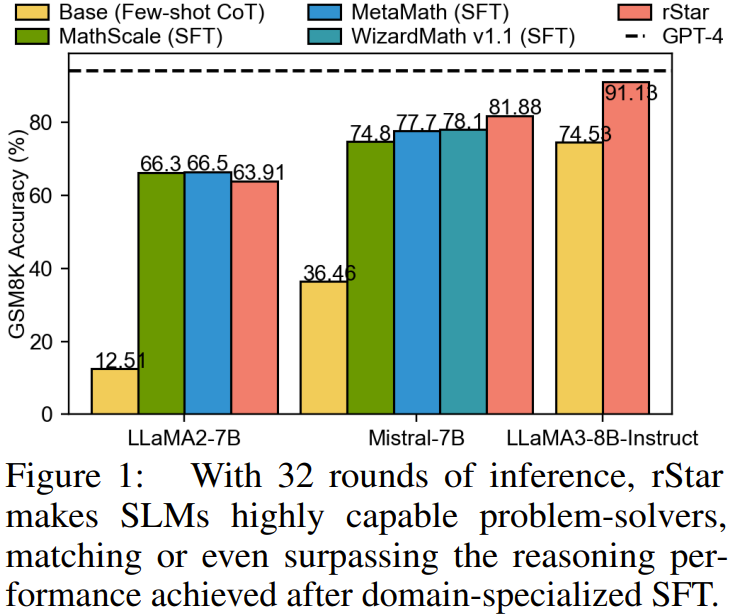
2. rStar can consistently elevate the reasoning accuracy of various assessed SLMs across different tasks to the current best levels. In contrast, other comparative methods fail to achieve stable excellent performance across all four benchmarks. For instance, while SC (self-consistency) excels in three mathematical tasks, it fails to effectively solve the logical reasoning task of StrategyQA.
3. Even without the newly proposed discriminator for validating reasoning trajectories, the newly proposed MCTS generator still performs well in enhancing the reasoning accuracy of SLMs. For example, on the GSM8K dataset, the accuracy of rStar (generator @maj) is 2.88%-16.39% higher than RAP, 10.60%-38.37% higher than ToT, and 1.69%-7.34% higher than SC.
-
Results on High-Difficulty Mathematical Datasets
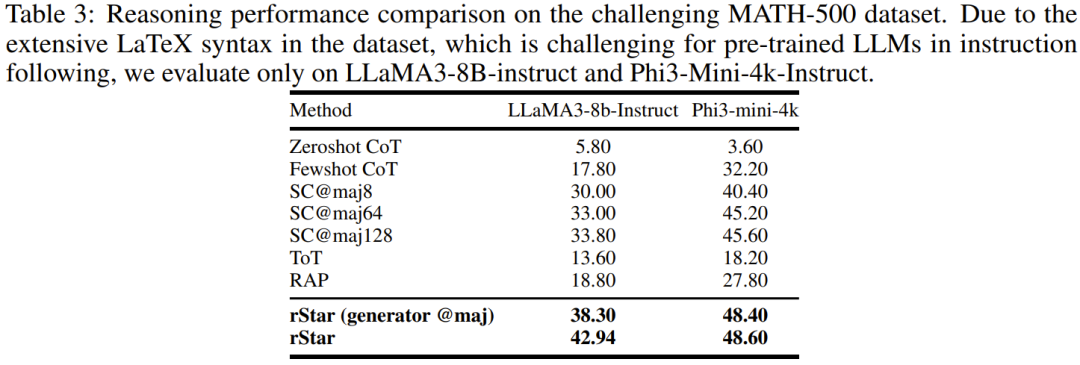
The team also evaluated rStar on a more challenging mathematical dataset. They chose the GSM-Hard and MATH datasets for this purpose. Following the convention of similar studies, they used MATH-500, a subset of representative problems from the MATH dataset, to speed up the evaluation. As shown in Tables 2 and 3, rStar can significantly improve the reasoning accuracy of SLMs on these high-difficulty mathematical datasets.
Ablation Study
-
Effectiveness of Different Rollouts
rStar uses a Rollout strategy to perform MCTS tree expansion. More Rollouts generate more candidate answer trajectories but also raise reasoning costs. Figure 5 compares the accuracy of SC, RAP, and rStar using different Rollouts on GSM8K.
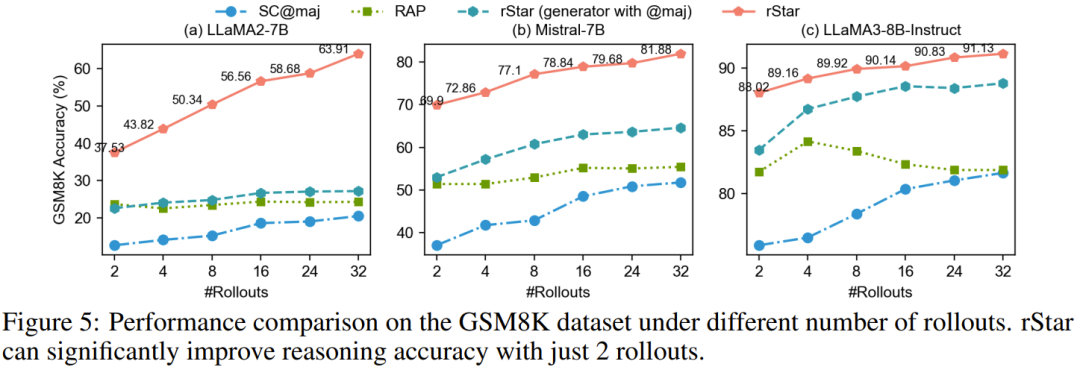
Two key observations were made:
1. Even with just 2 Rollouts, rStar can significantly enhance the reasoning accuracy of SLMs, demonstrating its effectiveness;
2. More Rollouts benefit both rStar and SC, while RAP often saturates or even declines after 4 Rollouts. One reason is that RAP’s single-type action space limits the effectiveness of MCTS exploration.
-
Effectiveness of MCTS Generator
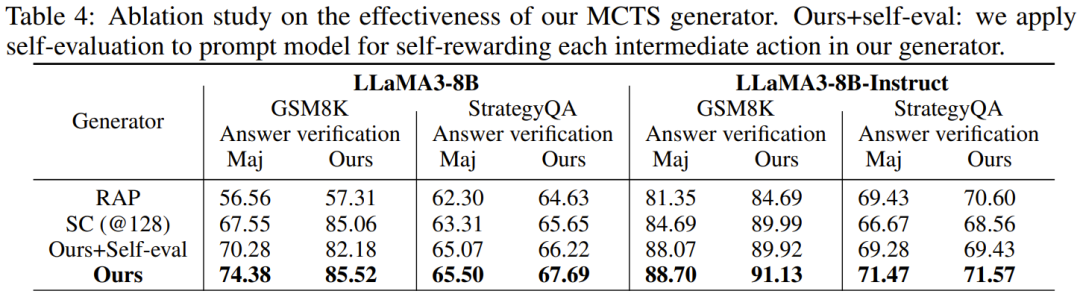
The team compared the MCTS generator’s performance with that of three other generators. As shown in Table 4, the newly proposed MCTS generator outperformed the other generators comprehensively. Additionally, the effectiveness of the reward function adjusted for SLMs was also demonstrated, as self-assessment would lower the accuracy of the new generator.
-
Effectiveness of the Discriminator
The team set up two evaluation experiments.
The first experiment compared the discriminator method with majority voting and self-verification methods. The results are shown in Table 5 (left), where the advantages of the discriminator method are quite evident.

The second experiment examined the impact of different discriminator models. The results are shown in Table 5 (right), indicating that selecting different discriminator models typically does not affect the effectiveness of the reasoning mutual consistency method in verifying answers. Notably, even using a powerful GPT-4 as a discriminator, the performance only slightly improved (from 91.13% to 92.57%). This suggests that the reasoning mutual consistency method can effectively use SLMs to verify answers.

Scan the QR code to add the assistant WeChat
About Us